18 KiB
05 | 密码学:为什么说区块链站在了巨人肩膀上?
你好,我是自游。
在数字社会的今天,我们的工作生活离不开密码学,可以说离开密码学,我们就像是在网络世界中裸奔,毫无隐私可言。然而普通大众可能对密码学知之甚少,它就像是一位低调的守护者,默默维护着网络世界的安全。
区块链中也大量使用了密码学算法,前面课程里我们就多次提到过。比如哈希算法以及区块链存储中讲过的交易签名,它们都属于密码学算法。那今天这一讲,我就为你详细讲讲区块链中常用到的密码学算法。
密码学与区块链
在深入密码学算法的学习之前,我想先为你理清密码学与区块链的关系。中本聪在比特币白皮书中开篇就说,比特币是基于密码学构建的去信任数字货币。我认为他把密码学与区块链的关系说得很清楚,密码学是因,区块链是果。
怎么理解他们之间的这种因果关系呢?可能有的同学会认为是区块链需要有可追溯,不可篡改等特性,所以中本聪才设计了几种密码学算法去支撑他的构想。但这是完全错误的,属于颠倒黑白的想法。
密码学是先于区块链产生的基础学科,有完备的理论及技术体系。是中本聪及其先行者们在理解及运用密码学的过程中,看到了基于密码学创造数字货币的可能性。正因为哈希算法有校验数据完备性的能力,中本聪才会想到利用区块哈希前后关联形成区块链;也是因为数字签名有证明所有权的能力,所以才会基于数字签名去证明数字货币所有权问题。
基于以上的分析,我想你已经明白区块链之所以有独特的性质,是因为密码学中的某些算法已经有了这些性质的雏形,只不过是区块链是将这些算法加以揉和,最终以一个整体呈现给我们。
理清楚了密码学与区块链是什么关系,我们再来说说区块链中的密码学,区块链用到的密码学算法有很多,且不同的区块链使用的算法也有所差异。
但总的来说,你只需要理解两类基本算法就可以,那就是哈希算法以及非对称加密算法,而且学习密码学跟学习其他技术不太一样,理解密码学原理需要深厚的数学功底。
其实工程师完全可以把密码学当作黑盒,你不需要太关注其技术原理,而只需要理解它的特性以及应用场景就可以了。
哈希算法
我们先一起看看之前提及比较多的哈希算法,哈希算法又称散列函数,它可以将任意长度的数据转换成短的、固定长度的数据指纹。
其实哈希算法不是只有一个固定的实现,而是一类算法的统称,比如常用的有MD5跟SHA-256。要评判一个哈希算法是否足够优秀,我们有4个标准:正向快速、逆向困难、输入敏感和避免碰撞。
正向快速
什么是正向快速呢?这点很好理解,如果给定信息和算法规则,可以在有限的时间内计算得到信息的哈希结果。你说你设计了一个优秀的哈希算法,结果一次计算过程就花了好几秒,那只能说你的设计不够优秀,虽然时间有限,但根本没办法在真实场景中使用。
为了能给你更直观的感受,我专门写了一个程序,测试我们常用到的MD5跟SHA-256这两个哈希算法的计算到底有多快。
package main
import (
"crypto/md5"
"crypto/sha256"
"fmt"
"sync/atomic"
"time"
)
func main() {
data := []byte("极客时间") // 明文数据
// 两个计数
md5Count := int64(0)
sha256Count := int64(0)
go func() {
for {
md5.Sum(data) // MD5哈希计算
atomic.AddInt64(&md5Count, 1) // 原子计数+1
}
}()
go func() {
for {
sha256.Sum256(data) // SHA-256哈希计算
atomic.AddInt64(&sha256Count, 1) // 原子计数+1
}
}()
time.Sleep(time.Second) // 等待1秒
// 输出结果
fmt.Printf("md5 count: %d\n", md5Count)
fmt.Printf("sha256 count: %d\n", sha256Count)
}
// 计算结果
// md5 count: 10064932
// sha256 count: 5727246
可以看到,最终得到的结果是非常给力的,在大概1秒钟的时间内,MD5计算了1000万次,而SHA-256算法也计算了500万次。
我这里仅仅是用了一台普通的电脑,如果是在服务器上跑,相信结果会更震撼。通过这个测试,相信你对正向快速这个标准的解读应该足够清晰了。当然单纯分析哈希算法的计算速度是没有意义的,还是要将其带入到具体的业务场景中,此处只是给你一个直观的印象。
逆向困难
接下来我们看第二个标准,那就是如果给定哈希结果,在有限的时间内基本不可能逆推出原始信息。也就是说一个优秀的哈希算法是不可能通过密文反推明文的,这也就是不可逆的根源。
我们来举个例子:
# echo "极客时间" | md5sum
e0aac893629b048e8797800294f55004
这是我在电脑的命令行中执行的一条命令,得到了“极客时间”的MD5哈希值。
想象一下,如果我不告诉你e0aac893629b048e8797800294f55004是“极客时间”的MD5哈希结果,你能通过这段字符,反推出它代表的明文是“极客时间”吗?
不光你懵,我想计算机看到这问题也会懵,因为计算机只能通过穷举去猜结果。
当然,并不是说哈希算法就是不能够被破解的。相反,MD5哈希可以说已经被变相破解了,既然逆向困难,那我提前穷举常见的数据组合存起来,有破解需求的时候我再回头查就好了,简单而又粗暴。
我通过cmd5.com查了一下“极客时间”的哈希值,发现还未被收录,说明暂时还是安全的。但现已不推荐使用MD5,区块链中通常使用的是SHA-256,它的安全性较高。
输入敏感
我们再看另一个标准,就是原始信息即使发生一丁点的变化,重新计算的哈希值与之前比较都应该有很大的不同。
这个标准主要是降低原始信息被部分推断的风险。如果新产生的哈希值与之前的相差不大,计算机就可以利用差异去推断变化,相比穷举,困难度当然是降低了,而这却是不被允许的。
还是来看一个例子:
# echo "极客时间 " | md5sum
a9dad13b05a8ee28df851dbcb87f3a3b
我通过在“极客时间”后面多加了一个空格,得到的哈希值跟上一个例子中的结果对比,肉眼可见有很大不同。你也可以自己在电脑上试一试,看看结果是否一致。
避免碰撞
你可能就会有疑问,以MD5算法为例,任意数据信息经过哈希算法后都可以得到32位哈希值,那不会重复吗,毕竟32位哈希值能表现的数据量是比较少的?
其实你只说对了一半,32位在计算机中是用128位二进制数表示的值,所以实质上MD5哈希能表示的数据有$2^{128}$个那么多,你如果去算一算就会发现,这其实是一个很大的数字。如果你仍然认为不够保险,那还有更高位数的算法可以选择,比如SHA-256及SHA-512等。
当然,表示的数据量大,并不代表着就不会有两个不同的数据得到相同的哈希值,这确实在实践中已经出现过。所以,在设计哈希算法时,应该避免不同的明文信息产生相同的哈希值。
区块链中的哈希
现在我们了解了优秀哈希算法评判的4个标准,相信你对哈希算法的特性已经有所认识了。那区块链中是怎样应用哈希算法的呢?我们接着往下说。
因为哈希算法相当于是对信息提取摘要,是数据的指纹,因此经常被用于数据完整性的校验,而区块链在此基础上又做了适当的延伸。
区块链中用到哈希算法的地方主要是交易哈希和块哈希,主要功能就是校验交易及区块的完整性,以及充当区块链网络中交易及区块的唯一标识。说到这里,你有没有想到上一讲我留下的第二个讨论题?
没错,在区块链数据落盘的时候,我们就可以使用交易哈希、区块哈希分别作为交易及区块的数据主键,只要保持了数据与标识对应索引关系,就可以把交易跟区块存储在任意数据库中。
区块哈希还有另一个作用,区块属性中包含了前一个区块的哈希,从而构建成一条由区块哈希关联的数据链条,所以我们称区块链为哈希链也不为过。利用哈希算法对输入的敏感性,作恶者如想篡改区块链数据,必须从被修改处开始依次修改后续的全部区块,哈希算法的加入增加了作恶者篡改的成本,可以说是哈希算法成就了区块链单节点的不可篡改特性。
非对称加密算法
讲完哈希算法的内容,我们再将目光转向非对称加密算法。说到非对称,肯定有与之对应的对称加密算法。
顾名思义,对称与非对称体现在对密钥的处理上。对称表示加密和解密都使用同一套密钥。而非对称加密却不一样,分为公钥跟私钥,如果使用公钥加密,只有用对应的私钥才能解密,反之亦然。那既然有了对称加密算法,为什么还要发明非对称加密算法呢?
这里我用一个快递的例子帮你解惑。你在外地打拼,给远在老家的父母寄了一份珍贵的礼物,用一个精美的盒子做包装。为了礼物不被破坏,其实最好的方法就是你亲自送回家,但这不现实,你只好发快递。
而父母收到你的礼物非常高兴,他们立马也快递给你一些老家的土特产,用的正是你送礼物的那个盒子。就这样来来回回好几轮,原来精美的盒子已经变得残破不堪,甚至可以透过盒子看到内部的物品,也很容易丢失。
这个例子让我们形象地理解了对称加密的不足。其中礼物跟土特产就是需要交换的信息,而那个起初精美的盒子就是密钥。
对称加密算法要想保证密钥不被泄露,最好的办法是面对面协商,而且即便是面对面协商了密钥,后续也不能多次使用,否则使用次数越多,泄密风险越高,且不能保证中途没有其他人篡改。
还是用快递的例子,为了能保证快递物品不丢失,这次过年回家你给父母买了个快递保险箱,共两把钥匙,父母一把,你留一把。这样后续再寄快递时,就可以把物品放在保险箱中,这样就算用快递运输,也不用怕物品被调包了,因为除了你跟父母之外,没有人可以再打开保险箱。
这里的保险箱就相当于公钥,而钥匙就相当于私钥。这个“保险箱”方案,其实在密码学里就对应着非对称加密算法的思想。
非对称加密算法的密钥是一对,分为公钥跟私钥。公钥可以随便公开,而私钥需要私密保存,而只要私钥不被泄露,信息交换过程就是安全的。当然这个例子还是与非对称加密有所差异,真正的私钥应该只有一份。
非对称加密算法虽然解决了对称加密算法使用过程中遇到的问题,但其加解密的效率是远不如对称加密算法的。因此,在使用过程中常采用混用的方式,即明文数据采用对称加密算法进行加密,然后使用非对称加密算法加密对称加密的密钥和明文数据哈希,对方收到信息后,用匹配成对的另一个密钥解密数据并核对明文数据哈希,混用的方式可很好的平衡安全性与时效性。
非对称加密算法跟哈希算法一样,也是一类算法的统称。现用的比较多的是RSA跟ECC椭圆曲线加密算法,RSA多用于互联网信息传输中,比如我们上网用到的https通信,而在区块链中基本都使用的是ECC类的变种,比如ECDSA跟ED25519等。相较于RSA,ECC密钥较短,在拥有更高安全性的同时还有更好的性能。
非对称加密算法的原理较为复杂,其推导过程是严密的数学推理,此处不再展开,你如果感兴趣,可以参考扩展阅读中的内容。
区块链中的非对称加密
了解了算法的特性,我们再回过头来看区块链中是如何使用非对称加密算法的。你如果之前了解过区块链,就会发现在区块链中,好像并没有哪个地方使用非对称加密对数据进行加解密。的确,区块链中对非对称加密算法的使用并不是直接被用作数据加密,而是利用其具备身份确权的能力,也就是数字签名。
什么是数字签名?顾名思义,其实跟我们平常手写签名的概念及作用是一样的,都是用于证明你的身份,且对所签署的文件或者数据进行确认授权。
在诸如比特币以太坊等公有链中都有类似于地址、账户的概念,我们可以认为这就是区块链中的身份证,这个身份证不同于现实中需要政府统一颁发,而是分散的基于非对称加密算法的公钥的一种形变表示。
这里可以引申一个小知识点,你通过数字货币手机钱包创建了一个账户,此时区块链网络并不知道,只有当你接收到一笔转账之后,网络中才有你这个账户的信息。
那如何确认这个账户是属于你的呢?道理非常简单,只要你能证明你可以花费账户中的余额就可以了,而这证明的关键就在于数字签名。既然账户是公钥的形变表示,那么必定存在与之对应的私钥,且只存在你的手中。
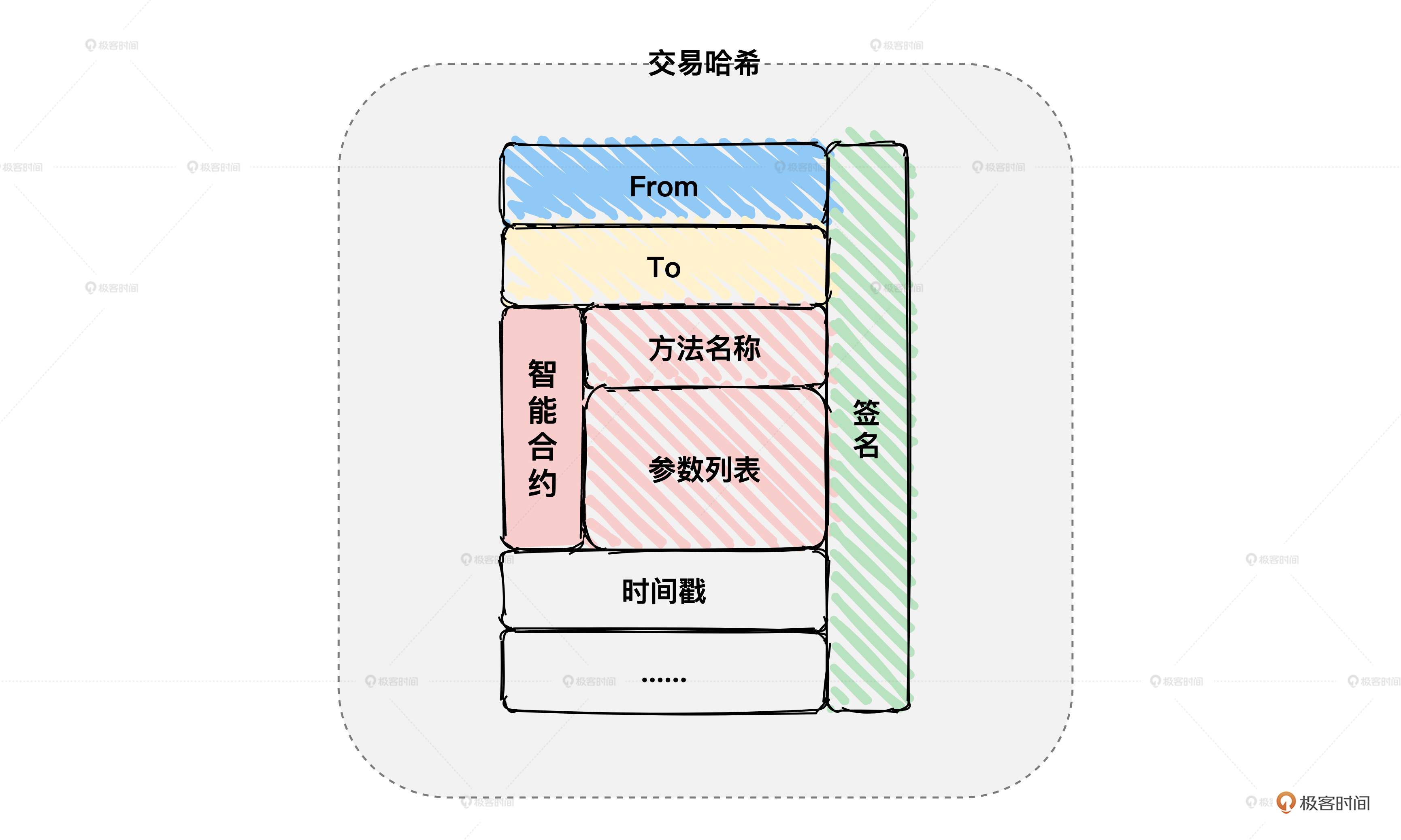
那数字签名到底是怎样的原理呢?我结合上一讲交易结构中的交易签名来给你讲一讲。
我们可以将交易结构分成两部分,左边部分是交易的基本属性,而右边只包括签名。
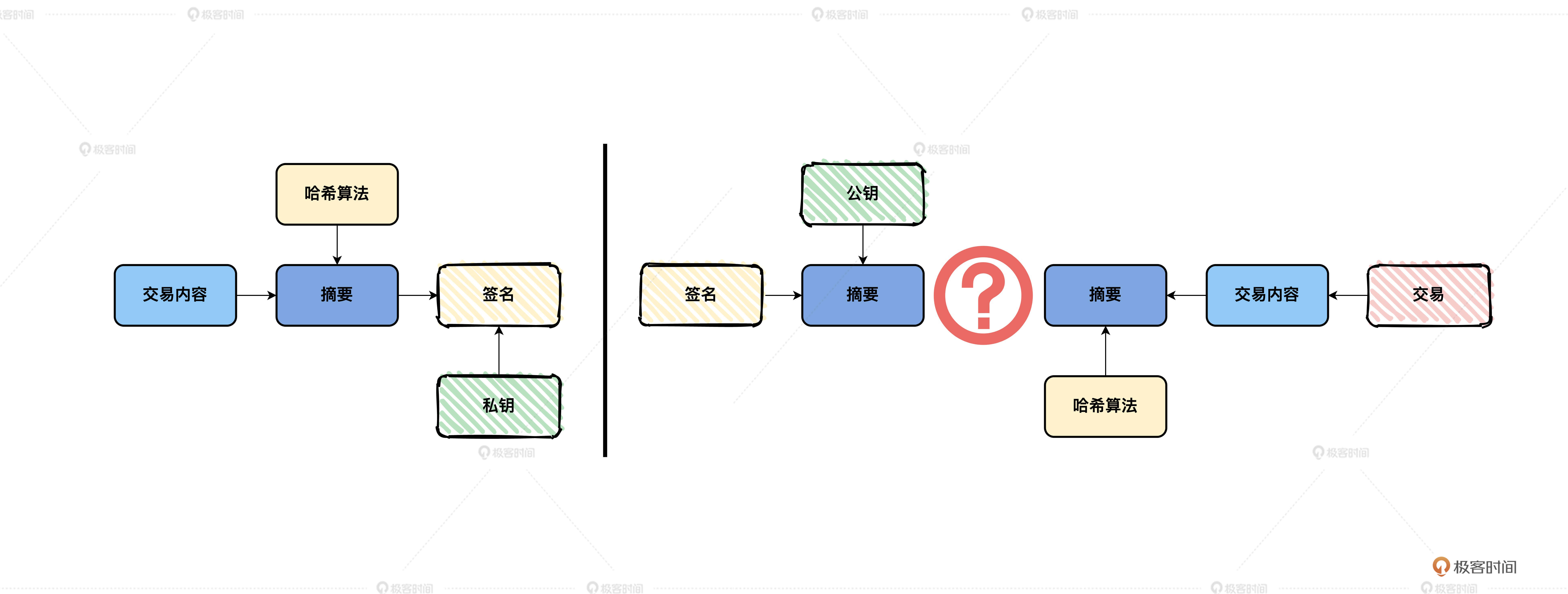
如果我们不看签名,其实左边部分已经能够基本表示交易的内容了,只是缺少了证明。因此我们将左边部分看作一个整体,然后对它进行哈希计算得到交易摘要,接着用你手中的私钥对交易摘要进行加密,而加密的结果就是交易的签名。
而如果要验证交易,只需要按照相反的流程进行就可以了,将交易签名使用对应的公钥解密得到签名中包含交易摘要,同时将明文的交易内容利用哈希算法再计算交易摘要,然后将签名中的交易摘要与自主计算的交易摘要进行对比,如果匹配,则表示交易验证成功。
数字签名的本质也是一种加密,只不过针对的是数据的哈希摘要,并不是数据本身。这么做有什么好处呢?主要有两点,一方面证明了确实是你自己构建的这笔交易,因为其他人没有你的私钥,无法假冒。另一方面,因为数字签名是有哈希算法参与的,因此也继承了哈希算法的特性,能保障交易的完整性,确保了交易不会被他人无故篡改。
总结
这一讲我从哈希算法跟非对称加密算法为出发点,为你浅析了区块链中常用到的密码学算法。
哈希算法被用来抽象交易哈希跟区块哈希,除了用于保证数据完整性外,还能用来构建由区块哈希关联的哈希链条,增加作恶篡改的成本。
区块链中使用非对称加密算法并不是直接用于数据加密,而是主要用作交易签名,数字签名集成了哈希算法与非对称加密算法的双重特性,在保证交易完整性的同时,还能证明交易发起者的身份。
区块链中并不是只用到了哈希跟非对称加密,几乎所有的区块链都在此基础上做了些许的衍生,比如追求隐私交易的ZCash就引入了密码学中的零知识证明,专注于隐私计算的区块链就引入了同态加密等等。
密码学的知识浩如烟海,现在区块链用到的只是冰山一角。通过今天的学习我们可以发现,正因为有了密码学的加持,区块链就好像站在了巨人的肩膀上。
讨论
- 你通过数字货币手机钱包创建了一个账户,此时区块链网络并不知道,只有当你接收到一笔转账之后,网络中才有你这个账户的信息。你知道这是为什么吗?
- 如果说数字签名是公钥对信息摘要加密而产生的,结果会怎么样?还会有现在这种效果吗?
扩展阅读
- 对于密码学整体发展的历史,你可以参考密码学初探。
- 这一讲重点讲解了区块链中最常见、最基础的密码学算法,想了解更多关于区块链中涉及的密码学的门类,可以阅读V神列的知识清单。
- 如果你看得还不过瘾,想了解文中介绍的密码学算法原理,可以参考这几篇文章:哈希算法原理,RSA加密算法原理以及ECC椭圆曲线加密算法介绍。
欢迎你在留言区跟我互动,主动思考、积极交流会让你更有收获。如果这一讲对你有帮助,也欢迎你分享给自己的朋友、同事。
我是自游,我们下一讲再见。