421 lines
21 KiB
Markdown
421 lines
21 KiB
Markdown
# 03 | 矩阵:为什么说矩阵是线性方程组的另一种表达?
|
||
|
||
你好,我是朱维刚。欢迎你继续跟我学习线性代数,今天我们要讲的内容是“矩阵”。
|
||
|
||
在开始学习之前,我想先问你个问题,你觉得,学习矩阵有什么用呢?你可以先自己想一想。之后我们讲任何一个知识的时候,你都可以从这个角度出发,自己先思考一下,这样有助于你对所学内容理解得更深刻。
|
||
|
||
对于刚才那个问题,我的答案很简单,就一句话,从我们程序员的角度去理解的话,**矩阵可以极大地提高计算机的运算效率**。怎么说呢?我给你举一个例子。在机器学习中(特别是深度学习,或者更具体一点,神经网络),并行计算是非常昂贵的。
|
||
|
||
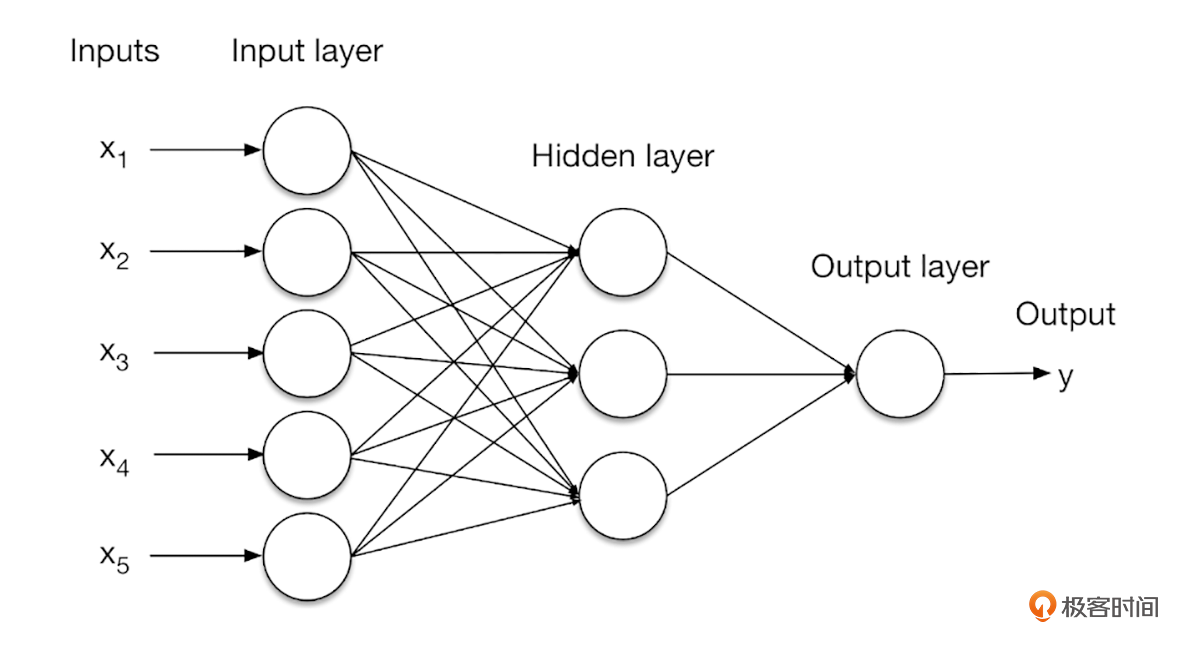
|
||
|
||
上图是一个典型的神经网络架构,在这时候,矩阵就能发挥用武之地了,计算$H$隐藏层输出的公式是:$H = f( W.x + b )$,其中$W$是权重矩阵,$f$是激活函数,$b$是偏差,$x$是输入层矩阵。而这个计算过程就叫做**向量化**(Vectorization),这也是GPU在深度学习中非常重要的原因,因为GPU非常擅长做类似矩阵乘之类的运算。
|
||
|
||
$$
|
||
X=\\left|\\begin{array}{l}
|
||
x\_{1} \\\\\\
|
||
x\_{2}
|
||
\\end{array}\\right|
|
||
$$
|
||
|
||
$$
|
||
W=\\left|\\begin{array}{ll}
|
||
w\_{1} & w\_{2} \\\\\\
|
||
w\_{4} & w\_{5} \\\\\\
|
||
x\_{3} & w\_{6}
|
||
\\end{array}\\right|
|
||
$$
|
||
|
||
$$
|
||
H=f\\left(\\left|\\begin{array}{ll}
|
||
w\_{1} & w\_{2} \\\\\\
|
||
w\_{4} & w\_{5} \\\\\\
|
||
x\_{3} & w\_{6}
|
||
\\end{array}\\right|\\left|\\begin{array}{l}
|
||
x\_{1} \\\\\\
|
||
x\_{2}
|
||
\\end{array}\\right|+b\\right)
|
||
$$
|
||
|
||
不过,矩阵也不仅仅局限于神经网络的应用,同时它也可以用在计算机图形图像的应用中,比如,三维物体从取景到屏幕的显示,就需要经历一系列的空间变换,才能生成二维图像显示在显示器上。在这个计算过程中,我们都需要用到矩阵。
|
||
|
||
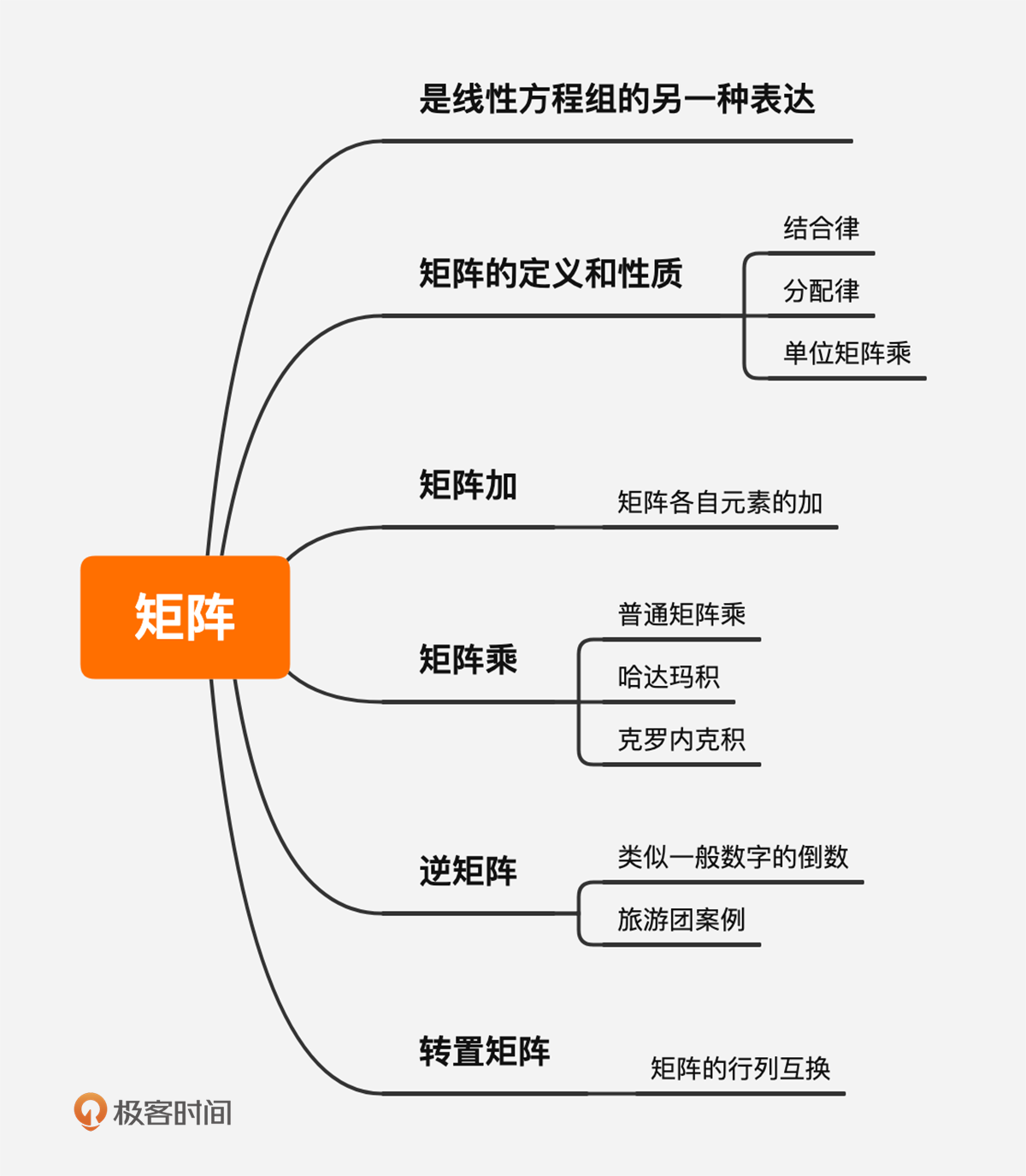
矩阵是非常实用的,但它正式作为数学中的研究对象出现,其实是在行列式的研究发展起来之后。英国数学家 Arthur Cayley 被公认为矩阵论的创立人,他提出的矩阵概念可能来自于行列式。但我相信另一种说法,提出矩阵是为了更简单地表达线性方程组,也就是说,矩阵是线性方程组的另一种表达。
|
||
|
||
## 矩阵的基本概念
|
||
|
||
线性方程组的概念很简单,上节我们已经简单提过。你在小学或中学肯定也学过二元一次方程和二元一次方程组。
|
||
|
||
$$ax+by=c$$
|
||
|
||
$$
|
||
\\left\\{\\begin{array}{l}
|
||
a\_{1} x+b\_{1} y+C\_{1}=0 \\\\\\
|
||
a\_{2} x+b\_{2} y+C\_{2}=0
|
||
\\end{array}\\right.
|
||
$$
|
||
|
||
在这样一个方程组中,$a1$、$a2$、$b1$、$b2$不能同时为0。当我们把二元一次方程组再扩展一下,变成多元一次方程组时,我们就能得到线性方程组的一般表达,即$AX=B$。
|
||
|
||
$$
|
||
\\left\\{\\begin{array}{l}
|
||
a\_{11} x\_{1}+a\_{12} x\_{2}+\\cdots+a\_{1 n} x\_{n}=b\_{1} \\\\\\
|
||
a\_{21} x\_{1}+a\_{22} x\_{2}+\\cdots+a\_{2 n} x\_{n}=b\_{2} \\\\\\
|
||
\\cdots \\cdots \\cdots \\cdots \\cdots \\cdots \\cdots \\cdots \\cdots \\cdots \\\\\\
|
||
a\_{m 1} x\_{1}+a\_{m 2} x\_{2}+\\cdots+a\_{m n} x\_{n}=b\_{m}
|
||
\\end{array}\\right.
|
||
$$
|
||
|
||
于是,这个线性方程组的所有系数就构成了一个$m×n$的$m$行$n$列矩阵:
|
||
|
||
$$
|
||
A=\\left\[\\begin{array}{cccc}
|
||
a\_{11} & a\_{12} & \\ldots & a\_{1 n} \\\\\\
|
||
a\_{21} & a\_{22} & \\ldots & a\_{2 n} \\\\\\
|
||
\\ldots & \\ldots & \\ldots & \\ldots \\\\\\
|
||
a\_{m 1} & a\_{m 2} & \\ldots & a\_{m n}
|
||
\\end{array}\\right\]
|
||
$$
|
||
|
||
我们把$A$称为该方程组的系数矩阵,而当我们把等式右边的常数$b$放入矩阵后,就是下面这样:
|
||
|
||
$$
|
||
\\widetilde{A}=\\left\[\\begin{array}{ccccc}
|
||
a\_{11} & a\_{12} & \\ldots & a\_{1 n} & b\_{1} \\\\\\
|
||
a\_{21} & a\_{22} & \\ldots & a\_{2 n} & b\_{2} \\\\\\
|
||
\\ldots & \\ldots & \\ldots & \\ldots & \\ldots \\\\\\
|
||
a\_{m 1} & a\_{m 2} & \\ldots & a\_{m n} & b\_{m}
|
||
\\end{array}\\right\]
|
||
$$
|
||
|
||
这样我们就得到了$A$矩阵的增广矩阵$\\widetilde{A}$ ,可以表示为$(A, B)$,这里的$B$表示的是方程组常数项所构成的列向量,也就是$m×1$的$m$行$1$列矩阵:
|
||
|
||
$$
|
||
B=\\left|\\begin{array}{l}
|
||
b\_{1} \\\\\\
|
||
b\_{2} \\\\\\
|
||
\\cdots \\\\\\
|
||
b\_{m}
|
||
\\end{array}\\right|
|
||
$$
|
||
|
||
如果设$X$为$n×1$的$n$行$1$列矩阵:
|
||
|
||
$$
|
||
X=\\left|\\begin{array}{c}
|
||
x\_{1} \\\\\\
|
||
x\_{2} \\\\\\
|
||
\\cdots \\\\\\
|
||
x\_{n}
|
||
\\end{array}\\right|
|
||
$$
|
||
|
||
那么线性方程组$A$,就可以表示为$AX=B$的矩阵形式。如果我们再换一种表示形式,设:$a\_{1} ,a\_{2},\\ldots, a\_{n},\\beta$表示增广矩阵$\\widetilde{A}$ 的列向量,则线性方程组$A$又可表示为$a\_{1} x\_{1}+a\_{2} x\_{2}+\\cdots+a\_{n} x\_{n}=β$。
|
||
|
||
线性方程组的矩阵和向量形式都是线性方程组的其他表达形式。在工作中,你可以用它们来简化求解,甚至可以提升计算效率,就如之前提到的神经网络的隐藏层的输出计算、图形图像的三维空间变换。在数学中也是同样的,你可以经常运用它们来简化求解。具体线性方程组求解的内容比较多,我们下一节课再来详细讲解求解过程。
|
||
|
||
通过前面的讲解,我相信你对矩阵有了一定的了解,现在我们再回头来看看矩阵的定义吧。
|
||
|
||
矩阵的定义是:一个$(m, n)$矩阵$A$,是由$m×n$个元素组成,$m$和$n$是实数,其中元素$a\_{i j}, \\mathrm{i}=1, \\ldots, \\mathrm{m}, \\mathrm{j}=1, \\ldots, \\mathrm{n}$按$m$行$n$列的矩形排布方式后可以形成矩阵$A$:
|
||
|
||
$$
|
||
A=\\left\[\\begin{array}{cccc}
|
||
a\_{11} & a\_{12} & \\ldots & a\_{1 n} \\\\\\
|
||
a\_{21} & a\_{22} & \\ldots & a\_{2 n} \\\\\\
|
||
\\ldots & \\ldots & \\ldots & \\ldots \\\\\\
|
||
a\_{m 1} & a\_{m 2} & \\ldots & a\_{m n}
|
||
\\end{array}\\right\]
|
||
$$
|
||
|
||
其中$a\_{i j}$属于实数或复数,在我们的场景中是实数$R$,按通常的惯例,$(1, n)$矩阵叫做行,$(m, 1)$矩阵叫做列,这些特殊的矩阵叫做行或列向量。
|
||
|
||
定义完矩阵后,我接着讲一个比较有趣的概念,矩阵转换(Matrix transformation)。矩阵转换经常被用在计算机图形图像的转换中,比如,一张彩色图片从RGB角度来说是三维的,如果要转换成灰度图片,也就是一维图片,那就要做矩阵转换。
|
||
|
||
我们来看一下矩阵转换的过程。设$\\mathrm{R}^{m \\times n}$是实数矩阵$(m, n)$的集合,$A \\in \\mathrm{R}^{m \\times n}$可以表示成另一种形式 $a \\in \\mathrm{R}^{mn}$ 。我们把矩阵的$n$列堆叠成一个长向量后完成转换。这个转换也叫做reshape,其实就是重新调整原矩阵的行数、列数和维数,但是元素个数不变。
|
||
|
||
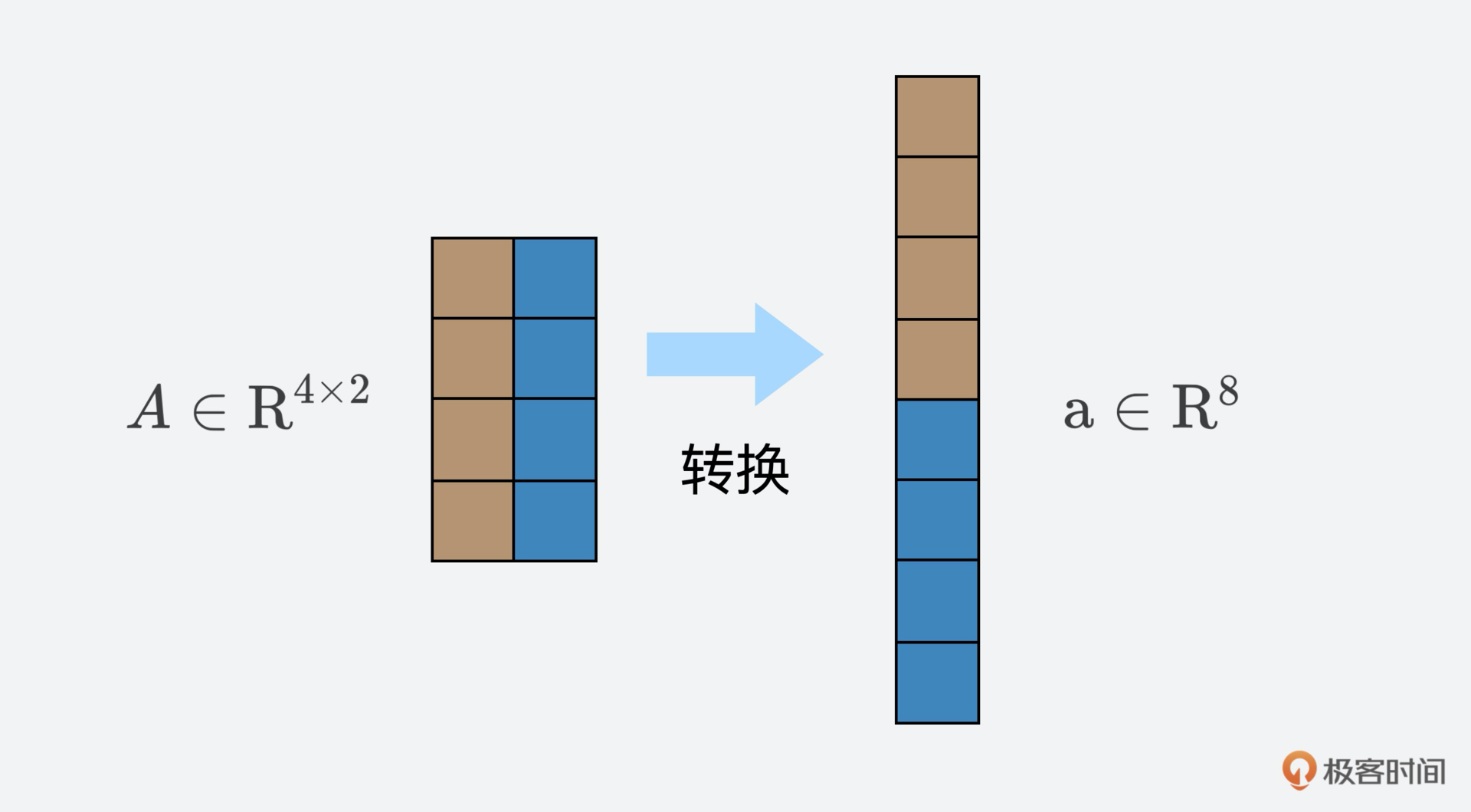
|
||
|
||
## 矩阵的运算
|
||
|
||
了解了矩阵的基本定义后,我们才能进入矩阵的运算环节,就是矩阵的加和乘。
|
||
|
||
加运算很简单,两个矩阵$A \\in \\mathrm{R}^{m \\times n}$,$B \\in \\mathrm{R}^{m \\times n}$的加运算其实就是矩阵各自元素的加。
|
||
|
||
$$
|
||
A+B=\\left\[\\begin{array}{ccc}
|
||
a\_{11}+b\_{11} & \\ldots & a\_{1 n}+b\_{1 n} \\\\\\
|
||
\\cdot & & \\cdot \\\\\\
|
||
\\cdot & & \\cdot \\\\\\
|
||
\\cdot & & \\cdot \\\\\\
|
||
a\_{m 1}+b\_{m 1} & \\ldots & a\_{m n}+b\_{m n}
|
||
\\end{array}\\right\] \\in R^{m \\times n}
|
||
$$
|
||
|
||
我推荐你使用NumPy的einsum来高效地做这类运算,因为它在速度和内存效率方面通常可以超越我们常见的array函数。
|
||
|
||
```
|
||
C= np.einsum('il, lj', A, B)
|
||
|
||
```
|
||
|
||
接下来,我们一起来看看矩阵的乘。这里你需要注意,矩阵的乘和通常意义上“数之间的乘”不同,矩阵的乘有多种类型,这里我讲三种最普遍,也是在各领域里用得最多的矩阵乘。
|
||
|
||
### 1.普通矩阵乘
|
||
|
||
普通矩阵乘是应用最广泛的矩阵乘,两个矩阵$A \\in \\mathrm{R}^{m \\times n}$,$B \\in \\mathrm{R}^{n \\times k}$,普通矩阵则乘可以表示为$C=A B \\in R^{m \\times k}$,$C$中元素的计算规则是矩阵$A$、$B$对应两两元素乘积之和。
|
||
|
||
$$
|
||
c\_{i j}=\\sum\_{k=1}^{n} a\_{i k} b\_{k j}, i=1, \\ldots, m, j=1, \\ldots, l
|
||
$$
|
||
|
||
我们举例来说明。$C$的第一个元素$c\_{11}=a\_{11} \\times b\_{11}+a\_{12} \\times b\_{21}+a\_{13} \\times b\_{31}=1 \\times 1+2 \\times 2+3 \\times 3$。
|
||
|
||
$$
|
||
C=A B=\\left\[\\begin{array}{lll}
|
||
1 & 2 & 3 \\\\\\
|
||
4 & 5 & 6
|
||
\\end{array}\\right\]\\left\[\\begin{array}{ll}
|
||
1 & 4 \\\\\\
|
||
2 & 5 \\\\\\
|
||
3 & 6
|
||
\\end{array}\\right\]=\\left\[\\begin{array}{lll}
|
||
1 \\times 1+2 \\times 2+3 \\times 3 & 1 \\times 4+2 \\times 5+3 \\times 6 \\\\\\
|
||
4 \\times 1+5 \\times 2+6 \\times 3 & 4 \\times 4+5 \\times 5+6 \\times 6
|
||
\\end{array}\\right\]=\\left\[\\begin{array}{cc}
|
||
14 & 32 \\\\\\
|
||
32 & 77
|
||
\\end{array}\\right\]
|
||
$$
|
||
|
||
这里需要特别注意的是,只有相邻阶数匹配的矩阵才能相乘,例如,一个$n×k$矩阵$A$和一个$k×m$矩阵$B$相乘,最后得出$n×m$矩阵$C$,而这里的$k$就是相邻阶数。
|
||
|
||
$$AB=C$$
|
||
|
||
但反过来B和A相乘就不行了,因为相邻阶数$m$不等于$n$。
|
||
|
||
### 2.哈达玛积
|
||
|
||
哈达玛积理解起来就很简单了,就是矩阵各对应元素的乘积,$c\_{i j}=a\_{i j} × b\_{i j}$ 。举个例子:
|
||
|
||
$$
|
||
C=A^{\*} B=\\left\[\\begin{array}{ll}
|
||
1 & 2 \\\\\\
|
||
4 & 5
|
||
\\end{array}\\right\]\\left\[\\begin{array}{ll}
|
||
1 & 4 \\\\\\
|
||
2 & 5
|
||
\\end{array}\\right\]=\\left\[\\begin{array}{cc}
|
||
1 \* 1 & 2 \* 4 \\\\\\
|
||
4 \* 2 & 5 \* 5
|
||
\\end{array}\\right\]=\\left\[\\begin{array}{cc}
|
||
1 & 8 \\\\\\
|
||
8 & 25
|
||
\\end{array}\\right\]
|
||
$$
|
||
|
||
哈达玛积其实在数学中不常看到,不过,在编程中哈达玛积非常有用,因为它可以用来同时计算多组数据的乘积,计算效率很高。
|
||
|
||
### 3.克罗内克积
|
||
|
||
克罗内克积是以德国数学家利奥波德·克罗内克(Leopold Kronecker)的名字命名的。它可以应用在解线性矩阵方程和图像处理方面,当然从更时髦的角度说,它还能用在量子信息领域,我们也称之为直积或张量积。
|
||
|
||
和普通矩阵乘和哈达玛积不同的是,克罗内克积是两个任意大小矩阵间的运算,表示为$A×B$,如果$A$是一个$m × n$的矩阵,而$B$是一个$p×q$的矩阵,克罗内克积则是一个$mp×nq$的矩阵。
|
||
|
||
接下来我们需要定义一个**在矩阵的乘法中起着特殊作用**的矩阵,它就是**单位矩阵**。高等代数中,在求解相应的矩阵时,若添加单位矩阵,通过初等变换进行求解,往往可以使问题变得简单。按照百度百科的解释,单位矩阵如同数的乘法中的$1$,这种矩阵就被称为单位矩阵。它是个方阵,从左上角到右下角的对角线,也就是主对角线上的元素均为$1$,除此以外全都为$0$。
|
||
|
||
在线性代数中,大小为$n$的单位矩阵就是在主对角线上均为1,而其他地方都是$0$的$n×n$的方阵,它用$\\mathrm{I}\_{n}$表示,表达时为了方便可以忽略阶数,直接用$\\mathrm{I}$来表示:
|
||
|
||
$$
|
||
I\_{1}=\[1\], I\_{2}=\\left\[\\begin{array}{ll}
|
||
1 & 0 \\\\\\
|
||
0 & 1
|
||
\\end{array}\\right\], I\_{3}=\\left\[\\begin{array}{lll}
|
||
1 & 0 & 0 \\\\\\
|
||
0 & 1 & 0 \\\\\\
|
||
0 & 0 & 1
|
||
\\end{array}\\right\], …, I\_{n}=\\left\[\\begin{array}{cccc}
|
||
1 & 0 & … & 0 \\\\\\
|
||
0 & 1 & … & 0 \\\\\\
|
||
. & . & … & . \\\\\\
|
||
. & . & . & . \\\\\\
|
||
0 & 0 & … & 1
|
||
\\end{array}\\right\]
|
||
$$
|
||
|
||
## 矩阵的性质
|
||
|
||
在了解了矩阵加和乘,以及单位矩阵后,我们是时候来看一看矩阵的性质了。了解矩阵的性质是进行矩阵计算的前提,就像我们小时候学加减乘除四则运算法则时那样。所以,这块内容对你来说应该不难,你作为了解就好,重点是之后的运算。
|
||
|
||
### 1.结合律
|
||
|
||
任意实数$m×n$矩阵$A$,$n×p$矩阵$B$,$p×q$矩阵$C$之间相乘,满足结合律$(AB)C=A(BC)$。这个很好理解,我就不多说了。
|
||
|
||
$$\\forall A \\in R^{m \\times n}, B \\in R^{n \\times p}, C \\in R^{p \\times q}:(A B) C=A(B C)$$
|
||
|
||
### 2.分配律
|
||
|
||
任意实数$m×n$矩阵$A$和$B$,$n×p$矩阵$C$和$D$之间相乘满足分配律$(A+B)C=AC+BC$,$A(C+D)=AC+AD$。
|
||
|
||
$$
|
||
\\forall \\mathrm{A}, B \\in \\mathrm{R}^{m \\times n}, C, D \\in \\mathrm{R}^{n \\times p}:(A+B) C=A C+B C, A(C+D)=A C+A D
|
||
$$
|
||
|
||
### 3.单位矩阵乘
|
||
|
||
任意实数$m×n$矩阵A和单位矩阵之间的乘,等于它本身$A$。
|
||
|
||
$$
|
||
\\forall A \\in R^{m \\times n}: I\_{m} A=A I\_{n}=A
|
||
$$
|
||
|
||
注意,这里的行和列不同,$m \\neq n$意味着,根据矩阵乘,左乘和右乘单位矩阵也不同,也就是$I\_{m} \\neq I\_{n}$。
|
||
|
||
## 逆矩阵与转置矩阵
|
||
|
||
了解矩阵基本概念、运算,以及性质后,我来讲一讲矩阵应用中的两个核心内容——逆矩阵和转置矩阵。逆矩阵和转置矩阵在实际应用中大有用处,比如:坐标系中的图形变换运算。我们先来看下什么是逆矩阵。
|
||
|
||
### 逆矩阵
|
||
|
||
下面这个图你应该非常熟悉了,图中表现的是数字的倒数,$2$的倒数是$\\frac{1}{2}$,$\\frac{1}{2}$的倒数是$2$。
|
||
|
||
|
||
|
||
其实逆矩阵也有着类似的概念,只不过是写法不一样,我们会把逆矩阵写成$A^{-1}$。那为什么不是$\\frac{1}{A}$呢?那是因为数字1无法被矩阵除。
|
||
|
||
|
||
|
||
我们知道,$2$乘以它的倒数$\\frac{1}{2}$等于$1$。同样的道理,$A$乘以它的逆矩阵$A^{-1}$就等于单位矩阵,即$\\mathrm{A} \\times A^{-1}=\\mathrm{I}$($I$即单位矩阵),反过来也一样,$\\mathrm{A}^{-1} \\times A=\\mathrm{I}$。
|
||
|
||
为方便你理解,我用一个$2 \\times 2$矩阵$A$来解释一下逆矩阵的算法。首先,我们交换$a\_{11}$和$a\_{22}$的位置,然后在$a\_{12}$和$a\_{21}$前加上负号,最后除以行列式$a\_{11} a\_{22}-a\_{12} a\_{21}$。
|
||
|
||
$$
|
||
A^{-1}=\\left\[\\begin{array}{ll}
|
||
a\_{11} & a\_{12} \\\\\\
|
||
a\_{21} & a\_{22}
|
||
\\end{array}\\right\]^{-1}=\\frac{1}{a\_{11} a\_{22}-a\_{12} a\_{21}}\\left\[\\begin{array}{cc}
|
||
a\_{22} & -a\_{12} \\\\\\
|
||
\-a\_{21} & a\_{11}
|
||
\\end{array}\\right\]
|
||
$$
|
||
|
||
那我们该如何验证这是不是正解呢?
|
||
|
||
方法其实很简单,记得刚才的公式就行,$\\mathrm{A} \\times A^{-1}=\\mathrm{I}$。现在我们就代入公式来验证一下,$A$和它的逆矩阵相乘,通过刚才的算法最终得出的结果是单位矩阵。
|
||
|
||
$$
|
||
A \\times A^{-1}=\\left\[\\begin{array}{llll}
|
||
a\_{11} & a\_{12} \\\\\\
|
||
a\_{21} & a\_{22}
|
||
\\end{array}\\right\]\\left\[\\begin{array}{ll}
|
||
a\_{11} & a\_{12} \\\\\\
|
||
a\_{21} & a\_{22}
|
||
\\end{array}\\right\]^{-1}=\\left\[\\begin{array}{ll}
|
||
a\_{11} & a\_{12} \\\\\\
|
||
a\_{21} & a\_{22}
|
||
\\end{array}\\right\]\\left\[\\begin{array}{lll}
|
||
\\frac{a\_{22}}{a\_{11} a\_{22}-a\_{12} a\_{21}} & \\frac{-a\_{12}}{a\_{11} a\_{22}-a\_{12} a\_{21}} \\\\\\
|
||
\\frac{-a\_{21}}{a\_{11} a\_{22}-a\_{12} a\_{21}} & \\frac{a\_{11}}{a\_{11} a\_{22}-a\_{12} a\_{21}}
|
||
\\end{array}\\right\]=\\left\[\\begin{array}{ll}
|
||
\\frac{a\_{11} \\times a\_{22}}{a\_{11} a\_{22}-a\_{12} a\_{21}}+\\frac{a\_{12} ×(-a\_{21})}{a\_{11} a\_{22}-a\_{12} a\_{21}} & \\frac{a\_{11} ×(-a\_{12})}{a\_{11} a\_{22}-a\_{12} a\_{21}}+\\frac{a\_{12} \\times a\_{11}}{a\_{11} a\_{22}-a\_{12} a\_{21}} \\\\\\
|
||
\\frac{a\_{21} \\times a\_{22}}{a\_{11} a\_{22}-a\_{12} a\_{21}}+\\frac{a\_{22} ×(-a\_{21})}{a\_{11} a\_{22}-a\_{12} a\_{21}} & \\frac{a\_{21} ×(-a\_{12})}{a\_{11} a\_{22}-a\_{12} a\_{21}}+\\frac{a\_{22} × a\_{11}}{a\_{11} a\_{22}-a\_{12} a\_{21}}
|
||
\\end{array}\\right\]=\\left\[\\begin{array}{lll}
|
||
1 & 0 \\\\\\
|
||
0 & 1
|
||
\\end{array}\\right\]
|
||
$$
|
||
|
||
这里有一点需要特别说明,不是每一个矩阵都是可逆的。如果一个矩阵是可逆的,那这个矩阵我们叫做**非奇异矩阵**,如果一个矩阵是不可逆的,那这个矩阵我们就叫做**奇异矩阵**,而且如果一个矩阵可逆,那它的逆矩阵必然是唯一的。
|
||
|
||
还记得行列式$a\_{11} a\_{22}-a\_{12} a\_{21}$吗?如果我们要证明矩阵是可逆的,只要证明行列式不等于零就行。更高阶的逆矩阵的算法也是一样的原理。
|
||
|
||
最后,我想通过一个现实生活中的案例来让你更多地了解逆矩阵。
|
||
|
||
一个旅游团由孩子和大人组成,去程他们一起做大巴,每个孩子的票价$3$元,大人票价$3.2$元,总共花费$118.4$元。回程一起做火车,每个孩子的票价$3.5$元,大人票价$3.6$元,总共花费$135.2$元。请问旅游团里有多少小孩和大人?
|
||
|
||
首先,我们设置一些矩阵,组成线性方程$XA=B$。
|
||
|
||

|
||
|
||
要解$X$,我们就要先计算$A$的逆矩阵$A^{-1}$:
|
||
|
||
$$
|
||
A^{-1}=\\left\[\\begin{array}{cc}
|
||
3 & 3.5 \\\\\\
|
||
3.2 & 3.6
|
||
\\end{array}\\right\]^{-1}=\\frac{1}{3 \\times 3.6-3.5 \\times 3.2}\\left\[\\begin{array}{cc}
|
||
3.6 & -3.5 \\\\\\
|
||
\-3.2 & 3
|
||
\\end{array}\\right\]=\\left\[\\begin{array}{cc}
|
||
\-9 & 8.75 \\\\\\
|
||
8 & -7.5
|
||
\\end{array}\\right\]
|
||
$$
|
||
|
||
接下来再计算$X=B A^{-1}$:
|
||
|
||
$$
|
||
\\left\[\\begin{array}{ll}
|
||
x\_{1} & x\_{2}
|
||
\\end{array}\\right\]=\\left\[\\begin{array}{ll}
|
||
118.4 & 135.2
|
||
\\end{array}\\right\]\\left\[\\begin{array}{cc}
|
||
\-9 & 8.75 \\\\\\
|
||
8 & -7.5
|
||
\\end{array}\\right\]=\\left\[\\begin{array}{ll}
|
||
16 & 22
|
||
\\end{array}\\right\]
|
||
$$
|
||
|
||
最终,我们得出这个旅游团有16个小孩和22个大人。
|
||
|
||
这也是解线性方程组的一种方法,类似这样的计算被广泛应用在各领域中,比如建筑工程、游戏和动画的3D效果上。虽然现在有很多程序包封装了这类数学计算的底层实现,但如果你能很好地理解这些概念,就可以为编程或算法调优打下坚实的基础。
|
||
|
||
Last but not least,方程次序很重要,也就是说,$AX=B$和$XA=B$的结果是不同的,这个一定要牢记哦!
|
||
|
||
### 转置矩阵
|
||
|
||
一般伴随逆矩阵之后出现的就是转置矩阵。在计算机图形图像处理中,如果要对一个物体进行旋转、平移、缩放等操作,就要对描述这个物体的所有矩阵进行运算,矩阵转置就是这类运算之一,而矩阵的转置在三维空间中的解释就相当于“得到关于某个点对称的三维立体”。所以,转置矩阵的定义很简单。
|
||
|
||
将矩阵的行列互换,得到的新矩阵就叫做转置矩阵(transpose)。转置矩阵的行列式不变。我们把$m×n$矩阵$A$的行列互换,得到转置矩阵$A^{T}$。
|
||
|
||
$$
|
||
A=\\left\[\\begin{array}{cccc}
|
||
a\_{11} & a\_{12} & \\ldots & a\_{1 n} \\\\\\
|
||
a\_{21} & a\_{22} & \\ldots & a\_{2 n} \\\\\\
|
||
\\ldots & \\ldots & \\ldots & \\ldots \\\\\\
|
||
a\_{m 1} & a\_{m 2} & \\ldots & a\_{m n}
|
||
\\end{array}\\right\]
|
||
$$
|
||
|
||
$$
|
||
A^{T}=\\left\[\\begin{array}{cccc}
|
||
a\_{11} & a\_{21} & \\ldots & a\_{m 1} \\\\\\
|
||
a\_{12} & a\_{22} & \\ldots & a\_{m 2} \\\\\\
|
||
\\ldots & \\ldots & \\ldots & \\ldots \\\\\\
|
||
a\_{1 n} & a\_{2 n} & \\ldots & a\_{m n}
|
||
\\end{array}\\right\]
|
||
$$
|
||
|
||
最后,为了方便你理解,我们再总结一下逆矩阵和转置矩阵的性质。你不用死记硬背,重在理解。
|
||
|
||
1. 矩阵和自身逆矩阵相乘得道单位矩阵,$A A^{-1}=I=A^{-1} A$;
|
||
2. $A$$B$两矩阵相乘的逆,等于逆矩阵$B$和逆矩阵$A$相乘,这里强调一下乘的顺序很重要,$(A B)^{-1}=B^{-1} A^{-1}$;
|
||
3. $AB$两矩阵相加后的逆矩阵,不等于各自逆矩阵的相加, $(A+B)^{-1} \\neq A^{-1}+B^{-1}$;
|
||
4. 矩阵转置的转置还是它本身,$\\left(A^{T}\\right)^{\\mathrm{T}}=A$;
|
||
5. $AB$两矩阵相加后的转置矩阵,等于各自转置矩阵的相加,$(A+B)^{T}=A^{T}+B^{T}$;
|
||
6. $AB$两矩阵相乘后的转置矩阵,等于转置矩阵B和转置矩阵A的相乘,这里再次强调乘的顺序很重要,$(A B)^{T}=B^{T} A^{T}$。
|
||
|
||
## 本节小结
|
||
|
||
好了,到这里矩阵这一讲就结束了,最后我再带你总结一下前面讲解的内容。
|
||
|
||
今天的知识,你只需要知道矩阵是线性方程组的另一种表达,了解和掌握矩阵的定义和性质就足够了。当然,矩阵还有很多内容,但我认为掌握了我讲的这些内容后,就为以后的一些矩阵应用场景打下了坚实的数学基础,也是下一讲的解线性方程组的前置知识。
|
||
|
||
|
||
|
||
## 线性代数练习场
|
||
|
||
对于10维列向量$x=\\left(x\_{1}, \\ldots, x\_{10}\\right)^{T}$, $v=\\left(v\_{1}, \\ldots, v\_{10}\\right)^{T}$,如果要计算$y=x x^{T}\\left(I+v v^{T}\\right) x$,其中$I$是10阶单位矩阵。你会怎么做?
|
||
|
||
友情提醒,这里有多种方式解题。你能不能找到一个最简单的方法来解这道题?虽然结果很重要,但我想说的是过程更重要,而且往往解题过程不同,从计算机角度来说,运算的效率会有极大的不同。
|
||
|
||
欢迎你在留言区晒出你的运算过程和结果。如果有收获,也欢迎你把这篇文章分享给你的朋友。
|
||
|