375 lines
25 KiB
Markdown
375 lines
25 KiB
Markdown
# 17|集成学习:机器学习模型如何“博采众长”?
|
||
|
||
你好,我是黄佳。恭喜你连闯4关,成功来到最后一关“裂变关”。
|
||
|
||
回忆一下这一路的旅程,在获客关中,我们给用户分组画像;在变现关中,我们关注用户的生命周期价值;在激活关中,我们预测了App的激活数字;在留存关中,我们分析了与用户流失相关的因素。
|
||
|
||
|
||
|
||
那么在裂变关中,我们将从数据中寻找蛛丝马迹,发现“易速鲜花”运营中最佳的“裂变方案”。不过,除了介绍运营中的裂变方案外,今天,我们还要好好讲一讲集成学习。
|
||
|
||
为什么要专门拿出一讲来谈集成学习呢?我们在[第9讲](https://time.geekbang.org/column/article/419218)说过,我们用机器学习建模的过程,就是和过拟合现象持续作斗争的过程。而集成学习在机器学习中是很特别的一类方法,能够处理回归和分类问题,而且它对于避免模型中的过拟合问题,具有天然的优势。那么,集成学习的优势是怎么形成的?学习了今天的课程后你就会找到答案。
|
||
|
||
## 定义问题
|
||
|
||
老规矩,我们先来定义今天要解决的问题。
|
||
|
||
说起裂变,你可能并不会感到陌生。裂变是让产品自循环、自传播的重要工具。像邀请新人得红包、分享App领优惠券、友情助力拿赠品、朋友圈打卡退学费等等,都是裂变的玩法。
|
||
|
||
最近,“易速鲜花”运营部门提出了两个裂变思路。方案一是选择一批热销商品,让老用户邀请朋友扫码下载App并成功注册,朋友越多,折扣越大。我们把这个方案命名为“疯狂打折”,它走的是友情牌。方案二是找到一个朋友一起购买,第二件商品就可以免费赠送,这叫“买一送一”。
|
||
|
||
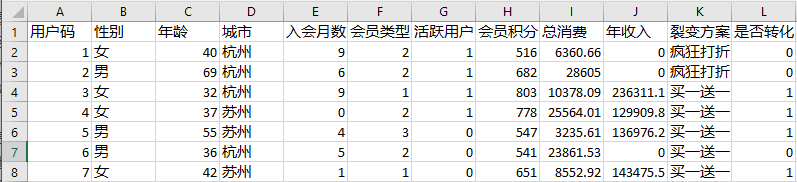
提出两个裂变方案之后,运营部门收集了[转化数据](https://github.com/huangjia2019/geektime/tree/main/%E8%A3%82%E5%8F%98%E5%85%B317)。那么,我们今天的目标就是**根据这个数据集,来判断一个特定用户在特定的裂变促销之下,是否会转化。**
|
||
|
||
|
||
|
||
这个问题和我们之前预测用户是否会流失非常相似,也是一个二元分类问题。
|
||
|
||
下面我们就导入相关的包,并读入数据:
|
||
|
||
```
|
||
import pandas as pd #导入Pandas
|
||
import numpy as np #导入NumPy
|
||
df_fission = pd.read_csv('易速鲜花裂变转化.csv') #载入数据
|
||
df_fission.head() #显示数据
|
||
|
||
```
|
||
|
||
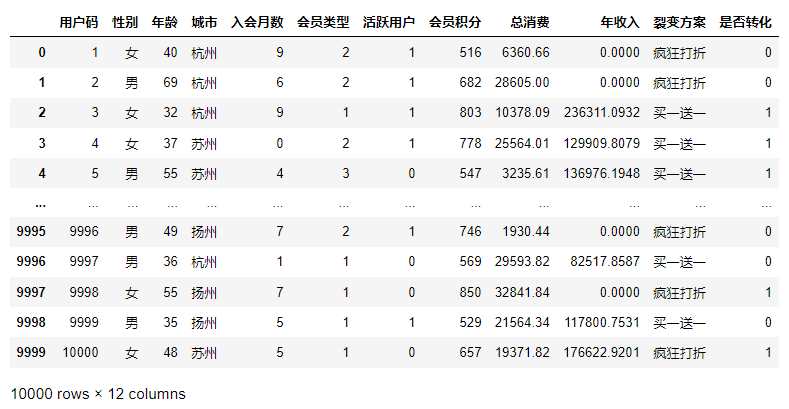
输出如下:
|
||
|
||
|
||
|
||
在这个数据集中,共有10000个数据样本,也就是10000个用户的信息。其他字段都很好理解,我们重点来看看“裂变方案”字段。这个字段表示的是该用户所导流到的裂变类型,一个用户看到的是“疯狂打折”优惠页,还是“买一送一”优惠页,是随机分配的结果。对于一个用户,二者只能属于其一。而与之对应的“是否转化”字段就**是我们用来预测转化率的标签****了****。**
|
||
|
||
下面我们进入数据可视化和预处理的环节。
|
||
|
||
## 数据可视化和预处理
|
||
|
||
在数据可视化部分,我只想看一看转化和未转化的比例,也就是购买产品和未购买产品的比例。看这个比例是为了看这个数据集中的各类别样本数是否平衡。
|
||
|
||
```
|
||
import matplotlib.pyplot as plt #导入pyplot模块
|
||
import seaborn as sns #导入Seaborn
|
||
fig = sns.countplot('是否转化', data=df_fission) #创建柱状计数图
|
||
fig.set_ylabel("数目") #Y轴标题
|
||
plt.show() #显示图像
|
||
|
||
```
|
||
|
||
输入如下:
|
||
|
||
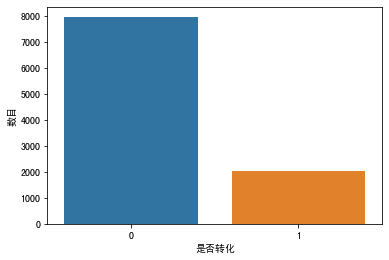
|
||
|
||
结果显示,在10000个用户中,大概有2000个用户购买了产品,转化率大概在20%。说明运营人员给我们的是一个并不平衡的分类数据集。这个结论将为我们后续的算法选择做出指导。
|
||
|
||
下面,我们把数据集中的类别变量,转变为机器学习模型能够读取的虚拟变量(也叫哑编码或哑变量):
|
||
|
||
```
|
||
# 把二元类别文本数字化
|
||
df_fission['性别'].replace("女",0,inplace = True)
|
||
df_fission['性别'].replace("男",1,inplace=True)
|
||
# 显示数字类别
|
||
print("Gender unique values",df_fission['性别'].unique())
|
||
# 把多元类别转换成多个二元哑变量,然后贴回原始数据集
|
||
df_fission = pd.get_dummies(df_fission, drop_first = True)
|
||
df_fission # 显示数据集
|
||
|
||
```
|
||
|
||
输出如下:
|
||
|
||

|
||
|
||
然后,我们再来构建标签和特征数据集,并拆分出训练集和测试集,最后对特征进行归一化缩放。我们对这些步骤已经非常熟悉了,我就不需再过多解释了:
|
||
|
||
```
|
||
X = df_fission.drop(['用户码','是否转化'], axis = 1) # 构建特征集
|
||
y = df_fission.是否转化.values # 构建标签集
|
||
from sklearn.model_selection import train_test_split
|
||
X_train, X_test, y_train, y_test = train_test_split(X,y,test_size = 0.2)
|
||
from sklearn.preprocessing import MinMaxScaler #导入归一化缩放器
|
||
scaler = MinMaxScaler() #创建归一化缩放器
|
||
X_train = scaler.fit_transform(X_train) #拟合并转换训练集数据
|
||
X_test = scaler.transform(X_test) #转换测试集数据
|
||
|
||
```
|
||
|
||
这样,数据集就准备好啦,现在,我们进入算法选择环节。
|
||
|
||
## 算法选择:集成学习
|
||
|
||
我们前面说,判断一个特定用户在特定的裂变促销之下是否会转化,属于二元分类问题。对于二分类问题,我们在[第15讲](https://time.geekbang.org/column/article/423893)中也提到过,它不仅可以用逻辑回归解决,还可以通过SVM、集成学习、神经网络等多种模型完成。现在,我们就借助这一讲的项目,着重来了解一下集成学习方法的原理和应用。
|
||
|
||
**集成学习(ensemble learning),是通过构建出多个模型(这些模型可以是比较弱的模型),然后将它们组合起来完成任务的机器学习算法**。所以,它实际上并不是一种机器学习算法,而是一个机器学习算法的家族。通常情况下,集成学习将几个表现一般的模型集成在一起,就能大幅提升模型的性能,这就是集成学习的天然优势。
|
||
|
||
在这个算法家族中,很多算法都是“网红”算法,比如随机森林、梯度提升机(英文叫GB或GBDT)和极限梯度提升(eXtreme Gradient Boosting,即XGBoost,有时候简称XGB)等,这些都是非常流行的机器学习算法,在很多许多领域都取得了成功,并且还是很多人赢得各种机器学习竞赛的主要方法。
|
||
|
||
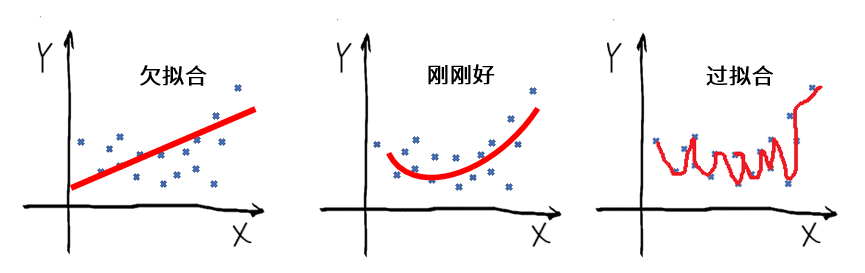
那么,为什么几个表现一般的模型集成在一起,性能会大幅提升?下面,我们来探究一下。首先,请你回忆一下,我们在[第9讲](https://time.geekbang.org/column/article/419218)中讲过,机器学习在训练时有一个从欠拟合到过拟合的过程:
|
||
|
||
|
||
|
||
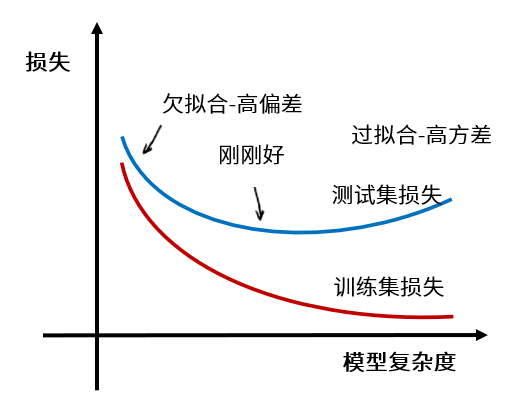
如果结合我们已经比较熟悉的损失曲线,就可以用下面这张图来描述这一过程:
|
||
|
||
|
||
|
||
我们说,当给定一个学习任务,在训练初期,模型对训练集的拟合还未完善,训练集和测试集上面的损失也都比较大,这时候的模型处于欠拟合状态。由于模型的拟合能力还不强,数据集的改变是无法使模型的效率产生显著变化的,所以,如果我们把此时的模型应用于训练集和测试集的数据,都会出现“**高偏差**”。
|
||
|
||
随着训练次数增多,模型的拟合能力在调整优化的过程中会变得越来越强,训练集上和测试集上的损失也都会不断下降。
|
||
|
||
当充分训练之后,模型已经完全拟合了训练集数据,训练集上的损失也变得非常小。但是,这时候的模型很容易受数据的影响,数据的轻微扰动都会导致模型发生显著变化。这时候,如果我们把模型应用于不同的数据集(包括测试集),会出现**很高的方差**,也就是过拟合的状态。
|
||
|
||
总的来说就是,模型在欠拟合状态会出现“高偏差”,在过拟合状态会出现“高方差”,这都不符合我们的预期。只有在拟合刚刚好的时候,模型才是相对成功的。这时候,模型的偏差和方差处于平衡态,均不会太高。
|
||
|
||
你可能注意到,在上面的讲述中,我引入了“方差”和“偏差”这两个新概念。方差,是从统计学中引用过来的概念,它表示的是一组数据距离其均值的离散程度。而“偏差”是机器学习里概念,用来衡量模型的准确程度。
|
||
|
||
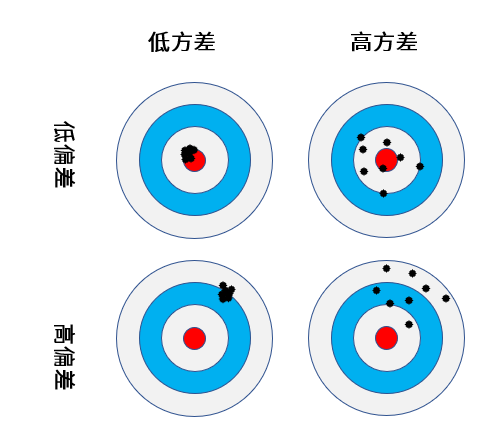
在机器学习中,“低偏差”和“低方差”是我们希望达到的效果。可是,一般来说, 低偏差与低方差是鱼与熊掌不可兼得的,这被称作偏差-方差窘境 (bias-variance dilemma)。下面这张打靶图,就形象地说明了这一点:
|
||
|
||
|
||
其实,机器学习性能优化领域的最核心问题,就是不断地在“欠拟合-过拟合”之间,也就是“偏差-方差”之间,探求最佳平衡点,换句话说,就是训练集优化和测试集泛化的平衡点。而机器学习的性能优化是有顺序的,我们一般是先减小偏差,再聚焦于降低方差。
|
||
|
||
那说了这么多,你也许有点不耐烦了:这些内容和集成学习到底有什么关系呢?
|
||
|
||
其实啊,集成学习的优点就在于,它可以通过组合一些比较简单的算法,来保留这些算法训练出的模型“方差低”的优势;在此基础之上,集成学习又能引入复杂的模型,来扩展简单算法的预测空间。所以,集成学习是同时减小方差和偏差的大招。
|
||
|
||
集成学习的核心思想是训练出多个模型并将这些模型进行组合。根据分类器的训练方式和组合预测的方法,集成学习中两种最重要的方法就是:降低偏差的Boosting和降低方差的Bagging。
|
||
|
||
下面,我们就一边讲解这两种方法,一边用它们来解决“特定用户在特定的裂变促销之下是否会转化成功”的预测问题。
|
||
|
||
我们先来看Boosting。
|
||
|
||
## 降低偏差:Boosting方法
|
||
|
||
Boosting方法是把梯度下降的思想应用在了机器学习算法的优化上,让弱模型对数据的拟合逐渐增强。它的基本思路就是:持续地通过新模型来优化同一个基模型(基模型,也就是Boosting开始时的初始模型),当一个新的弱模型加入进来的时候,Boosting就在原有模型的基础上整合这个新模型,然后形成新的基模型。而对这个新的基模型的训练,则会一直聚集于之前模型的误差点(也就是原模型预测出错的样本)上,这样做的目标是不断减小模型的预测误差。
|
||
|
||
在Boosting方法中,有三种很受欢迎的算法,分别是AdaBoost、GBDT 和XGBoost。其中,AdaBoost会对样本进行加权;GBDT在AdaBoost的基础上,还会定义一个损失函数,通过梯度下降来优化模型;而XGBoost则在GBDT的基础上,进一步优化了梯度下降的方式。
|
||
|
||
这三种算法都可以用来解决我们这一讲的分类问题(其实也可以用于回归问题)。下面,我们来逐一做个讲解。
|
||
|
||
### 1\. AdaBoost算法
|
||
|
||
我们先来使用AdaBoost算法。在处理分类问题时,AdaBoost 会先给不同的样本分配不同的权重,被分错的样本的权重在Boosting 过程中会增大,新模型会因此更加关注这些被分错的样本;反之,被分正确的样本的权重会减小。接着,AdaBoost会将修改过权重的新数据集输入到新模型进行训练,产生新的基模型。最后,AdaBoost会把每次得到的基模型组合起来,并根据其分类错误率对模型赋予权重,集成为最终的模型。
|
||
|
||
下面,我们用AdaBoost算法来预测一下用户在特定的裂变促销之下是否会转化,并给出评估分数:
|
||
|
||
```
|
||
from sklearn.ensemble import AdaBoostClassifier # 导入AdaBoost 模型
|
||
dt = DecisionTreeClassifier() # 选择决策树分类器作为AdaBoost 的基准算法
|
||
ada = AdaBoostClassifier(dt) # AdaBoost 模型
|
||
ada.fit(X_train, y_train) # 拟合模型
|
||
y_pred = ada.predict(X_test) # 进行预测
|
||
print("AdaBoost 测试准确率: {:.2f}%".format(ada.score(X_test, y_test)*100))
|
||
print("AdaBoost 测试F1分数: {:.2f}%".format(f1_score(y_test, y_pred)*100))
|
||
|
||
```
|
||
|
||
输出如下:
|
||
|
||
```
|
||
AdaBoost 测试准确率: 78.75%
|
||
AdaBoost 测试F1分数: 50.18%
|
||
|
||
```
|
||
|
||
结果显示,AdaBoost算法测试准确率是78.75%,F1分数为50.18%。这个F1分数并不是很理想,我们需要考虑一下有没有更优的算法。而下面要介绍的GBDT算法就对AdaBoost算法做出了进一步的改进。
|
||
|
||
### 2\. GBDT算法
|
||
|
||
GBDT算法也叫梯度提升(Granding Boosting)算法,它是梯度下降和Boosting方法结合的产物。因为常见的梯度提升都是基于决策树模型(机器学习中就把决策树模型简称为树)的,所以我们这里会把它称作是GBDT,即梯度提升决策树(Granding Boosting Decision Tree)。
|
||
|
||
我们知道,前面的AdaBoost算法只是对样本进行加权,但GBDT 算法与之不同,它还会定义一个损失函数,并对损失和机器学习模型所形成的函数进行求导,每次生成的模型都是沿着前面模型的负梯度方向(一阶导数)进行优化,直到发现全局最优解。也就是说,在GBDT的每一次迭代中,当前的树所学习的内容是之前所有树的结论和损失,在学习中,GBDT会拟合得到一棵新的树,而这棵新的树就相当于是之前每一棵树的效果累加。
|
||
|
||
下面,我们用GBDT算法来预测用户是否转化,并给出评估分数:
|
||
|
||
```
|
||
from sklearn.ensemble import GradientBoostingClassifier # 导入梯度提升模型
|
||
gb = GradientBoostingClassifier() # 梯度提升模型
|
||
gb.fit(X_train, y_train) # 拟合模型
|
||
y_pred = gb.predict(X_test) # 进行预测
|
||
print(" 梯度提升测试准确率: {:.2f}%".format(gb.score(X_test, y_test)*100))
|
||
print(" 梯度提升测试F1分数: {:.2f}%".format(f1_score(y_test, y_pred)*100))
|
||
|
||
```
|
||
|
||
输出如下:
|
||
|
||
```
|
||
梯度提升测试准确率: 87.00%
|
||
梯度提升测试F1 分数: 61.19%
|
||
|
||
```
|
||
|
||
结果显示,GBDT算法的测试准确率是87.00%,F1分数为61.19%。F1分数果然大幅提升,看来GBDT算法还不错。其实,还有比GBDT更厉害的集成学习算法,它就是算法XGBoost算法。
|
||
|
||
### 3\. XGBoost算法
|
||
|
||
XGBoost算法也叫极端梯度提升(eXtreme Gradient Boosting),有时候也直接叫作XGB。它和GBDT 类似,也会定义一个损失函数。不过,不同的是,GBDT 只用到一阶导数信息,而XGBoost会利用泰勒展开式把损失函数展开到二阶后求导。由于利用了二阶导数信息,XGBoost在训练集上的收敛会更快。
|
||
|
||
在使用XGBoost之前,我们需要通过pip语句安装XGBoost包,当然,你也可以在Anaconda的Environments(环境)界面中,直接搜索并安装XGBoost包:
|
||
|
||
```
|
||
pip install xgboost
|
||
|
||
```
|
||
|
||
下面,我们用XGBoost算法来预测用户是否转化,并给出评估分数:
|
||
|
||
```
|
||
from xgboost import XGBClassifier # 导入XGB 模型
|
||
xgb = XGBClassifier() # XGB 模型
|
||
xgb.fit(X_train, y_train) # 拟合模型
|
||
y_pred = xgb.predict(X_test) # 进行预测
|
||
print("XGB 测试准确率: {:.2f}%".format(xgb.score(X_test, y_test)*100))
|
||
print("XGB 测试F1分数: {:.2f}%".format(f1_score(y_test, y_pred)*100))
|
||
|
||
```
|
||
|
||
输出如下:
|
||
|
||
```
|
||
XGB 测试准确率: 87.00%
|
||
XGB 测试F1分数: 63.17%
|
||
|
||
```
|
||
|
||
结果显示,XGBoost算法的测试准确率是87.00%,F1分数为63.17%。
|
||
|
||
可以看出,在上述三种算法中,XGBoost算法的性能是最佳的。虽然它的预测准确率和GBDT相同,但是它的F1分数高,而F1分数是我们更重视的指标。
|
||
|
||
下面,我们再来介绍并使用能降低方差的Bagging方法。
|
||
|
||
## 降低方差:Bagging方法
|
||
|
||
Bagging 是Bootstrap Aggregating 的缩写,有人把它翻译为套袋法、装袋法,或者自助聚合,到现在,还没有一个统一的叫法。所以,我们就直接用它的英文名称Bagging。
|
||
|
||
Bagging算法的基本思想是从原始的数据集中抽取数据,形成K个随机的新训练集,然后训练出K个不同的模型。
|
||
|
||
具体来讲,Bagging算法首先会在原始样本集中随机抽取K轮,每轮抽取n个训练样本作为一个训练集。这时候,有些样本可能被多次抽取,而有些样本可能一次都没有被抽取,这叫做有放回的抽取)。在抽取K轮之后,就会形成K个训练集,注意,这K个训练集是彼此独立的。这个过程也叫作bootstrap(可译为“自举”或“自助采样”)。
|
||
|
||
接着,Bagging算法会每次使用一个训练集,并通过相同的机器学习算法(如决策树、神经网络等)得到一个模型。因为有K个训练集,所以一共可以得到K个模型。我们把这些模型称为“基模型”(base estimator)或者“基学习器”。
|
||
|
||
最后,对于这K个模型,Bagging算法会用不同的方式得到基模型的集成结果:如果是分类问题,Bagging算法会对K个模型投票,进而得到分类结果;如果是回归问题,Bagging算法会计算K个模型的均值,将其作为最后的结果。
|
||
|
||
因为随机抽取数据的方法能减少可能的数据干扰,所以经过Bagging 的模型将会具有“低方差””。一般来说,Bagging有三种常见的算法:决策树的Bagging、随机森林算法和极端随机森林。
|
||
|
||
### 1\. 决策树的Bagging
|
||
|
||
多数情况下的Bagging,都是基于决策树的。构造随机森林的第一步,其实就是对多棵决策树进行Bagging,我们把它称为树的聚合(Bagging of Tree)。
|
||
|
||
决策树这种模型,具有显著的低偏差、高方差的特点。也就是说,决策树模型受数据的影响特别大,一不小心,训练集准确率就接近100% 了,而这种效果又不能移植到其他的数据集上,所以,这是很明显的过拟合现象。集成学习的Bagging算法就是从决策树模型开始,着手解决它太过于精准,又不易泛化的问题。当然,Bagging的原理并不仅限于决策树,它还可以扩展到其他机器学习算法。
|
||
|
||
下面,我们用决策树的Bagging算法来预测用户是否转化,并给出评估分数:
|
||
|
||
```
|
||
from sklearn.ensemble import BaggingClassifier # 导入Bagging 分类器
|
||
from sklearn.tree import DecisionTreeClassifier # 导入决策树分类器
|
||
from sklearn.metrics import (f1_score, confusion_matrix) # 导入评估指标
|
||
dt = BaggingClassifier(DecisionTreeClassifier()) # 只使用一棵决策树
|
||
dt.fit(X_train, y_train) # 拟合模型
|
||
y_pred = dt.predict(X_test) # 进行预测
|
||
print(" 决策树测试准确率: {:.2f}%".format(dt.score(X_test, y_test)*100))
|
||
print(" 决策树测试F1 分数: {:.2f}%".format(f1_score(y_test, y_pred)*100))
|
||
bdt = BaggingClassifier(DecisionTreeClassifier()) # 树的Bagging
|
||
bdt.fit(X_train, y_train) # 拟合模型
|
||
y_pred = bdt.predict(X_test) # 进行预测
|
||
print(" 决策树Bagging 测试准确率: {:.2f}%".format(bdt.score(X_test, y_test)*100))
|
||
print(" 决策树Bagging 测试F1分数: {:.2f}%".format(f1_score(y_test, y_pred)*100))
|
||
|
||
```
|
||
|
||
输出如下:
|
||
|
||
```
|
||
决策树测试准确率: 85.10%
|
||
决策树测试F1分数: 58.17%
|
||
决策树Bagging 测试准确率: 85.55%
|
||
决策树Bagging 测试F1 分数: 58.66%
|
||
|
||
```
|
||
|
||
结果显示,对于这个数据集来说,决策树Bagging的测试集F1分数有提升,但是优势不明显。不过没关系,我们可以试一下更常见的随机森林算法,它其实是经过改进的“决策树Bagging算法”。
|
||
|
||
### 2\. 随机森林算法
|
||
|
||
当我们说到集成学习,最关键的一点是:各个基模型的相关度要小,差异性要大。模型间差异越大(也就是异质性越强),集成的效果越好。两个准确率为99% 的模型,如果其预测结果都一致,也就没有提高的余地了。因此,对决策树做集成,关键就在于各棵树的差异性是否够大。
|
||
|
||
为了实现基模型差异化的目标,随机森林在树分叉时,增加了对特征选择的随机性,而并不总是考量全部的特征。这个小小的改进,就进一步提高了各棵树的差异。
|
||
|
||
下面,我们用随机森林算法来预测用户是否转化,并给出评估分数:
|
||
|
||
```
|
||
from sklearn.model_selectifrom sklearn.ensemble import RandomForestClassifier # 导入随机森林模型
|
||
rf = RandomForestClassifier() # 随机森林模型
|
||
rf.fit(X_train, y_train) # 拟合模型
|
||
y_pred = rf.predict(X_test) # 进行预测
|
||
print(" 随机森林测试准确率: {:.2f}%".format(rf.score(X_test, y_test)*100))
|
||
print(" 随机森林测试F1分数: {:.2f}%".format(f1_score(y_test, y_pred)*100))
|
||
|
||
```
|
||
|
||
输出如下:
|
||
|
||
```
|
||
随机森林测试准确率: 87.20%
|
||
随机森林测试F1分数: 61.79%
|
||
|
||
```
|
||
|
||
可以看到,随机森林测试F1分数很明显地高于决策树模型和决策树的Bagging。
|
||
|
||
### 3\. 极端随机森林算法
|
||
|
||
最后,我们再来看极端随机森林算法。极端森林算法在随机森林的基础上,又增加了进一步的随机性。
|
||
|
||
随机森林算法在树分叉时会随机选取m个特征作为考量,对于每一次分叉,它还会遍历所有的分支,然后选择基于这些特征的最优分支。这在本质上仍属于贪心算法(greedy algorithm),即在每一步选择中都采取在当前状态下最优的选择。而极端随机森林算法则不同,它一点也不“贪心”,它甚至不回去考量所有的分支,而是随机选择一些分支,从中拿到一个最优解。
|
||
|
||
下面,我们用极端随机森林算法来预测用户是否转化,并给出评估分数:
|
||
|
||
```
|
||
from sklearn.ensemble import ExtraTreesClassifier # 导入极端随机森林模型
|
||
ext = ExtraTreesClassifier() # 极端随机森林模型
|
||
ext.fit(X_train, y_train) # 拟合模型
|
||
y_pred = ext.predict(X_test) # 进行预测
|
||
print(" 极端随机森林测试准确率: {:.2f}%".format(ext.score(X_test, y_test)*100))
|
||
print(" 极端随机森林测试F1分数: {:.2f}%".format(f1_score(y_test, y_pred)*100))
|
||
|
||
```
|
||
|
||
输出如下:
|
||
|
||
```
|
||
极端随机森林测试准确率: 87.05%
|
||
极端随机森林测试F1分数: 60.58%
|
||
|
||
```
|
||
|
||
结果显示,对于“预测一个特定用户在特定的裂变促销下是否会转化”这个问题来说,极端随机森林测试F1分数,要高于决策树和树的Bagging,但是低于随机森林算法。
|
||
|
||
最后,我们可以把上述各个集成学习算法的得分,都显示在一张图中,来比较一下它们在这个问题上的优劣。
|
||
|
||
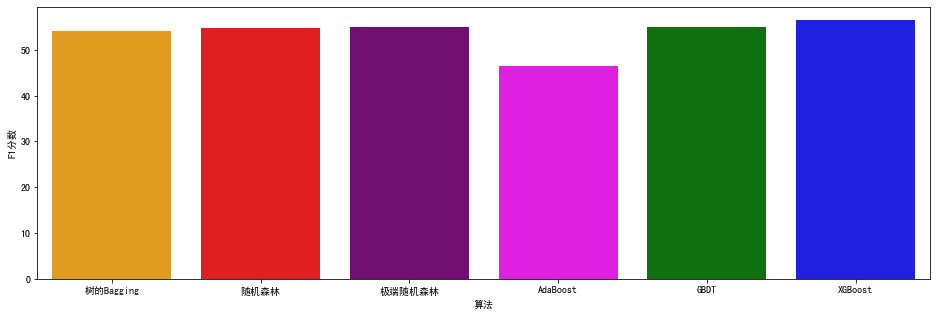
|
||
|
||
图中可以看出,对于这个问题,XGBoost、随机森林和极端随机森林,都是比较好的选择。
|
||
|
||
## 总结一下
|
||
|
||
好,到这里,我们关于集成学习的介绍就结束了,我们来做个总结。
|
||
|
||
集成学习模型是将多种同质或者异质的模型集成组合在一起,来形成更优的模型。而在这个过程的目标就是,减少机器学习模型的方差和偏差,找到机器学习模型在欠拟合和过拟合之间的最佳平衡点。
|
||
|
||
那么,怎么降低偏差呢?我们可以用Boosting方法,把梯度下降的思想应用在机器学习算法的优化上,使弱模型对数据的拟合逐渐增强。Boosting也常应用于决策树算法上,其中的GBDT 和XGBoost算法都非常受欢迎。
|
||
|
||
那怎么降低方差呢?这就要借助Bagging方法了。Bagging方法通常基于决策树,在随机生成数据集上训练出各种各样不同的树。其中的随机森林算法是在树分叉时,增加了对特征选择的随机性。随机森林在很多问题上都是一个很强的算法。我们可以把它作为一个基准,如果找到了比随机森林还优秀的模型,你就可以很欣慰了。
|
||
|
||
那么最后,如果让我在集成学习家族的算法里,给你推荐两种常用且效果好的算法,基于我个人的经验,我会觉得XGBoost、GBDT和随机森林是优于其它几种的。
|
||
|
||
## 思考题
|
||
|
||
好,在这一讲的最后,我给你留3个思考题:
|
||
|
||
1. 我在使用这些集成学习算法时,都只使用了默认参数,请你用GridSearchCV进行参数的网格搜索,找出针对这个问题更优的参数,训练出更好的模型;
|
||
2. 请你绘出上述各个算法的混淆矩阵;
|
||
3. 请你使用深度神经网络解决这个问题,看看是深层网络的性能好,还是集成学习的性能好?
|
||
|
||
欢迎你在留言区和我分享你的观点,如果你认为这节课的内容有收获,也欢迎把它分享给你的朋友,我们下一讲再见!
|
||
|
||

|
||
|