|
|
# 14 | 如何在深度学习中运用数值代数的迭代法做训练?
|
|
|
|
|
|
你好,我是朱维刚。欢迎你继续跟我学习线性代数,今天我要讲的内容是“数值线性代数的迭代法,以及如何在实践中运用迭代法求解线性方程组”。
|
|
|
|
|
|
大密度线性方程组的计算已经成为了世界上最快计算机的测试标准。2008年,IBM为美国能源部Los Alamos国家实验室建造了“Roadrunner”计算机系统,它的运算速度达到了1.026 petaflop/s(千万亿次/秒,petaflop是衡量计算机性能的一个重要单位,1 petaflop等于每秒钟进行1千万亿次的数学运算)。按摩尔定律计算,现在世界上最快的计算机已经达到了200 petaflop,我国也早就进入了世界前列,并有望实现1 exaflop/s(百亿亿次/秒),成为世界第一。
|
|
|
|
|
|

|
|
|
|
|
|
可能你会有些疑惑,为什么我要在课程后期来讲数值线性代数呢?
|
|
|
|
|
|
那是因为数值线性代数是一门特殊的学科,是特别为计算机上进行线性代数计算服务的,可以说它是研究矩阵运算算法的学科,偏向算法实践与工程设计。有了之前基础知识的铺垫后,学习数值线性代数会更有效,而且它是可以直接运用在计算机科学中的,比如:在图像压缩中,使用奇异值分解(SVD)来节省内存;在深度学习中,使用共轭梯度来加速神经网络的收敛。
|
|
|
|
|
|
## 迭代方法说明
|
|
|
|
|
|
课程内容的前期一直都在用**直接法**来解线性方程组,比如高斯消元法。但在实践中,我们在面对复杂场景时,更多的会使用**迭代法**来求解(也就是所谓的间接法),因为很多场景会用到大型稀疏矩阵。所以,我打算在这里讲讲机器学习中的迭代法应用。这里需要注意,不是说直接法不重要,直接法解决了许多相对简单的问题,也是其他方法的基础。
|
|
|
|
|
|
现在我就来说一说什么是迭代法?
|
|
|
|
|
|
我们还是通过线性方程组$Ax=b$来看看。在这里我们分解$A$,使得$A=S-T$,代入等式后得出:$Sx=Tx+b$(等式①)。
|
|
|
|
|
|
按这样的方式持续下去,通过迭代的方式来解$Sx$。这就类似于把复杂问题层层分解和简化,最终使得这个迭代等式成立:$Sx\_{k+1}=Tx\_{k}+b$(等式②)。
|
|
|
|
|
|
更具体一点来说,我们其实是从$x\_{0}$开始,解$Sx\_{1}=Tx\_{0}+b$。然后,继续解$Sx\_{2}=Tx\_{1}+b$。一直到$x\_{k+1}$非常接近$x\_{k}$时,又或者说残余值$r\_{k}=b-Ax\_{k}$接近$0$时,迭代停止。由于线性方程组的复杂程度不同,这个过程经历几百次的迭代都是有可能的。所以,迭代法的目标就是**比消元法更快速地逼近真实解**。
|
|
|
|
|
|
那么究竟应该如何快速地逼近真实解呢?
|
|
|
|
|
|
这里,$A=S-T$,$A$的分解成了关键,也就是说$A$的分解目标是**每步的运算速度和收敛速度都要快**。每步的运算速度取决于$S$,而收敛速度取决于“错误”(error),$e\_{k}$,这里的错误 $e\_{k}$是$x-x\_{k}$,也就是说$x$和$x\_{k}$的差应该快速逼近0,我们把错误表示成这样:$e\_{k+1}=S^{-1}Te\_{k}$(等式③)。
|
|
|
|
|
|
它是等式②和①差后得出的结果,迭代的每一步里,错误都会被$S^{-1}T$乘,如果$S^{-1}T$越小,那逼近0的速度就更快。在极端分解情况下,$S=A$,$T=0$,那$Ax=b$又回来了,第一次迭代就能完成收敛,其中$S^{-1}T$等于0。
|
|
|
|
|
|
但是,这一次迭代的成本太高,我们回到了非迭代方式的原点。所以,你也知道,鱼和熊掌不能兼得,$S$的选择成为了关键。那我们要如何在每一次迭代的速度和快速收敛之间做出平衡呢?我给你$S$选择的几种常见方法:
|
|
|
|
|
|
1. 雅可比方法(Jacobi method):$S$取$A$的对角部分。
|
|
|
2. 高斯-赛德尔方法(Gauss-Seidel):$S$取$A$的下三角部分,包含对角。
|
|
|
3. ILU方法(Incomplete LU):$S=L$估计乘$U$估计。
|
|
|
|
|
|
## 雅可比方法实践
|
|
|
|
|
|
总体介绍了迭代法理论之后,我们就进入迭代法运用的实践环节。
|
|
|
|
|
|
首先,我们先来试试使用雅可比方法解线性方程组,雅克比迭代法是众多迭代法中比较早且较简单的一种。所以,作为迭代法的实践开篇比较合适。让我们设一个2×2的线性方程组:
|
|
|
|
|
|
$$
|
|
|
Ax=b
|
|
|
$$
|
|
|
|
|
|
$$
|
|
|
\\left\\{\\begin{array}{c}
|
|
|
2 u-v=4 \\\\\\
|
|
|
\-u+2 v=-2
|
|
|
\\end{array}\\right.
|
|
|
$$
|
|
|
|
|
|
我们很容易就能得出这个方程组的解如下。
|
|
|
|
|
|
$$
|
|
|
\\left\[\\begin{array}{l}
|
|
|
u \\\\\\
|
|
|
v
|
|
|
\\end{array}\\right\]=\\left\[\\begin{array}{l}
|
|
|
2 \\\\\\
|
|
|
0
|
|
|
\\end{array}\\right\]
|
|
|
$$
|
|
|
|
|
|
现在我们就用雅可比方法来看看怎么解这个方程组:
|
|
|
|
|
|
首先,我们把线性方程组转换成矩阵形式。
|
|
|
|
|
|
$$
|
|
|
\\left\[\\begin{array}{cc}
|
|
|
2 & -1 \\\\\\
|
|
|
\-1 & 2
|
|
|
\\end{array}\\right\]=\\left\[\\begin{array}{c}
|
|
|
4 \\\\\\
|
|
|
\-2
|
|
|
\\end{array}\\right\]
|
|
|
$$
|
|
|
|
|
|
接着,把A的对角线放在等式左边,得出$S$矩阵。
|
|
|
|
|
|
$$
|
|
|
S=\\left\[\\begin{array}{ll}
|
|
|
2 & 0 \\\\\\
|
|
|
0 & 2
|
|
|
\\end{array}\\right\]
|
|
|
$$
|
|
|
|
|
|
其余部分移到等式右边,得出$T$矩阵。
|
|
|
|
|
|
$$
|
|
|
T=\\left\[\\begin{array}{ll}
|
|
|
0 & 1 \\\\\\
|
|
|
1 & 0
|
|
|
\\end{array}\\right\]
|
|
|
$$
|
|
|
|
|
|
于是,雅可比迭代就可以表示成下面这样的形式。
|
|
|
|
|
|
$$
|
|
|
\\mathrm{S} x\_{k+1}=T x\_{k}+\\mathrm{b}
|
|
|
$$
|
|
|
|
|
|
$$
|
|
|
\\left\\{\\begin{array}{l}
|
|
|
2 u\_{k+1}=v\_{k}+4 \\\\\\
|
|
|
2 v\_{k+1}=u\_{k}-2
|
|
|
\\end{array}\\right.
|
|
|
$$
|
|
|
|
|
|
现在是时候进行迭代了,我们从$u\_{0}=v\_{0}=0$开始。
|
|
|
|
|
|
$$
|
|
|
\\left\[\\begin{array}{l}
|
|
|
u\_{0} \\\\\\
|
|
|
v\_{0}
|
|
|
\\end{array}\\right\]=\\left\[\\begin{array}{l}
|
|
|
0 \\\\\\
|
|
|
0
|
|
|
\\end{array}\\right\]
|
|
|
$$
|
|
|
|
|
|
第一次迭代后,我们得到:
|
|
|
|
|
|
$$
|
|
|
\\left\[\\begin{array}{l}
|
|
|
u\_{1} \\\\\\
|
|
|
v\_{1}
|
|
|
\\end{array}\\right\]=\\left\[\\begin{array}{c}
|
|
|
2 \\\\\\
|
|
|
\-1
|
|
|
\\end{array}\\right\]
|
|
|
$$
|
|
|
|
|
|
第二次迭代后得到:
|
|
|
|
|
|
$$
|
|
|
\\left\[\\begin{array}{l}
|
|
|
u\_{2} \\\\\\
|
|
|
v\_{2}
|
|
|
\\end{array}\\right\]=\\left\[\\begin{array}{l}
|
|
|
\\frac{3}{2} \\\\\\
|
|
|
0
|
|
|
\\end{array}\\right\]
|
|
|
$$
|
|
|
|
|
|
第三次迭代后得到:
|
|
|
|
|
|
$$
|
|
|
\\left\[\\begin{array}{l}
|
|
|
u\_{3} \\\\\\
|
|
|
v\_{3}
|
|
|
\\end{array}\\right\]=\\left\[\\begin{array}{c}
|
|
|
2 \\\\\\
|
|
|
\-\\frac{1}{4}
|
|
|
\\end{array}\\right\]
|
|
|
$$
|
|
|
|
|
|
第四次迭代后得到:
|
|
|
|
|
|
$$
|
|
|
\\left\[\\begin{array}{l}
|
|
|
u\_{4} \\\\\\
|
|
|
v\_{4}
|
|
|
\\end{array}\\right\]=\\left\[\\begin{array}{l}
|
|
|
\\frac{15}{8} \\\\\\
|
|
|
0
|
|
|
\\end{array}\\right\]
|
|
|
$$
|
|
|
|
|
|
第五次迭代后,我们得到:
|
|
|
|
|
|
$$
|
|
|
\\left\[\\begin{array}{l}
|
|
|
u\_{5} \\\\\\
|
|
|
v\_{5}
|
|
|
\\end{array}\\right\]=\\left\[\\begin{array}{c}
|
|
|
2 \\\\\\
|
|
|
\-\\frac{1}{16}
|
|
|
\\end{array}\\right\]
|
|
|
$$
|
|
|
|
|
|
经过五次迭代后发现收敛,因为它的结果接近真实解。
|
|
|
|
|
|
$$
|
|
|
真实解
|
|
|
\\left\[\\begin{array}{l}
|
|
|
2 \\\\\\
|
|
|
0
|
|
|
\\end{array}\\right\]
|
|
|
$$
|
|
|
|
|
|
现在,再来看一下错误等式,$\\mathrm{Se}_{k+1}=T e_{k}$,我们把$S$和$T$代入等式,得出:
|
|
|
|
|
|
$$
|
|
|
\\left\[\\begin{array}{ll}
|
|
|
2 & 0 \\\\\\
|
|
|
0 & 2
|
|
|
\\end{array}\\right\] e\_{k+1}=\\left\[\\begin{array}{ll}
|
|
|
0 & 1 \\\\\\
|
|
|
1 & 0
|
|
|
\\end{array}\\right\] e\_{k}
|
|
|
$$
|
|
|
|
|
|
计算$S$的逆矩阵和$T$相乘$S^{-1}T$得出:
|
|
|
|
|
|
$$
|
|
|
e\_{k+1}=\\left\[\\begin{array}{cc}
|
|
|
0 & \\frac{1}{2} \\\\\\
|
|
|
\\frac{1}{2} & 0
|
|
|
\\end{array}\\right\] e\_{k}
|
|
|
$$
|
|
|
|
|
|
这里,$S$的逆矩阵和T相乘$S^{-1}T$有特征值$\\frac{1}{2}$和$-\\frac{1}{2}$,所以,它的谱半径是$\\rho(B)=\\frac{1}{2}$。这里的**谱半径**是用来控制收敛的,所以非常重要。谱半径从数学定义上是:矩阵(或者有界线性算子的谱半径)是指其特征值绝对值集合的上确界。这个概念是不是很难理解?具体谱半径的概念你可以查互联网来获取,为了方便你理解,这里我还是用数学方法来简单表达一下。
|
|
|
|
|
|
$$
|
|
|
B=S^{-1} T=\\left\[\\begin{array}{ll}
|
|
|
0 & \\frac{1}{2} \\\\\\
|
|
|
\\frac{1}{2} & 0
|
|
|
\\end{array}\\right\]
|
|
|
$$
|
|
|
|
|
|
通过$S$的逆矩阵和$T$相乘$S^{-1}T$,我们得到:$|\\lambda|\_{\\max }=\\frac{1}{2}$,以及:
|
|
|
|
|
|
$$
|
|
|
\\left\[\\begin{array}{cc}
|
|
|
0 & \\frac{1}{2} \\\\\\
|
|
|
\\frac{1}{2} & 0
|
|
|
\\end{array}\\right\]^{2}=\\left\[\\begin{array}{cc}
|
|
|
\\frac{1}{4} & 0 \\\\\\
|
|
|
0 & \\frac{1}{4}
|
|
|
\\end{array}\\right\]
|
|
|
$$
|
|
|
|
|
|
这里的特征值$\\frac{1}{2}$非常小,所以10次迭代后,错误就很低了,即$\\frac{1^{10}}{2}=\\frac{1}{1024}$。而如果特征值是0.99或者0.999,那很显然迭代次数就要多得多,也就是说需要更多时间来做运算。
|
|
|
|
|
|
## 高斯-赛德尔方法实践
|
|
|
|
|
|
现在我们再来看下高斯-赛德尔方法,高斯-赛德尔迭代可以**节约存储**和**加速迭代**,每迭代一次只需一组存储单元,而雅可比迭代需要两组单元。
|
|
|
|
|
|
$S$取$A$的下三角部分,还是使用之前雅可比方法中的例子,我们得出方程组:
|
|
|
|
|
|
$$
|
|
|
\\left\\{\\begin{array}{c}
|
|
|
u\_{k+1}=\\frac{1}{2} v\_{k}+2 \\\\\\
|
|
|
v\_{k+1}=\\frac{1}{2} u\_{k+1}-1
|
|
|
\\end{array}\\right.
|
|
|
$$
|
|
|
|
|
|
这里有一个比较大的变化,那就是$u\_{k}$消失了,通过$v\_{k}$,我们可以直接得到$u\_{k+1}$和$v\_{k+1}$,这样有什么好处呢?两大好处是显而易见的,就是**节约存储**和**加速迭代**。
|
|
|
|
|
|
接下来,我们从$u\_{0}=0$,$v\_{0}=-1$来测试一下迭代。
|
|
|
|
|
|
第一次迭代后,我们得到:
|
|
|
|
|
|
$$
|
|
|
\\left\[\\begin{array}{l}
|
|
|
u\_{1} \\\\\\
|
|
|
v\_{1}
|
|
|
\\end{array}\\right\]=\\left\[\\begin{array}{c}
|
|
|
\\frac{3}{2} \\\\\\
|
|
|
\\frac{-1}{4}
|
|
|
\\end{array}\\right\]
|
|
|
$$
|
|
|
|
|
|
第二次迭代后得到:
|
|
|
|
|
|
$$
|
|
|
\\left\[\\begin{array}{l}
|
|
|
u\_{2} \\\\\\
|
|
|
v\_{2}
|
|
|
\\end{array}\\right\]=\\left\[\\begin{array}{l}
|
|
|
\\frac{15}{8} \\\\\\
|
|
|
\\frac{-1}{16}
|
|
|
\\end{array}\\right\]
|
|
|
$$
|
|
|
|
|
|
第三次迭代后得到:
|
|
|
|
|
|
$$
|
|
|
\\left\[\\begin{array}{l}
|
|
|
u\_{3} \\\\\\
|
|
|
v\_{3}
|
|
|
\\end{array}\\right\]=\\left\[\\begin{array}{r}
|
|
|
\\frac{63}{32} \\\\\\
|
|
|
\-\\frac{1}{64}
|
|
|
\\end{array}\\right\]
|
|
|
$$
|
|
|
|
|
|
经过三次迭代后发现收敛,因为第三次迭代后的结果接近真实解。
|
|
|
|
|
|
错误经过计算分别是$-1, \\frac{-1}{4}, \\frac{-1}{16}, \\frac{-1}{64}$,和刚才使用雅可比方法得出的错误$2, \\frac{1}{2}, \\frac{1}{8}, \\frac{1}{32}$。比较后我们可以发现,无论是迭代次数还是收敛速度方面,高斯-赛德尔方法比雅可比方法速度快、精确度也高得多。
|
|
|
|
|
|
## 逐次超松弛方法
|
|
|
|
|
|
最后,我们在高斯-赛德尔方法上做个小调整,在迭代中引入一个参数“omega”,$ω$,即超松弛因子。然后选择一个合适的$ω$,使得$S^{-1}T$的谱半径尽可能小,这个方法就叫做逐次超松弛方法(Successive over-relaxation method,简称SOR)。
|
|
|
|
|
|
SOR方法的方程是:$ωAx=ωb$,矩阵$S$有$A$的对角线,对角线下是$ωA$,等式右边$T$是$S-ωA$,于是,我们还是使用之前雅可比方法中的例子,得到SOR方程组如下。
|
|
|
|
|
|
$$\\left\\{\\begin{array}{c}
|
|
|
2 u\_{k+1}=(2-2 \\omega) u\_{k}+\\omega v\_{k}+4 \\omega \\\\\\
|
|
|
\-\\omega u\_{k+1}+2 v\_{k+1}=(2-2 \\omega) v\_{k}-2 \\omega
|
|
|
\\end{array}\\right.$$
|
|
|
|
|
|
是不是看起来更复杂了?
|
|
|
|
|
|
没关系,其实它只是在我们眼中看起来复杂,对计算机来说是没区别的。对SOR来说,只是多了一个$ω$,而$ω$选择越好就越快。具体$ω$的选择,以及迭代的过程就不赘述了,我给你一个小提示,你可以在“$ω$大于1”和“$ω$小于1”两种情况下来多选择几个$ω$进行尝试,最后你应该会得到结论:
|
|
|
|
|
|
1. 在$ω$大于1时,$ω$越大,迭代的次数就越多,收敛速度就越慢,$ω$接近1时,迭代的次数越小,收敛速度越快。
|
|
|
2. 在$ω$小于1时,$ω$越小,迭代的次数就越多,收敛速度就越慢,$ω$接近1时,迭代的次数越小,收敛速度越快。
|
|
|
|
|
|
所以,SOR迭代法的关键就是$ω$的选择,它可以被看作是高斯-赛德尔法的扩充。
|
|
|
|
|
|
雅可比法、高斯-赛德尔法,以及SOR迭代法都是定常迭代法。接下来我讲一下和定常迭代法不同的另一类方法,也是实践中用的比较多的方法——**共轭梯度法**(Conjugate gradient),它属于Krylov子空间方法。简单来说,Krylov子空间方法是一种 “降维打击” 手段,是一种牺牲精度换取速度的方法。
|
|
|
|
|
|
## 共轭梯度法
|
|
|
|
|
|
要讲共轭梯度法,我们要先解释一下“共轭”,共轭就是按一定的规律相配的一对,通俗点说就是孪生。“轭”是牛拉车用的木头,那什么是共轭关系呢?同时拉一辆车的两头牛,就是共轭关系。
|
|
|
|
|
|

|
|
|
|
|
|
我们根据这个定义再来解释一下共轭方向,向量$p, q \\in R$, 若满足条件$pAq=0$, 则称$p$和$q$关于$A$是共轭方向,或者$p$和$q$关于$A$共轭。有了共轭和共轭方向的概念后,再来看共轭梯度法就简单多了。共轭梯度法的出现不仅是为了解决梯度下降法的收敛速度慢,而且也避免了牛顿法需要存储和计算黑塞矩阵(Hessian Matrix)并求逆的缺点。
|
|
|
|
|
|
现在来看看共轭梯度算法,设$Ax=b$,其中$A$是一个实对称正定矩阵。
|
|
|
|
|
|
首先,我们设初始值$x\_{0}$为$0$或者一个估计值,来计算$r\_{0}:=b-A x\_{0}$。如果$r\_{0}$非常小,那$x\_{0}$就是结果,如果不是就继续。
|
|
|
|
|
|
接下来设$p\_{0}:=r\_{0}$,$k:=0$。现在我们开始迭代循环。
|
|
|
|
|
|
a.计算$\\alpha\_{k}$ 。
|
|
|
|
|
|
$$\\alpha\_{k}:=\\frac{r\_{k}^{T} r\_{k}}{p\_{k}^{T} A p\_{k}}$$
|
|
|
|
|
|
b.计算$x\_{k+1}$ 。
|
|
|
|
|
|
$$x\_{k+1}:=x\_{k}+\\alpha\_{k} p\_{k}$$
|
|
|
|
|
|
c.计算$r\_{k+1}$。
|
|
|
|
|
|
$$r\_{k+1}:=r\_{k}-\\alpha\_{k} A p\_{k}$$
|
|
|
|
|
|
d.如果$r\_{k+1}$非常小,循环结束,如果不是就继续。
|
|
|
|
|
|
e.计算$β\_{k}$ 。
|
|
|
|
|
|
$$\\beta\_{k}:=\\frac{r\_{k+1}^{T} r\_{k+1}}{r\_{k}^{T} r\_{k}}$$
|
|
|
|
|
|
f.计算$p\_{k+1}$ 。
|
|
|
|
|
|
$$p\_{k+1}:=r\_{k+1}+\\beta\_{k} p\_{k}$$
|
|
|
|
|
|
g.$k:=k+1$。
|
|
|
|
|
|
4. 返回结果$x\_{k+1}$。
|
|
|
|
|
|
从算法中我们可以看出,共轭梯度法的优点是**存储量小**和**具有步收敛性**。如果你熟悉MATLAB,就会发现共轭梯度法的实现超级简单,只需要短短十几行代码(下方代码来自于MATLAB/GNU Octave的例子)。
|
|
|
|
|
|
```
|
|
|
function x = conjgrad(A, b, x)
|
|
|
r = b - A * x;
|
|
|
p = r;
|
|
|
rsold = r' * r;
|
|
|
|
|
|
|
|
|
for i = 1:length(b)
|
|
|
Ap = A * p;
|
|
|
alpha = rsold / (p' * Ap);
|
|
|
x = x + alpha * p;
|
|
|
r = r - alpha * Ap;
|
|
|
rsnew = r' * r;
|
|
|
if sqrt(rsnew) < 1e-10
|
|
|
break;
|
|
|
end
|
|
|
p = r + (rsnew / rsold) * p;
|
|
|
rsold = rsnew;
|
|
|
end
|
|
|
end
|
|
|
|
|
|
```
|
|
|
|
|
|
## 机器学习中的共轭梯度
|
|
|
|
|
|
共轭梯度法经常被用在训练神经网络中,在实践中已经证明,它是比**梯度下降**更有效的方法,因为就像刚才讲的,它不需要计算黑塞矩阵。那我现在就来讲一讲,使用共轭梯度法的神经网络训练过程。
|
|
|
|
|
|
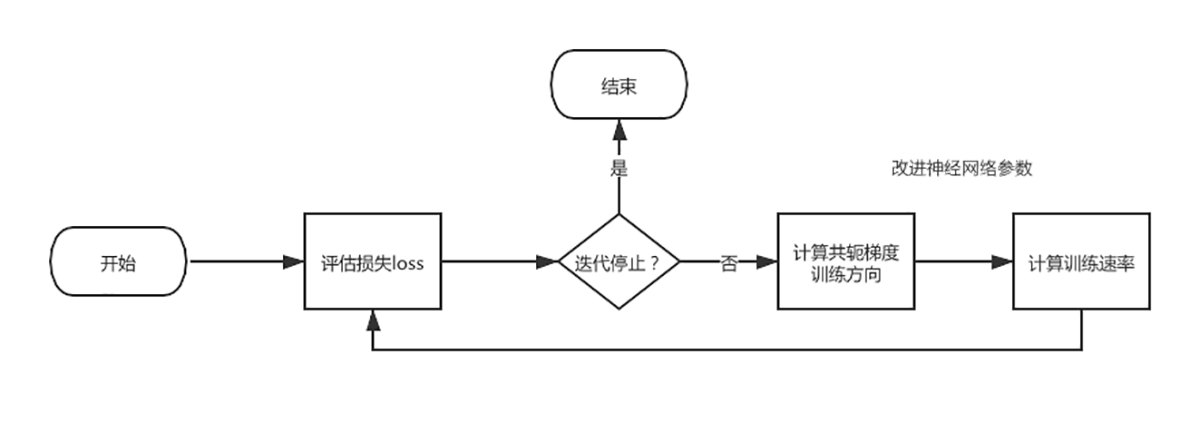
|
|
|
|
|
|
在整个训练过程中,**参数改进**是重点,当然这也是所有神经网络训练的重点。这个过程是通过计算共轭梯度的训练方向,然后计算训练速率来实现的。在共轭梯度训练算法中,搜索是按共轭方向进行的,也就是说,训练方向是共轭的。所以,收敛速度比梯度下降要快。
|
|
|
|
|
|
现在我们来看训练方向的计算方法。首先,我们设置训练方向向量为$d$,然后,定义一个初始参数向量$w^{0}$,以及一个初始训练方向向量$d^{0}=-g^{0}$,于是,共轭梯度法构造出的训练方向可以表示成:$d^{i+1}=g^{i+1}+d^{i} \\cdot \\gamma^{i}$。
|
|
|
|
|
|
其中,$g$是梯度向量,$γ$是共轭参数。参数通过这个表达式来更新和优化。通常训练速率$\\eta$可使用单变量函数优化方法求得。
|
|
|
|
|
|
$$w^{i+1}=w^{i}+d^{i} \\cdot \\eta^{i}$$
|
|
|
|
|
|
## 本节小结
|
|
|
|
|
|
好了,到这里数值线性代数的迭代法这一讲就结束了,最后我再总结一下前面讲解的内容。
|
|
|
|
|
|
首先,我先解释了数值线性代数,接着再整体讲解了迭代方法。然后,举了一个线性方程组的例子,运用迭代法中的几个比较著名的实践方法:雅可比方法、高斯-赛德尔方法,以及逐次超松弛方法,来解这个线性方程组。最后,我把共轭梯度法用在了深度学习的神经网络训练中。
|
|
|
|
|
|
希望你能在了解了数值线性代数,以及迭代法后,更多地在计算机科学领域中,运用迭代法做矩阵运算。如果有兴趣,你也可以学习其它在实践中使用的迭代法。
|
|
|
|
|
|
## 线性代数练习场
|
|
|
|
|
|
练习时刻到了,这次继续使用第一篇线性方程组里的例子,你可以挑选任意一个迭代法来求解这个线性方程组。
|
|
|
|
|
|
假设,一个旅游团由孩子和大人组成,去程时他们一起坐大巴,每个孩子的票价3元,大人票价3.2元,总共花费118.4元。回程时一起做火车,每个孩子的票价3.5元,大人票价3.6元,总共花费135.2元。请问这个旅游团中有多少孩子和大人?
|
|
|
|
|
|
设小孩人数为$x\_{1}$,大人人数为$x\_{2}$,于是我们得到了一个方程组:
|
|
|
|
|
|
$$\\left\\{\\begin{array}{c}
|
|
|
3 x\_{1}+3.2 x\_{2}=118.4 \\\\\\
|
|
|
3.5 x\_{1}+3.6 x\_{2}=135.2
|
|
|
\\end{array}\\right.$$
|
|
|
|
|
|
这个方程组的解是:
|
|
|
|
|
|
$$\\left\\{\\begin{array}{l}
|
|
|
x\_{1}=16 \\\\\\
|
|
|
x\_{2}=22
|
|
|
\\end{array}\\right.$$
|
|
|
|
|
|
你可以计算一下多少次迭代后它能收敛,也就是逼近真实解?以及它的错误$e$又分别是多少?
|
|
|
|
|
|
欢迎在留言区晒出的你的运算过程和结果。如果有收获,也欢迎你把这篇文章分享给你的朋友。
|
|
|
|