|
|
# 08 | 线性映射:如何从坐标系角度理解两个向量空间之间的函数?
|
|
|
|
|
|
你好,我是朱维刚。欢迎你继续跟我学习线性代数,今天我们要讲的内容是“线性映射”。
|
|
|
|
|
|
前面我们学的内容都是局限在一个线性空间,或者说一个向量空间中,但今天不一样哦,我们要来看看两个向量空间之间的关系,也就是线性映射。
|
|
|
|
|
|
之前我说过,向量也是对象,是能够相加,能够被标量乘的对象,而且这样计算的结果还是向量。而**加和标量乘这样的运算同样适用线性映射**。比如:两个实数向量空间$V$和$W$,有一个函数$\\phi$来完成向量空间$V$到$W$的映射,如果我们想要同时保持向量空间结构不变,那么$\\phi$就要满足:
|
|
|
|
|
|
$$\\begin{array}{l}
|
|
|
\\phi(x+y)=\\phi(x)+\\phi(y)\\\\\\
|
|
|
\\phi(\\lambda x)=\\lambda \\phi(x)
|
|
|
\\end{array}$$
|
|
|
|
|
|
其中,所有$x$和$y$属于向量空间$V$, $λ$属于实数。于是,我们得到了线性映射的定义。
|
|
|
|
|
|
## 线性映射定义
|
|
|
|
|
|
假设有两个向量空间$V$和$W$,$\\phi$是一个函数,它完成了向量空间V到W的线性映射,那么线性映射必须满足等式:
|
|
|
|
|
|
$$\\phi(\\lambda x+\\varphi y)=\\lambda \\phi(x)+\\varphi \\phi(y)$$
|
|
|
|
|
|
其中,任意$x$和$y$都属于向量空间$V$,而任意 $λ$和$φ$都属于实数。
|
|
|
|
|
|
当然,我们能把线性映射表示成矩阵,也就是线性映射矩阵,或者叫做变换矩阵。但因为向量还能组合成矩阵的列,所以我们要特别注意区分矩阵表示的是线性映射还是向量的集合。向量的集合是静态的,而变换矩阵则是动态的哦。
|
|
|
|
|
|
接下来我们再来看看两个任意集合$V$到$W$的三类特殊映射,了解一下函数 $\\phi$在不一样的情况下究竟表达了怎样的关系。
|
|
|
|
|
|
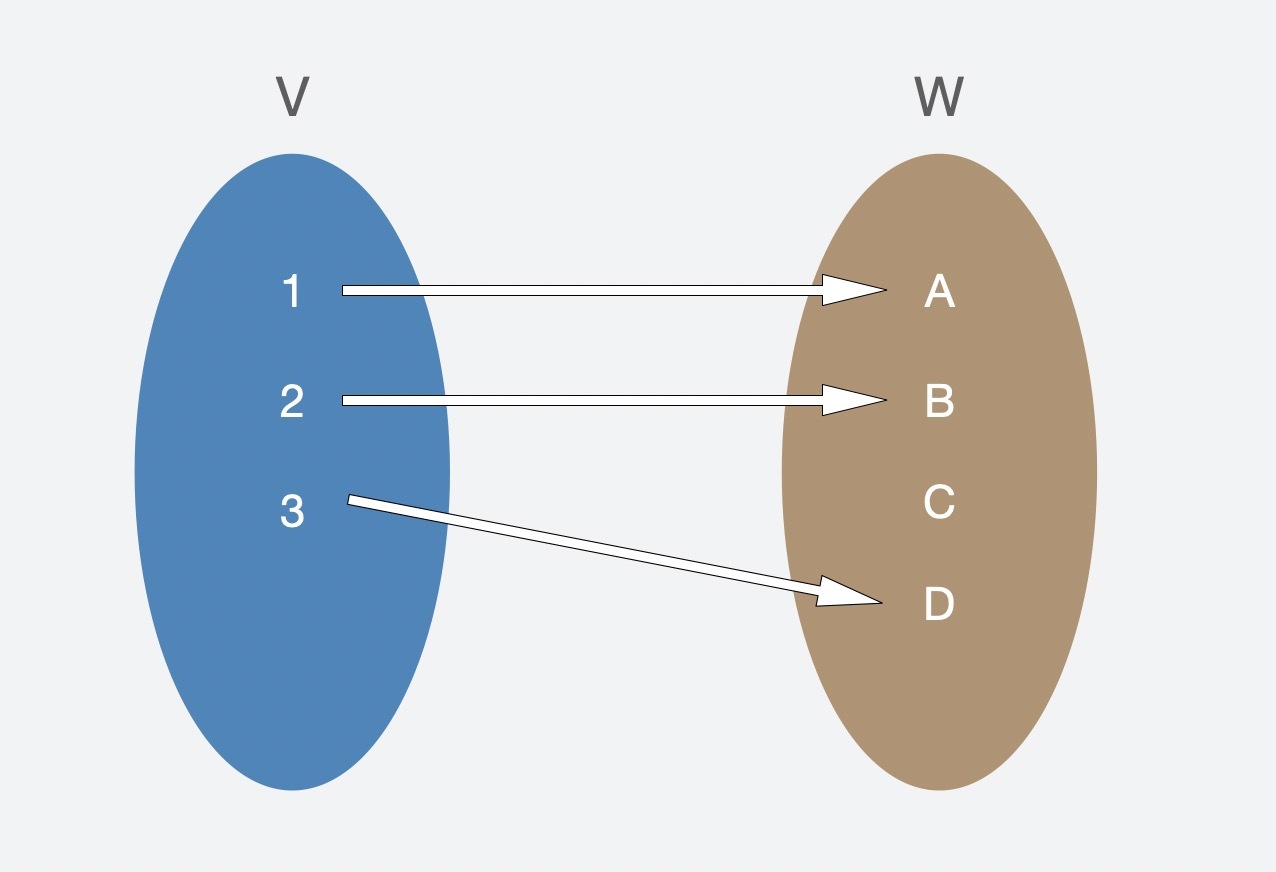
1. 函数$\\phi$是单射(Injective)时:如果 $\\phi(x)= \\phi(y)$ ,那么$x=y$ ,其中任意$x$和$y$都属于集合$V$,从图中可以看出它表达的是一对一的关系,也就是我们可以由集合$V$的一个元素唯一确定一个集合$W$的元素。
|
|
|
|
|
|
|
|
|
|
|
|
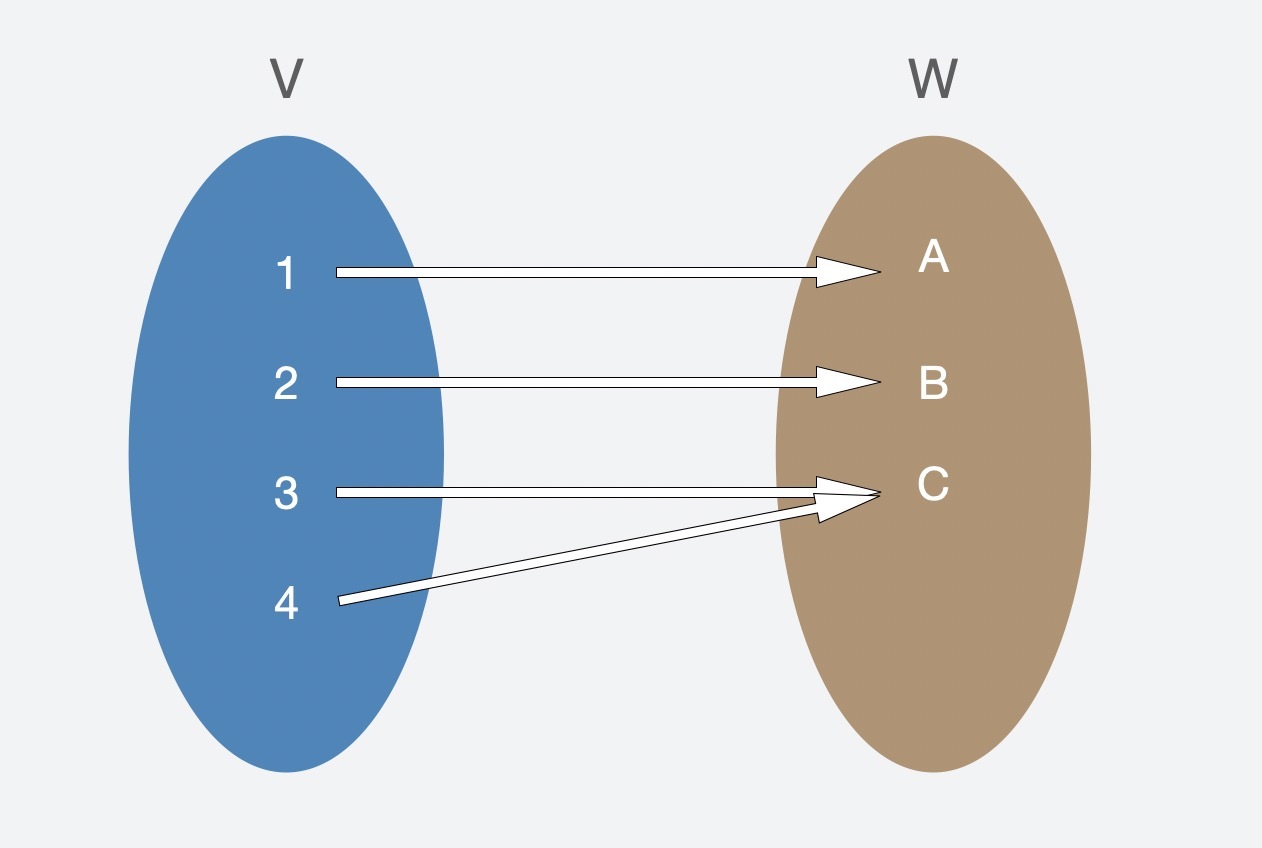
2. 函数$\\phi$是满射(Surjective):也就是满足等式 $\\phi(V)= W$,从图中我们可以看出它表达的是多对一的关系,也就是多个集合$V$的元素能够确定一个集合$W$的元素。
|
|
|
|
|
|
|
|
|
|
|
|
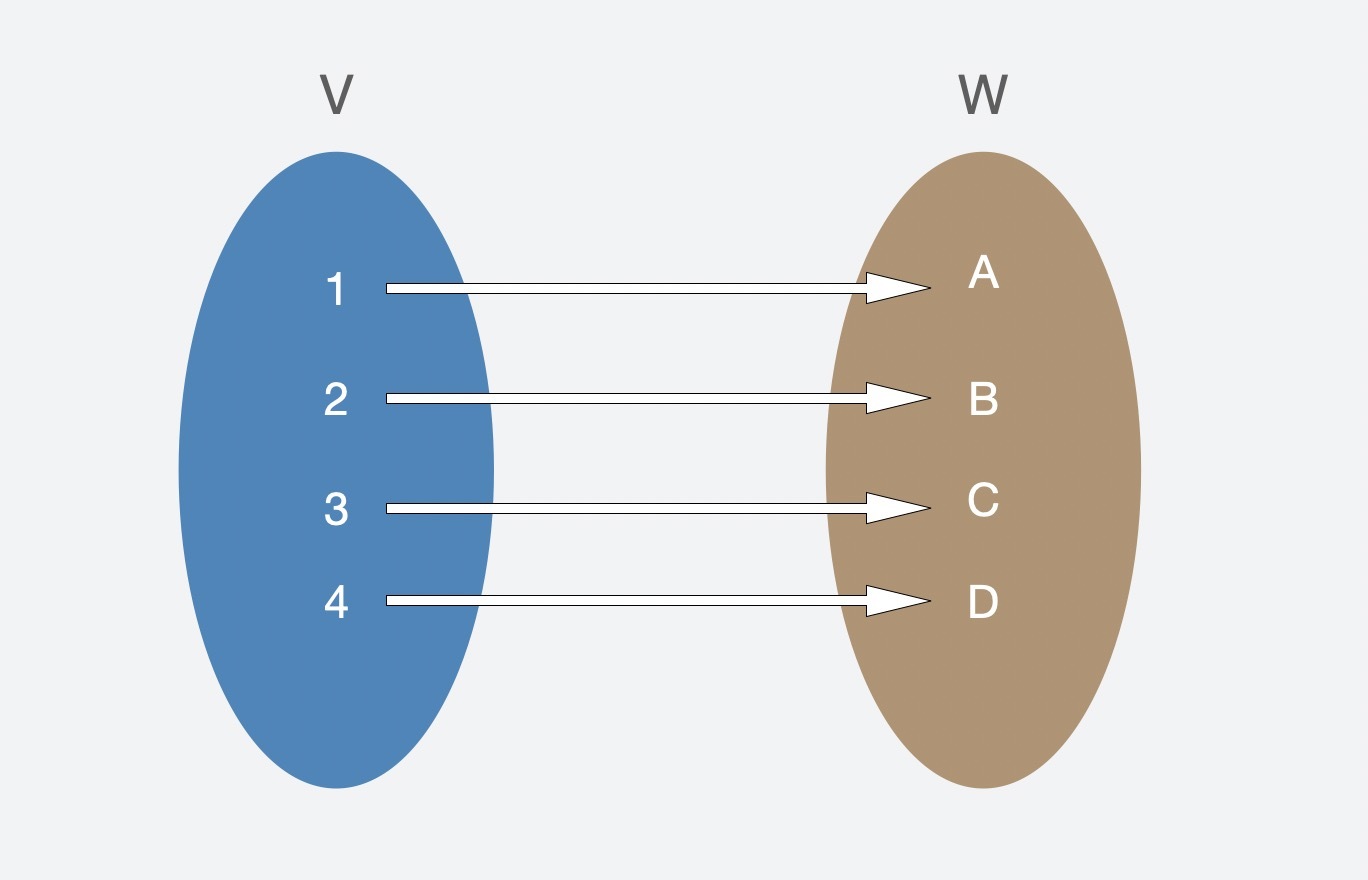
3. 函数$\\phi$是双射(Bijective),就意味着它既是单射又是满射,从图中我们可以看出,它表达的是,所有$V$集合的元素都和$W$集合的元素一一对应,不多不少。
|
|
|
|
|
|
|
|
|
通过这些定义,我们就可以引入几个线性映射的特殊概念了。
|
|
|
|
|
|
1. 同构( Isomorphism):即函数 $\\phi$使$V$到$W$是线性且双射的;
|
|
|
2. 自同态(Endomorphism):即函数 $\\phi$使$V$到$V$是线性的;
|
|
|
3. 自同构(Automorphism):即函数$\\phi$使$V$到$V$是线性且双射的;
|
|
|
4. 把$V$到$V$,元素$x$到$x$的映射定义为恒等映射。
|
|
|
|
|
|
那么,为什么你需要了解这几个特殊的概念呢?那是因为我们需要通过这些概念引出一个定理:有限维度的向量空间$V$和$W$,如果它们的维度相等,那么它们就是同构的。那就是说,同一维度的向量空间某种程度来说是一样的,因为它们能在没有发生损失的条件下互相转换。
|
|
|
|
|
|
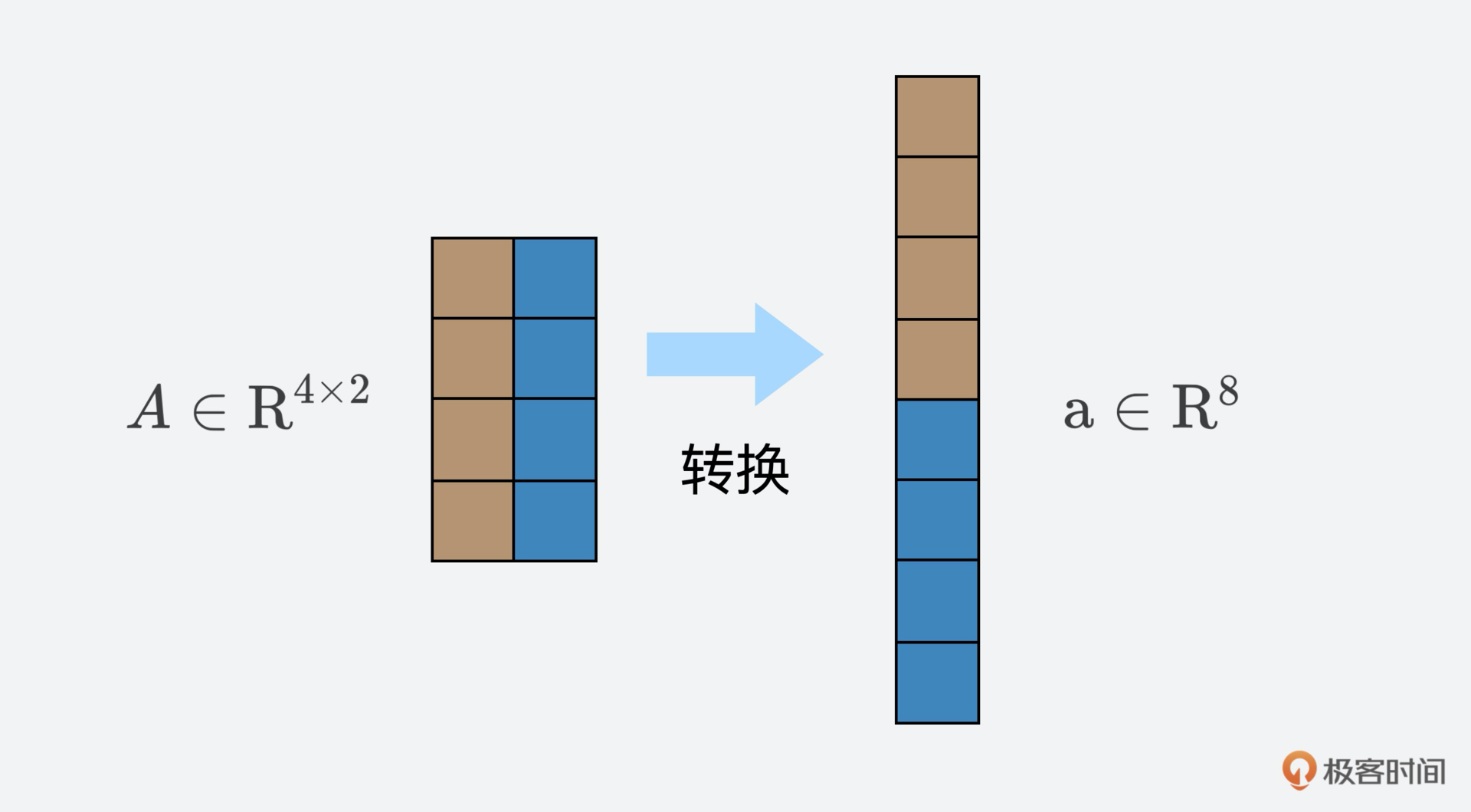
比如,$\\mathrm{R}^{m \\times n}$矩阵向量空间,和$\\mathrm{R}^{mn}$长度是$mn$的向量空间,我们可以认为它们是相同的,因为它们维度都是$mn$,而且存在一个线性映射和双射使得它们能互相转换。还记得在矩阵那节课中,我提到的矩阵转换吗?很多时候这类转换就是为了计算方便。
|
|
|
|
|
|
|
|
|
|
|
|
## 线性映射的矩阵表示
|
|
|
|
|
|
刚才提到了线性映射的矩阵表达,那在了解了线性映射的定义后,现在是时候来具体看一看这个更直观,且有实践意义的表达了。之所以说它有实践意义,那是因为我们赋予了它动态特性,让矩阵表示线性变换的过程。
|
|
|
|
|
|
如果存在一个$n$维向量空间$V$和它的一个有序基$B=(b\_{1},\\cdots,b\_{n})$,那么对于任意一个属于$V$的$x$,我们能得到一个这样的线性组合:$x=\\alpha\_{1} b\_{1}+\\cdots+\\alpha\_{n} b\_{n}$,我们可以说
|
|
|
|
|
|
$$\\alpha=\\left\[\\begin{array}{c}
|
|
|
\\alpha\_{1} \\\\\\
|
|
|
\\cdot \\\\\\
|
|
|
\\cdot \\\\\\
|
|
|
\\cdot \\\\\\
|
|
|
\\alpha\_{n}
|
|
|
\\end{array}\\right\]$$
|
|
|
|
|
|
是$x$的坐标向量或坐标表达。
|
|
|
|
|
|
我们都了解二维直角坐标系,现在我们通过一个例子,看看一个同样的向量在两个不同坐标系中的表示,加深一下你对线性映射的理解。
|
|
|
|
|
|
|
|
|
|
|
|
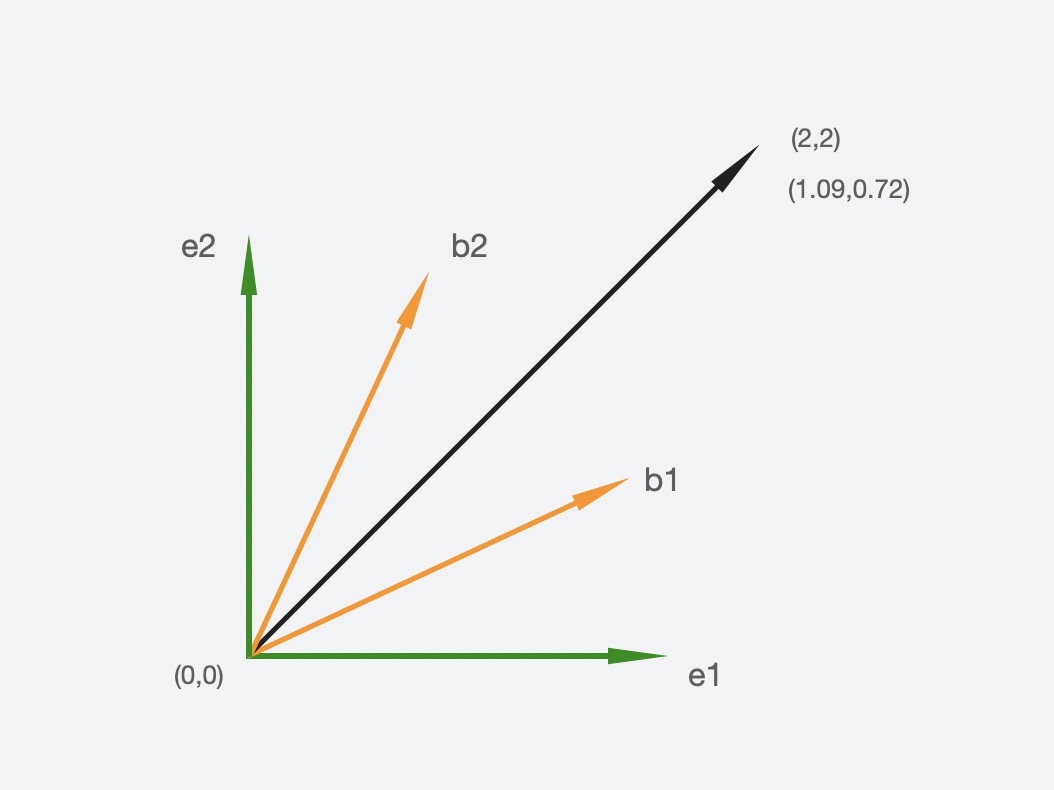
假设图中绿色是坐标系$V$,黄色是坐标系$W$。
|
|
|
|
|
|
在$V$中,$e\_{1}$和$e\_{2}$是$V$的标准基,向量$x$由线性组合$e\_{1}$和$e\_{2}$表示,$x$的坐标是(2,2),于是,$x$在$V$中可以被表示成:$x=2 e\_{1}+2 e\_{2}$。
|
|
|
|
|
|
在$W$中,$b\_{1}$和$b\_{2}$是$W$的标准基,向量$x$由线性组合$b\_{1}$和$b\_{2}$表示,而这里的$x$坐标就不同了,变成了(1.09,0.72),于是,$x$在$W$中可以被表示成:$x=1.09 b\_{1}+0.72 b\_{2}$。
|
|
|
|
|
|
说到这,你是不是对线性映射有了一个更直观的感受?现在我们就把矩阵引入到线性映射中,于是,我们就有了**变换矩阵**,也就是用矩阵表示线性变换的过程。
|
|
|
|
|
|
变换矩阵的定义是:我们有向量空间$V$和$W$,它们各自有相应的有序基 $B=(b\_{1},\\cdots,b\_{n})$和 $C=(c\_{1},\\cdots,c\_{m})$ ,而$\\phi$就是$V$到$W$的线性映射:$\\phi\\left(b\_{j}\\right)=\\alpha\_{1 j} c\_{1}+\\cdots+\\alpha\_{m j} c\_{m}$。
|
|
|
|
|
|
线性映射$\\phi$中的$j$是从$1$到$n$,于是,我们就能得到一个$\\phi$的$m \\times n$的变换矩阵 $A\_{\\phi}$,这个变换矩阵中的元素是$A\_{\\phi}(i, j)=\\alpha\_{i j}$,也就是说,$\\phi\\left(b\_{j}\\right)$的坐标就是 $A\_{\\phi}$的第$j$列。
|
|
|
|
|
|
我们可以来简化一下表达,把它表示成这样: $y=A\_{\\phi}(x)$。其中,$x$是$V$基于$B$基的坐标向量,$y$是$W$基于$C$基的坐标向量。所以,变换矩阵可以被用来在有序基上,映射坐标。
|
|
|
|
|
|
我们来看一个变换矩阵例子:已知两个向量空间$V$和$W$,它们各自相应的有序基是 $B=(b\_{1},\\cdots,b\_{3})$和 $C=(c\_{1},\\cdots,c\_{4})$ ,线性映射$\\phi$表示成以下形式。
|
|
|
|
|
|
$$\\begin{array}{l}
|
|
|
\\phi\\left(b\_{1}\\right)=c\_{1}-c\_{2}+3 c\_{3}-c\_{4} \\\\\\
|
|
|
\\phi\\left(b\_{2}\\right)=2 c\_{1}+c\_{2}+7 c\_{3}+2 c\_{4} \\\\\\
|
|
|
\\phi\\left(b\_{3}\\right)=3 c\_{2}+c\_{3}+4 c\_{4}
|
|
|
\\end{array}$$
|
|
|
|
|
|
于是,我们可以通过这些条件得到变换矩阵$A\_{\\phi}$如下。
|
|
|
|
|
|
$$ A\_{\\phi}=\\left\[\\begin{array}{ccc}
|
|
|
1 & 2 & 0 \\\\\\
|
|
|
\-1 & 1 & 3 \\\\\\
|
|
|
3 & 7 & 1 \\\\\\
|
|
|
\-1 & 2 & 4
|
|
|
\\end{array}\\right\]$$
|
|
|
|
|
|
理解到这里还不算透彻,我们要更进一步,看看在现实图形图像处理中的线性变换是什么样的。接下来我们通过下面三个图形的例子来理解一下。
|
|
|
|
|
|
|
|
|
|
|
|
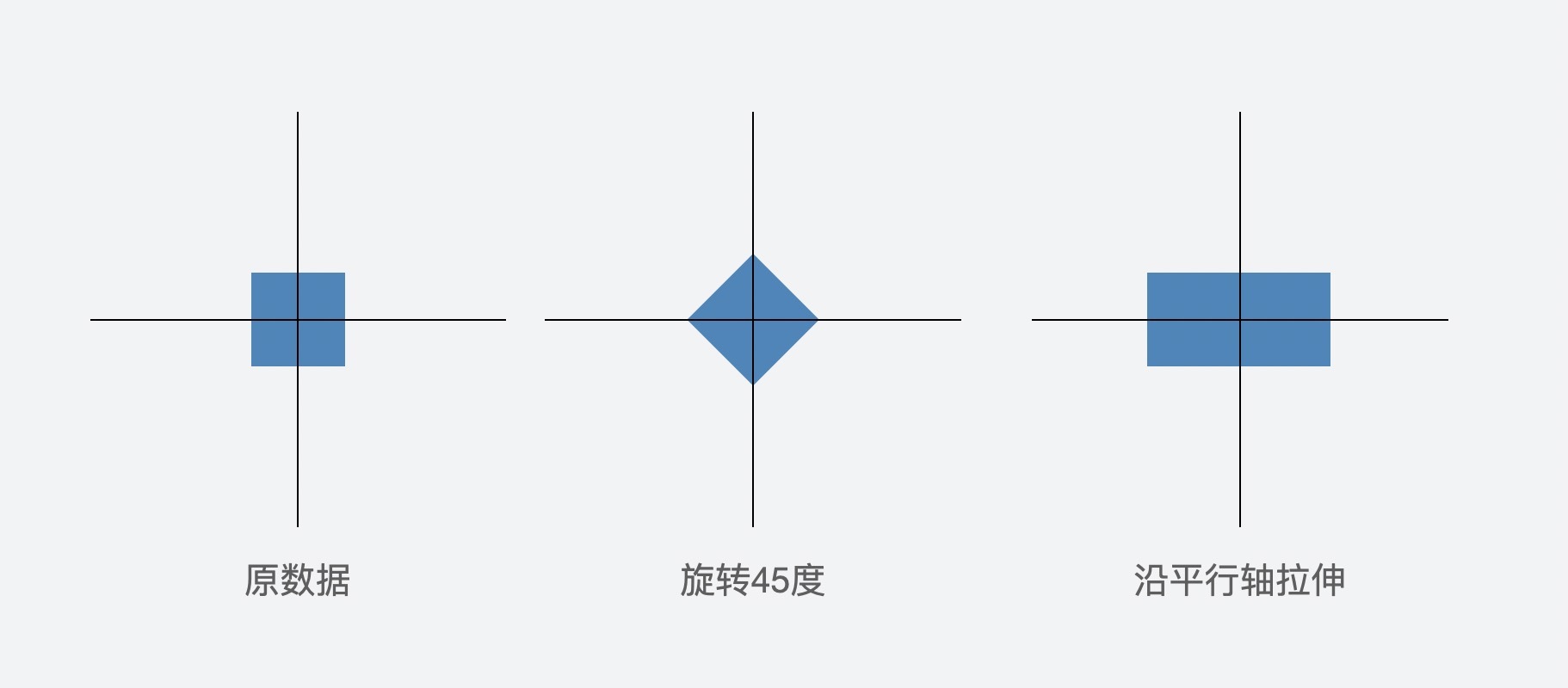
第一个图形是原始数据,你可以把它看成是由几百个向量的密集点组成的图。
|
|
|
|
|
|
第二个图形的效果看起来很简单,是由原始数据经过45度变换后得到的,它的变换矩阵是下面这样的。
|
|
|
|
|
|
$$A\_{1}=\\left\[\\begin{array}{cc}
|
|
|
\\cos \\left(\\frac{\\pi}{4}\\right) & -\\sin \\left(\\frac{\\pi}{4}\\right) \\\\\\
|
|
|
\\sin \\left(\\frac{\\pi}{4}\\right) & \\cos \\left(\\frac{\\pi}{4}\\right)
|
|
|
\\end{array}\\right\]$$
|
|
|
|
|
|
第三个图形是原始数据沿平行轴拉伸两倍的效果,变换矩阵是下面这样的。
|
|
|
|
|
|
$$A\_{2}=\\left\[\\begin{array}{cc}
|
|
|
2 & 0 \\\\\\
|
|
|
0 & 1
|
|
|
\\end{array}\\right\]$$
|
|
|
|
|
|
当然,这三个图形是比较简单的例子,是为了方便你理解,其实我们还能做更复杂的变换,比如:旋转、伸缩的组合等等。
|
|
|
|
|
|
## 基的改变
|
|
|
|
|
|
之前我们讨论的线性映射都是在**基**是一定的情况下,通过变换矩阵做线性映射。那如果基改变了呢?讨论基的改变在实践中也是有重要意义的。比如,为了最小化数据压缩损失,我们需要找到一个合适的被用来数据投影的基。
|
|
|
|
|
|
现在我们就来看看,如果我们改变向量空间$V$和$W$的基,线性映射$\\phi$的变换矩阵会如何改变。我们给向量空间$V$和$W$各自增加两个有序基:$\\widetilde{B}=\\left(\\tilde{b}\_{1}, \\ldots, \\widetilde{b}\_{n}\\right)$和$\\widetilde{C}=\\left(\\tilde{c}\_{1}, \\ldots, \\widetilde{c}\_{m}\\right)$,而 $\\tilde{A}\_{\\phi}$是基于新的有序基的变换矩阵。这样,$\\tilde{A}\_{\\phi}$变换矩阵的计算公式就是:$\\tilde{A}\_{\\phi}=T^{-1} A\_{\\phi} S$。
|
|
|
|
|
|
在这个新的公式中,$S$是 $\\mathrm{R}^{n \\times n}$向量空间$V$的恒等映射变换矩阵,向量空间$V$的恒等映射把基于$\\widetilde{B}$的坐标,映射到基于$B$的坐标上。同理,$T$是$\\mathrm{R}^{m \\times m}$向量空间$W$的恒等映射变换矩阵,向量空间$W$的恒等映射把基于$\\widetilde{C}$的坐标,映射到基于$C$的坐标上。
|
|
|
|
|
|
理论是这样的,那我们还是要通过一个例子来看一下,基改变后,新的线性映射 $\\phi$的变换矩阵到底是如何获取的。我们已知,一个三维实数向量空间$\\mathrm{R}^{3}$到四维实数向量空间$\\mathrm{R}^{4}$的一个线性映射,它们各自有标准基$B$和$C$。
|
|
|
|
|
|
$$B=\\left\\{\\left\[\\begin{array}{l}
|
|
|
1 \\\\\\
|
|
|
0 \\\\\\
|
|
|
0
|
|
|
\\end{array}\\right\],\\left\[\\begin{array}{l}
|
|
|
0 \\\\\\
|
|
|
1 \\\\\\
|
|
|
0
|
|
|
\\end{array}\\right\],\\left\[\\begin{array}{l}
|
|
|
0 \\\\\\
|
|
|
0 \\\\\\
|
|
|
1
|
|
|
\\end{array}\\right\]\\right\\}, C=\\left\\{\\left\[\\begin{array}{l}
|
|
|
1 \\\\\\
|
|
|
0 \\\\\\
|
|
|
0 \\\\\\
|
|
|
0
|
|
|
\\end{array}\\right\],\\left\[\\begin{array}{l}
|
|
|
0 \\\\\\
|
|
|
1 \\\\\\
|
|
|
0 \\\\\\
|
|
|
0
|
|
|
\\end{array}\\right\],\\left\[\\begin{array}{l}
|
|
|
0 \\\\\\
|
|
|
0 \\\\\\
|
|
|
1 \\\\\\
|
|
|
0
|
|
|
\\end{array}\\right\],\\left\[\\begin{array}{l}
|
|
|
0 \\\\\\
|
|
|
0 \\\\\\
|
|
|
0 \\\\\\
|
|
|
1
|
|
|
\\end{array}\\right\]\\right\\}$$
|
|
|
|
|
|
基于它们各自的标准基$B$和$C$,它的变换矩阵是:
|
|
|
|
|
|
$$A\_{\\phi}=\\left\[\\begin{array}{ccc}
|
|
|
1 & 2 & 0 \\\\\\
|
|
|
\-1 & 1 & 3 \\\\\\
|
|
|
3 & 7 & 1 \\\\\\
|
|
|
\-1 & 2 & 4
|
|
|
\\end{array}\\right\]$$
|
|
|
|
|
|
那么现在,我们来看一下,基$B$和$C$改变为$\\widetilde{B}$和$\\widetilde{C}$之后,会有怎样的变化。
|
|
|
|
|
|
$$\\widetilde{B}=\\left\\{\\left\[\\begin{array}{l}
|
|
|
1 \\\\\\
|
|
|
1 \\\\\\
|
|
|
0
|
|
|
\\end{array}\\right\],\\left\[\\begin{array}{l}
|
|
|
0 \\\\\\
|
|
|
1 \\\\\\
|
|
|
1
|
|
|
\\end{array}\\right\],\\left\[\\begin{array}{l}
|
|
|
1 \\\\\\
|
|
|
0 \\\\\\
|
|
|
1
|
|
|
\\end{array}\\right\]\\right\\}, \\widetilde{C}=\\left\\{\\left\[\\begin{array}{l}
|
|
|
1 \\\\\\
|
|
|
1 \\\\\\
|
|
|
0 \\\\\\
|
|
|
0
|
|
|
\\end{array}\\right\],\\left\[\\begin{array}{l}
|
|
|
1 \\\\\\
|
|
|
0 \\\\\\
|
|
|
1 \\\\\\
|
|
|
0
|
|
|
\\end{array}\\right\],\\left\[\\begin{array}{l}
|
|
|
0 \\\\\\
|
|
|
1 \\\\\\
|
|
|
1 \\\\\\
|
|
|
0
|
|
|
\\end{array}\\right\],\\left\[\\begin{array}{l}
|
|
|
1 \\\\\\
|
|
|
0 \\\\\\
|
|
|
0 \\\\\\
|
|
|
1
|
|
|
\\end{array}\\right\]\\right\\}$$
|
|
|
|
|
|
对于新基$\\widetilde{B}$和$\\widetilde{C}$,我们得到$S$和$T$:
|
|
|
|
|
|
$$S=\\left\[\\begin{array}{lll}
|
|
|
1 & 0 & 1 \\\\\\
|
|
|
1 & 1 & 0 \\\\\\
|
|
|
0 & 1 & 1
|
|
|
\\end{array}\\right\], T=\\left\[\\begin{array}{llll}
|
|
|
1 & 1 & 0 & 1 \\\\\\
|
|
|
1 & 0 & 1 & 0 \\\\\\
|
|
|
0 & 1 & 1 & 0 \\\\\\
|
|
|
0 & 0 & 0 & 1
|
|
|
\\end{array}\\right\]$$
|
|
|
|
|
|
于是,我们就可以通过公式得到想要的$\\tilde{A}\_{\\phi}$了。
|
|
|
|
|
|
$$\\tilde{A}\_{\\phi}=T^{-1} A\_{\\phi} S=\\left\[\\begin{array}{ccc}
|
|
|
\-4 & -4 & -2 \\\\\\
|
|
|
6 & 0 & 0 \\\\\\
|
|
|
4 & 8 & 4 \\\\\\
|
|
|
1 & 6 & 3
|
|
|
\\end{array}\\right\]$$
|
|
|
|
|
|
## 两个重要的子空间
|
|
|
|
|
|
最后,我再来讲两个重要的子空间——核空间和像空间,说它们重要是有原因的。核空间可以帮助我们研究线性方程组的性质,同时还可以帮助我们把复杂问题简化,也就是将复杂的大集合分解成小集合的并来研究。而像空间可以帮助我们快速得到线性方程组的秩,这样就能快速判断线性方程组解的情况。现在我们来具体了解一下。
|
|
|
|
|
|
### 核空间
|
|
|
|
|
|
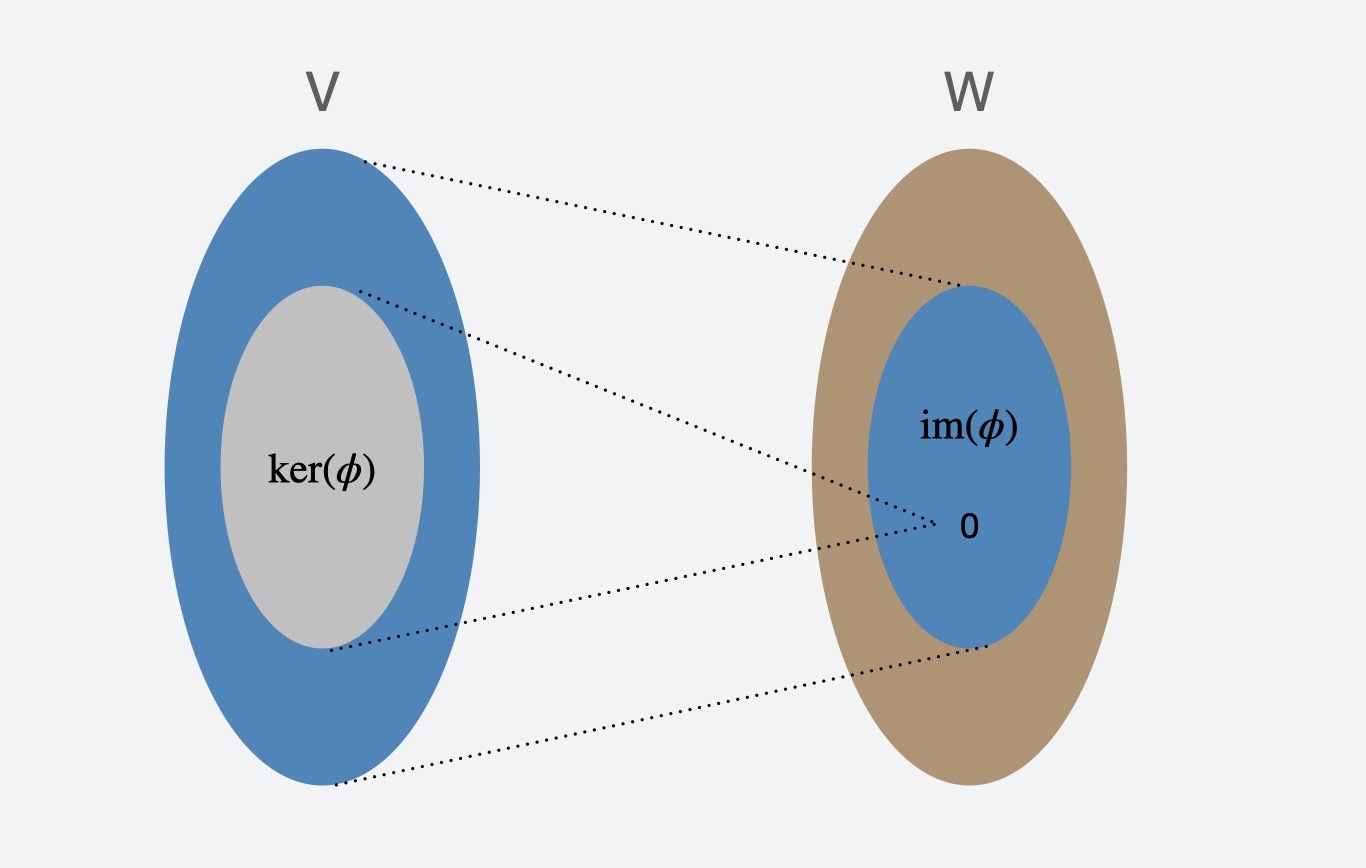
核空间也叫做零空间,你还记得$Ax=b$吗?核空间关注的就是$Ax=0$,也就是向量空间$V$中所有经过$\\phi$映射为零的向量集合,用符号表示就是:$\\operatorname{ker}(\\phi)$ 。核的维数叫做零化度(nullity),表示成:$\\operatorname{dim}(\\operatorname{ker}(\\phi))$。
|
|
|
|
|
|
### 像空间
|
|
|
|
|
|
向量空间$V$中所有经过$\\phi$映射后的向量集合,叫做像空间,用符号表示就是:$\\operatorname{im}(\\phi)$,像空间维数就是秩,表示成:$\\operatorname{rk}(\\phi)$。
|
|
|
|
|
|
通过图形表达出来,你应该能够更好地理解。
|
|
|
|
|
|
|
|
|
|
|
|
最后我以一个定理来结束本节的内容,秩-零化度定理:V的维数等于核空间维数与像空间维数之和$\\operatorname{dim}(\\mathrm{V})=\\operatorname{dim}(\\operatorname{ker}(\\phi))+\\operatorname{rk}(\\phi)$。
|
|
|
|
|
|
## 本节小结
|
|
|
|
|
|
好了,到这里线性映射这一讲就结束了,最后我再总结一下前面讲解的内容。
|
|
|
|
|
|
线性映射赋予了线性代数灵魂,也让它在计算机科学中发挥了很大的作用。线性映射的矩阵变换是这一节的重点,你要牢固掌握,因为它在无数现实场景中都在使用,比如:三维图形图像处理中的线性变换,图形的伸缩、旋转等等。
|
|
|
|
|
|
## 线性代数练习场
|
|
|
|
|
|
好,今天练习时刻到了,刚刚我们通过图形图像处理中的线性变换的例子,讲了矩阵变换。现在我们还是以这个例子为基础,不过这一次轮到你来解答问题了。如果我们把原始数据整体沿平行轴收缩两倍,那变换矩阵会是怎样的呢?
|
|
|
|
|
|
欢迎在留言区或者部落里晒出你的变换矩阵。如果你觉得有所收获,也欢迎你把这篇文章分享给你的朋友。
|
|
|
|