7.6 KiB
开篇词 | 从今天起,学会线性代数
你好,我是朱维刚。欢迎你跟我一起重学线性代数!
我们为什么要学线性代数?
“数学”其实是一个老生常谈的话题。我出生在80年代,在我这一代,父母一直给我们灌输“学好数理化,走遍天下都不怕”的思想。我们每个人都是从很小的时候就开始学习数学了。那你有没有想过,学了那么多年数学,我们到底把这些数学知识都学到哪里去了呢?它们到底可以用在什么地方呢?
我自己对数学这个学科比较感兴趣,从小就在想这些问题,但是一直百思不得其解。一直到了大学和研究生阶段,学了工程数学之后,我才真正恍然大悟——原来数学可以用在各类工程上,比如我现在正在从事的人工智能中的机器学习项目。
说起来,我与机器学习结缘还是比较早的。
2006年年初,我开始接触机器学习,加入了IronPort(后来被思科收购了)公司的TDA(Threat Data Analyst)团队。当时公司的主要业务集中在“反垃圾邮件”这个领域,我们这些工程师的主要职责,就是每天分析全球大量邮件数据、人工打分类标签、写匹配规则来优化机器学习引擎。其实有点类似如今的数据分析师和数据科学家,可以说基本上每天都在跟“数学”打交道。如今14年过去了,目前我致力于建筑行业数字孪生的工作,我希望通过人工智能技术,推动建筑行业进入“智慧建造”时代。
做了这么多年机器学习,我经常听到有人跟我说,机器学习很难啊,你到底是怎么学会的?
其实,我想说,机器学习本身没有多大难度,因为经过多年的积累后,很多规则已经成型了。对于我们来说真正难的,是机器学习背后的算法所涉及的基础数学原理,包括向量、矩阵等等。
我们可以来看下机器学习的整个知识体系。单从数学角度来看,这个覆盖范围非常广,有向量积分、矩阵分解等等,但最最核心的还是线性代数。所以说,不要再问我为什么自己学不会机器学习、人工智能了,因为你没有学好线性代数。
不过,你可千万不要觉得,学了线性代数之后,实际应用就只有机器学习。如果这么想,那就太局限了。
线性代数是计算机很多领域的基础。比如,如何让3D图形显示到二维屏幕上?这是线性代数在图形图像学中的应用。如何提高密码被破译的难度?这个密码学问题,用线性代数中的有限向量空间可以很好地解决。
线性代数的应用真的非常广泛。掌握了线性代数这样的基础学科知识,我们其实就相当于有了数学这个利器,为其他领域的实际应用打下了非常好、非常扎实的基础。最简单、最直接的利益——你不仅可以在工作中进行算法调优,还能成为公司创新团队的主力。
到底该怎么学线性代数?
既然线性代数是机器学习最底层的知识,如果我们想要在机器学习上有所作为,学会线性代数是必须的。那该怎么学呢?
我估计你肯定看过外面很多书或者课程,我也看过。它们无一例外都是直接上来就给你讲机器学习的应用实践,然后里面穿插了一些数学知识,从实践的角度切入。这样编排课程当然没问题,优点是入门容易,但它的缺点也是显而易见的。这样学下来,很多时候,你只知道固定的应用场景,死记硬背几个知识点容易,但是数学知识并不牢固。当遇到实际问题的时候,你除了套公式之外,还是只能干瞪眼,根本没有真正吃透背后的原理。
因此,从我自己学习的经验出发,在技术领域里,我更推荐自下而上的学习方式,也就是从底层基础概念开始,一步步循序渐进往上走,一直走到应用实践。当然,这个方式也有缺点,那就是入门的时候困难,可能会遇到很多知识阻碍,很多人都会中途放弃。这些学习经历我都深有体会。
所以,我运用了自下而上的方式来进行讲解,同时,讲解每个知识点的时候,我都会加入一些和理论有关的实践讲解。这样就能够帮你由里及表,融会贯通,在搭建起知识体系的同时,可以获得螺旋式上升的学习效果。
为了让你能更加系统地学习线性代数,在设计“重学线性代数”这门课时,我还真是下了一番苦功夫。下面就给你详细介绍下这门课的两大模块。
第一个模块是基础篇,我们主要讲线性代数的理论基础。
我会从最简单、也是你最熟悉的线性方程组说起,在这基础上引出向量和矩阵,并通过矩阵来讲“解线性方程组”的不同方法(有直接法,也有实践中用得最多的间接迭代法)。然后,我会在向量和矩阵的基础上讲线性空间,因为在实践中,更多的是对集合的操作,也就是对线性空间的操作。线性空间好比是容器,它包含了向量以及向量的运算。基础篇的最后,我还会为你介绍解析几何,是解析几何使得向量从抽象走向了具象,让向量具有了几何的含义,比如:计算向量的长度、之间的距离和角度,这在机器学习的主成分分析PCA中是非常有用的。
第二个模块是应用篇,我会结合线性代数的基础理论,讲解线性代数在计算机科学中的应用。
有了之前的基础后,你再来看应用实践就会觉得简单很多。当其中会涉及一些线性代数以外的数学领域时,我也会给予一定的说明。
特别地,我要强调一下。在每一讲最后我都特意设计了“线性代数练习场”,带你通过练习来巩固学到的知识点。所以,这个小板块一定要重视起来,期待和你一起在实践中探索。
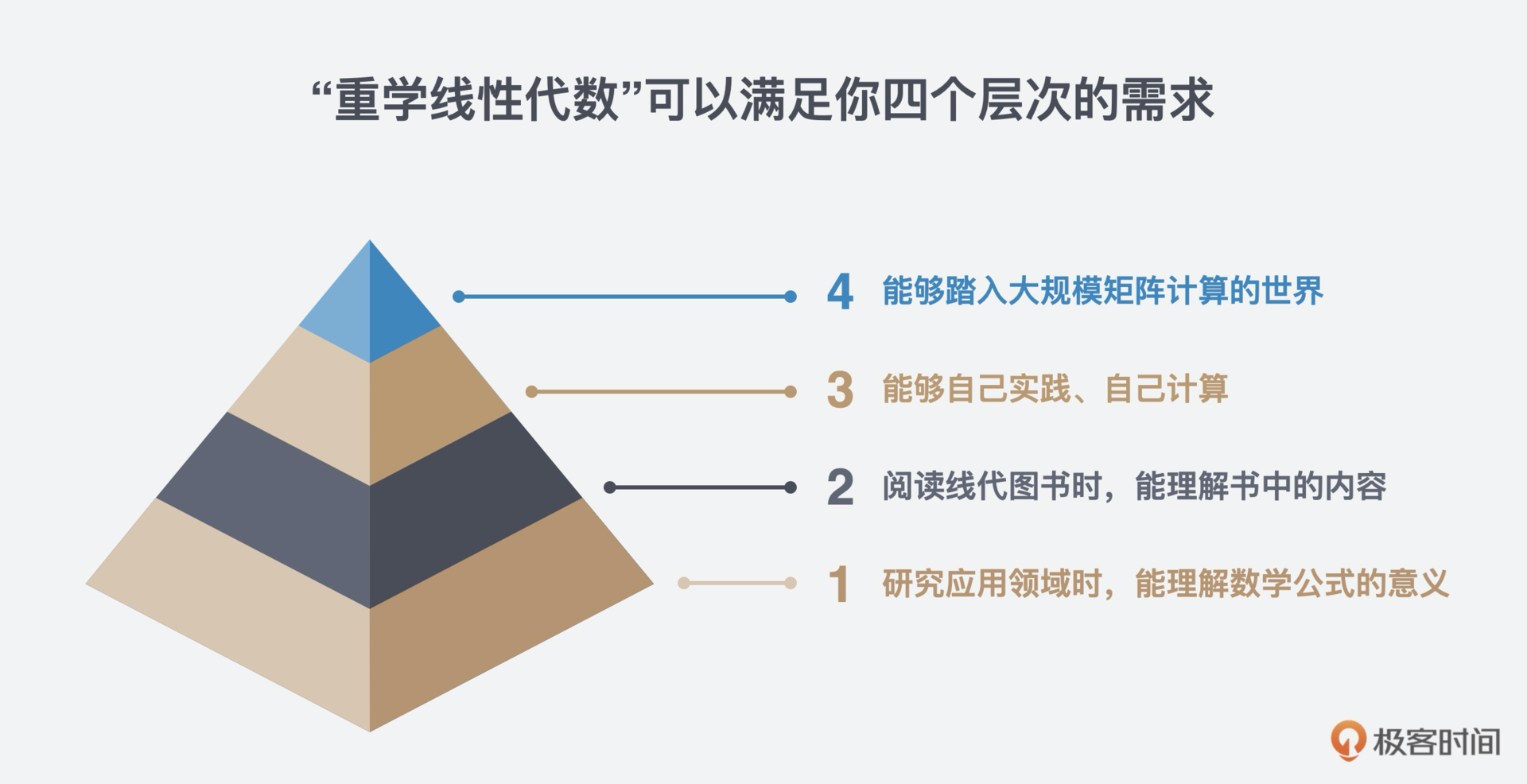
所以从整体来说,“重学线性代数”可以满足你四个层次的需求:
- 第一层次:在研究应用领域时,希望能够理解数学公式的意义。
- 第二层次:在阅读线性代数参考书时,希望理解书中的内容。
- 第三层次:能够自己实践、自己计算。
- 第四层次:能够踏入大规模矩阵计算的世界。
好了,到这里,我想说的已经差不多了,不知道你有没有准备好,跟我一起学习了呢?
进入DT时代后,很多企业都开始着手做数字化转型。站在从业者的角度,有了数字化的基础数据,我相信,终有一天人工智能将定义下一代软件解决方案,这是一个巨大的机会。
我希望在这个机会真正到来前,你能和我一起,一步步地、深入浅出地学习线性代数这门数学基础课,成为企业研究机构的创新力量之一。我也非常希望,通过这门课程的学习,你能对线性代数能有一个重新的认识,让线性代数融入到你的工作和生活中,真正改变你的工作和生活,让它成为你的翅膀。
当然,线性代数只是一个开始,在实际解决问题时,还需要用到很多其它的数学知识,我也会继续保持学习的心态,来和你一起探讨数学,一起更新最新的前沿知识,学习永无止境。
最后,让我们整装出发,一起来探索线性代数的世界,感受腾飞的乐趣吧!