96 lines
9.3 KiB
Markdown
96 lines
9.3 KiB
Markdown
# 45 | 线性代数篇答疑和总结:矩阵乘法的几何意义是什么?
|
||
|
||
你好,我是黄申。今天是线性代数的答疑和总结。
|
||
|
||
在这个模块中,我们讲了不少向量、矩阵、线性方程相关的内容。看到大家在留言区的问题,今天我重点说说矩阵乘法的几何意义,以及为什么SVD中$X’X$的特征向量组成了$V$矩阵,而$XX’$的特征向量组成了$U$矩阵。最后,我会对整个线性代数的模块做一个总结。
|
||
|
||
## 矩阵乘法的几何意义
|
||
|
||
首先,我们来说说矩阵乘法所代表的几何意义。
|
||
|
||
在阐述PCA主成分分析的时候,我们聊过为什么这个方法要研究协方差矩阵的特征值和特征向量。其中,我提到对某个向量左乘一个矩阵,实际上是对这个向量进行了一次变换。某个矩阵的特征向量表示了这个矩阵在空间中的变换方向,这些方向都是正交或者趋于正交的,而特征值表示每个方向上伸缩的比例。今天,我会继续深入这个话题,结合实例,给出更详细地解释。
|
||
|
||
多维的向量空间很难理解,所以我们还是从最简单的二维空间开始。首先,我们需要明白什么是二维空间中的正交向量。正交向量的定义非常简单,只要两个向量的点乘结果为0,那么它们就是正交的。在酉矩阵之中,矩阵和矩阵的转置相乘为单位矩阵,只有向量自己点乘自己值为1,而不同向量之间点乘值为0,所以不同的向量之间是正交的。
|
||
|
||
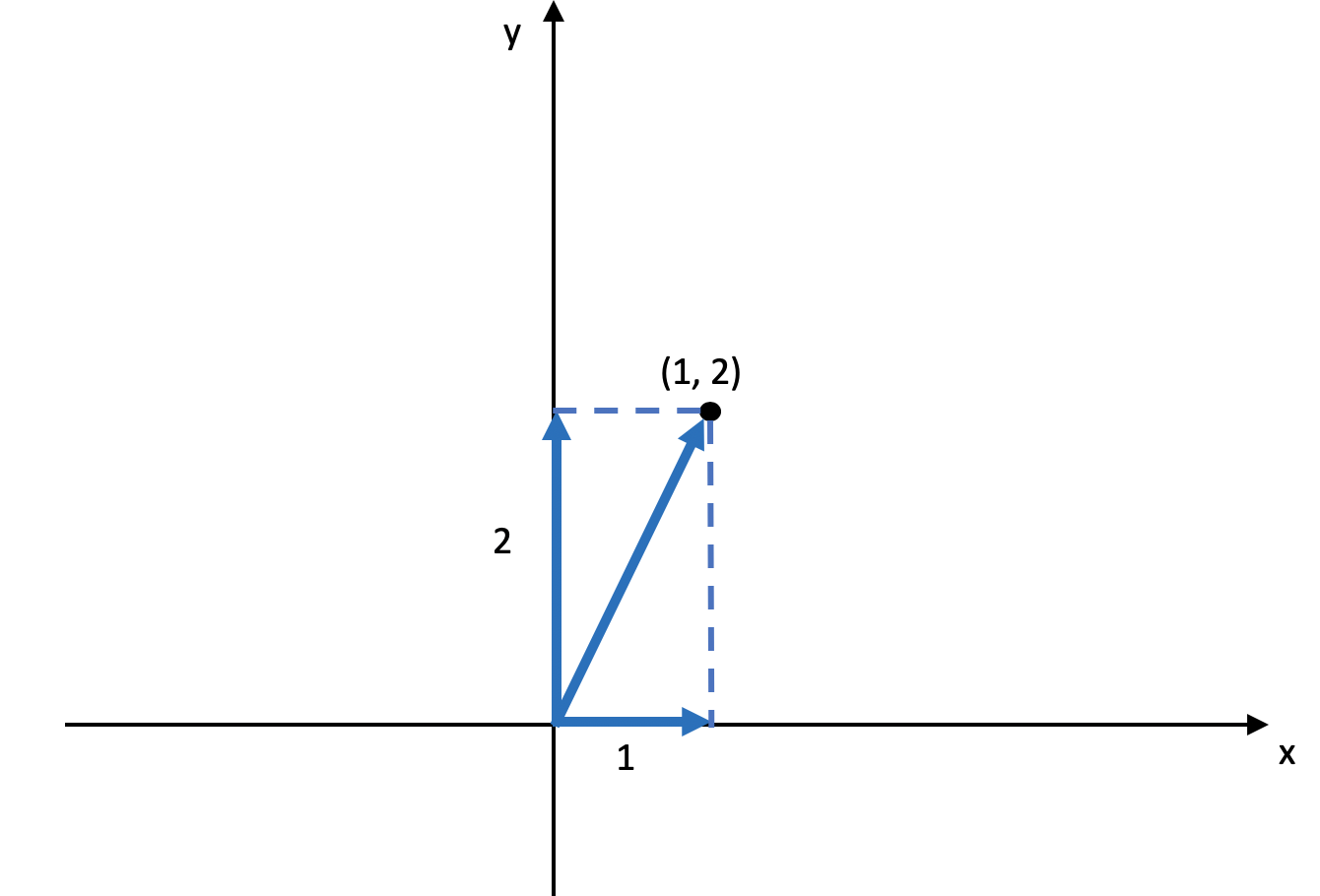
理解了正交向量之后,我们来定义一个二维空间,这个空间的横坐标为$x$,纵坐标为$y$,空间中的一个点坐标为$(1,2)$,对于这个点,我们可以把从原点到它的直线投影到$x$轴和$y$轴,这个直线在$x$轴上投影的长度为1,在y轴上投影的长度为2。我使用下图来表示。
|
||
|
||
|
||
|
||
对于这个点,我们使用一个矩阵$X\_1$左乘这个点的坐标,你可以看看会发生什么。
|
||
|
||
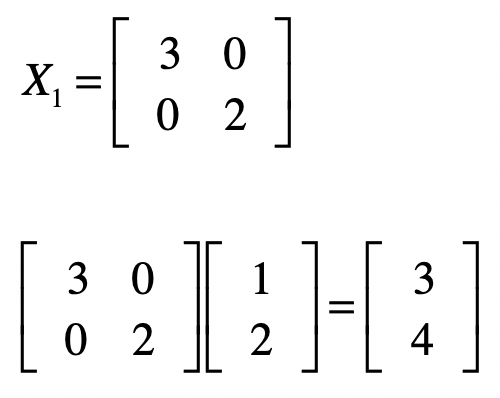
|
||
|
||
我们把结果转成坐标系里的点,它的坐标是$(3, 4)$,把从原点到$(1,2)$的直线,和从原点到$(3,4)$的直线进行比较,你会发现直线发生了旋转,而且长度也发生了变化,这就是矩阵左乘所对应的几何意义。我们还可以对这个矩阵$X\_1$分析一下,看看它到底表示了什么含义,以及为什么它会导致直线的旋转和长度发生变化。
|
||
|
||
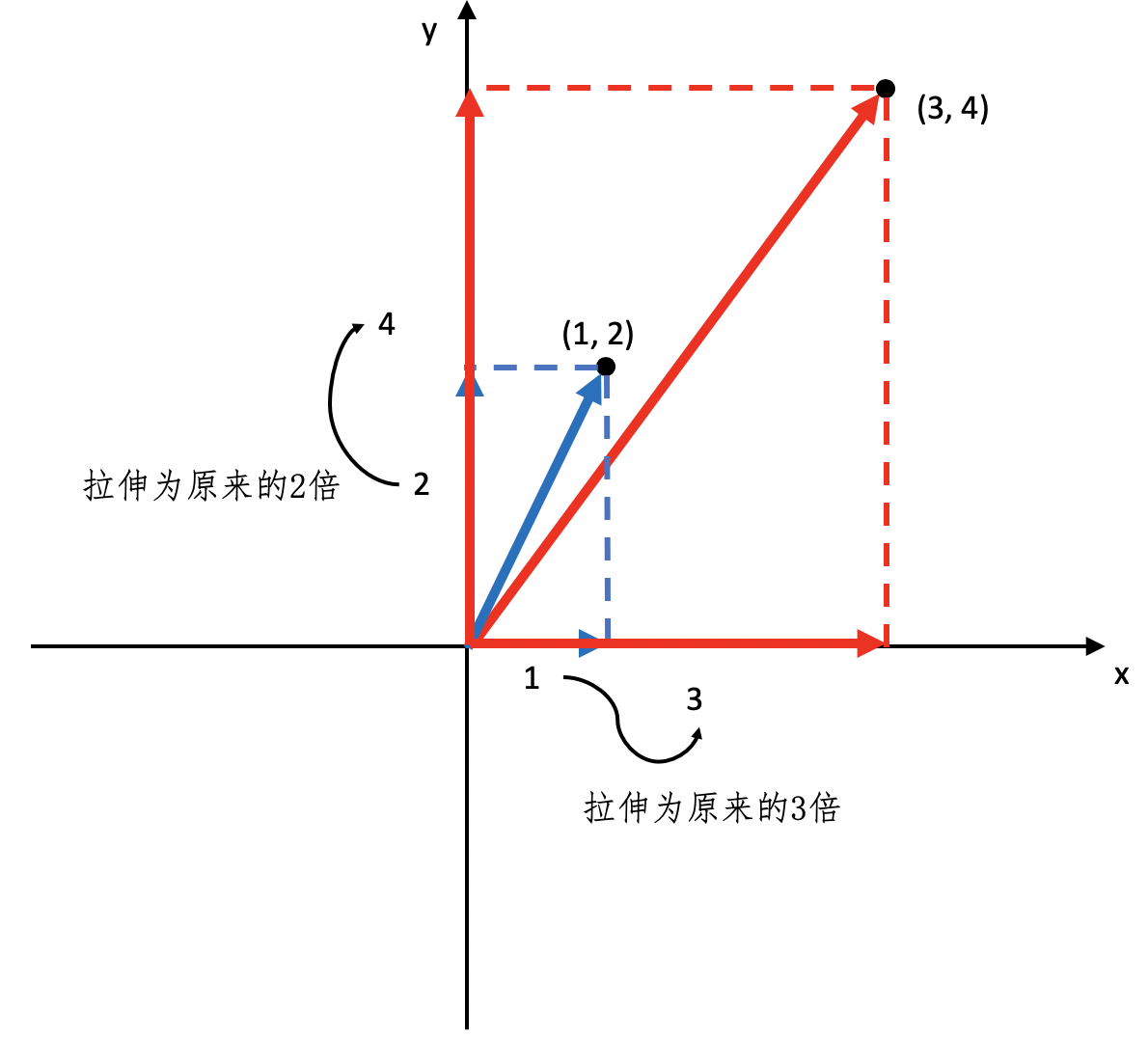
之前我讲过,要看一个矩阵的特征,需要分析它的特征向量和特征值。由于矩阵$X\_1$是一个对角矩阵,所以特征值很容易求解,分别是3和2。而对应的特征向量是$\[1, 0\]$和$\[0, 1\]$。在二维坐标中,坐标\[1, 0\]实际上表示的是$x$轴的方向,而\[0, 1\]实际上表示的是$y$轴的方向。特征值3对应特征向量\[1, 0\]就表明在$x$轴方向拉伸为原来的3倍,特征值2对应特征向量\[0, 1\]就表明在$y$轴方向拉伸2倍。所以,矩阵$X\_1$的左乘,就表示把原有向量在$x$轴上拉伸为原来的3倍,而在$y$轴上拉伸为原来的2倍。我用下面这张图来展示。
|
||
|
||
|
||
|
||
我们还可以从另一个角度来验证这点,把从原点到$(3, 4)$的直线进行分解,我们会发现这个直线在$x$轴上投影的长度为3,为原来的3倍,而在$y$轴上投影的长度为4,为原来的2倍。
|
||
|
||
当然,矩阵的特征向量不一定是$x$轴和$y$轴,它们可以是二维空间中任何相互正交的向量。下面,我们再来看一个稍微复杂一点的例子。这次我们从两个正交的向量开始。
|
||
|
||
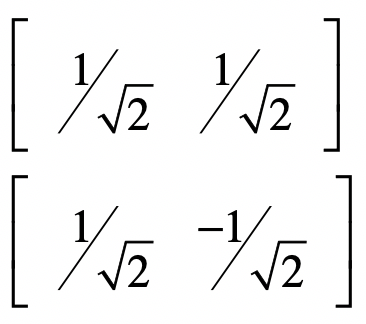
|
||
|
||
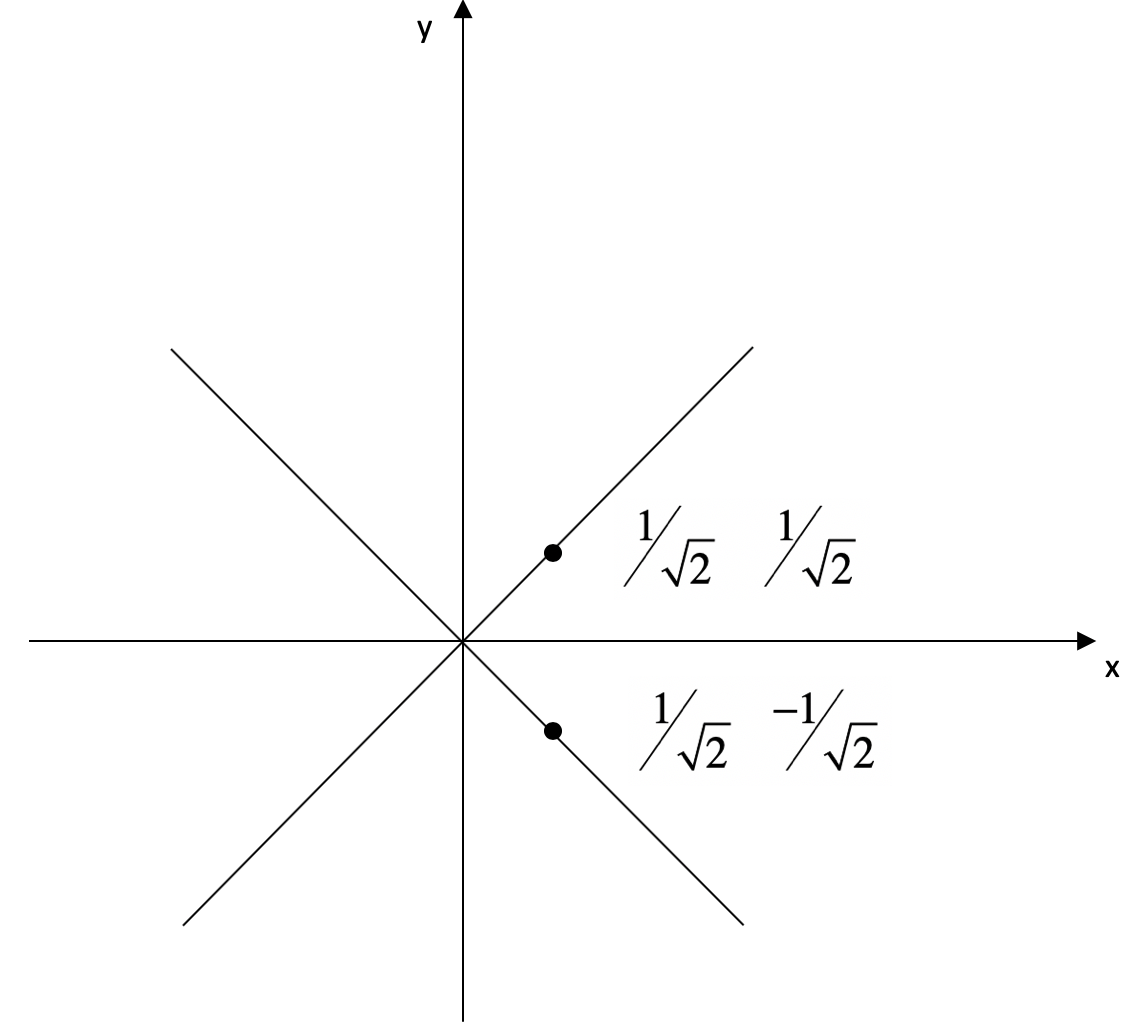
我使用下面这张图展示了这两个向量在空间的方向。
|
||
|
||
|
||
|
||
然后我用这两个向量构建一个矩阵$V$。
|
||
|
||
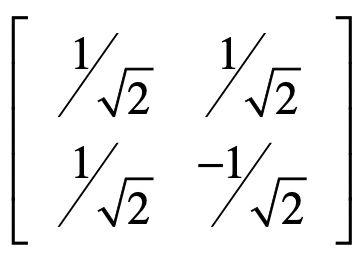
|
||
|
||
之所以使用这样一个例子,是因为$V$是一个酉矩阵,也就是说$VV’=I$,所以我们可以使用它,外加一个特征值组成的对角矩阵$Σ$,来构建另一个用于测试的矩阵$X\_2$。我在SVD的那一讲,介绍过对称方阵可以进行特征值分解,所以我们可以通过$V$和$Σ$,获得一个对称方阵$X\_2=VΣV’$。
|
||
|
||
我们假设两个特征值分别是0.5和2,所以有:
|
||
|
||
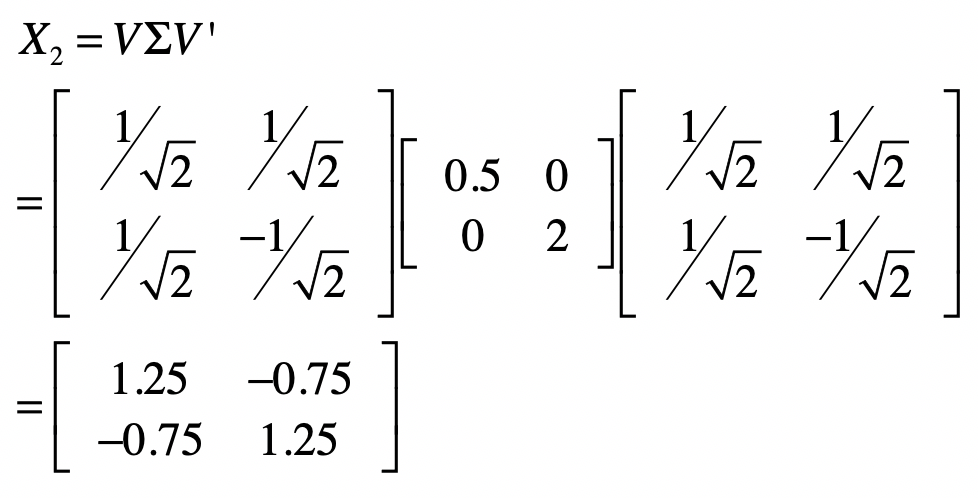
|
||
|
||
根据我们之间的解释,如果让这个矩阵$X\_2$左乘任何一个向量,就是让向量沿$\[\\frac{1}{\\sqrt{2}} \\frac{1}{\\sqrt{2}}\]$方向压缩一半,而在$\[\\frac{1}{\\sqrt{2}} \\frac{-1}{\\sqrt{2}}\]$方向增加两倍。为了验证这一点,我们让$X\_2$左乘向量$(1, 2)$,获得新向量:
|
||
|
||
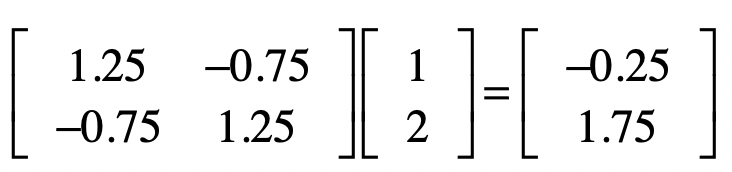
|
||
|
||
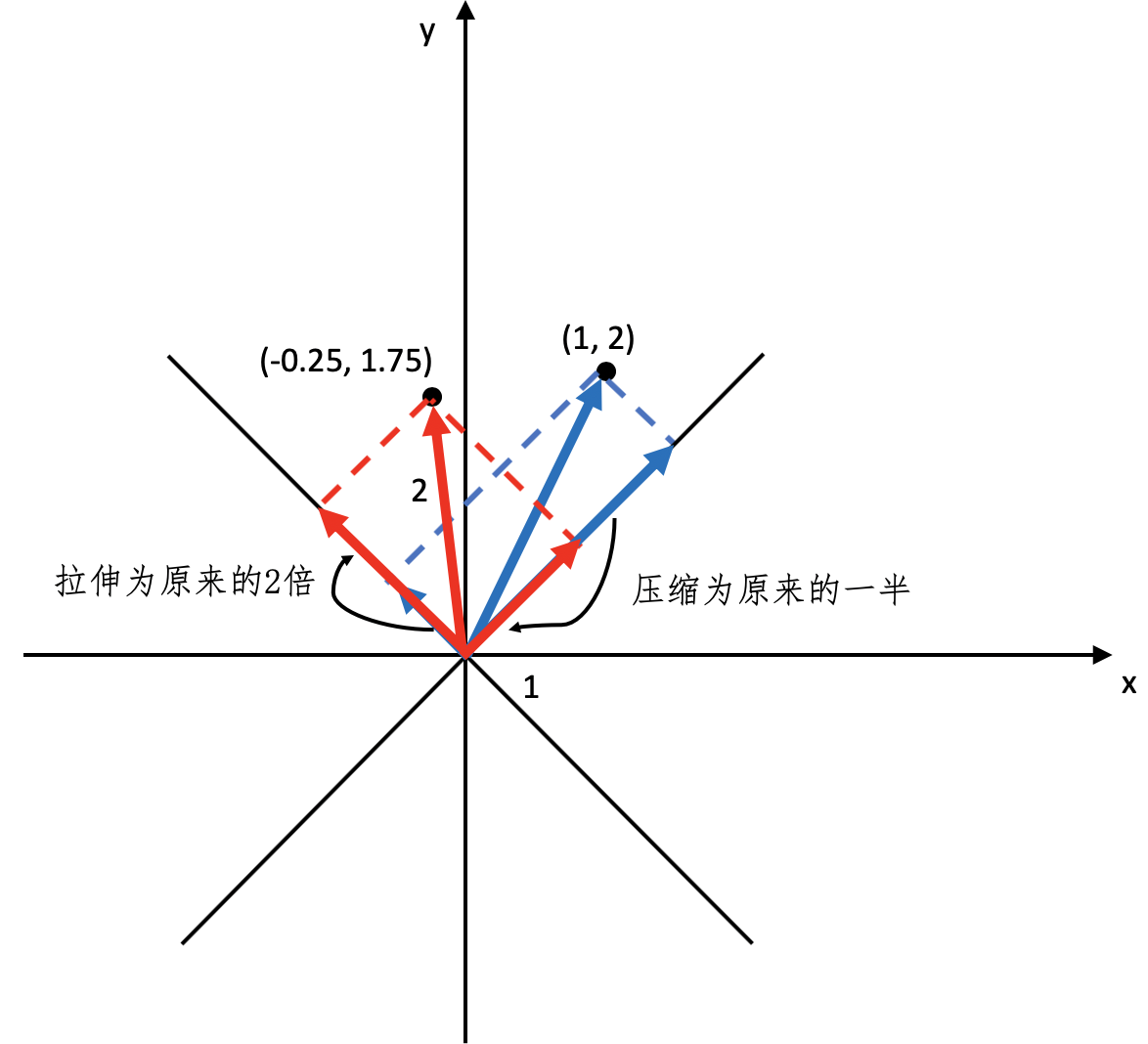
把这个新的坐标$(-0.25, 1.75)$和原坐标$(1,2)$都放到二维坐标系中,并让它们分别在$\[\\frac{1}{\\sqrt{2}} \\frac{1}{\\sqrt{2}}\]$和$\[\\frac{1}{\\sqrt{2}} \\frac{-1}{\\sqrt{2}}\]$这两个方向进行投影,然后比较一下投影的长度,你就会发现伸缩的变化了。我使用下面这张图来帮你理解。
|
||
|
||
|
||
|
||
弄清楚了矩阵左乘向量的几何意义,那么矩阵左乘矩阵的几何意义也就不难理解了。假设我们让矩阵$X$左乘矩阵$Y$,那么可以把右矩阵$Y$看作一堆列向量的集合,而左乘矩阵$X$就是对每个$Y$中的列向量进行变换。另外,如果二维空间理解了,那么三维、四维直到$n$维空间就可以以此类推了。
|
||
|
||
## SVD分解中的$U$和$V$矩阵
|
||
|
||
在讲解SVD奇异值分解的时候,我们解释了$X’X$的特征向量组成了SVD中的$V$矩阵,而$XX’$的特征向量组成了SVD中的$U$矩阵。不过,我们还没有证明这两点。今天我来说说如何证明它们。首先,我们来看看$V$矩阵的证明。
|
||
|
||
$X=UΣV’$
|
||
$X’=VΣ’U’$
|
||
$X’X=(VΣ’U)(UΣV’)=VΣ’(U’U)Σ’V’=VΣ^2V’)$
|
||
|
||
其中,$(UΣV’)‘=VΣ’U’$的证明,我们在最小二乘法的讲解过程中证明过。另外,$U$是酉矩阵,所以$U’U=I$。$Σ$是对角矩阵,所以$Σ’Σ=Σ2$,而且$Σ2$仍然是对角矩阵。
|
||
|
||
由于$Σ2$是对角矩阵,所以通过$X’X=VΣ2V’$,我们可以看出$V$中的向量就是$X’X$的特征向量,而特征值是$Σ2$对角线上的值。
|
||
|
||
同理,我们也可以证明$U$中的向量就是$XX’$的特征向量。
|
||
|
||
$X=UΣV’$
|
||
$X’=VΣ’U’$
|
||
$XX’=(UΣV’)(VΣ’U’)=UΣ(V’V)Σ’U’=UΣ^2U’)$
|
||
|
||
从这个证明的过程,我们也发现了,XX’或者X’X特征值矩阵等于奇异值矩阵的平方,也就是说我们可以通过求出X’X特征值的平方根来求奇异值。
|
||
|
||
## 总结
|
||
|
||
回答完两个问题之后,我来总结一下线性代数这个模块。
|
||
|
||
线性代数最基本的概念包括了向量、矩阵以及对应的操作。向量表示了一组数的概念,非常适合表示一个对象的多维特征,因此被广泛的运用在信息检索和机器学习的领域中。而矩阵又包含了多个向量,所以适合表示多个数据对象的集合。同时,矩阵也可以用于表达二维关系,例如网页的邻接矩阵,用户对物品的喜好程度,关键词在文档中的tf-idf等等。
|
||
|
||
由于向量和矩阵的特性,我们可以把它们运用在很多算法和模型之中。向量空间模型定义了向量之间的距离或者余弦夹角,我们可以利用这些指标来衡量数据对象之间的相似程度,并把这种相似程度用于定义查询和文档之间的相关性,或者是文档聚类时的归属关系。矩阵的运算体现了对多个向量同时进行的操作,比如最常见的左乘,就可以用在计算PageRank值,协同过滤中的用户或者物品相似度等等。
|
||
|
||
当然,矩阵的运用还不只计算数据对象之间的关系。最小二乘法的实现、PCA主成分的分析、SVD奇异值的分解也可以基于矩阵的运算。这些都可以帮助我们发现不同维度特征之间的关系,并利用这些关系找到哪些特征更为重要,选择或者创建更为重要的特征。
|
||
|
||
有的时候,线性代数涉及的公式和推导比较繁琐。在思考的过程中,我们可以把矩阵的操作简化为向量之间的操作,而把向量之间的操作简化为多个变量之间的运算。另外,我们可以多结合实际的案例,结合几何空间、动手推算,甚至可以编程实现某些关键的模块,这些都有利于理解和记忆。
|
||
|
||
## 思考题
|
||
|
||
我想听你说说,学习完了编程领域中常用的线性代数知识,你有哪些收获和心得?
|
||
|
||
欢迎留言和我分享,也欢迎你在留言区写下今天的学习笔记。你可以点击“请朋友读”,把今天的内容分享给你的好友,和他一起精进。
|
||
|