190 lines
9.7 KiB
Markdown
190 lines
9.7 KiB
Markdown
# 数学专栏课外加餐(二) | 位操作的三个应用实例
|
||
|
||
你好,我是黄申。欢迎来到第二次课外加餐时间。
|
||
|
||
## 位操作的应用实例
|
||
|
||
留言里很多同学对位操作比较感兴趣,我这里通过计算机中的位操作的几个应用,来帮你理解位操作。
|
||
|
||
### 1.验证奇偶数
|
||
|
||
在[第2节](https://time.geekbang.org/column/article/72163)里,我提到了,奇偶数其实也是余数的应用。编程中,我们也可以用位运算来判断奇偶数。
|
||
|
||
仔细观察,你会发现偶数的二进制最后一位总是0,而奇数的二进制最后一位总是1,因此对于给定的某个数字,我们可以把它的二进制和数字1的二进制进行按位“与”的操作,取得这个数字的二进制最后一位,然后再进行判断。
|
||
|
||
我这里写了一段代码,比较了使用位运算和模运算的效率,我统计了进行1亿次奇偶数判断,使用这两种方法各花了多少毫秒。如果在你的机器上两者花费的时间差不多,你可以尝试增加统计的次数。在我的机器上测试下来,同样次数的奇偶判断,使用位运算的方法耗时明显更低。
|
||
|
||
```
|
||
public class Lesson1_append1 {
|
||
|
||
public static void main(String[] args) {
|
||
|
||
int even_cnt = 0, odd_cnt = 0;
|
||
long start = 0, end = 0;
|
||
|
||
start = System.currentTimeMillis();
|
||
for (int i = 0; i < 100000000; i++) {
|
||
|
||
if((i & 1) == 0){
|
||
even_cnt ++;
|
||
}else{
|
||
odd_cnt ++;
|
||
}
|
||
|
||
}
|
||
end = System.currentTimeMillis();
|
||
System.out.println(end - start);
|
||
System.out.println(even_cnt + " " + odd_cnt);
|
||
|
||
even_cnt = 0;
|
||
odd_cnt = 0;
|
||
start = 0;
|
||
end = 0;
|
||
|
||
start = System.currentTimeMillis();
|
||
for (int i = 0; i < 100000000; i++) {
|
||
|
||
if((i % 2) == 0){
|
||
even_cnt ++;
|
||
}else{
|
||
odd_cnt ++;
|
||
}
|
||
|
||
}
|
||
end = System.currentTimeMillis();
|
||
System.out.println(end - start);
|
||
System.out.println(even_cnt + " " + odd_cnt);
|
||
|
||
}
|
||
}
|
||
|
||
```
|
||
|
||
### 2.交换两个数字
|
||
|
||
你应该知道,要想在计算机中交换两个变量的值,通常都需要一个中间变量,来临时存放被交换的值。不过,利用异或的特性,我们就可以避免这个中间变量。具体的代码如下:
|
||
|
||
```
|
||
x = (x ^ y);
|
||
y = x ^ y;
|
||
x = x ^ y;
|
||
|
||
```
|
||
|
||
把第一步代入第二步中,可以得到:
|
||
|
||
```
|
||
y = (x ^ y) ^ y = x ^ (y ^ y) = x ^ 0 = x
|
||
|
||
```
|
||
|
||
把第一步和第二步的结果代入第三步中,可以得到:
|
||
|
||
```
|
||
x = (x ^ y) ^ x = (x ^ x) ^ y = 0 ^ y = y
|
||
|
||
```
|
||
|
||
这里用到异或的两个特性,第一个是两个相等的数的异或为0,比如x^x= 0;第二个是任何一个数和0异或之后,还是这个数不变,比如0^y=y。
|
||
|
||
### 3.集合操作
|
||
|
||
集合和逻辑的概念是紧密相连的,因此集合的操作也可以通过位的逻辑操作来实现。
|
||
|
||
假设我们有两个集合{1, 3, 8}和{4, 8}。我们先把这两个集合转为两个8位的二进制数,从右往左以1到8依次来编号。
|
||
|
||
如果某个数字在集合中,相应的位置1,否则置0。那么第一个集合就可以转换为10000101,第二个集合可以转换为10001000。那么这两个二进制数的按位与就是10000000,只有第8位是1,代表了两个集合的交为{8}。而这两个二进制数的按位或就是10001101,第8位、第4位、第3位和第1位是1,代表了两个集合的并为{1, 3, 4, 8}。
|
||
|
||
说到这里,不禁让我想起Elasticsearch的BitSet。我曾经使用Elasticsearch这个开源的搜索引擎来实现电商平台的搜索。
|
||
|
||
当时为了提升查询的效率,我使用了Elasticsearch的Filter查询。我研究了一下这个Filter查询的原理,发现它并没有考虑各种文档的相关性得分,因此它可以把文档匹配关键字的情况,转换成了一个BitSet。
|
||
|
||
你可以把BitSet想成一个巨大的位数组。每一位对应了某篇文档是否和给定的关键词匹配,如果匹配,这一位就置1,否则就置0。每个关键词都可以拥有一个BitSet,用于表示哪些文档和这个关键词匹配。那么要查看同时命中多个关键词的文档有哪些,就是对多个BitSet求交集。利用上面介绍的按位与,这点是很容易实现的,而且效率相当之高。
|
||
|
||
## 二分查找时的两个细节
|
||
|
||
[第3节](https://time.geekbang.org/column/article/72243)我介绍了迭代法,并讲解了相关的代码实现。其中,有两个细节我在这里补充说明一下。
|
||
|
||
第一个是关于**中间值的计算**。我优化了两处代码,分别是Lesson3\_2的第16行和Lesson3\_3的第22行。
|
||
|
||
其中,Lesson3\_2的第16行由原来的:
|
||
|
||
```
|
||
double middle = (min + max) / 2;
|
||
|
||
```
|
||
|
||
改为:
|
||
|
||
```
|
||
double middle = min + (max - min) / 2;
|
||
|
||
```
|
||
|
||
Lesson3\_3的第22行由原来的:
|
||
|
||
```
|
||
int middle = (left + right) / 2;
|
||
|
||
```
|
||
|
||
改为:
|
||
|
||
```
|
||
int middle = left + (right - left) / 2;
|
||
|
||
```
|
||
|
||
这两处改动的初衷都是一样的,是为了避免溢出。在第一篇加餐中,介绍负数的加法时,我已经解释了什么是溢出。那这里为什么会发生溢出呢?我以第二处代码为例来讲解下。
|
||
|
||
从理论上来说,(left+right)/2=left+(right-left)/2。可是,我们之前说过,计算机系统有自身的局限性,无论是何种数据类型,都有一个上限或者下限。一旦某个数字超过了这些限定,就会发生溢出。
|
||
|
||
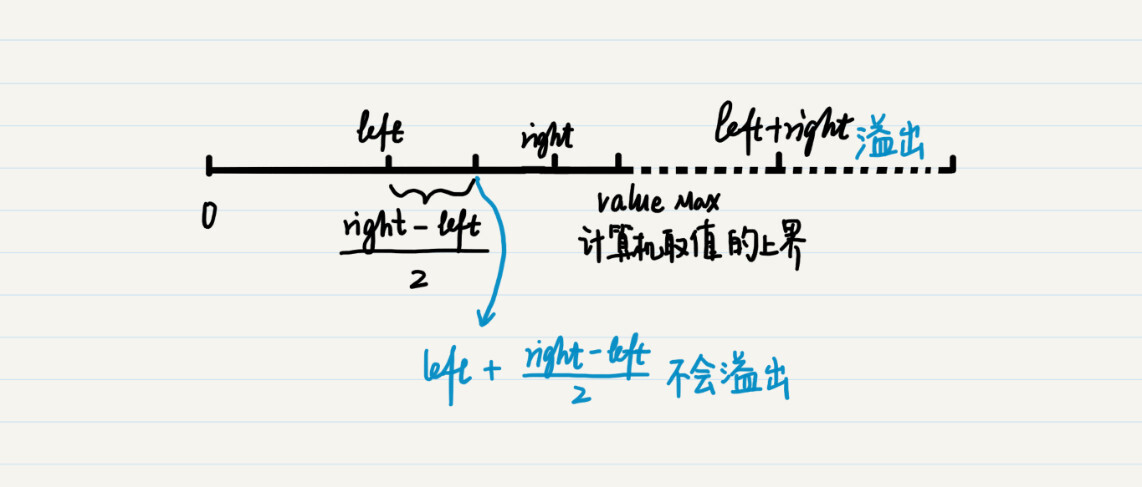
对于变量left和right而言,在定义的时候都指定了数据类型,因此不会超出范围。可是,left+right的和就不一定了。从下图可以看出,当left和right都已经很接近某个数据类型的最大值时,两者的和就会超过这个最大值,发生上溢出。这也是为什么最好不用通过(left+right)/2来求两者的中间值。
|
||
|
||
|
||
|
||
那么为什么left + (right -left)/2就不会溢出呢?首先,right是没有超过最大值的,那么(right -left)/2自然也就没有超过范围,即使left加上了(right -left)/2,也不会超过right的值,所以运算的整个过程都不会产生溢出。
|
||
|
||
第二个是关于误差百分比和绝对误差。在Lesson3\_2中有这么一行:
|
||
|
||
```
|
||
double delta = Math.abs((square / n) - 1);
|
||
|
||
|
||
```
|
||
|
||
这里我使用了误差的百分比,也就是误差值占输入值n的比例。其实绝对误差也是可以的,不过我在这里考虑了n的大小。比如,如果n是一个很小的正整数,比如个位数,那么误差可能要精确到0.00001。但是如果n是一个很大的数呢?比如几个亿,那么精确到0.00001可能没有多大必要,也许精确到0.1也就可以了。所以,使用误差的百分比可以避免由于不同的n,导致的迭代次数有过大差异。
|
||
|
||
由于这里n是大于1的正整数,所以可以直接拿平方值square去除以n。否则,我们要单独判断n为0的情况,并使用绝对误差。
|
||
|
||
## 关于迭代法、数学归纳法和递归
|
||
|
||
从第3节到第6节,我连续介绍了迭代法、数学归纳法、递归。这些概念之间存在相互联系,又不完全一样,很多同学对此也有一些疑惑。所以,这里我来帮你梳理一下。
|
||
|
||
迭代法和递归都是通过不断反复的步骤,计算数值或进行操作的方法。迭代一般适合正向思维,而递归一般适合逆向思维。而递归回溯的时候,也体现了正向递推的思维。它们本身都是抽象的流程,可以有不同的编程实现。
|
||
|
||
对于某些重复性的计算,数学归纳法可以从理论上证明某个结论是否成立。如果成立,它可以大大节约迭代法中数值计算部分的时间。不过,在使用数学归纳法之前,我们需要通过一些数学知识,假设命题,并证明该命题成立。
|
||
|
||
对于那些无法使用数学归纳法来证明的迭代问题,我们可以通过编程实现。这里需要注意的是,广义上来说,递归也是迭代法的一种。不过,在计算机编程中,我们所提到的迭代是一种具体的编程实现,是指使用循环来实现的正向递推,而递归是指使用函数的嵌套调用来实现的逆向递推。当然,两种实现通常是可以相互转换的。
|
||
|
||
循环的实现很容易理解,对硬件资源的开销比较小。不过,循环更适合“单线剧情”,例如计算2^n,n!,1+2+3+…+n等等。而对于存在很多“分支剧情”的复杂案例而言,使用递归调用更加合适。
|
||
|
||
利用函数的嵌套调用,递归编程可以存储很多中间变量。我们可以很轻松地跟踪不同的分支,而所有这些对程序员基本是透明的。如果这时使用循环,我们不得不自己创建并保存很多中间变量。当然,正是由于这个特性,递归比较消耗硬件资源。
|
||
|
||
递归编程本身就体现了分治的思想,这个思想还可以延伸到集群的分布式架构中。最近几年比较主流的MapReduce框架也体现了这种思想。
|
||
|
||
综合上面说的几点,你可以大致遵循这样的原则:
|
||
|
||
* 如果一个问题可以被迭代法解决,而且是有关数值计算的,那你就看看是否可以假设命题,并优先考虑使用数学归纳法来证明;
|
||
|
||
* 如果需要借助计算机,那么优先考虑是否可以使用循环来实现。如果问题本身过于复杂,再考虑函数的嵌套调用,是否可以通过递归将问题逐级简化;
|
||
|
||
* 如果数据量过大,可以考虑采用分治思想的分布式系统来处理。
|
||
|
||
|
||
最后,给你留一道思考题吧。
|
||
|
||
在1到n的数字中,有且只有唯一的一个数字m重复出现了,其它的数字都只出现一次。请把这个数字找出来。提示:可以充分利用异或的两个特性。
|
||
|
||
好了,前面6讲的补充内容就到这里了。欢迎你留言给我。你也可以点击“请朋友读”,把今天的内容分享给你的好友,和他一起精进。
|
||
|