95 lines
13 KiB
Markdown
95 lines
13 KiB
Markdown
# 27|一致性与共识(二):它们是鸡生蛋还是蛋生鸡?
|
||
|
||
你好,我是陈现麟。
|
||
|
||
通过上节课的学习,我们了解了一致性模型的发展历史,同时还掌握了各个一致性模型之间的强弱差异,这样在极客时间后端技术的选型和演进过程中,你就能够做出最适合业务场景的选择了,这对于我们搭建分布式系统是非常关键的一个权衡。
|
||
|
||
其实一致性和共识是两个如影随形的概念,我们在讨论一致性的时候,总是会提到共识,同时我们在研究共识的时候,一致性也是不能绕过的话题。那么,你一定会很好奇它们之间的关系是什么?一致性和共识是像鸡生蛋和蛋生鸡这种非常紧密的关系呢?还是其他的比较弱的关系呢?
|
||
|
||
在这节课中,我们主要来讨论一致性与共识之间的关系,一方面解开你的疑问,另一方面通过探讨它们之间的关系,让你能够进一步理解一致性和共识。我们先一起来了解共识问题的场景与定义,然后分析达成共识所面临的挑战,最后再来探讨一致性和共识的关系。
|
||
|
||
## 共识问题的定义
|
||
|
||
在分布式系统中,共识(Consensus)问题是最重要,也是最基本的问题之一,**简单来说它就是多个节点(进程)对某一个事情达成一致的结果**。在分布式系统中,我们经常碰到这样的场景,比如在主从复制的模型中,需要在多个节点选举出 Leader 节点。由于有且只能有一个 Leader 节点,所以多个节点必须就哪一个节点是 Leader 这个决定达成一致。那么共识算法经常用于像选举 Leader 、分布式锁服务这样,有且只有一个能胜出的场景。
|
||
|
||
在讨论共识问题的时候,我们通常会做这样的形式化定义:一个或多个节点可以提议(Propose)某些值,而共识算法决定(Decide)采用其中某一个节点提议的某个值。比如在 Leader 选举的例子中,每一个节点都可以提议自己为 Leader 节点,而共识算法会让所有的节点对某一个节点为 Leader 达成一致。
|
||
|
||
所以,通过上面的讨论,我们可以得出共识算法必须满足的四个条件,具体如下。
|
||
|
||
* **一致同意(Uniform Agreement)**:所有协议的节点必须接受相同的决议。
|
||
* **诚实性(Integrity)**:所有节点不能反悔,即对一项提议,一个节点不能做两次决定。
|
||
* **合法性(Validity)**:如果决定了值 v ,则 v 一定是由某个节点所提议的。
|
||
* **可终止性(Termination)**:如果节点不崩溃,则一定可以达成决议。
|
||
|
||
其中,一致同意和诚实性定义了共识的核心思想:所有人都决定了相同的结果,并且一旦决定了,就不能再改变。
|
||
|
||
合法性主要是为了排除没有意义的解决方案。例如无论节点提议了什么值,都可以让所有节点始终以某一个固定值(如nil)达成共识的算法,这个算法满足一致同意和诚实性,但是由于达成共识的值是固定的,不是由某一个节点提出的,所以不满足合法性。
|
||
|
||
可终止性确保了,共识算法在部分节点故障的情况下,其他的节点也能达成一致,可终止性让共识算法能够容错。如果共识算法不需要容错是很容易实现的,比如将某一个节点指定为共识算法的“独裁者”,其他的节点必须同意该节点做出的所有决定。不过这个算法的问题是如果“独裁者”节点出现故障,系统就将无法达成共识了。
|
||
|
||
其实 2PC 协议就是不满足可终止性的共识协议。在 2PC 中,协调者节点就是“独裁者”节点,它在第一阶段通过收集参与者节点 Prepare 的响应做出决定,但是当协调者故障时,参与者就无法决定提交还是中止了。
|
||
|
||
到这里,你是否觉得共识问题非常简单呢?其实不然,共识问题是一个非常难的问题,如果处理不好共识,很有可能会出现各种问题或故障,比如在分布式锁服务 Leader 选举的场景中,如果出现两个 Leader,那么整个分布式锁服务就进入了脑裂的状态,锁的互斥性将会被破坏,使业务上出现不可预期的情况。
|
||
|
||
## 达成共识的挑战
|
||
|
||
我们已经知道共识处理不好,可能会出现各种问题或故障,那么接下来,我们就从共识理论出发,分析达成共识面临的挑战,提前发现问题,解决问题。
|
||
|
||
**第一个挑战是,在异步网络模型中,如果一个节点出现崩溃,那么共识就将无法达成,这就是大名鼎鼎的 “ FLP 不可能”**。但是在分布式系统中,节点的故障是我们必须要面对的问题,如果以 Leader 选举的场景来讨论,需要达成共识的一个主要场景就是, Leader 节点崩溃了,需要重新选择一个新的 Leader ,选择新的 Leader 需要达成共识,但是因为 “ FLP 不可能”,所以共识不能在节点崩溃的时候达成。
|
||
|
||
这样看来问题就无解了,但是在实际应用中,我们是可以通过 Raft 或者 Paxos 之类的共识算法来解决这一类问题的,这是否和 “FLP 不可能” 冲突了呢?
|
||
|
||
其实出现这个问题的根本原因是,在异步网络模型的定义中,网络中消息的传递延迟和节点的处理延迟是无上限的,所以对于消息是不能使用任何时钟或超时的,这样就导致在节点出现崩溃的时候,我们无法判断是否有节点崩溃,只能无限等待下去,使共识算法不能满足“可终止性”;**但是在真实的环境中,我们可以允许共识算法使用超时或其他方法,来识别可疑的崩溃节点(即使有时怀疑是错误的)**,这样就避免了无限等待,使达成共识成为一个可行的事情。
|
||
|
||
**第二个挑战与我们对分布式系统的故障模型定义有关。一般来说,在分布式系统中,我们对故障模型的定义是“崩溃-恢复失败”(Crash-Recovery Failure)模型**。简单来说就是,在一个节点很长时间没有返回消息时,我们不能确定它是因为崩溃,还是因为网络或者计算速度过慢等原因导致的。其中网络或者计算速度过慢等原因,都是可以恢复的,这个模型和我们现在的分布式模型是最匹配的。
|
||
|
||
而像 Raft 和 Paxos 之类的共识算法,我们可以在“崩溃-恢复失败”(Crash-Recovery Failure)模型上,通过超时来识别可疑的崩溃节点,这就解决了一个问题:一个或多个节点可以提议(Propose)某些值,而共识算法决定(Decide)采用其中某一个节点提议的某个值。
|
||
|
||
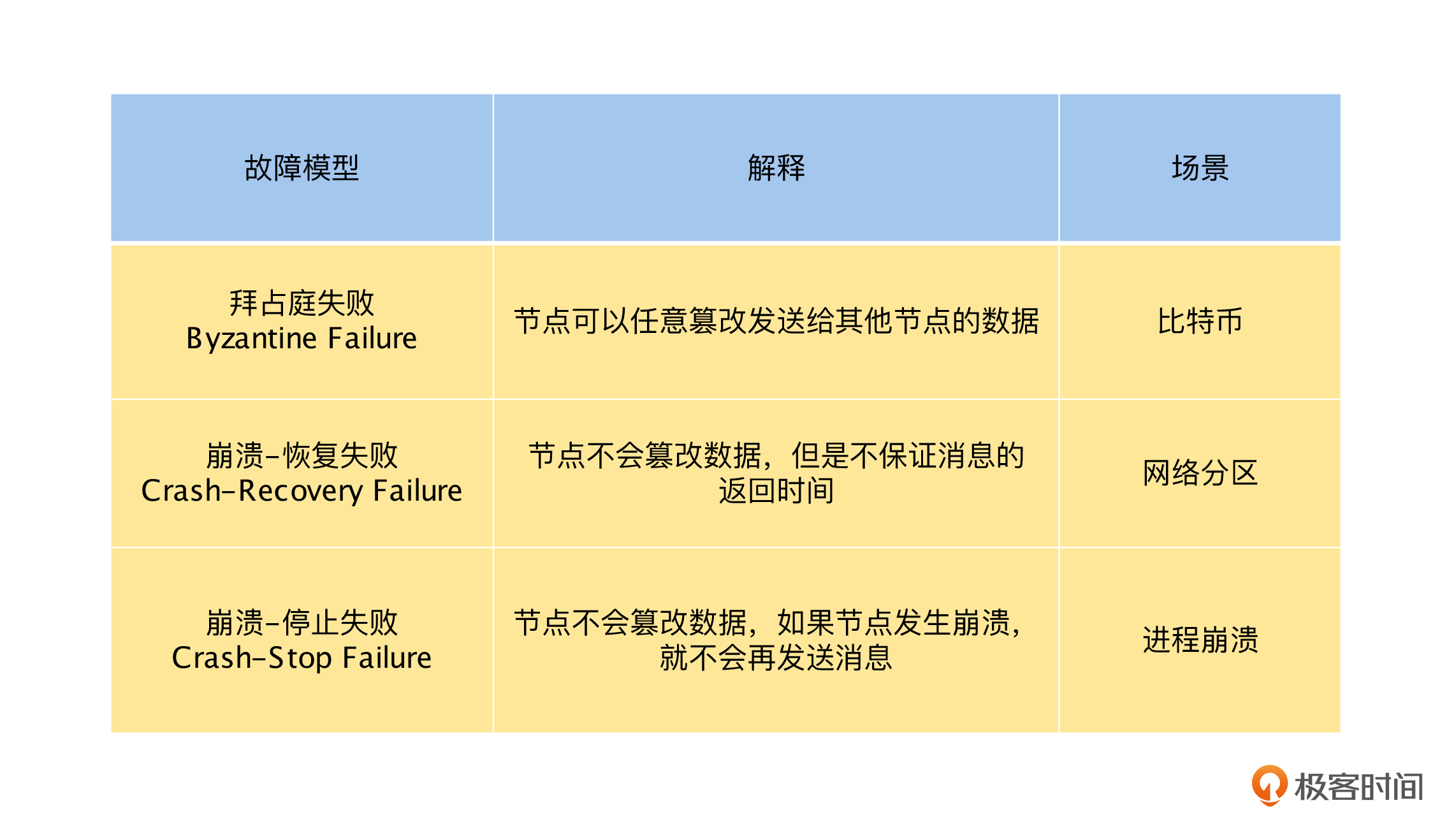
除此之外,还有“拜占庭失败”(Byzantine Failure)和“崩溃-停止失败”(Crash-Stop Failure)等模型。其中,“拜占庭失败”(Byzantine Failure)模型在“崩溃-恢复失败”(Crash-Recovery Failure)模型上,增加了节点会主动伪造和发布虚假消息的情况,由于这个情况在内网的分布式环境中几乎不会出现,并且要解决它的代价非常高,所以一般的共识算法,不会考虑解决“拜占庭失败”(Byzantine Failure) 模型下的共识问题。
|
||
|
||
但是,在公网的分布式环境中,是需要解决这个问题的,例如比特币是通过“工作量证明”这样的算法,利用经济学原理,让节点造假的成本高于收益,来避免节点发布虚假消息的。
|
||
|
||
而“崩溃-停止失败” (Crash-Stop Failure)模型在“崩溃-恢复失败”(Crash-Recovery Failure)模型上,去掉了节点崩溃后的不确定性,如果一个节点很长时间没有返回消息,那么它就是崩溃了,不会再回复什么消息,即崩溃后就立即停止。
|
||
|
||
但是,在实际的分布式场景中,由于网络或者计算太慢而故障的节点,待恢复后,很久之前响应的消息是会正常出现的。所以,如果共识算法只能处理“崩溃-停止失败”(Crash-Stop Failure)模型,就不能适应我们实际的网络环境了。接下来,我们总结一下课程中提到的三种故障模型,如下表所示。
|
||
|
||
|
||
|
||
最后,还要特别强调一点,我们应该尽量选择像 ZooKeeper 和 etcd 这样,开源并且经过了广泛应用而被验证的程序,来为我们的应用提供共识能力,而不是自己再依据 Raft 或 Paxos 算法实现一个共识算法。因为相对于实现一个共识算法,证明共识算法实现的正确性是一个更难的问题。
|
||
|
||
## 一致性和共识的关系
|
||
|
||
通过学习共识问题的定义和挑战,我们对共识问题有了一定的了解,接下来,我们将一致性和共识结合,讨论一下它们之间的关系,这里的一致性我们定义为一致性最强的线性一致性。
|
||
|
||
在本专栏[第 19 讲“主从复制”](https://time.geekbang.org/column/article/495283)的课程中,我们讨论过主从复制:主节点承接所有的写入操作,然后以相同的顺序将它们应用到从节点,从而使主、从副本节点的数据保持最终一致性。
|
||
|
||
如果在主节点或同步副本的从节点上读取数据,那么就是线性一致性的。当然如果数据库的读为快照读,由于不能读到最新版本的数据,这个情况下就不是线性一致性的。
|
||
|
||
到这里,你是否觉得线性一致性非常容易实现,而且和共识算法也没有什么关系呢?其实不然,在主从复制的模型中,如果主节点不出现故障,那么一切都非常美好,但是如果主节点发生崩溃了,应该怎么办呢?
|
||
|
||
首先,最简单的办法是**等待主节点修复**,如果主节点无法快速修复或者无法修复,那么系统的高可用就名存实亡了。对于等待主节点恢复的方式,我们可以理解为系统对之前达成主节点的共识是不可改变的。
|
||
|
||
其次,**人工切换主节点**,这个方案是可行的,不过它的时间不确定,或长或短。如果出故障的时候,找不到合适的人来操作,就会严重影响系统的可用性。对于这个方式,我们可以理解为,系统对于主节点的共识是由操作人员来提供的,这是一个来自“上帝”视角的共识。
|
||
|
||
最后,**让程序自动切换主节点**,这就需要其余正常运行的节点,来选择一个新的主节点,这样就回到了 Leader 选举的场景,分布式系统中的共识问题就出现了。这个方式是通过共识算法,让系统对一个新 Leader 节点达成共识,避免多个 Leader 节点出现,导致脑裂的情况发生。
|
||
|
||
到这里,我们就明白了,线性一致性是数据存储系统对外表现的一种形式,即好像只有一个数据副本,但是在实现数据一致性,实现容错的时候,我们需要共识算法的帮助。
|
||
|
||
当然,这里要特别注意,我们通过共识算法,除了可以实现线性一致性,也可以实现顺序一致性等其他的数据一致性,共识算法是用来满足线性一致性的容错性的。同时,不使用共识算法,我们也可以实现数据的线性一致性,比如 ABD 和 SCD broadcast 之类的非共识算法,也可以实现线性一致性。
|
||
|
||
总而言之,我们通过共识算法,可以实现高可用的线性一致性,以及其他的一致性存储系统,在这种情况下,**共识算法是手段,一致性是目的,先有共识算法,后有高可用的线性一致性系统**。同时,不通过共识算法,我们也可以用其他的方法,来实现线性一致性等其他的一致性,在这种情况下,共识和一致性就没有关系了。**不过,目前通过共识算法,来实现高可用的线性一致性模型,是一个最常见的选择**。
|
||
|
||
## 总结
|
||
|
||
本节课中,我们通过 Leader 选举的业务场景,讨论了共识问题的定义,并且得出了一个共识算法需要满足四个要求:一致同意、诚实性、合法性和可终止性。现在,你不仅可以识别出业务场景中的共识问题,还能深刻理解这些场景需要引入共识的原因。
|
||
|
||
接着,我们一起分析了达成共识所面临的挑战,其中让人震惊的是“ FLP 不可能”原理竟然证明了,在异步网络中,如果一个节点出现故障,共识就不可能达成。不过这种理论上的不可能,我们可以在现实中通过超时等机制解决。同时,我们还讨论了分布式系统中的几种故障模型,这让我们可以更好地理解分布式理论的研究对象,以及现实的分布式系统所面临的问题。
|
||
|
||
最后,我们讨论了一致性和共识的关系,得出了具体结论:通过共识算法,我们可以实现高可用的线性一致性,但是共识算法不是线性一致性的必要条件。到这里,你一定对一致性和共识有了清晰的认识。
|
||
|
||
## 思考题
|
||
|
||
本课中,我们明白了一致性和共识的关系,请你继续思考一下,共识和高可用之间有什么关系呢?
|
||
|
||
欢迎你在留言区发表你的看法。如果这节课对你有帮助,也推荐你分享给更多的同事、朋友。
|
||
|