16 KiB
15 | 最近邻检索(上):如何用局部敏感哈希快速过滤相似文章?
你好,我是陈东。
在搜索引擎和推荐引擎中,往往有很多文章的内容是非常相似的,它们可能只有一些修饰词不同。如果在搜索结果或者推荐结果中,我们将这些文章不加过滤就全部展现出来,那用户可能在第一页看到的都是几乎相同的内容。这样的话,用户的使用体验就会非常糟糕。因此,在搜索引擎和推荐引擎中,对相似文章去重是一个非常重要的环节。
对相似文章去重,本质上就是把相似的文章都检索出来。今天,我们就来聊聊如何快速检索相似的文章。
如何在向量空间中进行近邻检索?
既然是要讨论相似文章的检索,那我们就得知道,一篇文章是怎么用计算机能理解的形式表示出来的,以及怎么计算两篇文章的相似性。最常见的方式就是使用向量空间模型(Vector Space Model)。所谓向量空间模型,就是将所有文档中出现过的所有关键词都提取出来。如果一共有n个关键词,那每个关键词就是一个维度,这就组成了一个n维的向量空间。
那一篇文档具体该如何表示呢?我们可以假设,一篇文章中有k(0<k<=n)个关键词,如果第k个关键词在这个文档中的权重是w,那这个文档在第k维上的值就是w。一般来说,我们会以一个关键词在这篇文档中的TF-IDF值作为w的值。而如果文章不包含第k个关键词,那它在第k维上的值就是0,那我们也可以认为这个维度的权重就是0。这样,我们就可以用一个n维的向量来表示一个文档了,也就是<w1,w2,w3,……wn>。这样一来,每一个文档就都是n维向量空间中的一个点。
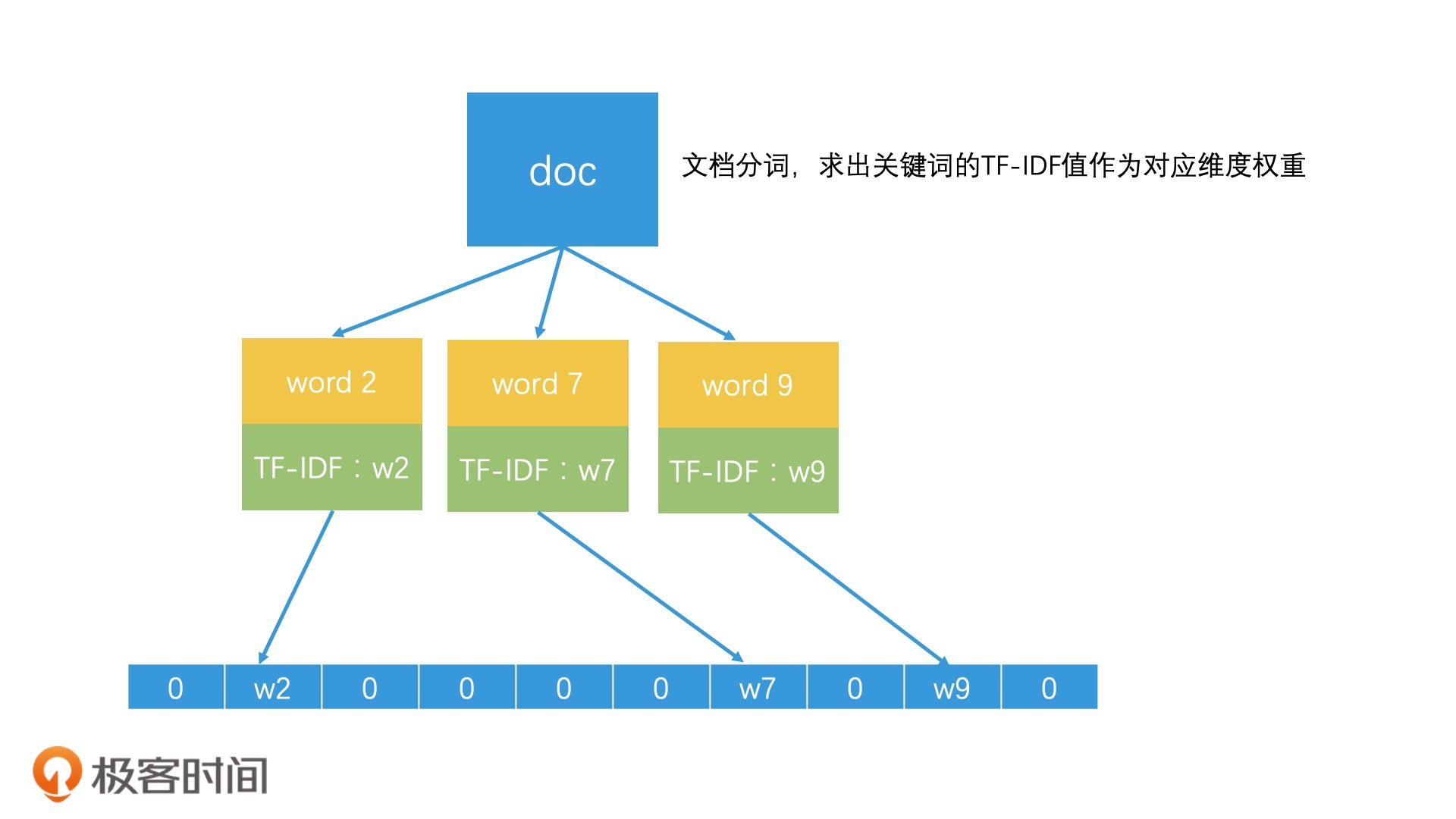
那接下来,计算两个文章相似度就变成了计算两个向量的相似度。计算向量相似度实际上就是计算两个向量的距离,距离越小,它们就越相似。具体在计算的时候,我们可以使用很多种距离度量方式。比如说,我们可以采用余弦距离,或者采用欧氏距离等。一般来说,我们会采用余弦距离来计算向量相似度。
拓展到搜索引擎和推荐引擎中,因为每个文档都是n维向量中的一个点,所以查询相似文章的问题,就变成了在n维空间中,查询离一个点距离最近的k个点的问题。如果把这些“点”想象成“人”,这不就和我们在二维空间中查询附近的人的问题非常类似了吗?这就给了我们一个启发,我们是不是也能用类似的检索技术来解决它呢?下面,我们一起来看一下。
首先,在十几维量级的低维空间中,我们可以使用k-d树进行k维空间的近邻检索,它的性能还是不错的。但随着维度的增加, 如果我们还要精准找到最邻近的k个点,k-d需要不停递归来探索邻接区域,检索效率就会急剧下降,甚至接近于遍历代价。当关键词是几万乃至百万级别时,文档的向量空间可能是一个上万维甚至是百万维的超高维空间,使用k-d树就更难以完成检索工作了。因此,我们需要寻找更简单、高效的方案。
这个时候,使用非精准Top K检索代替精准Top K检索的方案就又可以派上用场了。这是为什么呢?因为高维空间本身就很抽象,在用向量空间中的一个点表示一个对象的过程中,如果我们选择了不同的权重计算方式,那得到的向量就会不同,所以这种表示方法本身就已经损失了一定的精确性。
因此,对于高维空间的近邻检索问题,我们可以使用近似最近邻检索(Approximate Nearest Neighbor)来实现。你可以先想一想查询附近的人是怎么实现的,然后再和我一起来看高维空间的近似最近邻检索是怎么做的。
什么是局部敏感哈希?
借助非精准检索的思路,我们可以将高维空间的点也进行区域划分,然后为每个区域都生成一个简单的一维编码。这样,当我们要查找一个点最邻近的k个点的时候,直接计算出区域编码就能高效检索出同一个区域的所有对象了。
也因此,我们就能得出一个结论,那就是同一个区域中的不同的点,通过统一的计算过程,都能得到相同的区域编码。这种将复杂对象映射成简单编码的过程,是不是很像哈希的思路?
所以,我们可以利用哈希的思路,将高维空间中的点映射成低维空间中的一维编码。换句话说,我们通过计算不同文章的哈希值,就能得到一维哈希编码。如果两篇文章内容100%相同,那它们的哈希值就是相同的,也就相当于编码相同。
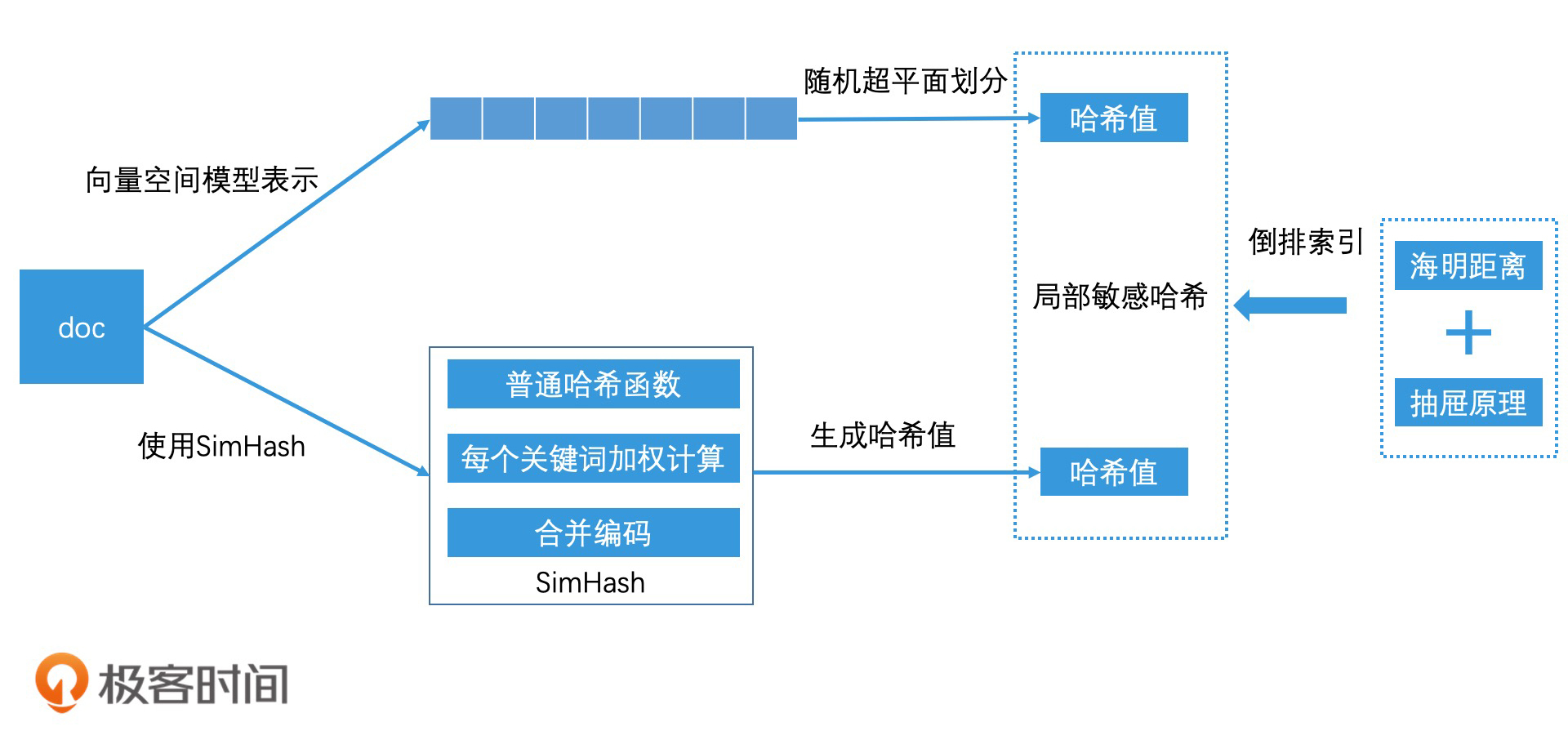
不过,如果我们用的是普通的哈希函数,只要文档中的关键词有一些轻微的变化(如改变了一个字),哈希值就会有很大的差异。但我们又希望,整体相似度高的两篇文档,通过哈希计算以后得到的值也是相近的。因此,工业界设计了一种哈希函数,它可以让相似的数据通过哈希计算后,生成的哈希值是相近的(甚至是相等的)。这种哈希函数就叫作局部敏感哈希(Locality-Sensitive Hashing)。
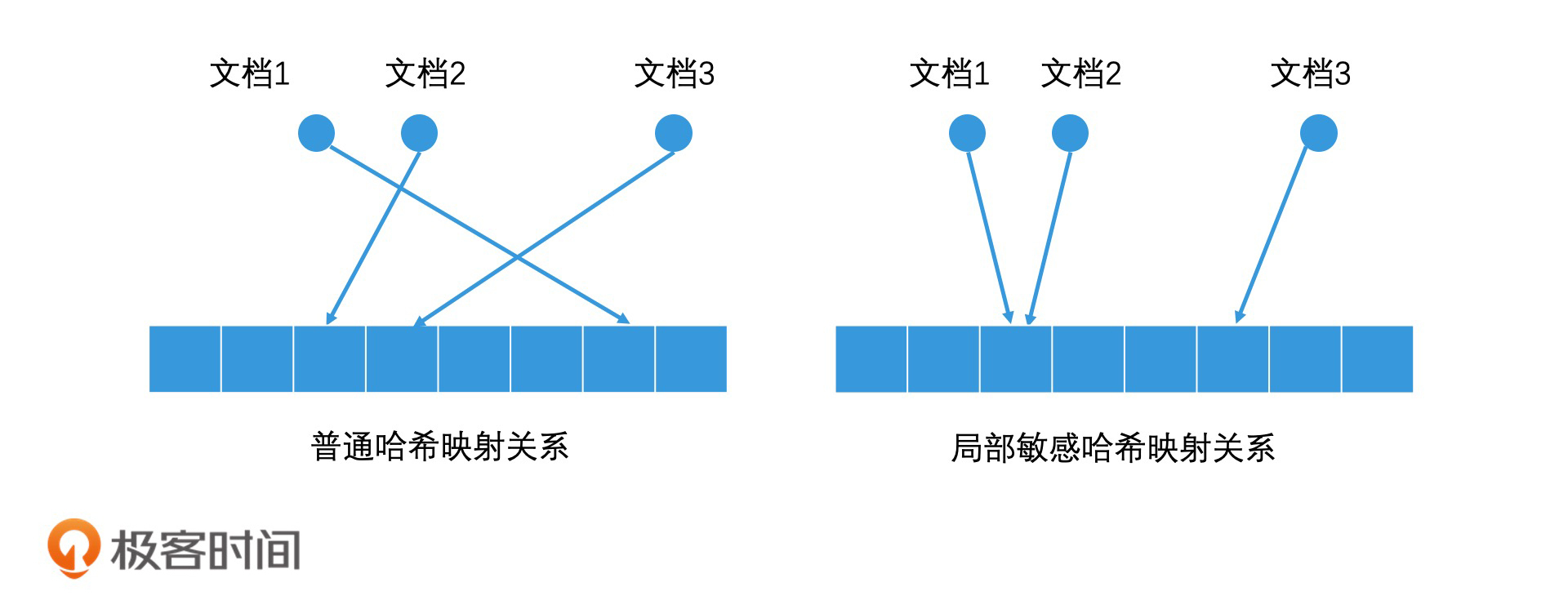
其实局部敏感哈希并不神秘。让我们以熟悉的二维空间为例来进一步解释一下。
在二维空间中,我们随意划一条直线就能将它一分为二,我们把直线上方的点的哈希值定为1,把直线下方的点的哈希值定为0。这样就完成一个简单的哈希映射。通过这样的随机划分,两个很接近的点被同时划入同一边的概率,就会远大于其他节点。也就是说,这两个节点的哈希值相同的概率会远大于其他节点。
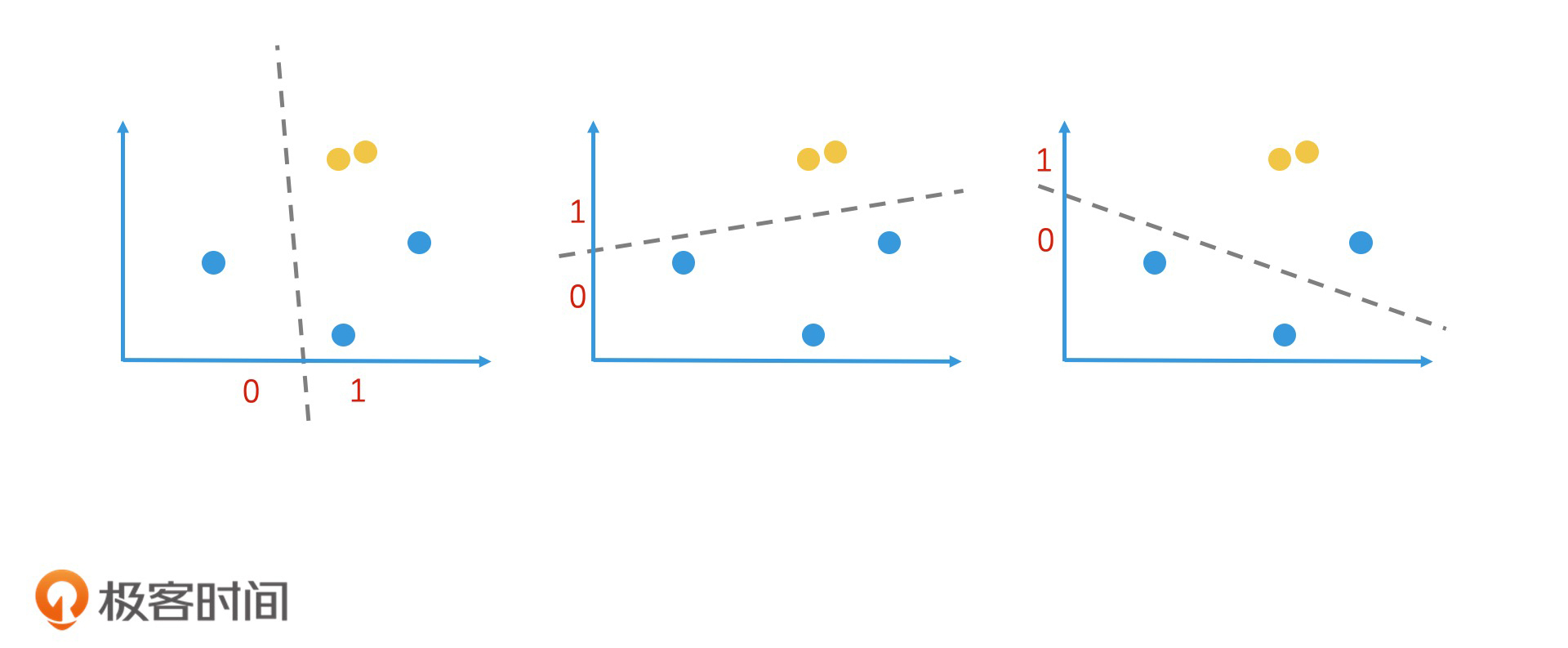
当然,这样的划分有很大的随机性,不一定可靠。但是,如果我们连续做了n次这样的随机划分,这两个点每次都在同一边,那我们就可以认为它们在很大概率上是相近的。因此,我们只要在n次随机划分的过程中,记录下每一个点在每次划分后的值是0还是1,就能得到一个n位的包含0和1的序列了。这个序列就是我们得到的哈希值,也就是区域编码。
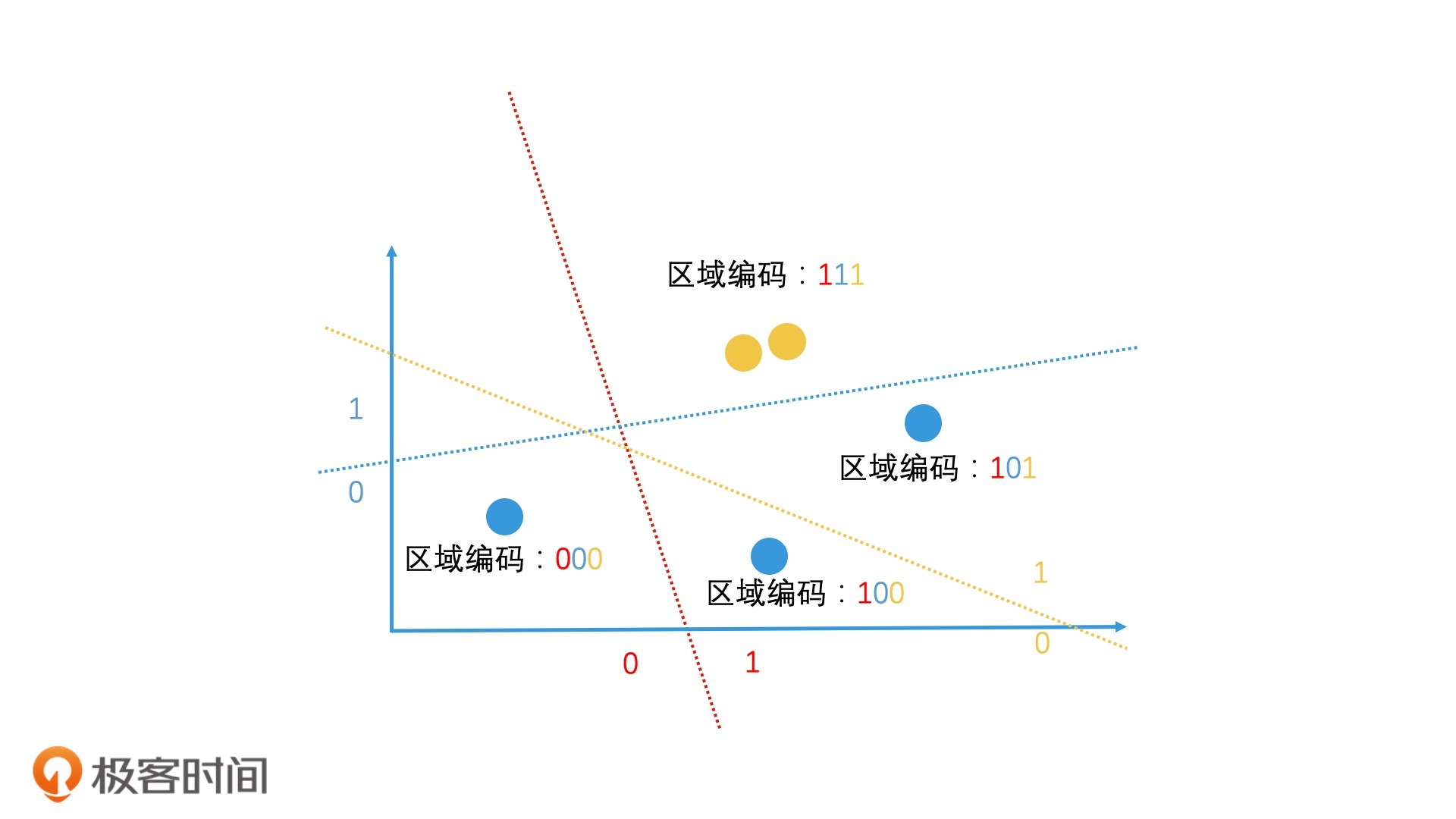
因此,对于高维空间,我们构造局部敏感哈希函数的方案是,随机地生成n个超平面,每个超平面都将高维空间划分为两部分。位于超平面上面的点的哈希值为1,位于超平面下方的点的哈希值为0。由于有n个超平面,因此一个点会被判断n次,生成一个n位的包含0和1的序列,它就是这个点的哈希值。这就是一个基于超平面划分的局部敏感哈希构造方法。(为了方便你直观理解,我简单说成了判断一个点位于超平面的上面还是下面。在更严谨的数学表示中,其实是求一个点的向量和超平面上法向量的余弦值,通过余弦值的正负判断是1还是0。这里,你理解原理就可以了,严谨的数学分析我就不展开了。)
如果有两个点的哈希值是完全一样的,就说明它们被n个超平面都划分到了同一边,它们有很大的概率是相近的。即使哈希值不完全一样,只要它们在n个比特位中有大部分是相同的,也能说明它们有很高的相近概率。
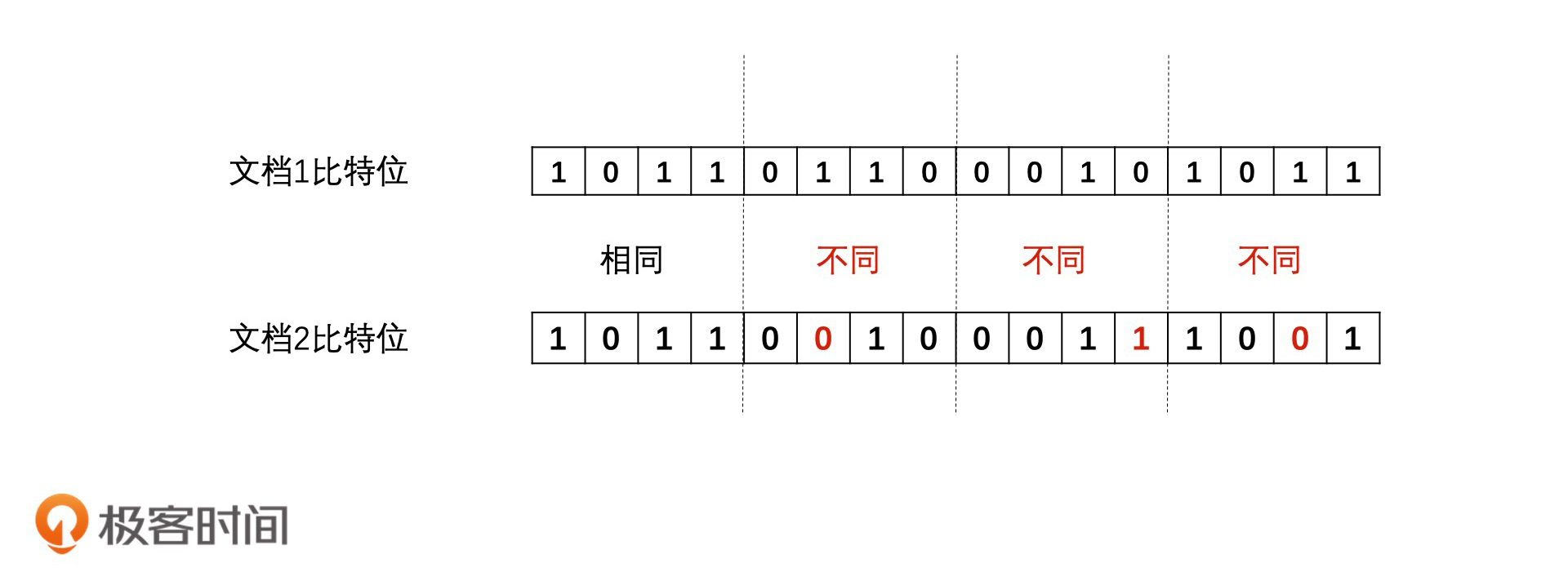
上面我们说的判断标准都比较笼统,实际上,在利用局部敏感哈希值来判断文章相似性的时候,我们会以表示比特位差异数的海明距离(Hamming Distance)为标准。我们可以认为如果两个对象的哈希值的海明距离低于k,它们就是相近的。举个例子,如果有两个哈希值,比特位分别为00000和10000。你可以看到,它们只有第一个比特位不一样,那它们的海明距离就是1。如果我们认为海明距离在2之内的哈希值都是相似的,那它们就是相似的。
SimHash是怎么构造的?
不过,这种构造局部敏感哈希函数的方式也有一些缺陷:在原来的空间中,不同维度本来是有着不同权重的,权重代表了不同关键词的重要性,是一个很重要的信息。但是空间被n个超平面随机划分以后,权重信息在某种程度上就被丢弃了。
那为了保留维度上的权重,并且简化整个函数的生成过程,Google提出了一种简单有效的局部敏感哈希函数,叫作SimHash。它其实是使用一个普通哈希函数代替了n次随机超平面划分,并且这个普通哈希函数的作用对象也不是文档,而是文档中的每一个关键词。这样一来,我们就能在计算的时候保留下关键词的权重了。这么说有些抽象,让我们一起来看看SimHash的实现细节。
方便起见,我们就以Google官方介绍的64位的SimHash为例,来说一说它构造过程。整个过程,我们可以总结为5步。
- 选择一个能将关键词映射到64位正整数的普通哈希函数。
- 使用该哈希函数给文档中的每个关键词生成一个64位的哈希值,并将该哈希值中的0修改为-1。比如说,关键词A的哈希值编码为<1,0,1,1,0>,那我们做完转换以后,编码就变成了<1,-1,1,1,-1>。
- 将关键词的编码乘上关键词自己的权重。如果关键词编码为<1,-1,1,1,-1>,关键词的权重为2,最后我们得到的关键词编码就变成了<2,-2,2,2,-2>。
- 将所有关键词的编码按位相加,合成一个编码。如果两个关键词的编码分别为<2,-2,2,2,-2>和<3,3,-3,3,3>,那它们相加以后就会得到<5,1,-1,5,1>。
- 将最终得到的编码中大于0的值变为1,小于等于0的变为0。这样,编码<5,1,-1,5, 1>就会被转换为<1,1,0,1,1>。
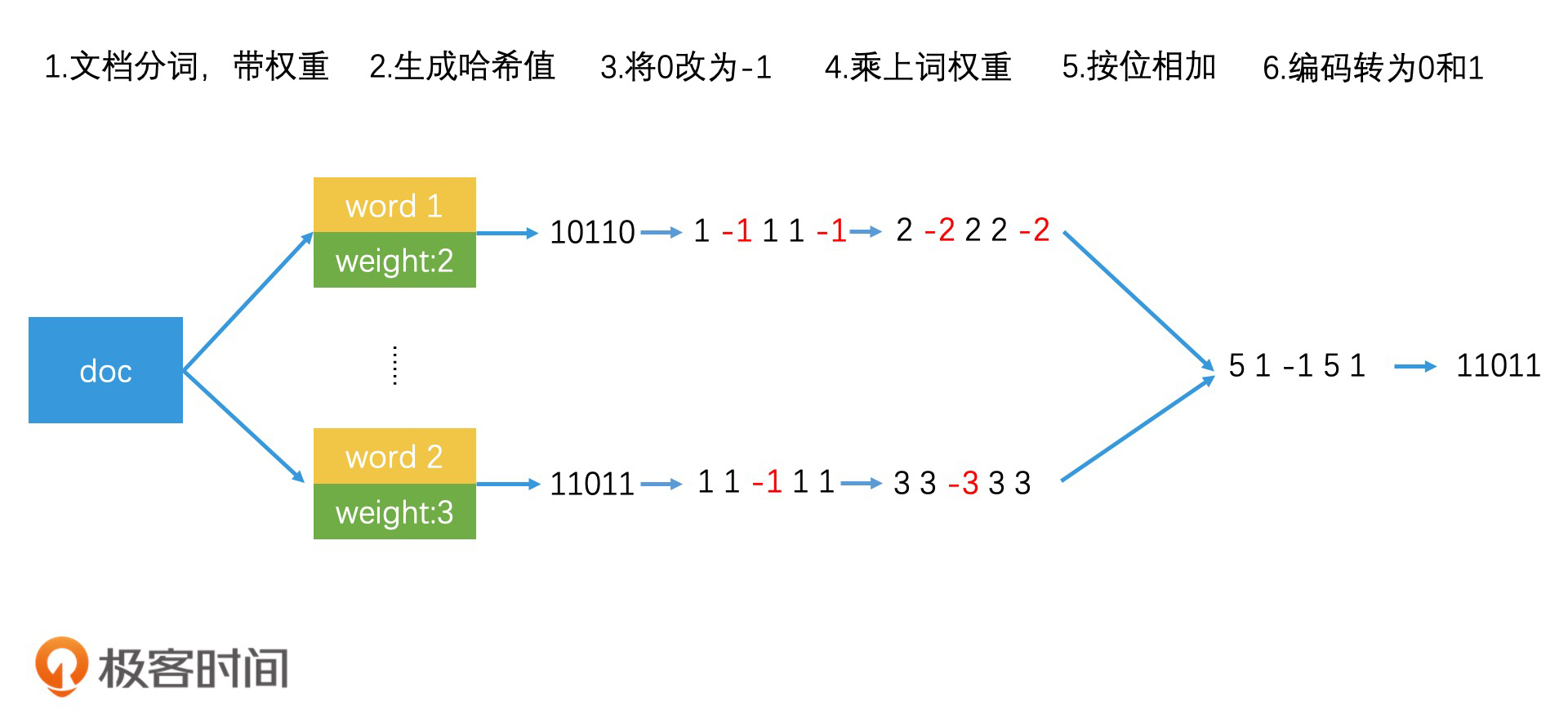
通过这样巧妙的构造,SimHash将每个关键词的权重保留并且叠加,一直留到最后,从而使得高权重的关键词的影响能被保留。从上图中你可以看到,整个文档的SimHash值和权重最大的关键词word 2的哈希值是一样的。这就体现了高权重的关键词对文档的最终哈希值的影响。此外,SimHash通过一个简单的普通哈希函数就能生成64位哈希值,这替代了随机划分64个超平面的复杂工作,也让整个函数的实现更简单。
如何对局部敏感哈希值进行相似检索?
和其他局部敏感哈希函数一样,如果两个文档的SimHash值的海明距离小于k,我们就认为它们是相似的。举个例子,在Google的实现中,k的取值为3。这个时候,检索相似文章的问题变成了要找出海明距离在3之内的所有文档。如果是一个个文档比对的话,这就是一个遍历过程,效率很低。有没有更高效的检索方案呢?
一个直观的想法是,我们可以针对每一个比特位做索引。由于每个比特位只有0和1这2个值,一共有64个比特位,也就一共有2*64共128个不同的Key。因此我们可以使用倒排索引,将所有的文档根据自己每个比特位的值,加入到对应的倒排索引的posting list中。这样,当要查询和一个文档相似的其他文档的时候,我们只需要通过3步就可以实现了,具体的步骤如下:
- 计算出待查询文档的SimHash值;
- 以该SimHash值中每个比特位的值作为Key,去倒排索引中查询,将相同位置具有相同值的文档都召回;
- 合并这些文档,并一一判断它们和要查询的文档之间的海明距离是否在3之内,留下满足条件的。
我们发现,在这个过程中,只要有一个比特位的值相同,文档就会被召回。也就是说,这个方案和遍历所有文档相比,其实只能排除掉“比特位完全不同的文档”。因此,这种方法的检索效率并不高。
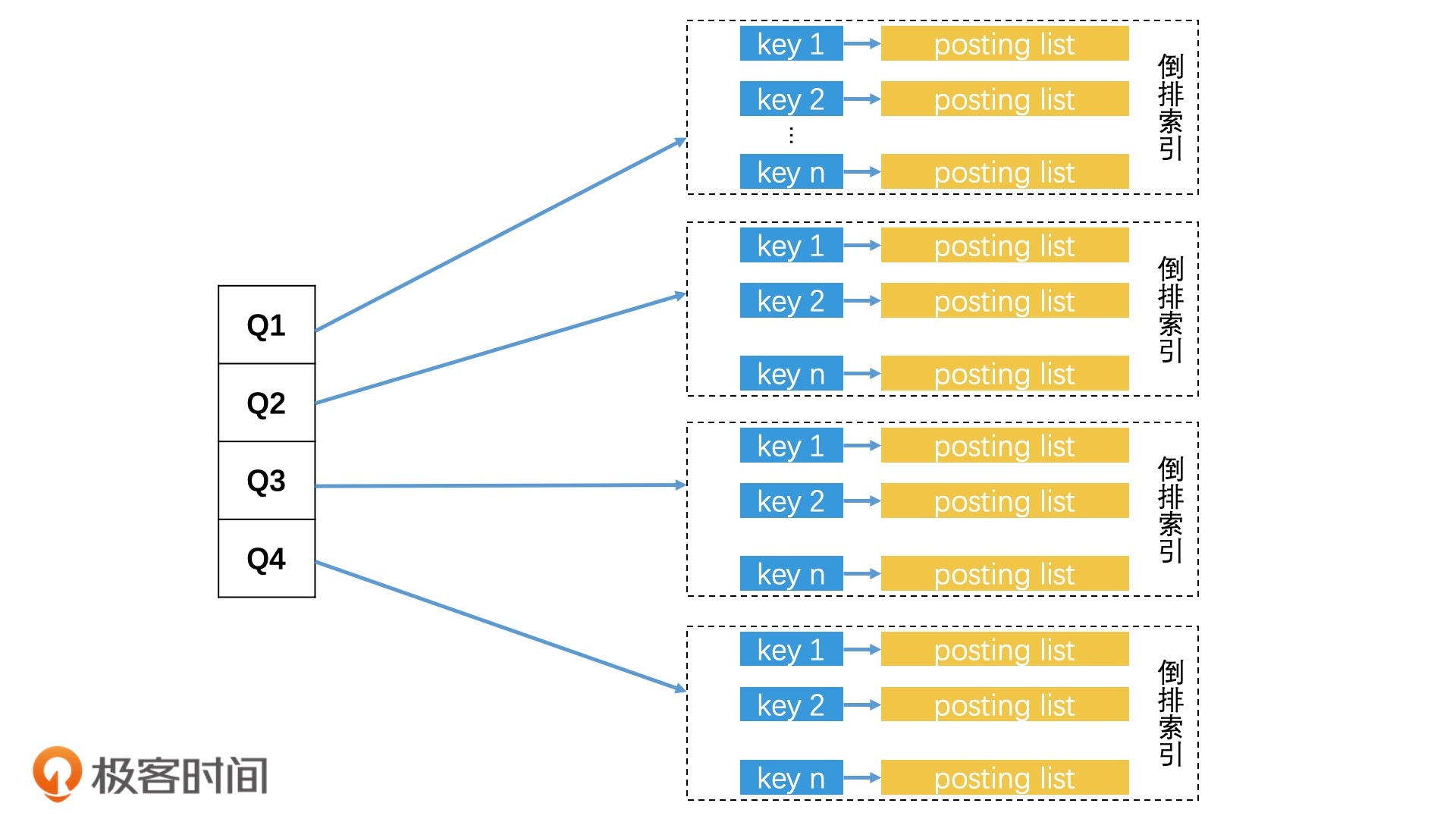
这又该怎么优化呢?Google利用抽屉原理设计了一个更高效的检索方法。什么是抽屉原理呢?简单来说,如果我们有3个苹果要放入4个抽屉,就至少有一个抽屉会是空的。那应用到检索上,Google会将哈希值平均切为4段,如果两个哈希值的比特位差异不超过3个,那这三个差异的比特位最多出现在3个段中,也就是说至少有一个段的比特位是完全相同的!因此,我们可以将前面的查询优化为“有一段比特位完全相同的文档会被召回”。
根据这个思路,我们可以将每一个文档都根据比特位划分为4段,以每一段的16个比特位的值作为Key,建立4个倒排索引。检索的时候,我们会把要查询文档的SimHash值也分为4段,然后分别去对应的倒排索引中,查询和自己这一段比特位完全相同的文档。最后,将返回的四个posting list合并,并一一判断它们的的海明距离是否在3之内。
通过使用SimHash函数和分段检索(抽屉原理),使得Google能在百亿级别的网页中快速完成过滤相似网页的功能,从而保证了搜索结果的质量。
重点回顾
今天,我们重点学习了使用局部敏感哈希的方法过滤相似文章。
我们可以使用向量空间模型将文章表示为高维空间中的点,从而将相似文章过滤问题转为高维空间的最近邻检索问题。对于高维空间的最近邻检索问题,我们可以使用非精准的检索思路,使用局部敏感哈希为高维空间的点生成低维的哈希值。
局部敏感哈希有许多构造方法,我们主要讲了随机超平面划分和SimHash两种方法。相比于随机超平面划分,SimHash能保留每一个关键词的权重,并且它的函数实现也更简单。
那对于局部敏感哈希的相似检索,我们可以使用海明距离定义相似度,用抽屉原理进行分段划分,从而可以建立对应的倒排索引,完成高效检索。
实际上,不仅过滤相似文章可以使用局部敏感哈希,在拍照识图和摇一摇搜歌等应用场景中,我们都可以使用它来快速检索。以图像检索为例,我们可以对图像进行特征分析,用向量来表示一张图片,这样一张图片就是高维空间中的一个点了,图像检索就也抽象成了高维空间中的近邻检索问题,也就可以使用局部敏感哈希来完成了。
当然基于局部敏感哈希的检索也有它的局限性。以相似文章检索为例,局部敏感哈希更擅长处理字面上的相似而不是语义上的相似。比如,一篇文章介绍的是随机超平面划分,另一篇文章介绍的是SimHash,两篇文章可能在字面上差距很大,但内容领域其实是相似的。好的推荐系统在用户看完随机超平面划分的文章后,还可以推荐SimHash这篇文章,但局部敏感哈希在这种语义相似的推荐系统中就不适用了。
因此,对于更灵活的相似检索问题,工业界还有许多的解决方法,我们后面再详细介绍。
课堂讨论
1.对于SimHash,如果将海明距离在4之内的文章都定义为相似的,那我们应该将哈希值分为几段进行索引和查询呢?
2.SimHash的算法能否应用到文章以外的其他对象?你能举个例子吗?
欢迎在留言区畅所欲言,说出你的思考过程和最终答案。如果有收获,也欢迎把这一讲分享给你的朋友。