13 KiB
06 | 数据分布:房子应该是买贵的还是买便宜的?
数据给你一双看透本质的眼睛,这里是《数据分析思维课》,我是郭炜。
在上一节课里,我们聊了聊直方图和幂分布。其实一提到数据分布,你首先会想到过去在课堂上学的二次分布、柏松分布等等分布。学习的这些分布对你考试很有帮助,但是在生活当中我们其实用得不多。
其实在实际生活当中,我们最常见的是正态分布和拉普拉斯分布,这两个分布反映了现实生活当中隐藏在数据背后的“势”。了解这些数据的趋势,才可以让你更好地了解实际的工作和生活本身。
为什么说这两个分布会更实用呢?
比方说,一座城市的市民身高或者体重分布就是符合正态分布的。再比如说,极客时间所有用户的日均播放时长,它也会是一个正态分布的曲线。
正态分布既然这么常见,那么一个城市的房价也应该和这个城市市民的身高一样,是正态分布的。但现实往往是明明只隔了一条街,房价相差巨大,有的时候差价甚至会高达数倍。这就像100人里,突然出来10个姚明一样让人费解。这个时候,就轮到拉普拉斯分布出场了。
今天这节课,我就以正态分布和拉普拉斯分布为例,给你讲下数据分布以及怎样用数据分布理解我们生活和工作中的“大势”。
正态分布
我们先来看正态分布。正态分布就是你在课本里曾经学过的那个两头低、中间高然后左右轴对称的钟形曲线。最早用正态曲线描述数据的人,就是那位你我都熟知的德国著名数学家高斯,为了纪念他,有时候我们也把正态分布称为高斯分布。在德国,十马克的纸币上都留有高斯的头像和正态分布的曲线,如下图所示。
但正态分布这个名字不是高斯取的,而是由达尔文的表兄弟弗朗西斯·高尔顿命名。高尔顿开创了遗传学的统计研究,并用正态曲线来表明他的研究结果,这个名字后来广为流传。
学术上是这么来定义正态分布的:“如果一个量是由许多微小的独立随机因素影响的结果,那么就可以认为这个量具有正态分布”。听完这个定义,你能不能联想到我们前面讲的平均值和大数定律呢?
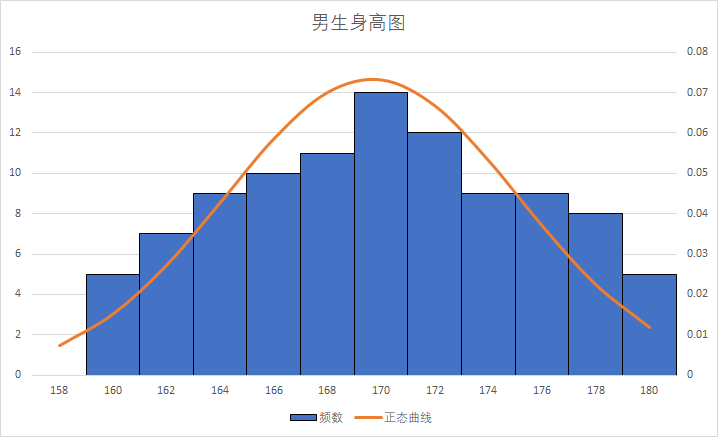
结合平均值和大数定律,我来给你举一个我们现实生活中的例子。比如我们知道中国人的平均身高大概是1米7,那么实际上我们随机找100个人,把每个区间的身高累个计数画出来一个直方图,它就会是一个正态曲线。
对这个曲线来说,他们平均值1米7就是最高的那个点,1米6几和1米7几的人数会分布在最高点的两侧。随着身高的增长或降低,人数会逐渐减少,最后就呈现出了钟形曲线两边的下降。
我们来看个具体运用正态分布的例子。比方领导说要访谈调研下用户整体对你的产品的反馈,于是你通过发调研问卷的方式,拿出100个调研结果给领导。但没想到领导说,你这太不专业了,都是片面回答,你要给我95%的准确率。你很委屈,你不知道多少人才会有代表性,才能达到领导要的95%准确率。
那么我们具体需要多大的人群来进行测试,才可以符合领导的要求呢?
答案是400人。具体推算的方法,你要是感兴趣可以参考这节课最后的附录部分,并自己动手来算一算。现在我先给你讲一下整体的推算思路:
- 由于我们选择的身高、A/B测试、用户反馈都是随机分布的(符合正态分布),所以我们可以用正态分布来进行推算;
- 领导说要95%正确率,其实就是说正态分布钟型曲线中间这个中段要95%,在计算的时候其实我们可以转换下思路,95%的正确率也就是指误差在5%以内。
- 紧接着我们套用附录公式,去查正态分布表进行计算后就可以得出结论。
你从附录的计算结果中可以看到,如果是要95%的正确率,那么需要385人参与测试。但是我们选人数一般不会这么有零有整,所以通常来说,选400人会比较合适。
如果你的调研还要针对地域、年龄再进行进一步的细分,你也可以通过正态分布来把它计算出来,不过你需要注意的是,你用于调研或者测试的样本就不是两种而会变成多种了。
我们要根据某一个数据进行运营估计的时候,也可以用到正态分布。
比如我们现在要根据极客时间用户每天收听音频的平均时长来打造一个用户等级,那这种用户等级分布和所需要的福利金额费用大概是什么样子呢?
其实只要我们算出来极客时间的每一个用户的日均平均时长(就是所谓的总体均值),再根据误差范围设定标准差,就可以根据随机抽样和中心极限定理,得出来每个不同等级的用户的数量。这样,我们做积分的估算补贴和使用的时候,心里就有数了。
我看到网上很多人都把中心极限定理和大数定律放到一起来谈,你可能听过这样一句话:“在随机原则下,当抽样数目足够多的时候,样本就会遵照大数定律而呈正态分布”,这其实是不对的。
大数定律研究的是随机变量序列依概率收敛到其均值的算术平均,说白了就是为了说明频率在概率附近摇摆,也为我们将频率当作概率提供了依据。
可能这么说还是有些绕,我拿抛骰子给你举个例子。在抛骰子这件事上,大数定律说的是只要你抛的次数足够多,骰子每一个面向上的概率应该都是1/6。
而中心极限定理要求的是独立随机样本,在中心极限定理下,随着样本数量趋于无穷大,独立随机样本和独立随机样本和的分布会越来越像正态分布。
还是用抛骰子的例子来给你解释一下中心极限定理。比如你抛6次骰子发现求和是18,你又抛6次发现加起来是20,你又抛了6次,这次发现加起来是25。如果你抛的次数足够多,你把18、20、25等这些数据画出一个图来,这个图是符合正态分布的。
所以大数定律和中心极限定理说的不是一个维度的事情。大数定律算的是概率,中心极限定理算的是样本和的分布。
拉普拉斯分布
还记得我们这节课开头提到的房价这件事吗?理论上房价应该和人的身高一样,在某一个地区有一个均价,并且整体的房价和身高是一样呈正态分布。但为什么在某一个区域可能就隔了一条街,房价却翻了好几倍,而且数量也不少?这不符合刚刚说的中心极限定理呀。
关于这个问题,我的答案是:我们的房价其实和我们的身高是不一样的,它不是我们想象当中的正态分布,而是我下面提到的拉普拉斯分布。
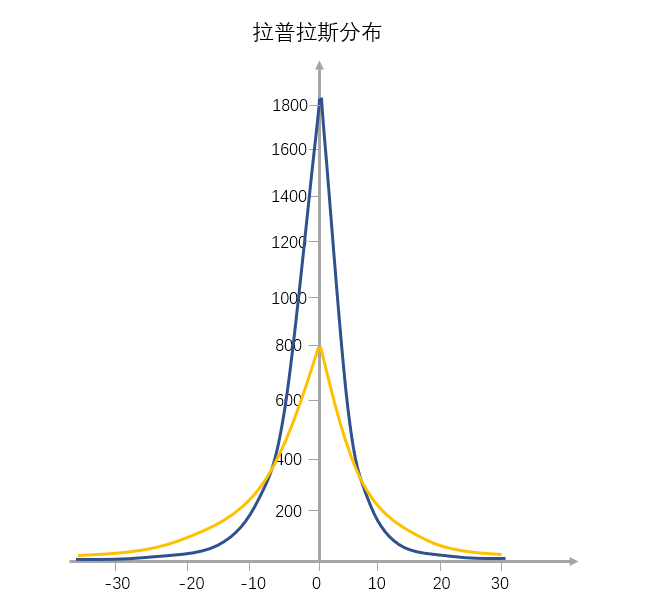
拉普拉斯分布就和上图一样,是一个“凸”字形的塔尖儿曲线,从左到右,斜率先缓慢增大再快速增大,到达最高点后变为负值继续先快速减小,最后再缓慢地减小,所以有点像“往里边凹陷的金字塔”。
对比正态分布的概率密度函数图像,我们可以看到拉普拉斯分布图像是尖峰厚尾的,塔尖上的那些,就是我们看到的稀缺资源。比如拿全球顶尖程序员的薪资(塔尖对应的横坐标值是均值)来说,全球顶尖的程序员年薪是100万美元,但这部分群体可能只占全球城市人口的1%,程序员中的人数不足10%。但是,90%的资源其实都在他们的身上,够刺激吧。
那我们怎样去理解这个拉普拉斯分布呢?它经常用在金融领域,尤其是衡量股票收益的时候。起初我们认为股票收益率是服从正态分布,但是由于股票价格波动与时间变化有关,有波动聚集性,最后实际股票的收益率都是符合拉普拉斯分布的,也就是赚大钱的日子其实特别集中,余下的都是赚小钱的日子。
现在随着市场和互联网的发展,信息越来越透明,我们相关的数据分布其实变化还是挺大的。
比如说在改革开放之前信息不对称,资源也相对没有那么聚集,人们拿到的工资是一个正态分布的。但是到了现在,就我们程序员的工资来说,一个顶尖的程序员和普通的程序员的工资收入可能会差十倍都不止,这就会导致更厚的尾部和更高的峰度。
而全国的城市房价分布、一个城市当中的小区房价分布现在也是符合拉普拉斯分布的。因为在信息透明和市场竞争的情况下,工资、房价、股票都会符合一个特点:**越塔尖的个体越具有资源吸附能力。**那么在整体资源恒定的情况下,这已经不是一个简单的符合随机分布的市场了,简单来讲,“大势”变了。
所以当你在做数据分析的时候,一定得先考虑一下,原有的数据分布模型是否还适用于现有的市场情况?
准确把握住数据分布这个大势,我们才能够做出更为正确的决策。就拿买房这件事来说吧,买房是一个我们基本都绕不开的话题,在你买房前,你可以先判断一下你要买的房屋的房价在这座城市里是正态分布还是拉普拉斯分布。
也就是说你可以去评估一下,你所在城市资源是否比较平均?会不会出现聚集效应?如果你认真用这两个分布去判断一下,你会发现如果你所在的城市是三四线城市,那么房价的分布大概率会呈正态分布。那么在这种情况下你要投资买房就可以选择价格在曲线腰部的房子,这种房子的房价将来涨跌以及抗风险性都比较适中。
而如果你准备买大城市里的房子,情况就不一样了。因为对于一线城市的房价而言,大概率是呈拉普拉斯分布的,这也就意味着越贵的房子周边资源越好,进而这些房子将来增值空间越大。那我们买房子的时候就应该买资源最好的最贵的房子,未来的收获也最大(当然,如果最贵的已经天价了,那么我们可以退而求其次)。
反之,当你看到一些铺面房非常便宜的时候,你要留个心眼了:是不是这些铺面房处于拉普拉斯分布的最两侧?如果是,那么这些铺面房不但增值空间小,将来还有可能买了亏本的风险。所以,只有了解整体市场的分布我们才能够更好地把握市场大势,顺势而为。
小结
好了,这节课到这里也就接近尾声了。最后我来给你总结一下这节课的要点。
今天我给你讲了正态分布和拉普拉斯分布,这是我们在现实生活当中最常用到的两个分布。希望这两个分布能够帮助你分析工作生活里数据背后的“势”,做好对生活、工作的决策。
将来无论在什么场景下做数据分析,数据的分布应该能贴合地描述我们社会上的“大势”,所以当你面临生活中的决策时,而不能就数据套数据、为了算法而算法,领域背后的知识对于我们更加重要。
就像今天我给你讲的正态分布和拉普拉斯分布的例子一样,现如今我们的生活中,有的事物符合正态分布,有的事物符合拉普拉斯分布。就比如说我们在买房的时候,没有判断好我们所处城市的房价到底是正态分布还是拉普拉斯分布,很有可能会导致你错误的投资决策。
更进一步来说,这两个数据分布其实给我们的工作生活也有一个大的启示,那就是为什么会有这样一句话的流行:“Work Hard, Play Hard”,因为这句话背后的含义其实是指当你要获得更多的自由的时候,你也要付出同等的甚至更多的自律(控制自己既能使劲玩也能使劲工作)。当今社会的人才分布是呈拉普拉斯分布的,我们要争取做顶尖,这样才会有更多的资源和机会。
数据给你一双看透本质的眼睛,我们要持续努力学习,一起共勉!
课后思考
在你工作和生活当中,你遇到的哪些事情的分布是正态分布,哪些是拉普拉斯分布?遇到这些数据分布的情况的时候,你应该做些什么?欢迎你留言我们一起讨论。
附录:A/B测试需要多少人才有意义的推算
我把推算的过程做成了图片的形式,你可以长按保存,然后打印下来,对照着自己用笔算一算。