156 lines
11 KiB
Markdown
156 lines
11 KiB
Markdown
# 10 | 那些在Netflix Prize中大放异彩的推荐算法
|
||
|
||
早在前几篇务虚的文章中,我就和你聊过了推荐系统中的经典问题,其中有一类就是评分预测。
|
||
|
||
让我摸着自己的良心说,评分预测问题只是很典型,其实并不大众,毕竟在实际的应用中,评分数据很难收集到,属于典型的精英问题;与之相对的另一类问题行为预测,才是平民级推荐问题,处处可见。
|
||
|
||
## 缘起
|
||
|
||
评分预测问题之所以“虽然小众却十分重要”,这一点得益于十多年前 Netflix Prize 的那一百万美元的悬赏效应。
|
||
|
||
公元2006年10月2号,对于很多人来说,这只是平凡了无新意的一天,但对于推荐系统从业者来说,这是不得了的一天,美国著名的光盘租赁商 Netflix 突然广发英雄帖,放下“豪”言,这个就是土豪的“豪”,凡是能在他们现有推荐系统基础上,把均方根误差降低10%的大侠,可以瓜分100万美元。消息一出,群贤毕至。
|
||
|
||
Netflix放出的比赛数据,正是评分数据,推荐系统的问题模式也是评分预测,也就是为什么说,评价标准是均方根误差了。
|
||
|
||
这一评分预测问题在一百万美元的加持下,催生出无数推荐算法横空出世,其中最为著名的就是一系列矩阵分解模型,而最最著名的模型就是SVD以及其各种变体。这些模型后来也经受了时间检验,在实际应用中得到了不同程度的开枝散叶。
|
||
|
||
今天我就来和你细聊一下矩阵分解,SVD及其最有名的变种算法。
|
||
|
||
## 矩阵分解
|
||
|
||
### 为什么要矩阵分解
|
||
|
||
聪明的你也许会问,好好的近邻模型,一会儿基于用户,一会儿基于物品,感觉也能很酷炫地解决问题呀,为什么还要来矩阵分解呢?
|
||
|
||
刨除不这么做就拿不到那一百万的不重要因素之外,矩阵分解确实可以解决一些近邻模型无法解决的问题。
|
||
|
||
我们都是读书人,从不在背后说模型的坏话,这里可以非常坦诚地说几点近邻模型的问题:
|
||
|
||
1. 物品之间存在相关性,信息量并不随着向量维度增加而线性增加;
|
||
2. 矩阵元素稀疏,计算结果不稳定,增减一个向量维度,导致近邻结果差异很大的情况存在。
|
||
|
||
上述两个问题,在矩阵分解中可以得到解决。矩阵分解,直观上说来简单,就是把原来的大矩阵,近似分解成两个小矩阵的乘积,在实际推荐计算时不再使用大矩阵,而是使用分解得到的两个小矩阵。
|
||
|
||
具体说来就是,假设用户物品的评分矩阵A是m乘以n维,即一共有m个用户,n个物品。我们选一个很小的数k,这个k比m和n都小很多,比如小两个数量级这样,通过一套算法得到两个矩阵U和V,矩阵U的维度是m乘以k,矩阵V的维度是n乘以k。
|
||
|
||
这两个矩阵有什么要求呢?要求就是通过下面这个公式复原矩阵A,你可以点击文稿查看公式。
|
||
|
||
$$ U\_{m\\times{k}}V\_{n\\times{k}}^{T} \\approx A\_{m\\times{n}}$$
|
||
|
||
类似这样的计算过程就是矩阵分解,还有一个更常见的名字叫做SVD;但是,SVD和矩阵分解不能划等号,因为除了SVD还有一些别的矩阵分解方法。
|
||
|
||
### 1 基础的SVD算法
|
||
|
||
值得一说的是,SVD全称奇异值分解,属于线性代数的知识;然而在推荐算法中实际上使用的并不是正统的奇异值分解,而是一个伪奇异值分解(具体伪在哪不是本文的重点)。
|
||
|
||
今天我介绍的SVD是由Netflix Prize中取得骄人成绩的Yehuda Koren提出的矩阵分解推荐算法。
|
||
|
||
按照顺序,首先介绍基础的SVD算法,然后是考虑偏置信息,接着是超越评分矩阵增加多种输入,最后是增加时间因素。好,一个一个来。
|
||
|
||
前面已经从直观上大致说了矩阵分解是怎么回事,这里再从物理意义上解释一遍。矩阵分解,就是把用户和物品都映射到一个k维空间中,这个k维空间不是我们直接看得到的,也不一定具有非常好的可解释性,每一个维度也没有名字,所以常常叫做隐因子,代表藏在直观的矩阵数据下面的。
|
||
|
||
每一个物品都得到一个向量q,每一个用户也得到一个向量p。对于物品,与它对应的向量q中的元素,有正有负,代表着这个物品背后暗藏的一些用户关注的因素。
|
||
|
||
对于用户,与它对应的向量p中的元素,也有正有负,代表这个用户在若干因素上的偏好。物品被关注的因素,和用户偏好的因素,它们的数量和意义是一致的,就是我们在矩阵分解之处人为指定的k。
|
||
|
||
举个例子,用户u的向量是pu,物品i的向量是qi,那么,要计算物品i推荐给用户u的推荐分数,直接计算点积即可:
|
||
|
||
$$ \\hat{r}\_{ui} = p\_{u}q\_{i}^{T}$$
|
||
|
||
看上去很简单,难在哪呢?难在如何得到每一个用户,每一个物品的k维向量。这是一个机器学习问题。按照机器学习框架,一般就是考虑两个核心要素:
|
||
|
||
1. 损失函数;
|
||
2. 优化算法。
|
||
|
||
SVD的损失函数是这样定义的:
|
||
|
||
$$ \\min\_{q^{\* },p^{\* } } \\sum\_{(u,i) \\in \\kappa }{(r\_{ui} - p\_{u}q\_{i}^{T})^{2} + \\lambda (||q\_{i}||^{2} + ||p\_{u}||^{2})} $$
|
||
|
||
理解SVD的参数学习过程并不是必须的,如果你不是算法工程师的话不必深究这个过程。
|
||
|
||
由于这个公式略复杂,如果你正在听音频,就需要自己看一下图片。这个损失函数由两部分构成,加号前一部分控制着模型的偏差,加号后一部分控制着模型的方差。
|
||
|
||
前一部分就是:用分解后的矩阵预测分数,要和实际的用户评分之间误差越小越好。
|
||
|
||
后一部分就是:得到的隐因子向量要越简单越好,以控制这个模型的方差,换句话说,让它在真正执行推荐任务时发挥要稳定。这部分的概念对应机器学习中的过拟合,有兴趣可以深入了解。
|
||
|
||
整个SVD的学习过程就是:
|
||
|
||
1. 准备好用户物品的评分矩阵,每一条评分数据看做一条训练样本;
|
||
2. 给分解后的U矩阵和V矩阵随机初始化元素值;
|
||
3. 用U和V计算预测后的分数;
|
||
4. 计算预测的分数和实际的分数误差;
|
||
5. 按照梯度下降的方向更新U和V中的元素值;
|
||
6. 重复步骤3到5,直到达到停止条件。
|
||
|
||
过程中提到的梯度下降是优化算法的一种,想深入了解可以参见任何一本机器学习的专著。
|
||
|
||
得到分解后的矩阵之后,实质上就是得到了每个用户和每个物品的隐因子向量,拿着这个向量再做推荐计算就简单了,哪里不会点哪里,意思就是拿着物品和用户两个向量,计算点积就是推荐分数了。
|
||
|
||
### 2 增加偏置信息
|
||
|
||
到现在,你已经知道基础的SVD是怎么回事了。现在来多考虑一下实际情况,试想一下:有一些用户会给出偏高的评分,比如标准宽松的用户;有一些物品也会收到偏高的评分,比如一些目标观众为铁粉的电影,甚至有可能整个平台的全局评分就偏高。
|
||
|
||
所以,原装的SVD就有了第一个变种:把偏置信息抽出来的SVD。
|
||
|
||
一个用户给一个物品的评分会由四部分相加:
|
||
|
||
$$\\hat{r}\_{ui} = \\mu + b\_{i} + b\_{u} + p\_{u}q\_{i}^{T} $$
|
||
|
||
从左至右分别代表:全局平均分、物品的评分偏置、用户评分的偏置、用户和物品之间的兴趣偏好。
|
||
|
||
针对前面三项偏置分数,我在这里举个例子,假如一个电影评分网站全局平均分是3分,《肖申克的救赎》的平均分比全局平均分要高1分。
|
||
|
||
你是一个对电影非常严格的人,你一般打分比平均分都要低0.5,所以前三项从左到右分别就是3,1,-0.5。如果简单的就靠这三项,也可以给计算出一个你会给《肖申克的救赎》打的分数,就是3.5。
|
||
|
||
增加了偏置信息的SVD模型目标函数稍有改变:
|
||
|
||
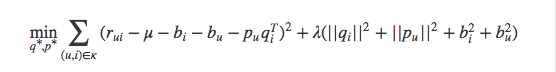
|
||
|
||
和基本的SVD相比,要想学习两个参数:用户偏置和物品偏置。学习的算法还是一样的。
|
||
|
||
### 3 增加历史行为
|
||
|
||
探讨完增加偏执信息的SVD后,接着你再思考一个问题:有的用户评分比较少。事实上这很常见,相比沉默的大多数,主动点评电影或者美食的用户是少数。
|
||
|
||
换句话说,显式反馈比隐式反馈少,那么能不能利用隐式反馈来弥补这一点呢?另外,再考虑多一点,对于用户的个人属性,比如性别等,是不是也可以加入到模型中来弥补冷启动的不足呢?
|
||
|
||
是的,都是可以的,在SVD中结合用户的隐式反馈行为和属性,这套模型叫做SVD++。
|
||
|
||
先说隐式反馈怎么加入,方法是:除了假设评分矩阵中的物品有一个隐因子向量外,用户有过行为的物品集合也都有一个隐因子向量,维度是一样的。把用户操作过的物品隐因子向量加起来,用来表达用户的兴趣偏好。
|
||
|
||
类似的,用户属性,全都转换成0-1型的特征后,对每一个特征也假设都存在一个同样维度的隐因子向量,一个用户的所有属性对应的隐因子向量相加,也代表了他的一些偏好。
|
||
|
||
综合两者,SVD++的目标函数中,只需要把推荐分数预测部分稍作修改,原来的用户向量那部分增加了隐式反馈向量和用户属性向量:
|
||
|
||
$$ \\hat{r}\_{ui} = \\mu + b\_{i} + b\_{u} + \\
|
||
(p\_{u} + |N(u)|^{-0.5}\\sum\_{i\\in{N(u)}}{x\_{i}} + \\sum\_{a\\in{A{u}}}{y\_{a}})q\_{i}^{T} $$
|
||
(滑动查看完整公式)
|
||
|
||
学习算法依然不变,只是要学习的参数多了两个向量:x和y。一个是隐式反馈的物品向量,另一个用户属性的向量。
|
||
|
||
这样一来,在用户没有评分时,也可以用他的隐式反馈和属性做出一定的预测。
|
||
|
||
## 4 考虑时间因素
|
||
|
||
截止到目前,我们还没有正视过一个人性:人是善变的。这个是一个广义的评价,我们在进步也是在变化,今天的我们和十年前的我们很可能不一样了。这是常态,因此,在SVD中考虑时间因素也变得顺理成章。
|
||
|
||
在SVD中考虑时间因素,有几种做法:
|
||
|
||
1. 对评分按照时间加权,让久远的评分更趋近平均值;
|
||
2. 对评分时间划分区间,不同的时间区间内分别学习出隐因子向量,使用时按照区间使用对应的隐因子向量来计算;
|
||
3. 对特殊的期间,如节日、周末等训练对应的隐因子向量。
|
||
|
||
## 总结
|
||
|
||
至此,我们介绍了在Netflix Prize比赛中最为出众的模型:SVD及其一些典型的改进。改进方案分别是:
|
||
|
||
1. 考虑偏置信息;
|
||
2. 考虑隐式反馈和用户属性;
|
||
3. 考虑时间因素。
|
||
其实Netflix Prize比赛上诞生了很多其他优秀的算法,或者把一些已有的算法应用得到很好的效果,比如受限玻尔兹曼机用来融合多个模型,这个我会在后面的专栏文章中专门再讲。
|
||
|
||
好了,最后我要给你留一个思考题,假如矩阵分解面对的数据不是评分数据,而是行为数据,那么今天讲到的损失函数是否依然有效呢?欢迎留言一起讨论。感谢你的收听,我们下次再见。
|
||
|
||

|
||
|