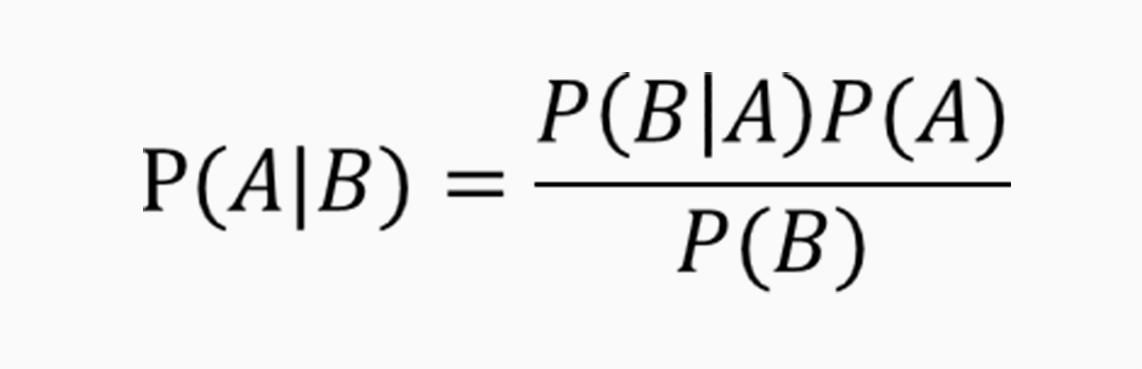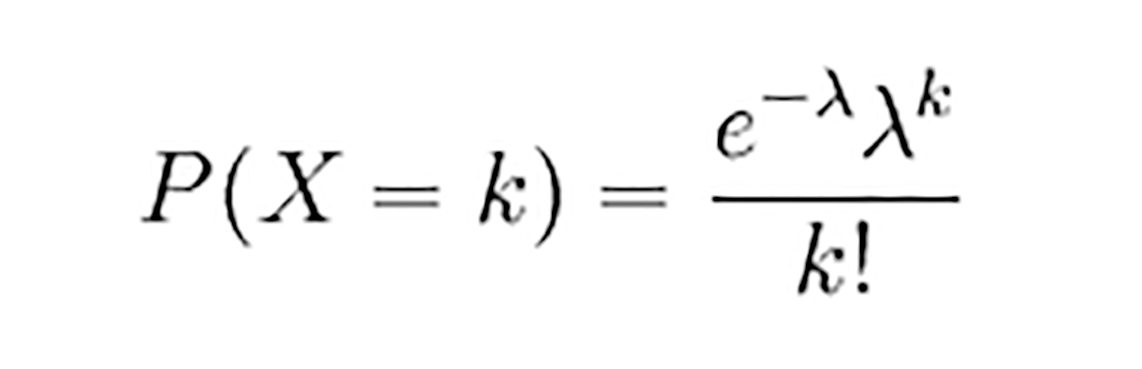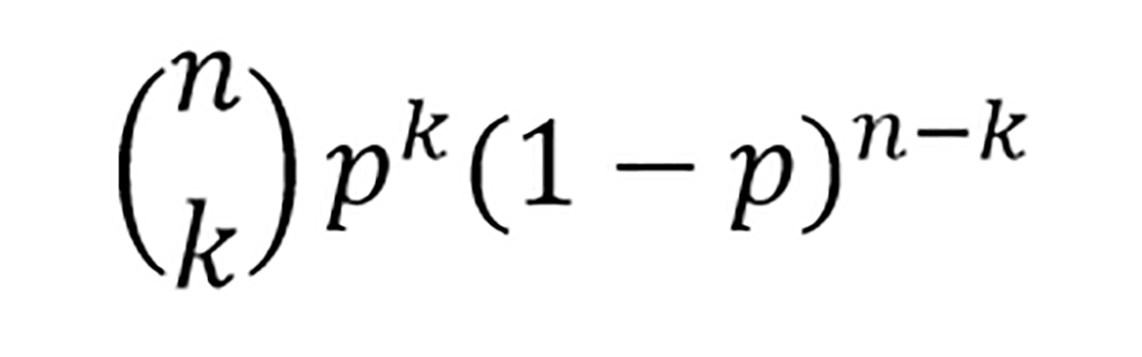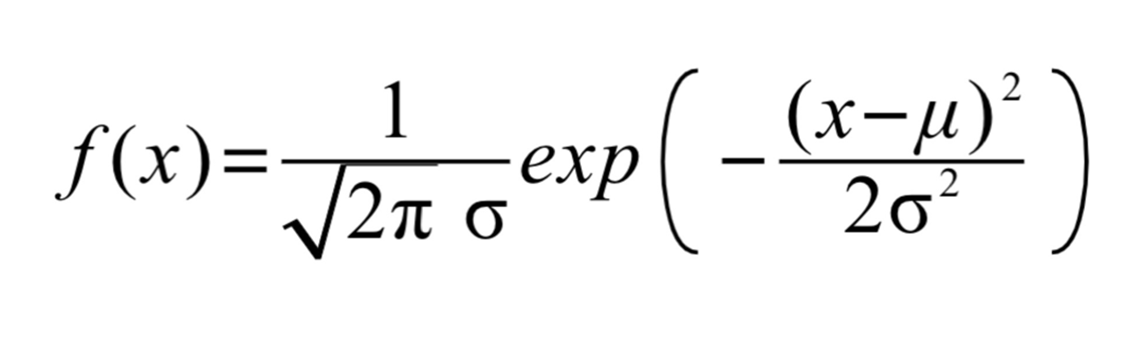12 KiB
05 | 概率统计和排队论:做性能工作必须懂的数理基础
你好,我是庄振运。
上一讲我们讲了和性能优化有关的三大基础定律法则。今天我们继续打基础,讲一点统计方面的数理知识,包括重要的概率统计和排队论。
或许你对概率统计和排队论有点发怵,但这些内容是必须学会的,因为它们很重要。因为它们是性能测试和优化这座高楼大厦的地基。地基打不好,性能测试和优化也不会做得很好。
而且我想强调的是:你完全没有必要惧怕,因为你只需要学习一部分最基础的知识,这些知识对多数人和多数场合大体就够了。还记得上一讲的帕累托法则吗?根据帕累托法则,这一讲的内容或许占不到平时教科书内容的20%,但却可以覆盖80%以上的应用场合。
概率和置信区间
今天的内容我们先从概率和置信区间讲起。
概率(Probability),也称几率和机率,是一个在0到1之间的实数,是对随机事件发生之可能性的度量。这个你应该都懂,不需要我多说。
但概率论中有一个很重要的定理,叫贝叶斯定理,我们做性能测试和分析中经常需要用到,所以我们稍微讲讲。
贝叶斯定理(Bayes’ theorem)描述的是在已知一些条件下,某事件的发生概率。比如,如果已知某癌症与寿命有关,合理运用贝叶斯定理就可以通过得知某人年龄,来更加准确地计算出他患上该癌症的概率。
具体来讲,对两个事件A和B而言,“发生事件A”在“事件B发生”的条件下的概率,与“发生事件B”在“事件A发生”的条件下的概率是不一样的。
然而,这两者的发生概率却是有确定的关系的。就是A事件发生的概率,乘以A事件下B事件发生的概率,这个乘积等于B事件发生概率乘以B事件下A发生的概率。听起来有点拗口,可如果用公式来表示的话其实很简单。
贝叶斯定理的一个用途在于通过已知的任意三个概率函数推出第四个。
另外一个重要的概念是置信区间。置信区间(Confidence interval,CI)是对产生样本的总体参数分布(Parametric Distribution)中的某一个未知参数值,以区间形式给出的估计。相对于后面我们要讲到的点估计指标(比如均值,中位数等),置信区间蕴含了估计精确度的信息。
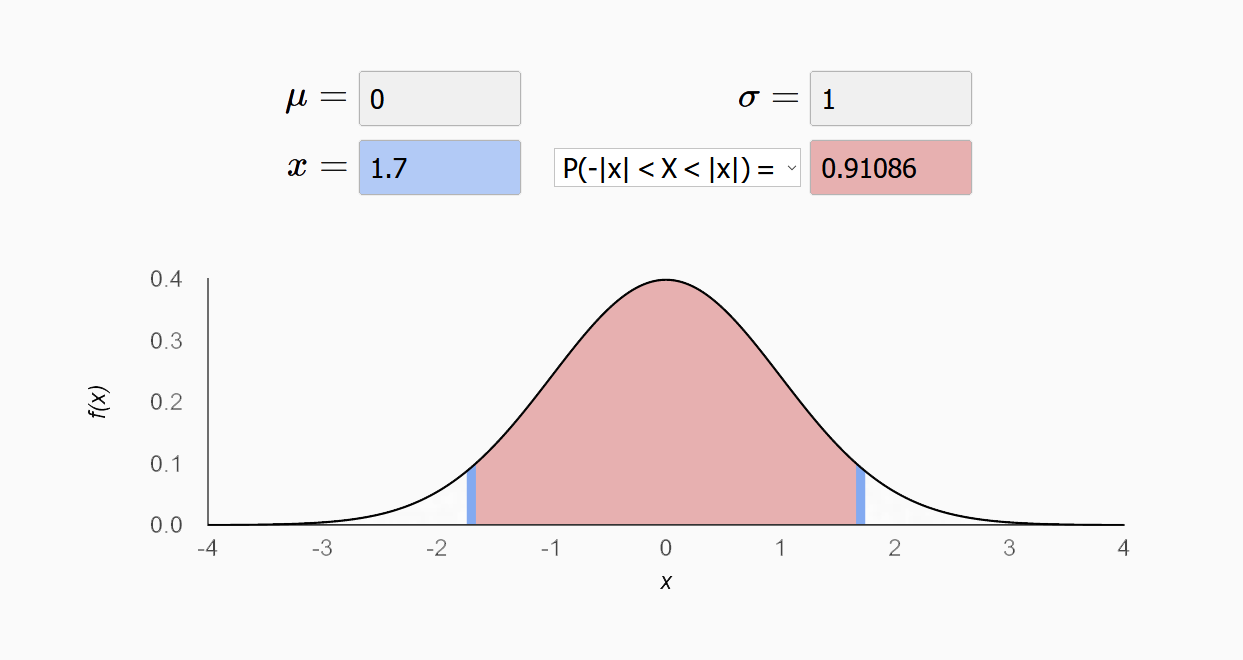
置信区间是对分布(尤其是正态分布)的一种深入研究。通过对样本的计算,得到对某个总体参数的区间估计,展现为总体参数的真实值有多少概率落在所计算的区间里。比如下图是一个标准正态分布的图,阴影部分显示的是置信区间[-1.7,1.7],占了91%的概率。
不难理解,置信水平越高,置信区间就会越宽。一般来说,如果需要涵盖绝大多数的情况,置信区间一般会选择90%或者95%。
了解了概率和置信区间,我们下面去看看如何分析大量数据。
数理统计的点估计指标
做性能测试和优化的过程中会产生大量的数据,比如客户请求的吞吐率,请求的延迟等等。获得这些大量数据后,如何分析和理解这些数据就是一门学问了。通常我们需要处理一下这些数据来求得另外的指标,以方便描述和理解。
描述性统计分析是传统数据分析的基础,这个分析过程可以产生一些描述性指标,比如平均值、中位数、最大值、最小值、百分位数等。
这些描述性指标通常也被称为“点估计”,相对于前面讲到的置信区间,是用一个样本统计量来估计参数值,比较容易理解。这些点估计指标分别有不同的优点和缺点。
平均值:(Mean,或称均值,平均数)是最常用测度值,它的目的是确定一组数据的均衡点。但不足之处是它容易受极端值影响。比如公司的平均收入,如果有一两个员工有特别高的收入,会把大家的平均收入拉高,就是平时我们经常调侃的“被平均”。
需要注意的是,我们有好几种不同的平均值算法。我们平时比较常用的是算术平均值,就是把N个数据相加后的和除以N。但是还有几种其他计算方法,分别适用不同的情况。比如几何平均数,就是把N个数据相乘后的乘积开 N次方。
中位数(Median,又称中值),将数值集合划分为相等的上下两部分,一般是把数据以升序或降序排列后,处于最中间的数。它的优点是不受极端值的影响,但是如果数据呈现一些特殊的分布,比如二向分布,中位数的表达会受很大的负面影响。
四分位数(Quartile)是把所有数值由小到大排列,并分成四等份,处于三个分割点位置的数值就是四分位数。 从小到大分别叫做第一四分位数,第二四分位数等等。四分位数的优点是简单,固定了三个分割点位置。缺点也正是这几个位置太固定,因此不能更普遍地描述其他位置。
百分位数(Percentile)可以看作是四分位数的扩展,是将一组数据从小到大排序,某一百分位所对应数据的值就称为这一百分位的百分位数,以Pk表示第k个百分位数。比如常用的百分位数是P90,P95等等。百分位数不容易受极端值影响,因为有100个位置可以选取,相对四分位数适用范围更广。
几个特殊的百分位数也很有意思,比如P50其实就是中位数,P0其实就是最小值,P100其实就是最大值。
还要注意的是,面对同一组数据,平均值和中位数以及百分位数这些点估计指标,谁大谁小是不一定的,这取决于这组数据的具体离散程度。
比如,我在面试的时候我经常问来面试的人一个问题,就是平均值和P99哪个比较大?答案就是:不确定。
方差/标准差(Variance,Standard Variance),描述的是变量的离散程度,也就是该变量离其期望值的距离。
重要的分布模型
以上的几个描述性的点估计统计指标很简单,但是描述数据的功能很有限。如果需要更加直观并准确的描述,就需要了解分布模型了。
举例来讲,假设我们有一个系统,观察对客户请求的响应时间。如果面对一万个这样的数据,如何对这个数据集合进行描述呢?这时候用分布模型来描述就很合适。
我们简单提一下几个最重要的分布模型,包括泊松分布、二项式分布和正态分布。
泊松分布(Poisson distribution)适合于描述单位时间内随机事件发生的次数的概率分布。如某一服务设施在一定时间内收到的服务请求的次数等。
具体讲,如果随机变量X取0和一切正整数值,在n次独立试验中出现的次数x恰为k次的概率P(X=k)就是:
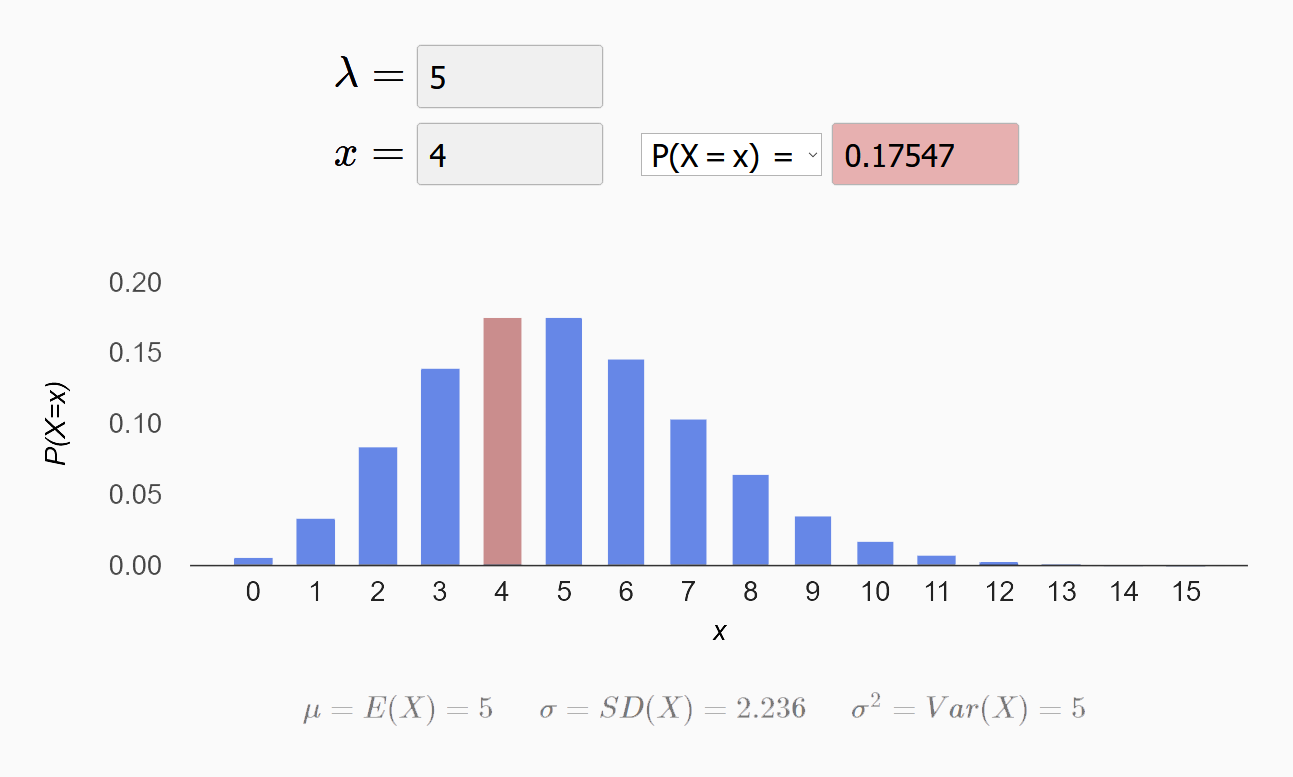
公式中λ是单位时间内随机事件的平均发生次数。像下面这个图,表示的就是λ=5的分布。红色部分是P(X=4)的概率,约为0.17。
当n很大,且在一次试验中出现的概率P很小时,泊松分布近似二项式分布。
二项分布(Binomial distribution),是n个独立的是/非试验中成功的次数的离散概率分布。
这里通常重复n次独立的伯努利试验(Bernoulli trial)。在每次试验中只有两种可能的结果,而且两种结果发生与否互相对立,并且相互独立。也就是说事件发生与否的概率在每一次独立试验中都保持不变,与其它各次试验结果无关。
当试验次数为1时,二项分布服从比较简单的0-1分布。
在n重伯努利试验中,假设一个事件A成功的概率是p, 那么恰好发生 k 次的概率为:
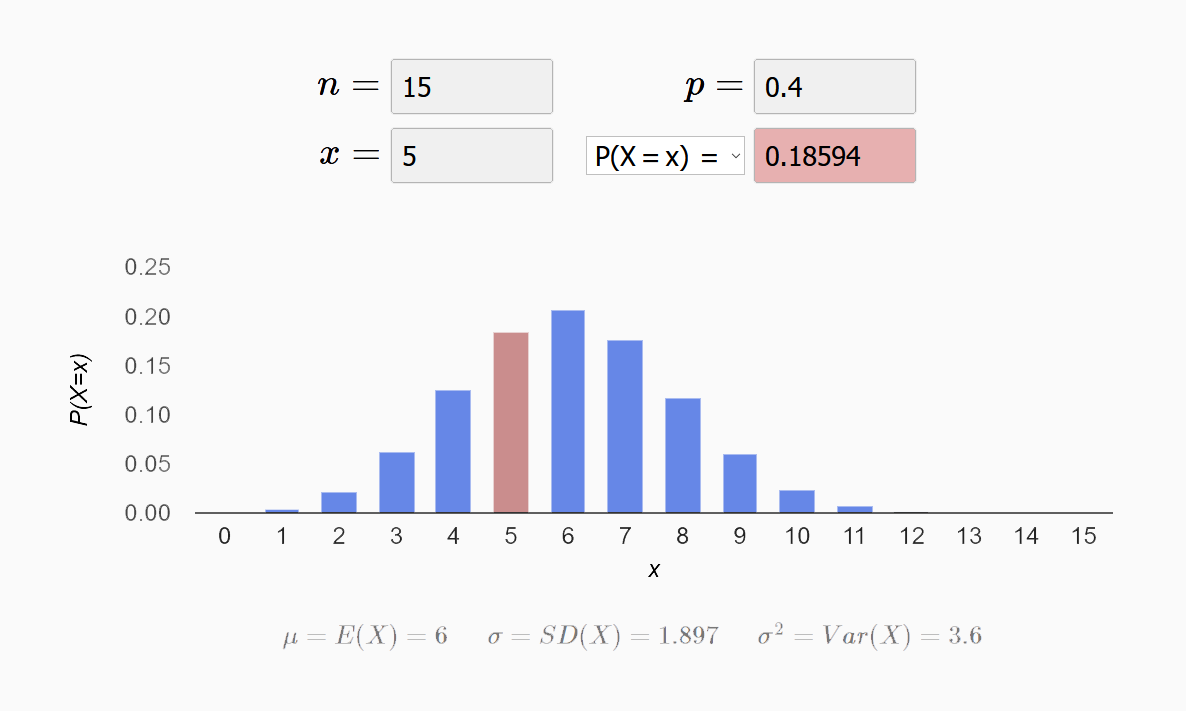
比如下图就是一个二项分布的图,图中红色的是P(X=5)的概率,约为0.18。
正态分布(Normal distribution),也叫高斯分布(Gaussian distribution)。经常用来代表一个不明的随机变量。
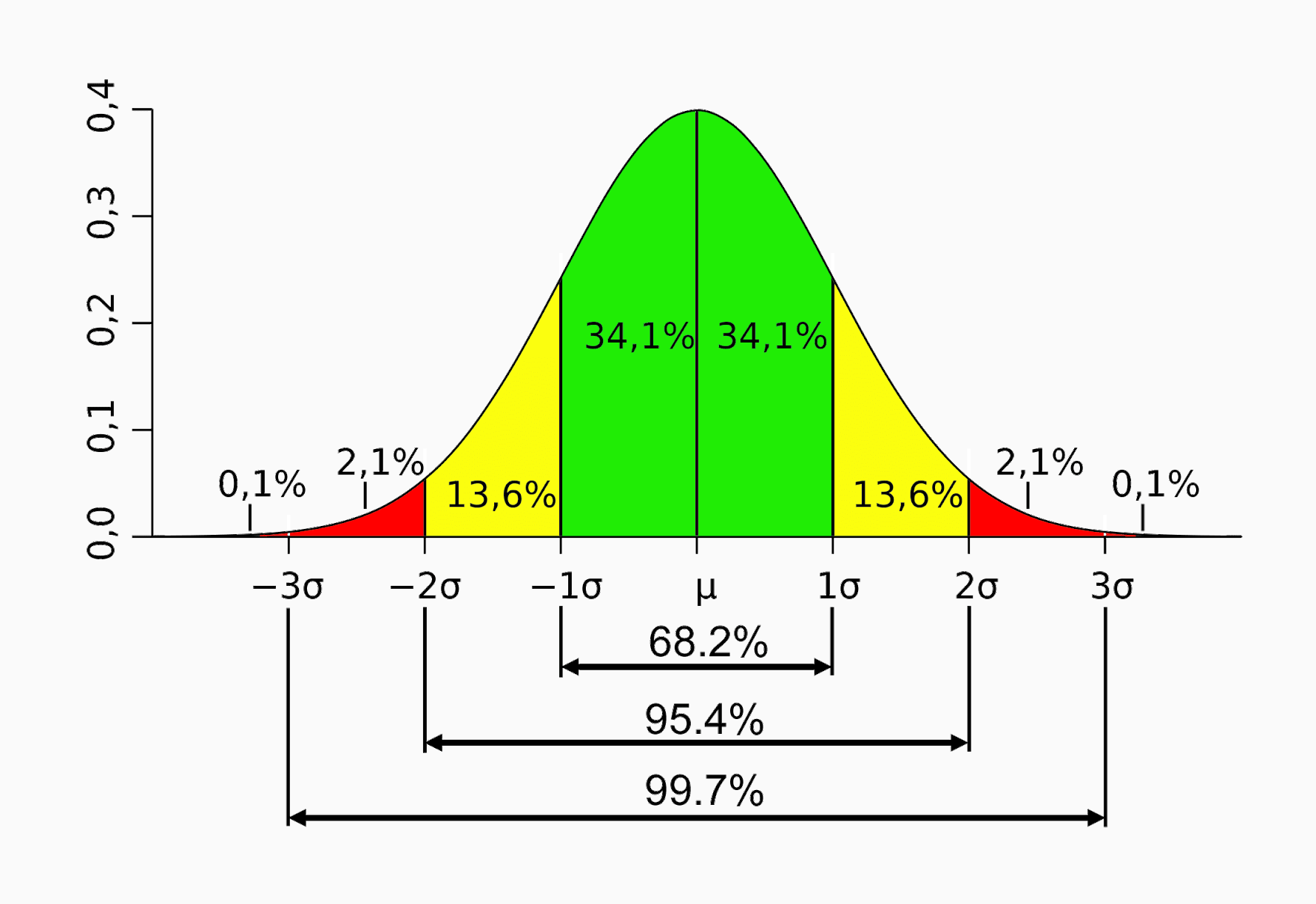
正态分布的曲线呈钟型,两头低,中间高,左右对称,因此经常被称之为钟形曲线。比如下图:
一个正态分布往往记为N(μ,σ^2)。其中的期望值μ决定了其位置,其标准差σ决定了分布的幅度。概率密度函数如下:
当μ = 0,σ = 1时的正态分布是标准正态分布。上图就是一个标准正态分布,线段的值代表了置信区间。比如在期望值附近,左右各一个标准差的范围内,差不多可以囊括68.2%的概率;各两个标准差的范围内,囊括95.4%的概率;各三个标准差的范围内,囊括99.7%的概率。
正态分布的重要性在于,大多数我们碰到的未知数据都呈正态分布状。这意味着我们在不清楚总体分布情况时,可以用正态分布来模拟。
好了,我们这里学习了三个重要分布。如果你看不懂或者记不住这三个分布的公式也没有关系,你只要知道每个分布的大概适应场景就可以了。实际的工作中,很多工具都能帮助我们分析,很少需要我们去具体推导。
排队的理论
上面谈到的三个分布经常被应用到排队理论中,而排队理论在性能工程方面是非常重要的。计算机系统中的很多模块,比如网络数据发送和接收、CPU的调度、存储IO、数据库查询处理等等,都是用队列来缓冲请求的,因此排队理论经常被用来做各种性能的建模分析。
排队论(Queuing Theory),也被称为随机服务系统理论。这个理论能帮助我们正确地设计和有效运行各个服务系统,使之发挥最佳效益。
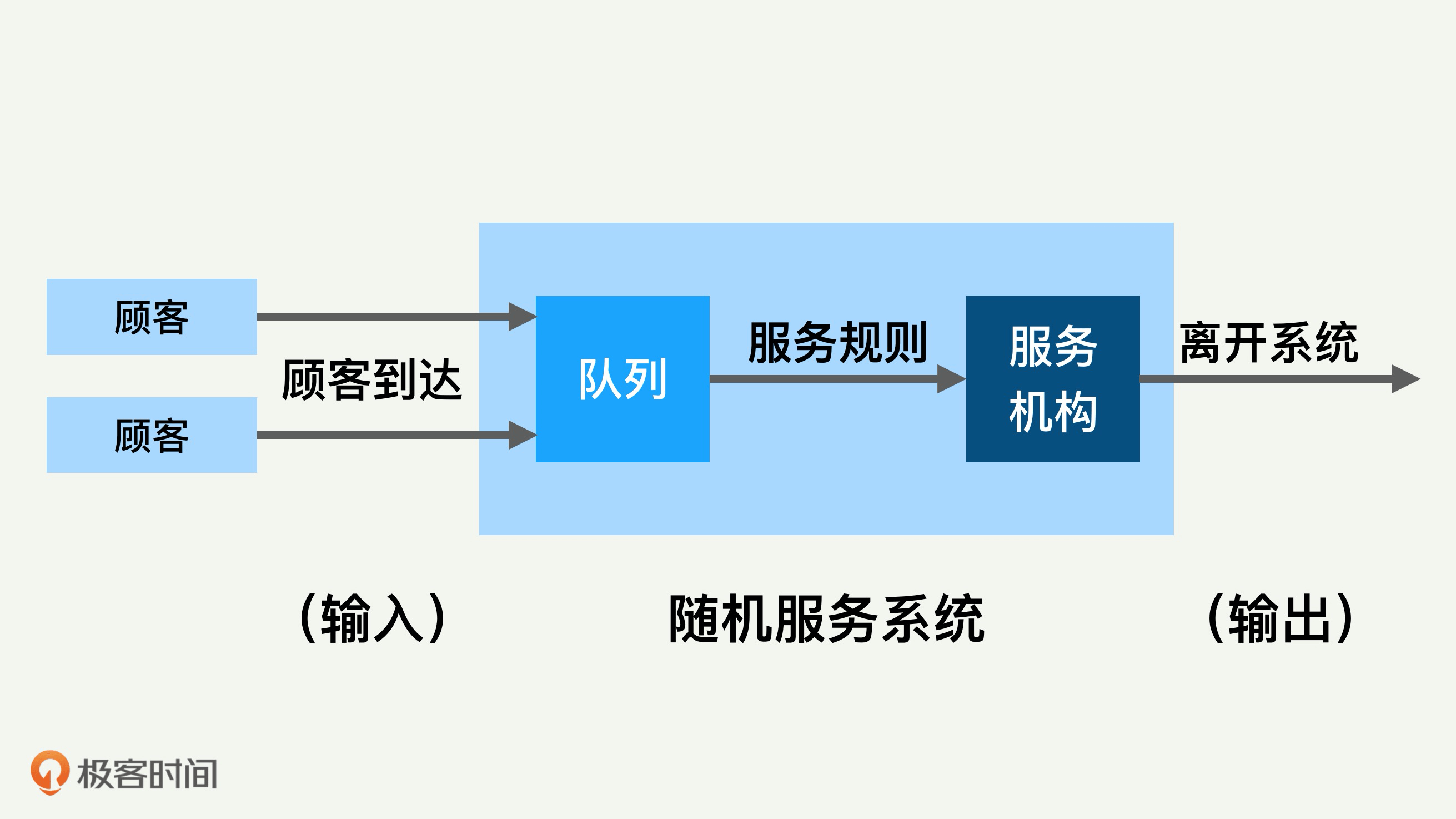
排队论的系统里面有几个重要模块,比如顾客输入过程、队列、排队规则、服务机构等。几个模块之间的关系大体上可以用下面这张图来表示。
主要的输入参数是到达速度、顾客到达分布、排队的规则、服务机构处理速度和处理模型等。
排队系统的输出也有很多的参数,比较重要的是排队长度、等待时间、系统负载水平和空闲率等。所有这些输入、输出参数和我们进行的性能测试和优化都息息相关。
排队的模型有很多,平时我们用得多的有单队列单服务台和多队列多服务台。系统里面各个模块的模型都可以变化,排队论里面还有很多延伸理论。
总结
要想精通任何一门学问和工作,牢固的基础是必须的。对IT工作,包括设计系统、编写程序、系统维护和性能优化而言,牢固的数学基础会使我们的工作如虎添翼。这正如古人赞赏梅花时所说得:“不经一番寒彻骨,怎得梅花扑鼻香“。
我们也常说“根深才能叶茂”,今天讲的内容,包括概率统计和分布模型的知识,都是这样的基础和根基,希望你能牢牢掌握。
思考题
- 你们公司的系统和提供的服务中,有没有性能方面的指标要求?
- 这种指标要求是怎么表述的?比如是平均值,还是某些百分位数?
- 为什么要这样规定指标要求?
欢迎你在留言区分享自己的思考,与我和其他同学一起讨论,也欢迎你把文章分享给自己的朋友。