369 lines
22 KiB
Markdown
369 lines
22 KiB
Markdown
# 03 | 备忘录:如何避免递归中的重复计算?
|
||
|
||
你好,我是卢誉声。
|
||
|
||
从前面的课程中我们已经看到,动态规划问题的一般形式就是求最值。因此我先讲解了什么是最优解问题,在考虑整体最优的情况下,我们需要找到一种办法获取最优解。那么最简单直接的做法是什么呢?
|
||
|
||
其实就是把所有可行的答案**穷举**出来,然后在所有可行的答案中找出满足条件的最值。
|
||
|
||
这样的解法看似“天衣无缝”,但它有着重要的缺陷,而且这个缺陷是我们在面试过程中需要极力避免的:它的执行效率极低。
|
||
|
||
导致这个问题的罪魁祸首是重叠子问题,我已经不止一次提到这个概念了。那么你该**如何解决重叠子问题并提高算法效率呢?**
|
||
|
||
接下来我们就带着这个问题,开始学习今天的内容:备忘录。看看它能否有效解决递归过程中出现的大量重复计算的问题,提高算法效率。
|
||
|
||
## 什么是重叠子问题?
|
||
|
||
斐波那契数列没有求最值的问题,因此严格来说它不是最优解问题,当然也就不是动态规划问题。但它能帮助你理解什么是重叠子问题。首先,它的数学形式即递归表达是这样的:
|
||
|
||
$$F(n)=\\left\\{\\begin{array}{c}
|
||
0,n=0\\\\\\
|
||
1,n=1\\\\\\
|
||
F(n-1)+F(n-2),n>1
|
||
\\end{array}\\right.$$
|
||
|
||
因此写成代码也极为简洁:
|
||
|
||
```
|
||
int Fibonacci(int n) {
|
||
if (0 == n || 1 == n) { return n; }
|
||
if(n > 1) { return Fibonacci(n - 1) + Fibonacci(n - 2); }
|
||
|
||
return 0; // 如果输入n有误,则返回默认值
|
||
}
|
||
|
||
```
|
||
|
||
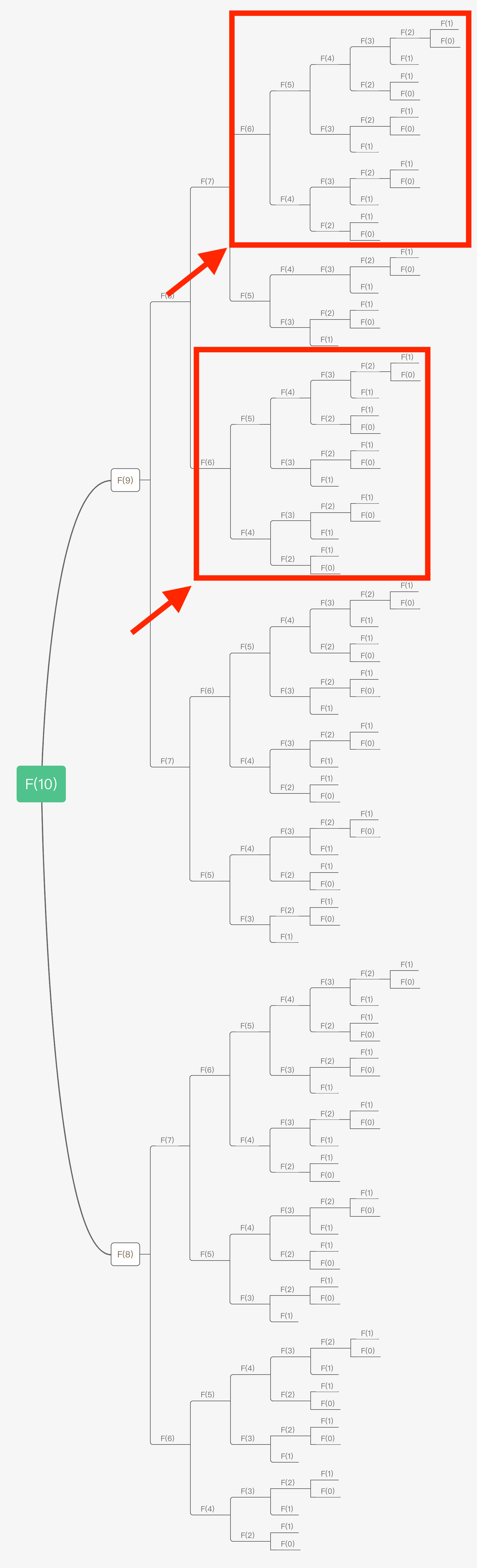
这个代码有问题吗?没问题,但是它效率极低。那么它效率低在哪里呢?假设上面的函数调用输入是10,我把递归树画出来:
|
||
|
||
|
||
|
||
我们要怎么理解这个递归树呢?如果要计算原问题 F(10),你就需要先计算出子问题 F(9) 和 F(8),如果要计算 F(9),你就需要先计算出子问题 F(8) 和 F(7),以此类推。这个递归的终止条件是当 F(1)=1 或 F(0)=0 时结束。
|
||
|
||
我在这里画出整个递归树的目的,在于向你尽可能详细地展示递归的过程,但凡遇到递归问题,你最好都能画出递归树,这对你分析算法的复杂度,寻找算法低效的原因都有巨大帮助。
|
||
|
||
但你也看到了,即便如此简单的递归过程,这个树也十分“巨大”。
|
||
|
||
在画求解树的时候,你可以想出求解过程是怎么进行的,但如果求解树的分支极多,那么很多人就很难继续在脑海中模拟出整个求解过程了。因此问题过于复杂,一般是无法直接画出像上面我画的那棵求解树的,即便递归在数学意义上非常直观。
|
||
|
||
因此,我给你的建议是画出主要的分支路径,帮助你理解和解决面试问题。
|
||
|
||
画完斐波那契数列的求解树之后,你发现问题没有?在我用红色标出的两个区域中,它们的递归计算过程完全相同!
|
||
|
||
这意味着,第2个红色区域的计算是“完全没有必要的”,它是重复的计算。因为我们已经在求解 F(7) 的时候把 F(6) 的所有情况计算过了。因此我们把第2个红色区域的计算称为**重叠子问题**。
|
||
|
||
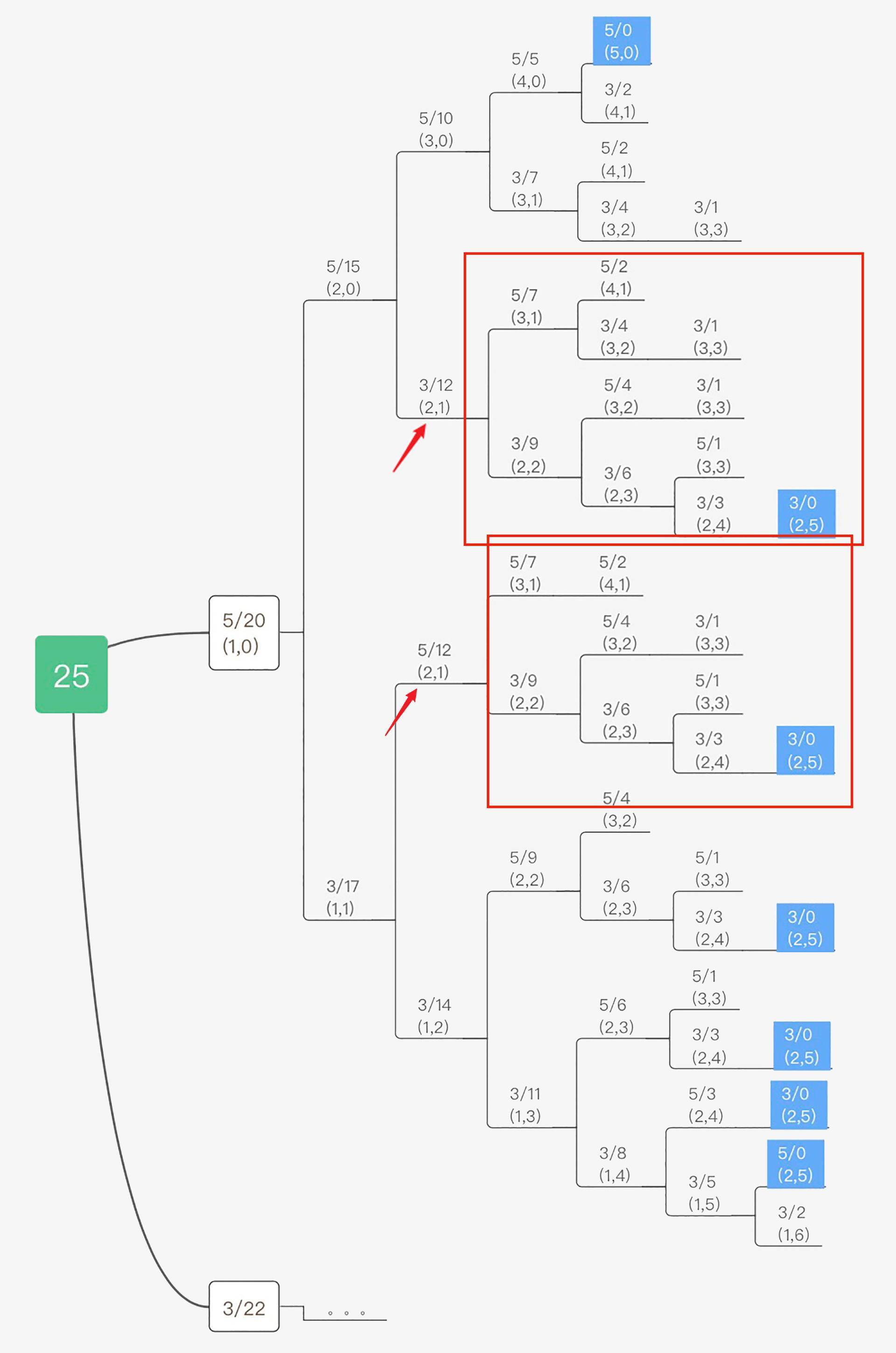
这种问题常见吗?答案是肯定的。让我们回到硬币找零的问题上,我们把上一课的求解树再拿出来观察一下:
|
||
|
||
|
||
|
||
从上图中,我们看到了类似的模式,我同样圈选出了两个红色区域,其中第2个即5/12(2, 1)的递归子问题与第1个 3/12(2, 1) 的递归子问题完全相同,因此它们是**重叠子问题**。
|
||
|
||
对于我们实现的这个递归算法,它的复杂度是多少呢?
|
||
|
||
1. 先考虑子问题的个数(即上图中节点的总数),二叉树节点总数为指数级别,因此子问题个数为指数级 O(2n);
|
||
2. 再考虑求解一个子问题的复杂度:没有计算,因此是 O(1);
|
||
3. 综上所述,该算法的时间复杂度是 O(2n)。
|
||
|
||
事实上在面试或工程实践中,指数级别的复杂度已经很难让人接受了,除非情况特殊,我们必须想办法来优化算法的时间复杂度。
|
||
|
||
该怎么做呢?到这,其实我们要解决的问题已经十分清晰明了了:只需要将重复计算的部分跳过,复用之前已经计算过的结果,以此来加速算法。
|
||
|
||
## 递归中的备忘录:解决重复计算的法宝
|
||
|
||
### 备忘录即正义
|
||
|
||
现在,我们明确了亟待解决的问题:消除重叠子问题,即消灭重复计算的过程。我们可以创建一个**备忘录**(memorization),在每次计算出某个子问题的答案后,将这个临时的中间结果记录到备忘录里,然后再返回。
|
||
|
||
接着,每当遇到一个子问题时,我们不是按照原有的思路开始对子问题进行递归求解,而是先去这个备忘录中查询一下。如果发现之前已经解决过这个子问题了,那么就直接把答案取出来复用,没有必要再递归下去耗时的计算了。
|
||
|
||
对于备忘录,你可以考虑使用以下两种数据结构:
|
||
|
||
1. 数组(Array),通常对于简单的问题来说,使用一维数组就足够了。在后续的课程中,你会看到更为复杂的状态存储过程,届时我会指导你使用更高维度(二维甚至三维)的数组来存储状态。
|
||
2. 哈希表(Hash table),如果你存储的状态不能直接通过索引找到需要的值(比如斐波那契数列问题,你就可以直接通过数组的索引确定其对应子问题的解是否存在,如果存在你就拿出来直接使用),比如你使用了更高级的数据结构而非简单的数字索引,那么你还可以考虑使用哈希表,即字典来存储中间状态,来避免重复计算的问题。
|
||
|
||
我们先来看看如何使用备忘录来解决斐波那契数列问题,直接上代码。
|
||
|
||
Java 实现:
|
||
|
||
```
|
||
int fibonacci(int n, int[] memo) {
|
||
if (0 == n || 1 == n) { return n; }
|
||
if (memo[n] != 0) { return memo[n]; } // 看来备忘录中找到了之前计算的结果,既然找到了,直接返回,避免重复计算
|
||
|
||
if(n > 1) {
|
||
memo[n] = fibonacci(n - 1, memo) + fibonacci(n - 2, memo);
|
||
return memo[n];
|
||
}
|
||
|
||
return 0; // 如果数值无效(比如 < 0),则返回0
|
||
}
|
||
|
||
int fibonacciAdvance(int n) {
|
||
int[] memo = new int[n + 1];
|
||
return fibonacci(n, memo);
|
||
}
|
||
|
||
```
|
||
|
||
C++ 实现:
|
||
|
||
```
|
||
int Fibonacci(int n, std::vector<int>& memo) {
|
||
if (0 == n || 1 == n) { return n; }
|
||
if (memo[n] != 0) { return memo[n]; } // 看来备忘录中找到了之前计算的结果,既然找到了,直接返回,避免重复计算
|
||
|
||
if(n > 1) {
|
||
memo[n] = Fibonacci(n - 1, memo) + Fibonacci(n - 2, memo);
|
||
return memo[n];
|
||
}
|
||
|
||
return 0; // 如果数值无效(比如 < 0),则返回0
|
||
}
|
||
|
||
int FibonacciAdvance(int n) {
|
||
std::vector<int> memo(n + 1, 0); // 初始化备忘录,在这里我使用数组
|
||
return Fibonacci(n, memo);
|
||
}
|
||
|
||
```
|
||
|
||
从以上代码可以看出,我在第12行创建了一个基于数组的备忘录,用来存储中间计算状态。第3行代码十分关键,它从我们的备忘录中查询对应索引位置存储的状态是否已经计算过(值 > 0时),如果计算过了,那么就直接返回之前计算过的答案。
|
||
|
||
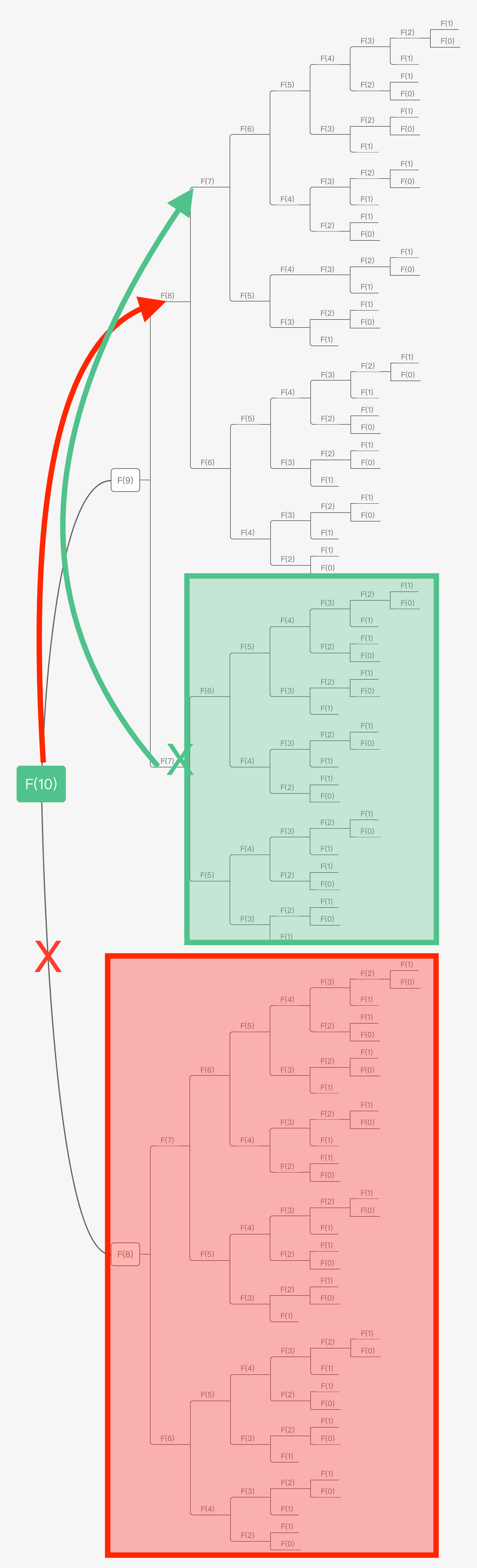
我在下图中,把两个重复计算的分支画了出来,你可以清晰地看到,这些被圈出的子问题,是完全没有必要进行再次计算的,我们可以直接拿之前的计算结果来使用。
|
||
|
||
|
||
|
||
实际上,这就是我们所熟知的“剪枝与优化”,在这里我把一棵存在巨量冗余的递归树通过剪枝,改造成了一幅不存在冗余的递归图,极大减少了子问题(即递归图中节点)的个数。
|
||
|
||
通过这种方式,我们大幅缩减了算法的计算量,所有重复的部分都被跳过了。这时,我们再看看递归的复杂度是多少?
|
||
|
||
1. 同样,我们先考虑子问题的个数(即上图中节点的总数)。由于本算法不存在冗余计算,子问题就是 F(1), F(2), F(3) ... F(10),因此为 O(n);
|
||
2. 再考虑求解一个子问题的复杂度:没有计算,因此是 O(1);
|
||
3. 综上所述,该算法的时间复杂度是O(n)。
|
||
|
||
使用算法解决重复计算的第一步就是需要将问题定义成函数,比如上面的硬币问题,我们可以将满足x的最小硬币总数定义成一个函数f(x):
|
||
|
||
$$F(x)=\\left\\{\\begin{array}{c}
|
||
min(f(x-c)+1), x>0,f(x-c)\\ne-1,c\\in C\\\\\\
|
||
0,x=0\\\\\\
|
||
\-1,x<0
|
||
\\end{array}\\right.$$
|
||
|
||
说明:在这个函数中,C 指的是硬币面值的集合。
|
||
|
||
那如果要处理这个问题,我们只需要避免每次都重复计算 F(x) 的结果就行了。如果有一次的路径中已经计算了 F(8),那么如果在其它的路径中再次遇到 F(8) 的时候,我们就不需要再次计算这个路径了。
|
||
|
||
所以我们需要一个集合来存储所有F(x)的结果,F(x) 在计算时首先查询集合中是否存储了 F(x) 的结果,如果有则返回,没有再执行整个计算步骤。
|
||
|
||
看来,我们已经把指数级 O(2n) 时间复杂度的问题进行了“疯狂”的简化。相较于暴力递归,这就是传说中的“降维打击”。
|
||
|
||
### 使用备忘录求解硬币找零问题
|
||
|
||
现在,让我们再次回到硬币找零问题去实践一遍。首先这是一个可以使用动态规划解决的问题,它存在最优化问题;其次,就像我刚才所说的,该问题存在重叠子问题。
|
||
|
||
现在,让我们来看看如何使用备忘录,对硬币找零算法的复杂度进行“大刀阔斧”的简化。
|
||
|
||
我们仿照使用备忘录提高斐波那契数列算法效率的方法,对硬币找零算法进行剪枝和优化。为了简单起见,我在这里直接贴出改进后的算法实现。
|
||
|
||
Java 实现:
|
||
|
||
```
|
||
int getMinCountsHelper(int total, int[] values, int[] memo) {
|
||
int savedMinCount = memo[total];
|
||
if (savedMinCount != -2) { return savedMinCount; }
|
||
|
||
|
||
int valueLength = values.length;
|
||
int minCount = Integer.MAX_VALUE;
|
||
for (int i = 0; i < valueLength; i ++) { // 遍历所有面值
|
||
int currentValue = values[i];
|
||
// 如果当前面值大于硬币总额,那么跳过
|
||
if (currentValue > total) { continue; }
|
||
|
||
// 使用当前面值,得到剩余硬币总额
|
||
int rest = total - currentValue;
|
||
int restCount = getMinCountsHelper(rest, values, memo);
|
||
// 如果返回-1,说明组合不可信,跳过
|
||
if (restCount == -1) { continue; }
|
||
|
||
// 保留最小总额
|
||
int totalCount = 1 + restCount;
|
||
if (totalCount < minCount) { minCount = totalCount; }
|
||
}
|
||
|
||
// 如果没有可用组合,返回-1
|
||
if (minCount == Integer.MAX_VALUE) {
|
||
memo[total] = -1;
|
||
return -1;
|
||
}
|
||
|
||
memo[total] = minCount; // 记录到备忘录
|
||
return minCount; // 返回最小硬币数量
|
||
}
|
||
|
||
int getMinCountsSol() { // 入口函数
|
||
int[] values = { 3, 5 }; // 硬币面值
|
||
int total = 14; // 总值
|
||
|
||
int[] memo = new int[total + 1];// , -2); // 备忘录,没有缓存的元素为-2
|
||
Arrays.fill(memo, -2);
|
||
memo[0] = 0; // 其中0对应的结果也是0,首先存在备忘录中
|
||
|
||
// 求得最小的硬币数量,并输出结果
|
||
return getMinCountsHelper(total, values, memo); // 输出结果
|
||
}
|
||
|
||
```
|
||
|
||
C++ 实现:
|
||
|
||
```
|
||
int GetMinCountsHelper(int total, const std::vector<int>& values, std::vector<int>& memo) {
|
||
auto savedMinCount = memo[total];
|
||
if (savedMinCount != -2) { return savedMinCount; }
|
||
|
||
int valueLength = values.size();
|
||
int minCount = INT_MAX;
|
||
for (int i = 0; i < valueLength; i ++) { // 遍历所有面值
|
||
int currentValue = values[i];
|
||
// 如果当前面值大于硬币总额,那么跳过
|
||
if (currentValue > total) { continue; }
|
||
|
||
// 使用当前面值,得到剩余硬币总额
|
||
int rest = total - currentValue;
|
||
int restCount = GetMinCountsHelper(rest, values, memo);
|
||
// 如果返回-1,说明组合不可信,跳过
|
||
if (restCount == -1) { continue; }
|
||
|
||
// 保留最小总额
|
||
int totalCount = 1 + restCount;
|
||
if (totalCount < minCount) { minCount = totalCount; }
|
||
}
|
||
|
||
// 如果没有可用组合,返回-1
|
||
if (minCount == INT_MAX) {
|
||
memo[total] = -1;
|
||
return -1;
|
||
}
|
||
|
||
memo[total] = minCount; // 记录到备忘录
|
||
return minCount; // 返回最小硬币数量
|
||
}
|
||
|
||
int GetMinCountsSol() { // 入口函数
|
||
std::vector<int> values = { 3, 5 }; // 硬币面值
|
||
int total = 11; // 总值
|
||
|
||
std::vector<int> memo(total + 1, -2); // 备忘录,没有缓存的元素为-2
|
||
memo[0] = 0; // 其中0对应的结果也是0,首先存在备忘录中
|
||
|
||
// 求得最小的硬币数量,并输出结果
|
||
return GetMinCountsHelper(total, values, memo); // 输出答案
|
||
}
|
||
|
||
```
|
||
|
||
相较于我在上一课实现的代码,我在函数中加入了一个memo参数。
|
||
|
||
因此,对于原来实现的代码,算法时间复杂度可以概括为:
|
||
|
||
1. 先考虑子问题的个数,我只画了这颗树的一部分,因此从树上这个比较难看出来,但从斐波那契数列的题目上我们可以推广,得到其个数是 O(nm), m=|values|,即指数级别;
|
||
2. 再考虑求解一个子问题的复杂度:每个子问题中含有一个循环,因此时间复杂度为 O(m), m=|values|;
|
||
3. 综上所述,该算法的时间复杂度是 O(mnm), m=|values|。
|
||
|
||
而通过备忘录优化后的算法时间复杂度为:
|
||
|
||
1. 先考虑子问题的个数,如果我们求n元总额的硬币最小数量,那么子问题最多就是 0…n 个,一共 n+1 个子问题;
|
||
2. 因为我们缓存了子问题的数量,所以其实每个子问题都只会被求解一次;
|
||
3. 针对每个子问题求解,我们都需要通过硬币面额数量知道需要筛选的子问题数量,每个子问题求解时的时间是 O(m), m=|values|;
|
||
4. 最后我们可以得知,采用备忘录形式时,整个时间复杂度就是子问题的数量乘以需要考虑的面额数量,也就是 O(m\*n), m=|values|。
|
||
|
||
我在这里创建的备忘录memo其实是一个缓存数组,每次求解函数F(x)之后都会将结果缓存在数组中。数组初始化长度是total+1,也就是可以存储0-total的计算结果。所有元素的初值都是-2,表示没有缓存。然后我们将memo\[0\] 设置为0,表示公式中如果x为0,那么F(x)的结果也就是0。
|
||
|
||
接着在 GetMinCountsHelper 函数中,先查找memo中是否已经缓存了当前total的值。如果有则直接返回,如果没有那么重新计算。
|
||
|
||
重新计算完成后,如果结果为-1(即无效组合),那么就将当前total对应的缓存设置为-1,否则设置为我们计算的结果。
|
||
|
||
通过备忘录,我们避免了重复计算,即避免重复计算那些已经计算过的子问题。
|
||
|
||
## 重叠子问题处理模式
|
||
|
||
现在,你已经知道了如何处理具体的问题:比如斐波那契数列和硬币找零问题。但是如果我们遇到了类似新问题该如何处理呢?这里我总结一下对这类问题的处理方法。
|
||
|
||
假设面试问题是这样的:当目标为 x,其中x可能是一个任意长度的向量,目标可能包含多个元素,求最优解 F(x)。举个例子,比如在硬币这个问题里,x 就是硬币总额度,F(x)就是最少的硬币数量。
|
||
|
||
同时,我们还需要知道问题是求最小值还是最大值,并以此来定义我们的数值函数 G(t)。如果求最小值,那么 G 是 min,如果求最大值,那么 G 就是 max。
|
||
|
||
除此之外,我们还需要通过当前的问题获得后续的一系列子问题,假定当前得到子问题的参数为 c,得到后续子问题的函数是 S,那么这个函数就是 S(x, c)。
|
||
|
||
接着,我们就可以用 F(S(x, c)) 来求得子问题的结果。
|
||
|
||
我们再定义一个函数 V(x),该函数可以聚合当前参数c和当前子问题的结果。最后,我们还要定义每一步如何与子问题进行叠加。定义一个叠加函数 H(x)。
|
||
|
||
综上所述,最后得到如下求解公式:
|
||
|
||
$$F(x) = H(G(V(F(S(x, c)), c)))$$
|
||
|
||
因此,当你解决类似问题时,只需要把问题套用到上面的公式(框架)中,就能用一个递归函数来描述所有的问题。你可以尝试把斐波那契数列和硬币问题分别套入这个模型,就知道后面的问题定义该怎么举一反三了。
|
||
|
||
在定义好问题后,你就可以编写基于递归算法的代码了。不过需要注意,上面的公式并不包含边界值的处理。所谓的边界值就是无法再分解为子问题的子问题。
|
||
|
||
比如在硬币找零问题中,x 为0的时候就是一个所谓的边界值。只要处理好递归函数和边界值,我们就能一通百通了。
|
||
|
||
## 重叠子问题缓存的限制
|
||
|
||
我们刚刚学习了重叠子问题的处理模式,提炼出了一个通用的求解公式。你可能会问,这种利用重叠子问题的缓存来提升速度的方法是不是万灵药呢?
|
||
|
||
有一句老话,叫计算机中不存在“银弹”,也就是说没有任何一种方法能够解决世界上的所有问题。通过备忘录的思想来处理重叠子问题的方法亦是如此。
|
||
|
||
1. 我们回想一下在上一课中提到过的问题,就有不少是不存在重叠子问题的,比如八皇后问题。既然没有重叠子问题,那么通过备忘录来对其优化加速,又从何谈起呢?
|
||
|
||
2. 有些问题虽然看起来像包含“重叠子问题”的子问题,但是这类子问题可能具有后效性,但我们追求的是**无后效性**。所谓无后效性,指的是在通过A阶段的子问题推导B阶段的子问题的时候,我们不需要回过头去再根据B阶段的子问题重新推导A阶段的子问题,即子问题之间的依赖是单向性的。
|
||
|
||
|
||
所以说,如果一个问题可以通过重叠子问题缓存进行优化,那么它肯定都能被画成一棵树。希望你能牢记这些限制,不然可能抓破头皮都没法解决问题,最后陷入死胡同。
|
||
|
||
## 方案弊端
|
||
|
||
我们可以看到,通过重叠子问题缓存可以极大加速我们的代码执行效率。但是凡事都有两面性,我们毋庸置疑,这种方案肯定是通过某种牺牲换取了性能的提升。
|
||
|
||
在硬币找零问题中,我们在代码里加入了一个memo数组作为备忘录,这个数组的大小是钱币总额+1。如果计算出F(x)的结果,就把F(x)的结果存在数组中x的位置,这样后续再计算相同的子问题时,我们就可以利用缓存来避免重复计算了。
|
||
|
||
但这样有个问题,如果我们的钱币总额数量非常巨大,那这个数组的大小就会非常巨大,导致的结果就是会占据大量的内存存储空间,而且有很多的数字其实是不会被求解的,存在很多的“存储空洞”。显然,这是一种浪费。
|
||
|
||
同样,如果考虑为了节省空间,那么我们可以使用哈希表,但是哈希表的检索性能肯定不如数组。你可能会说,哈希表的插入和查找的算法复杂度是 O(1) 啊,它怎么可能会慢呢?
|
||
|
||
原因在于,哈希表通常都会使用经过设计的数据结构(比如拉链法)来避免记录碰撞,因此实际的速度肯定不如直接访问数组的特定位置。
|
||
|
||
因此在这个问题里,我们仍然优先选用数组和指定的索引来快速访问数据。
|
||
|
||
话说回来,如果遇到一个目标结果 x 是一个向量的情况下,这个数组就会随着向量维度一起提升,比如如果 x 是二维向量,那么缓存数组就必须是二维数组,以此类推。因此向量维度提升造成的空间压力也可能是巨大的。
|
||
|
||
所以在面试中,你需要根据实际情况,在空间和时间中寻求一个平衡,虽然这样的经验需要积累,但更多的时候是需要你在编写代码前,将这个问题考虑在内。
|
||
|
||
## 课程总结
|
||
|
||
今天我们学习了重叠子问题这一概念,通过斐波那契数列展现了重复计算引发的问题:暴力的递归性能低下。并在此基础上提出了备忘录的思想。
|
||
|
||
备忘录的思想极为重要,特别是当求解的问题包含**重叠子问题**时,只要面试的问题包含重复计算,你就应该考虑使用备忘录来对算法时间复杂度进行简化。具体来说,备忘录解法可以归纳为:
|
||
|
||
1. 用数组或哈希表来缓存已解的子问题答案,并使用自顶向下的递归顺序递归数据;
|
||
2. 基于递归实现,与暴力递归的区别在于备忘录为每个求解过的子问题建立了备忘录(缓存);
|
||
3. 为每个子问题的初始记录存入一个特殊的值,表示该子问题尚未求解(如无此记录,或像求解斐波那契数列题目中那样初始化成0);
|
||
4. 在求解过程中,从备忘录中查询。如果未找到或是特殊值,表示未求解;否则取出该子问题的答案,直接返回。
|
||
|
||
与此同时,在求解最优解问题的时候,画出基本的递归树结构,能极大地降低问题的难度。因此,我建议你在解决此类问题的时候尝试使用这个方法。
|
||
|
||
含有备忘录的递归算法已经与动态规划思想十分相似了,从效率上说也是如此。没错!我们又进了一步。备忘录让我们实现了对算法时间复杂度的“降维打击”,这与贪心算法到递归的进步程度不同,这是真正意义上的动态规划思维:
|
||
|
||
1. 我们考虑了整体最优;
|
||
2. 在计算的过程中保存计算当中的状态,并在后续的计算中复用之前保存的状态。
|
||
|
||
记住使用备忘录来优化你的算法时间复杂度,它是提高算法效率的高级手段。我们距真正的动态规划咫尺之遥,除了重叠子问题,你还需要了解什么是**最优子结构**和**状态转移方程**,我会从下节课开始讲起。
|
||
|
||
## 课后思考
|
||
|
||
到目前为止,我在课程中展示算法的代码实现时,使用的递归方式都是自上而下的,那么请你思考一下这个问题:递归的顺序有办法倒转过来吗(变成自底向上)?如果可以,应该怎么做?如果不能,为什么?
|
||
|
||
欢迎留言和我分享你的答案,我会第一时间给你反馈。如果今天的内容对你有所启发,也欢迎把它分享给你身边的朋友,邀请他一起学习!
|
||
|