18 KiB
31|跳表:Redis是如何存储有序集合的?
你好,我是微扰君。
上一讲我们一起学习了布隆过滤器,它可以帮助我们用更低的存储成本、更高效地判断某个元素是否在一个集合中出现,当然代价是一定的误判率。总的来说,布隆过滤器特别适合用来解决Redis中缓存穿透的问题。
今天,我们同样来讨论一个在Redis中发挥巨大作用的数据结构:跳表。如果你有一定的Redis使用经验,常用的ZSET底层实现就是基于跳表的。
跳表这个数据结构,其实在之前介绍红黑树的时候我们简单提到过,和红黑树一样,它可以非常高效地维护有序键值对,插入、查询和删除的平均时间复杂度都是O(logN),所以被Redis用来存储有序集合。但在时空复杂度差不多的情况下,跳表比红黑树实现起来要简洁优雅得多。
我个人认为,跳表几乎在每个方面都比红黑树更好,当然红黑树由于发明更早,得到了更广泛的应用,所以很多TreeMap之类的语言原生的数据结构还是常常采用红黑树。但是跳表作为一种非常高效的有序集合的实现,背后的原理很值得我们学习。
那跳表是如何设计、实现的呢,我们开始今天的学习之旅。
跳表为什么诞生
故事的开头,还是要从链表说起。
之前讲红黑树(点这里复习)我们也提到,如果要实现一个字典这样的数据结构,其实可以直接用一个线性数据结构,来存储所有的元素,至于每次插入元素前如何判断元素是否存在,也很简单,遍历一遍就可以了。
但是这样的时间复杂度不是特别好,一种优化思路就是尽量让这个线性的数据结构有序,方便快速二分查找,更高效,因此我们也就延伸出了基于树状结构的二叉搜索树,以及对平衡性进一步优化的平衡二叉搜索树。
除此之外,是否还有其他高效的、可以加快搜索速度的优化方式呢?
可能你会想到哈希表,当然了哈希表也是一个思路,事实上,在Redis对有序集合的实现里,我们同时维护了跳表和哈希表,为的就是利用单值查询时哈希表的高效性,但哈希表的存储是无序的,这意味着当我们想要使用范围查询的时候,相比于红黑树或者跳表这样有序的数据结构,哈希表就会产生一定的劣势(点这里复习)。
其实,不采用树状结构,仍然采用链表,再通过一些数据结构上的调整,我们也是可以实现类似二分查询这样跳跃查询效果的。这就是跳表主要被发明出来的动机。
跳表具体解决什么问题
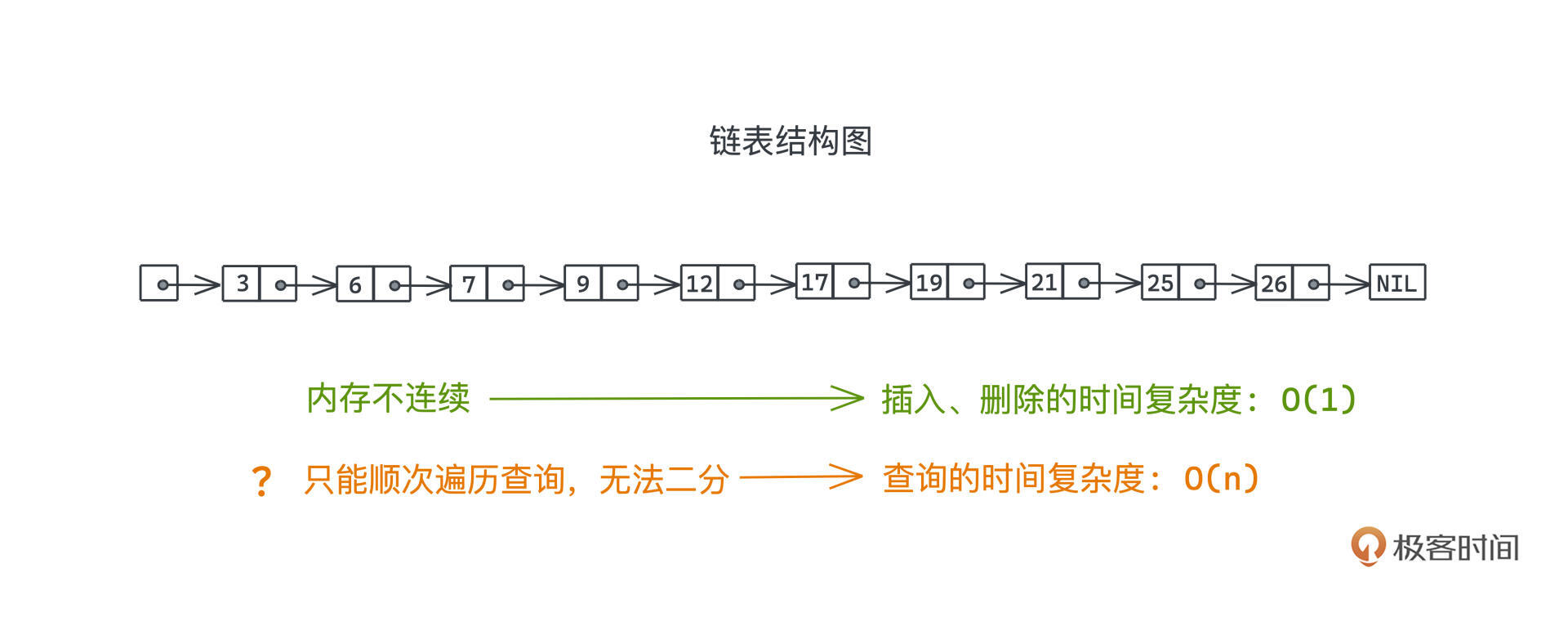
先来仔细回顾一下如果用链表存储有序集合,在查询的时候会碰到什么样的问题?看这张典型的链表结构图(出自跳表原始的论文):
这里我们讨论的是有序集合,所以会让整个链表是有序排列的。
要存储有序集合,链表相比数组这样容器的好处,我们之前已经仔细讨论过了(点这里复习),主要就是在插入的时候,由于链表本身不要求内存连续,所以插入和删除的时间复杂度是O(1),而数组为了保持内存空间的连续性,需要花费O(n)的成本做插入和删除的操作。
但同样的,也正是因为链表内存不连续,我们在基于key查询链表节点时,即使整个链表已经是按照key有序排列了,我们仍然需要顺次遍历进行查询,不能像在有序数组中那样二分地跳跃查询。O(n)的查询复杂度,显然没有有效地利用有序集合的有序特性。因此在这一点上,红黑树完胜。
那链表真的没有办法得到接近二分查找的时间复杂度了吗?只通过链表本身肯定是不行了,我们找到的本质问题是:链表不依次遍历就没有办法寻址到每一个节点,但是如果我们有办法在链表上增加一些捷径,跳着走呢?
链表是怎么设计的
这个想法有点抽象,我们找生活中的场景来类比联想。
请你回想自己每次从一个城市去往另一个城市,是怎么换乘公共交通的?是不是先到本地的机场或者火车站,乘坐站距比较大、速度比较快的飞机或者火车,再换成市内的、站距小的交通工具比如公交车、地铁。
这样的换乘选择就是考虑到,直接坐地铁的耗时,比先坐火车再换地铁长得多,因为地铁站比较密集,速度也比较慢,而高铁则快得多,一站相当于地铁的很多站。
那回到链表上,我们把一个个遍历链表节点比作是一站站地铁,如果在链表上能加一些间距更大的火车站,自然就快得多。
这就是跳表的思想本质,具体来说就像图里这样:
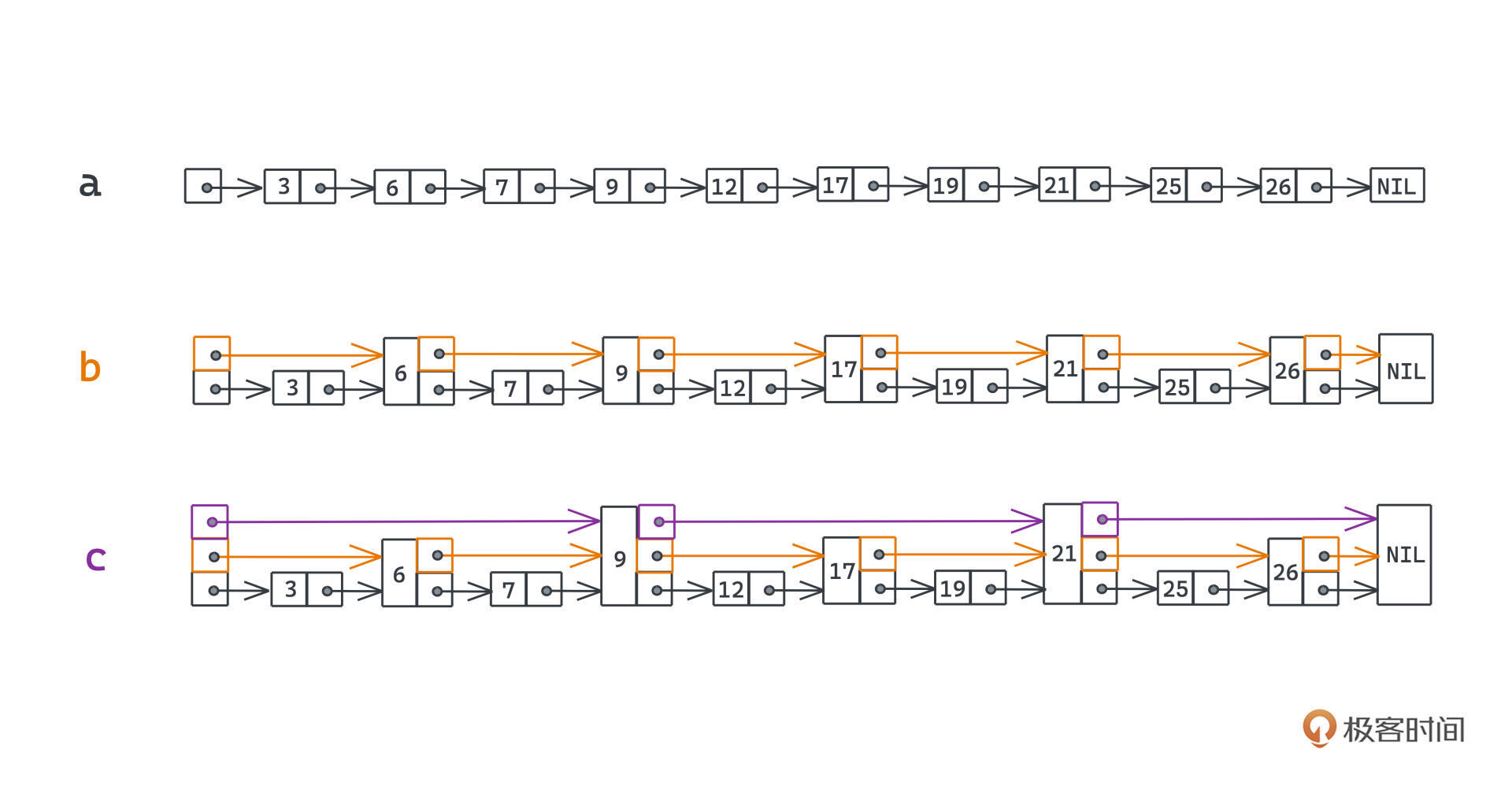
我们会给链表上增加一些额外的层和指针,越高的层,指针指向的下一个节点会跳跃更大的距离,越低的层,指针间距越小;所有的节点都会出现在最低层,也就是第一层,这一层就是一个包含了所有有序集合中元素的有序链表。
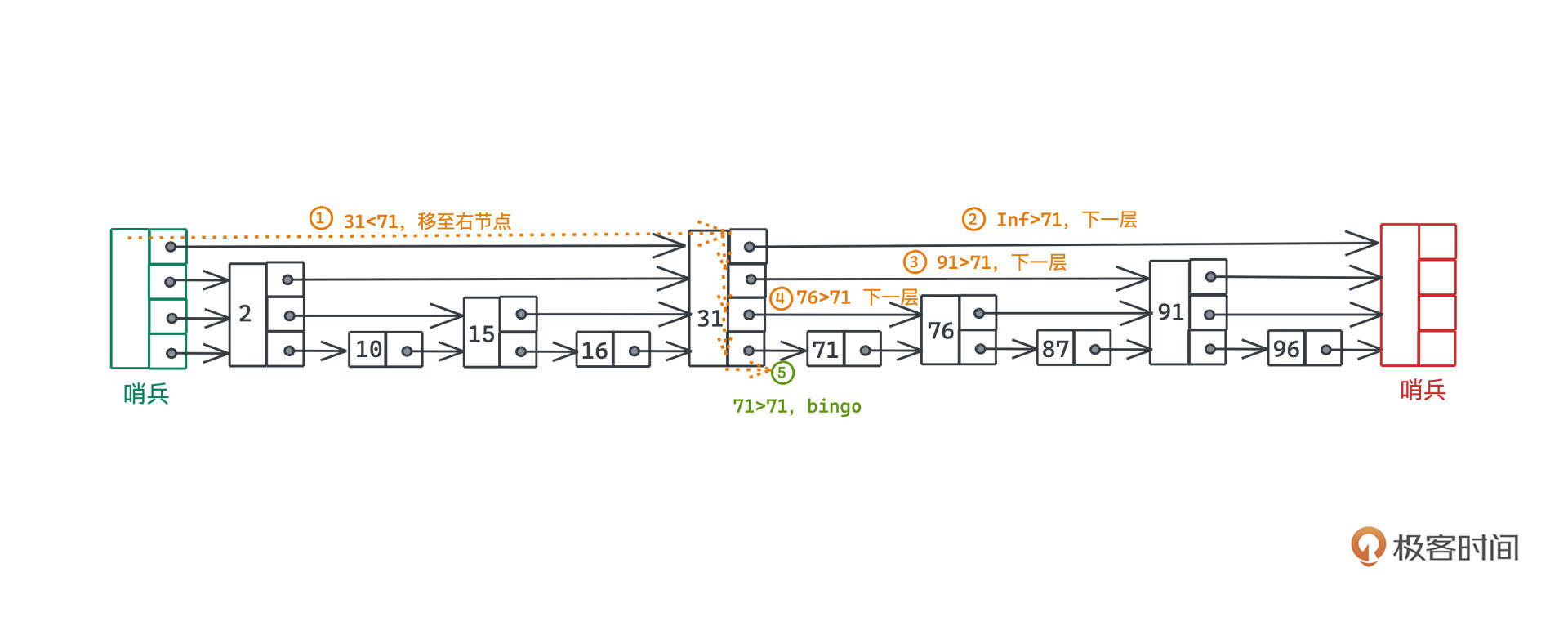
这样我们寻找某个元素的时候,就可以像换乘公共交通一样,先坐站距更远的交通工具,再换站距更小的交通工具,最后一段可能就是徒步,整个搜索效率就会高很多。比如这个具体的例子,假设我们想搜索的是71这个节点(例子来源于CMU的课件):
在原始的链表中,我们需要逐个遍历,需要进行6次跳跃。如果采用了跳表这样分层链表的存储方式,沿着指针移动的过程,可以减少为了2次。
当然,我们还是需要做一些next指针大小的判断,具体的搜索过程从高到低,每次比较包括三条分支:
- 如果当前指针指向的值为target,说明找到,返回即可;
- 如果当前指针指向的右节点的值大于target,我们进入更低的一层;
- 如果当前指针指向的右节点的值小于等于target,我们将指针移动到右节点。
整个过程直至搜索到最低一层,如果仍然没有搜索到,说明元素不存在。
图中你会看到整个链表的左侧和右侧还有一个绿色和红色的节点,我们一般称为哨兵,和之前讲的链表的哑节点起到一样的作用,帮助我们用更统一、更简短的逻辑来处理边界条件。
看到这里,你应该很容易直观地感受到采用分层链表在检索上的优势吧。本质上来说,高层的链表和线性索引的原理是很像的,我们就是通过为原始的链表增加了不同层的索引,起到了和平衡二分搜索树一样的快速搜索的效果。
跳表实现原理
设计想法很好,现在真正的问题来了:我们如何维护这样的多层链表结构?如何在合适的时机里加入新的层,以保证既可以高效查询,又不至于带来太高的维护成本呢?
跳表节点定义
我们先回答第一个问题,跳表节点的基本数据结构。
由于搜索是从高层往底层进行的,基本上就是一个从左上到右下的过程,所以跳表的每个节点,至少需要一个右向指针和一个可以表示层的数据结构。
如果简单地用一个链表表示,那就还需要引入一个下向的指针。当然,跳表需要存储元素,通常是一组键值,键是任意可比较的类型。为了方便实现,我们就假设元素只存储键,且必须是int类型,直接用val来表示。
写成C++的话,整个跳表节点的定义如下:
struct Node
{
// 至少需要向右、向下指针
Node* right;
Node* down;
int val;
Node(Node *right, Node *down, int val)
: right(right), down(down), val(val){}
};
有了这样向下和向右的指针,我们就可以维护整个多层的跳表结构了,也可以顺着指针进行前面说的查找过程了。
整个从左上到右下的搜索过程翻译成代码如下,我写了比较详细的注释供你参考:
bool search(int target)
{
Node *p = head;
while(p)
{
// 左右寻找目标区间
while(p->right && p->right->val < target)
{
p = p->right;
}
// 没找到目标值,则继续往下走
if(!p->right || target < p->right->val)
{
p = p->down;
}
else
{
//找到目标值,结束
return true;
}
}
return false;
}
完美跳表
继续看第二个问题,跳表每一层间距到底是多少合适呢?
其实最理想状态下,跳表所用的存储空间和查询过程,应该和二叉树是非常像的,我们会要求每一层都包含下一层一半的节点,且同一层指针跨越的节点数量是一样的。
所以基于和二叉树一样的原因,层数一共是logN层,在每一层中,我们最多只会进行一次跳跃,这是因为如果需要跳跃两次的话,我们在上一层判断的时候就会选择直接右跳,而不是下跳。因此每一层我们最多访问两个节点。整体搜索时间复杂度为O(logN),我们上面举的例子其实就是一个完美跳表。
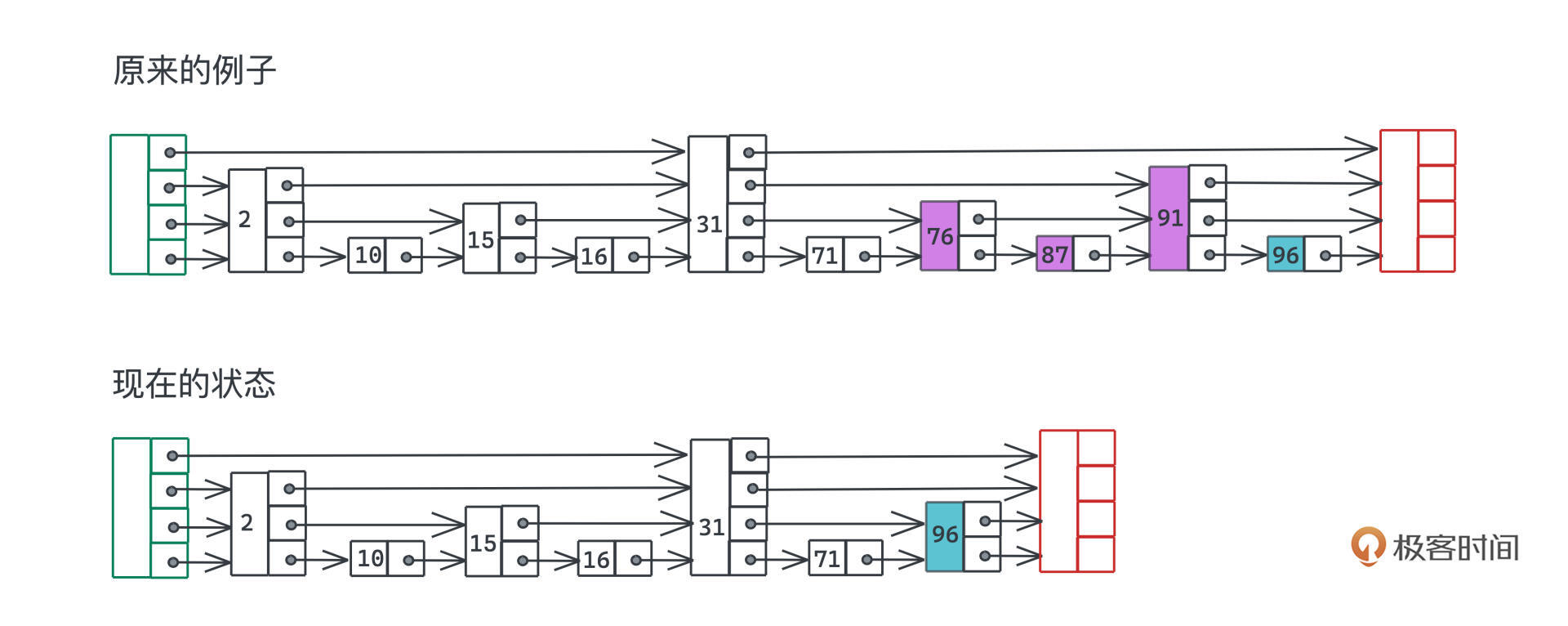
但是完美跳表有一个非常显著的问题:在有序集合动态插入和删除的过程中,我们很难高效地维护这样的结构。比如下图也是一个完美跳表,满足每一层的节点数量是下一层的一半,且中间的每个元素都被上一个例子所包含。
所以我们可以认为,这个状态是上一个例子的前置状态之一,也就是说在这个跳表中,只需要顺次添加76、87、91三个元素,理论上就应该得到上一个例子的跳表。
但是事实上你会发现,如果要维持完美列表,每一层的间距是一样的,我们就需要不断地调整每一个节点的层数,因为这个层数完全取决于该节点处于链表中的第几个位置。比如上图中的96的层数就有所变化。
随着不同的插入顺序,我们最差可能需要在某次插入中重置大部分节点的指针关系,这样的更新的维护成本显然不满足我们的期望,在引入了完美跳表的约束后,链表的插入、删除优势荡然无存。那怎么办呢?
引入随机性
关键就是我们需要放弃不同层数里严格倍增的节点数量约束,而只是让每一层的节点数量,在期望上,满足均匀分配和倍增的关系即可。这样从时间复杂度和空间复杂度上来说,我们的期望值其实不会有变化,只是会有一定的小波动。
还记得快排吗?其实也是有一定随机性的算法,虽然最差的时间复杂度是O(n*n),但可以认为这样极度劣化的情况基本不会发生,所以我们认为快排的时间复杂度仍然为O(n*logn)。这里引入随机性的跳表也是一样的情况。
跳表和随机性相关的地方主要体现在插入过程。假设需要插入的节点值为val,具体过程我们先梳理一下,后面会结合具体例子加强理解。
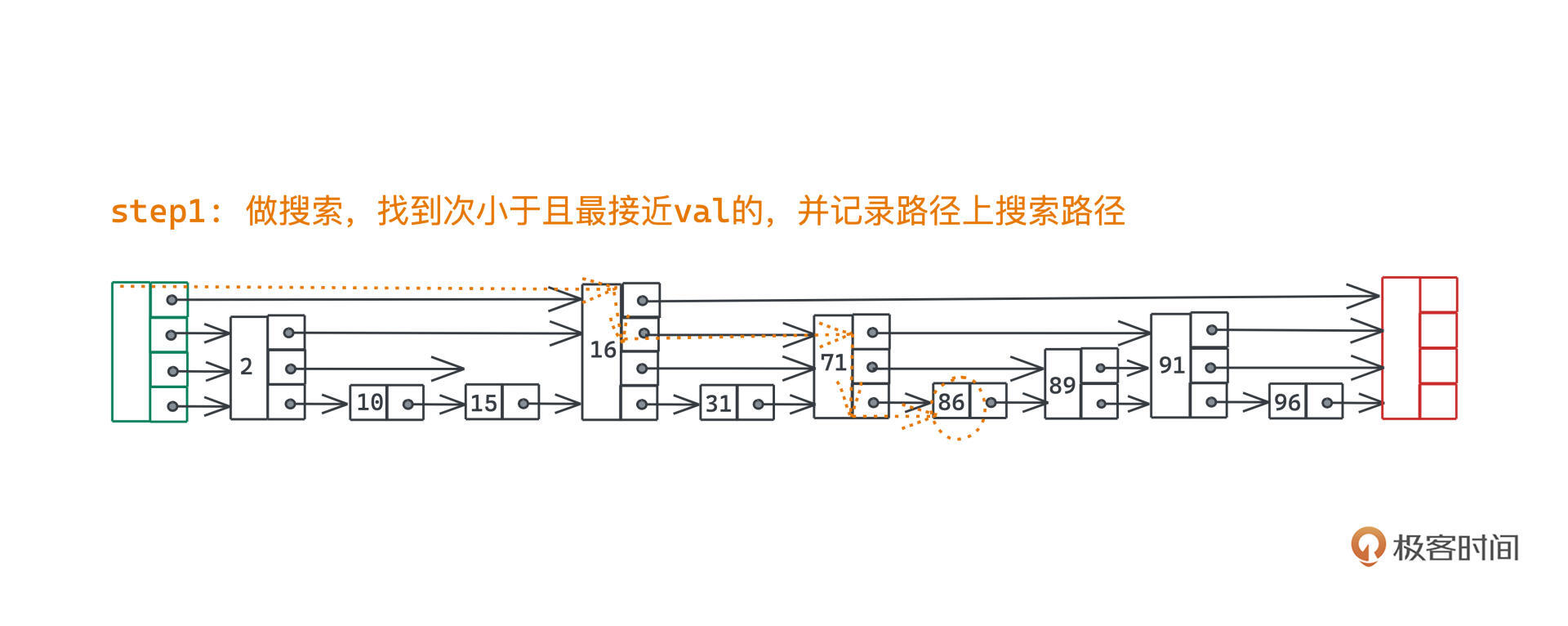
首先,我们进行一遍查找过程,也就是根据三个分支条件判断要么返回,要么向下移动,要么向右移动,直到找到某个次小于且最接近于val的节点。
其次,在搜索过程中,我们需要记录一下搜索路径,这个和DFS中记录路径的方式是一样的,每进到下一层前,把当前节点推入一个数组即可。
最后,随着搜索结束,我们一定会停留在跳表的最底层,且搜索指针指向的是最接近于目标值的节点,这个时候就需要进行真正的插入操作了。
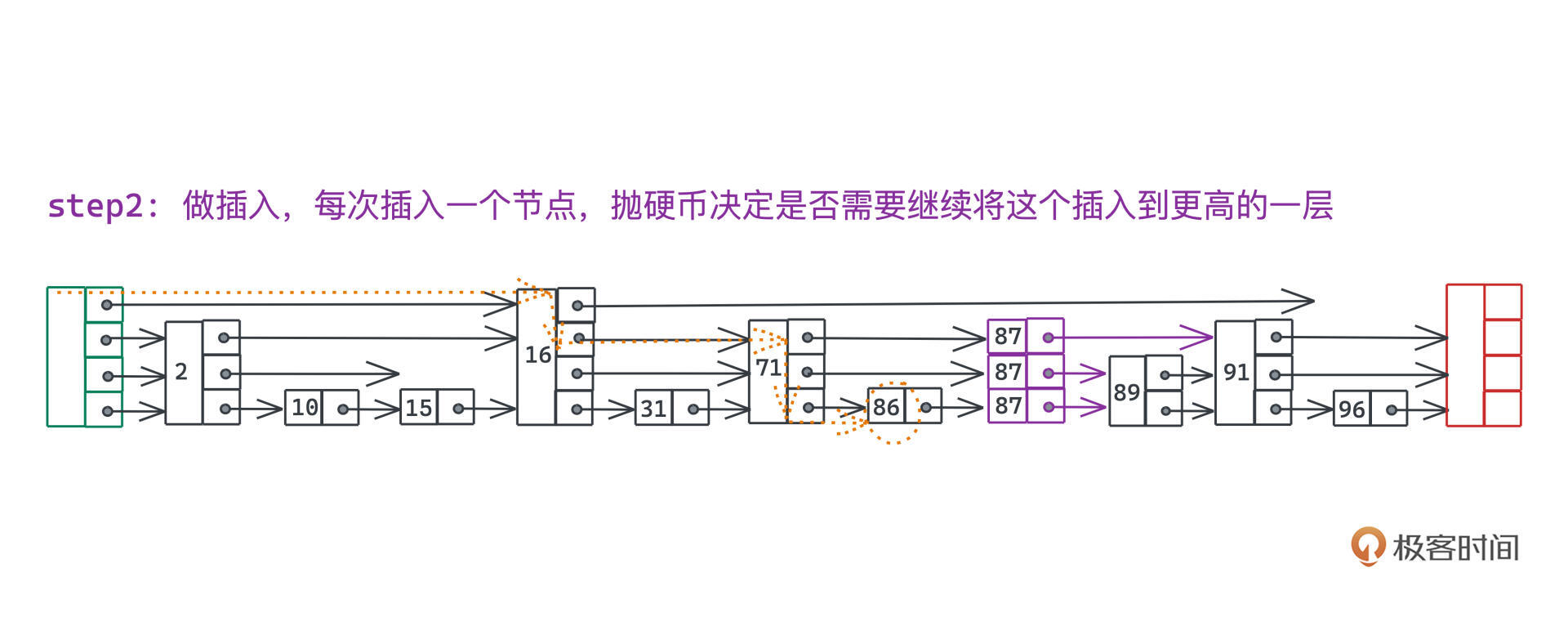
为了保证每一层的节点数量从期望上来说是上一层的两倍,每次插入一个节点的时候,我们可以采用抛硬币的策略,通过50%的概率决策,决定是否需要继续将这个插入到更高的一层。由于我们记录了整个路径,插入上一层的实现,也就是简单将一个新的节点插入到路径里上一层节点的右侧。简单算一下你就可以发现每个节点插入时在每一层的概率分别是:
- 第一层时100%会被插入(所有节点都出现在第一层)
- 第二层只有1/2的概率会被插入
- 第三层是1/4的概率会被插入
基于这样的策略,从期望上来说,层与层之间的节点数量自然就会满足期望倍增约束,且每个节点都不会有任何优待,每一层节点间的间距也比较均匀。到这里,多层的跳跃表结构也就完成了,在实际应用中达到了不输于红黑树的查询、插入、删除的效率。
看个例子
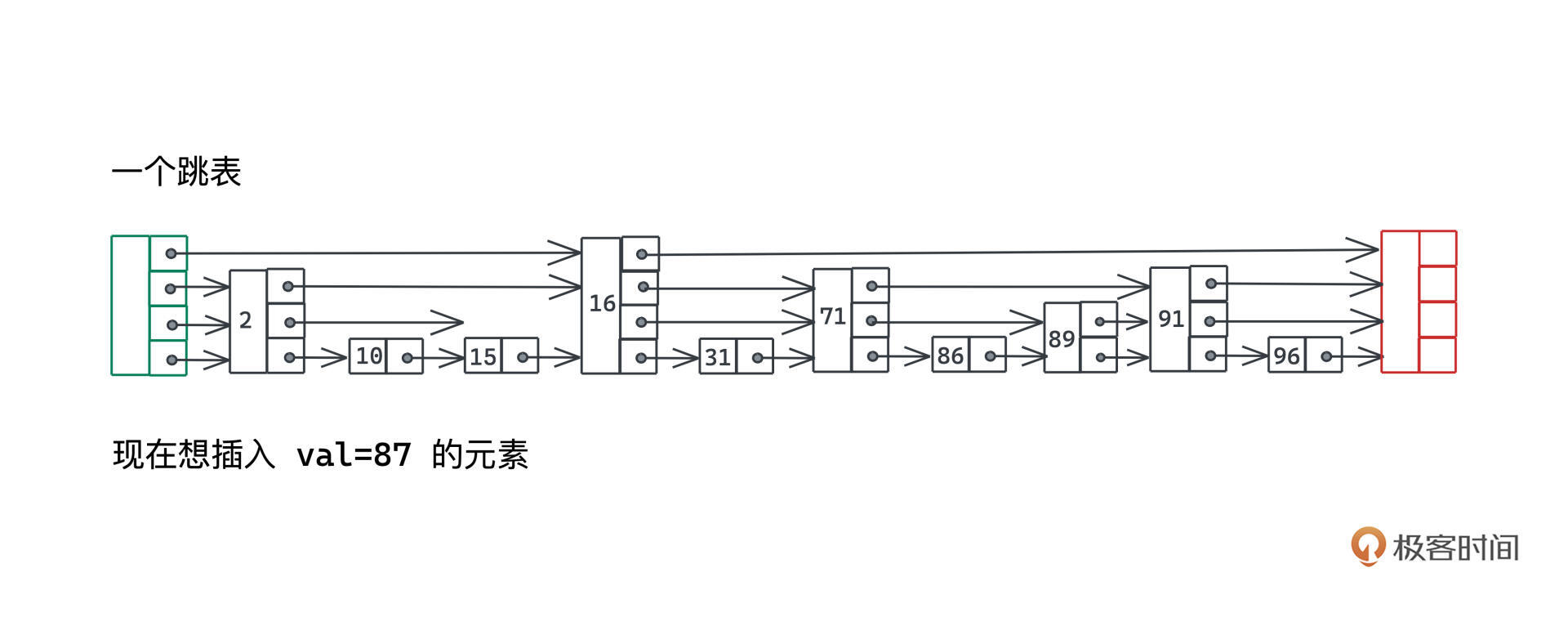
我们来看一个具体例子理解一下这个过程,比如我们希望插入val=87的元素:
第一步当然就是要做搜索,找到链表中离87最近的86,并记录路径上每一层的节点:
其次,需要将新建的87节点插入到86的右侧。按照抛硬币的策略,我们决定要不要往上一层继续添加该节点。比如我们连续抛了两次正面的硬币,第三次抛了反面,最终就只在1、2、3层中添加了87节点:
整个过程写成代码也不难,思路和前面说的完全一致,代码和注释供你参考。这里唯一需要注意的点就是,如果已经超过了目前的层数,但是抛硬币的结果还是正面,我们会在跳表中新建一层,其右节点为空,也就是该层只有这一个节点。
void add(int num) {
// 从上至下记录搜索路径
pathList.clear();
Node *p = head;
// 从上到下去搜索 次小于num的数字
while(p)
{
// 向右找到次小于num的p
while (p->right && p->right->val < num)
{
p = p->right;
}
pathList.push_back(p);
p = p->down;
}
bool insertUp = true;
Node* downNode = NULL;
// 从下至上搜索路径回溯,50%概率
// 这里实现是会保证不会超过当前的层数的,然后靠头结点去额外加层, 即每次新增一层
while (insertUp && pathList.size() > 0)
{
Node *insert = pathList.back();
pathList.pop_back();
// add新结点
insert->right = new Node(insert->right,downNode,num);
// 把新结点赋值为downNode
downNode = insert->right;
// 50%概率
insertUp = (rand()&1)==0;
// cout << " while new node " << num << " insertUp " << insertUp << endl;
}
// 插入新的头结点,加层
if(insertUp)
{
// cout << " insertUp new node " << num << endl;
head = new Node(new Node(NULL,downNode,num), head, -1);
}
}
删除的过程呢?相比于插入就简单很多。我们同样需要先找到该节点,但指针还是始终指向目标节点的左侧节点。在每层中,发现目标节点存在后,用当前节点指向右侧节点的右侧节点,和删除链表节点的写法是一致的,然后在后面的每一层都进行同样的操作,直到遍历完成。
总结
今天我们一起学习了Redis中有序集合的底层实现:跳表,作为字典类数据结构,它有着和红黑树、哈希表都不同的实现方式。
跳表,和红黑树一样,都提供了O(N)的空间复杂度,O(logN)的插入、查询、删除的时间复杂度,但实现起来比红黑树简单很多,通过引入随机性,我们只需要搜索并记录路径,就可以在保持跳表查询效率的同时,快捷地插入元素。这个操作比红黑树的旋转操作要简单很多。
虽然单点查询的效率确实不如哈希表,但跳表可以很好地支持范围查询,只要找到对应的范围节点,然后顺次在链表上遍历就可以了,这一点比红黑树也有明显优势。
可以认为在大部分方面,跳表都是非常有优势的有序集合实现方式,引入随机性从期望上保证效率、降低维护成本的思想也值得你好好体味。在力扣上的1206.设计跳表就是一个实现跳表的题目,你可以去上面试一试,平台给你提供了丰富的用例,能帮助你快速判断实现的正确性。
课后作业
今天的作业就是尝试实现一下跳表的删除操作,当然直接实现整个跳表是更好的,能帮助你复习一下链表的许多操作。
欢迎你在留言区留下你的实现,我们可以一起讨论。如果觉得这篇文章对你有帮助的话,也欢迎把这篇文章转发给你的朋友一起学习,我们下节课见~