16 KiB
01|动态数组:按需分配的vector为什么要二倍扩容?
你好,我是微扰君。今天我们进入第一章基础数据结构的学习。
计算机程序一直以来最根本的作用就是处理数据。即使在早期的计算机中,计算就已经不仅仅是几个数字之间的加减乘除那么简单了,经常需要处理大量线性存储的数据,一个很好的例子就是向量乘法。显然,我们需要找到一种合适的方式在计算机中存储这些信息,并能让我们可以快速地进行向量运算。
再举一个更工程化的例子。假设有个需求,我们希望只借助内存实现一个简易的银行账户管理系统,每个账号里包括两个基本信息:账户ID及余额。用户首次开户的时候,会被分配一个账户ID;系统要支持用户通过ID快速查询余额,也可以存款/取款改变自己的余额。
你可能会觉得这有什么难的?用数组就可以解决。建立一个整型动态数组,每来一个用户就给存到数组的某个位置,用该位置的数组下标来当用户的ID就行。查询起来更快,数组大小是动态的,也不用考虑用户数量超过容量上限的问题。
但是,基于下标随机访问数组元素为什么这么高效?动态数组是怎么做到看起来可以有无限容量?扩容机制的时间复杂度是多少,是不是会带来额外的内存浪费呢?不知道你有没有思考过这些问题。
今天,我们就带着这些问题一起学习第一种序列式容器vector,也就是动态数组。相信你学完之后,对这些问题的理解就深刻啦。
数组和内存
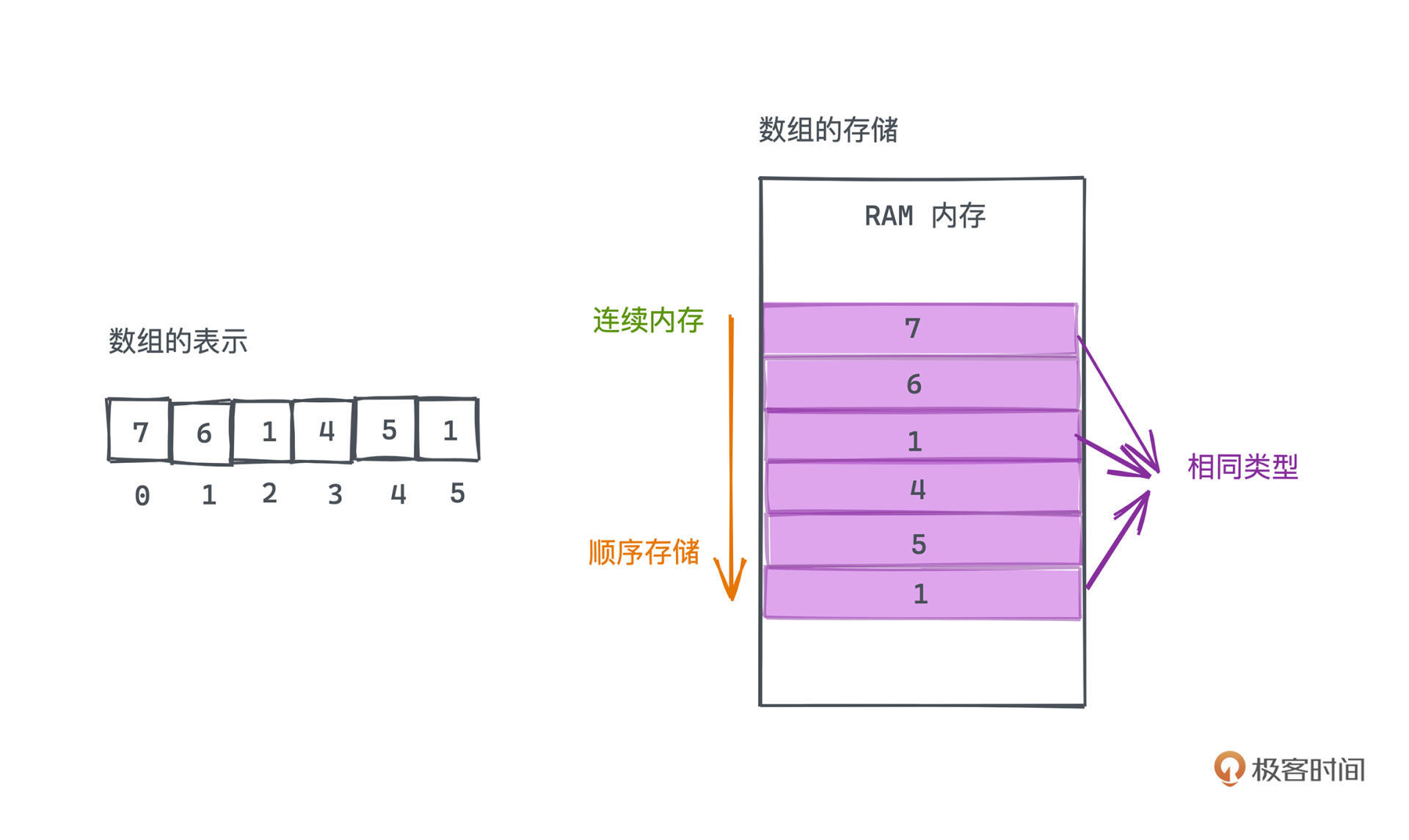
讲解动态数组的实现之前,首先要回顾一下数组是什么,不过为了和动态数组区分开来,我们常常也称之为静态数组。可以这样定义:静态数组是由相同类型的元素线性排列的数据结构,在计算机上会分配一段连续的内存,对元素进行顺序存储。
其中有三个关键词,相同类型、连续内存、顺序存储。之所以这样设计,本质就是为了能做到基于下标,对数组进行O(1)时间复杂度的快速随机访问。
存储数组时,会事先分配一段连续的内存空间,将数组元素依次存入内存。因为数组元素的类型都是一样的,所以每个元素占用的空间大小也是一样的,这样我们就很容易用“数组的开始地址+index*元素大小”的计算方式,快速定位到指定索引位置的元素,这也是数组基于下标随机访问的复杂度为O(1)的原因。
为什么要事先分配一段内存呢?答案也很简单,因为内存空间并不是无限的。一段程序里可能有很多地方都需要分配内存,我们必然要为分配的连续内存寻找一个边界。
事先确定数组大小并分配相应的内存给数组,就是告诉程序,这块地方已经是某个数组的地盘了,就不要再来使用了。同样,访问该数组的时候,下标也不应该超过地盘的范围,在大部分语言里这样的非法操作都会引起越界的错误,但在一些没有越界保护实现的语言(比如C语言)中,这就是一个很大的问题,需要开发者非常谨慎。有时这甚至会成为软件被黑客攻击的漏洞。
静态数组的特性
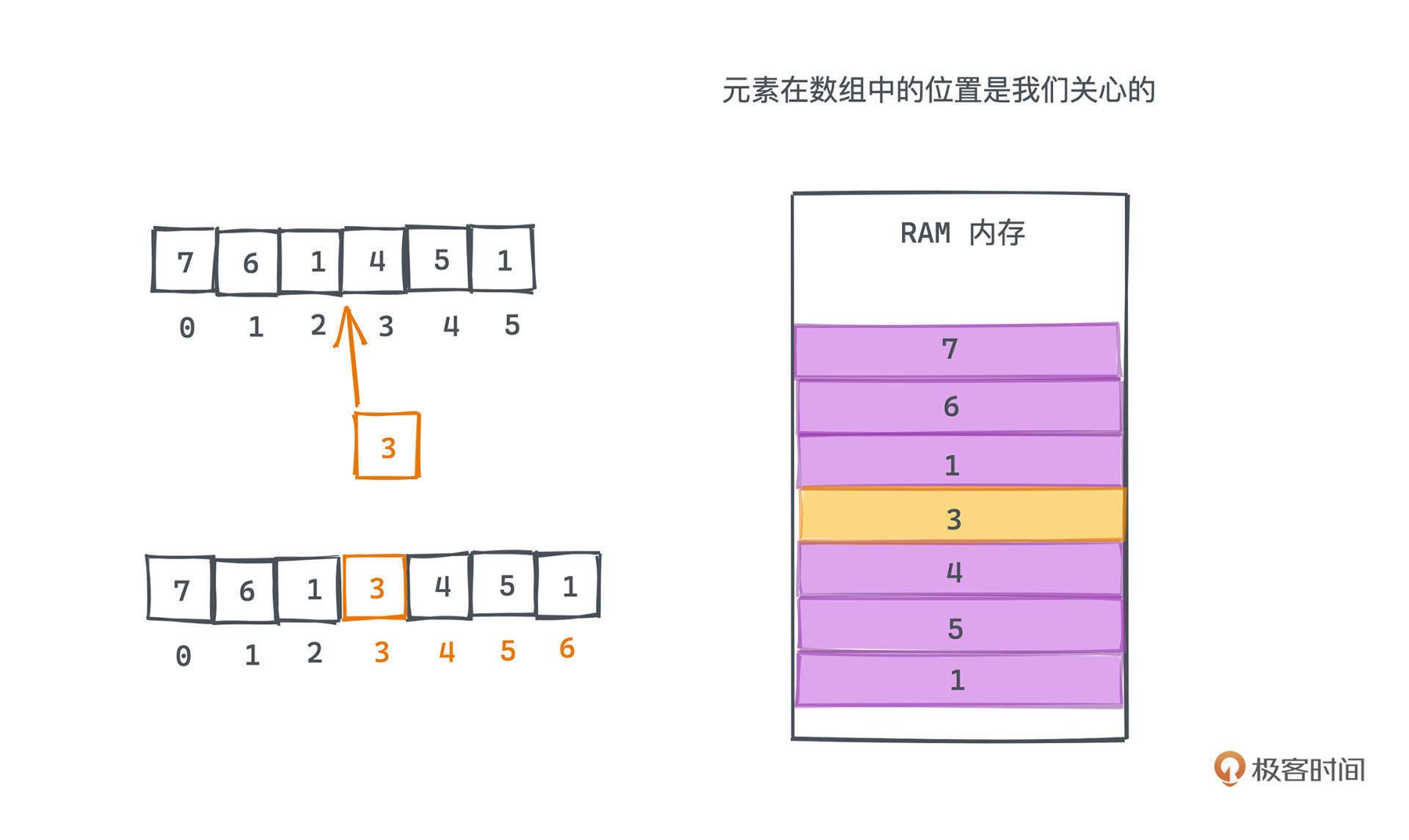
当然,在内存里这样的顺序存储也不是没有代价,这直接导致了数组的插入和删除会低效很多,平均的复杂度是O(N)。因为数组,和集合不同,元素在数组中的位置是我们关心的。
在长度为N的数组中,要在下标为T的位置插入数据时,原数组中下标为T到N-1的元素都需要向后顺移一位,这需要遍历数组中共计N-T个元素,当然,如果希望插入到数组的末端,只需要做插入而不需要做任何移动操作。但同样,如果我们希望将新元素插入到数组最开始的位置,就要将原数组所有元素都向后移动了,这需要移动共计N个元素。
所以平均而言,数组的插入操作的时间复杂度为O(N)。删除操作基于类似的原因,复杂度当然也是O(N)。
总的来说,静态数组的特性就是数组中元素的个数是事先确定的,每个元素都有对应的索引,第一个元素的索引为0。因为每个元素在内存占用的空间是一样的,我们可以基于首元素的地址和目标元素的下标,直接定位到目标元素的位置。
动态数组
很显然,使用静态数组的时候需要事先指定空间大小,这并不是很让人们满意。因为静态数组的使用者分配完内存之后,数组空间就不再能扩展(或收缩)了。比如在开头的简易银行系统中,确定固定的数组大小带来的风险就是:当用户数不断上涨直至超过数组容量范围时,我们的系统就不能继续工作了。
唯一的解决方案只能是重新申请一个更大的数组。这个过程,如果自己手动实现,有相当多琐碎的操作,至少包括配置一整块更大的连续内存空间、将元素逐一拷贝至新空间,以及释放原本的空间。
而动态数组的意义就在于将这些繁琐的细节封装起来,给用户良好使用体验的同时,也兼顾效率。这就是为什么我们在大部分业务开发场景下,更多地采用动态数组容器,而不是原生的静态数组。
STL的Vector就是这样一种经过严格测试和实战检验的动态数组容器,我们下面来分析一下它的原理和实现。其他高级语言的动态数组容器的实现思路其实也是类似的,比如Java中的ArrayList等(后续我们也会用Java中的实现来讲解)。你搞清楚一个,其他的就很好理解了。
动态数组源码分析
当然,STL的源码涉及了许多高深的C++技巧,我们并不会展开讨论,会对源码做一些简单的调整方便你理解原理。这里也给你一个看源码的小建议,不要死抠细节。我个人看源码比较喜欢自顶而下的方式,先从大的模块暴露的方法和接口看起,而不是上来就开始研究小模块的实现细节。
比如学习STL源码中vector实现的时候,你会经常发现allocator相关的方法,如果你揪着它不放一路溯源,会发现allocator的底层实现也非常复杂,但是,大多数时候我们不需要这么做,只要理解清楚了allocator的哪些方法用来申请内存、哪些方法用于释放内存,具体实现细节暂时当作黑箱,把精力集中在当下要搞清楚的问题上就可以了。
首先,来看vector在内存中的表示。它有两个指标,大小和容量。
大小,表示现在存了多少数据。存数据的部分其实和静态数组是一样的,都是一段连续的内存空间顺序排列这若干类型相同、大小一致的元素,但不同的地方在于,数组的大小是可以动态调整的。
我们知道,向计算机申请空间连续的内存空间是一个成本比较高的操作,不只需要扫描出堆区内存的空闲内存块,可能还需要向操作系统申请更大的堆空间,并产生用户态-内核态的切换成本。
所以为了减少二次分配的次数,初次配置空间的时候,可以分配比vector目前所需空间更多一些,后续的若干次插入就不再需要触发昂贵的扩容操作了。这样的可用空间,我们称为vector的容量,是vector在创建时需要的第二个可选参数。
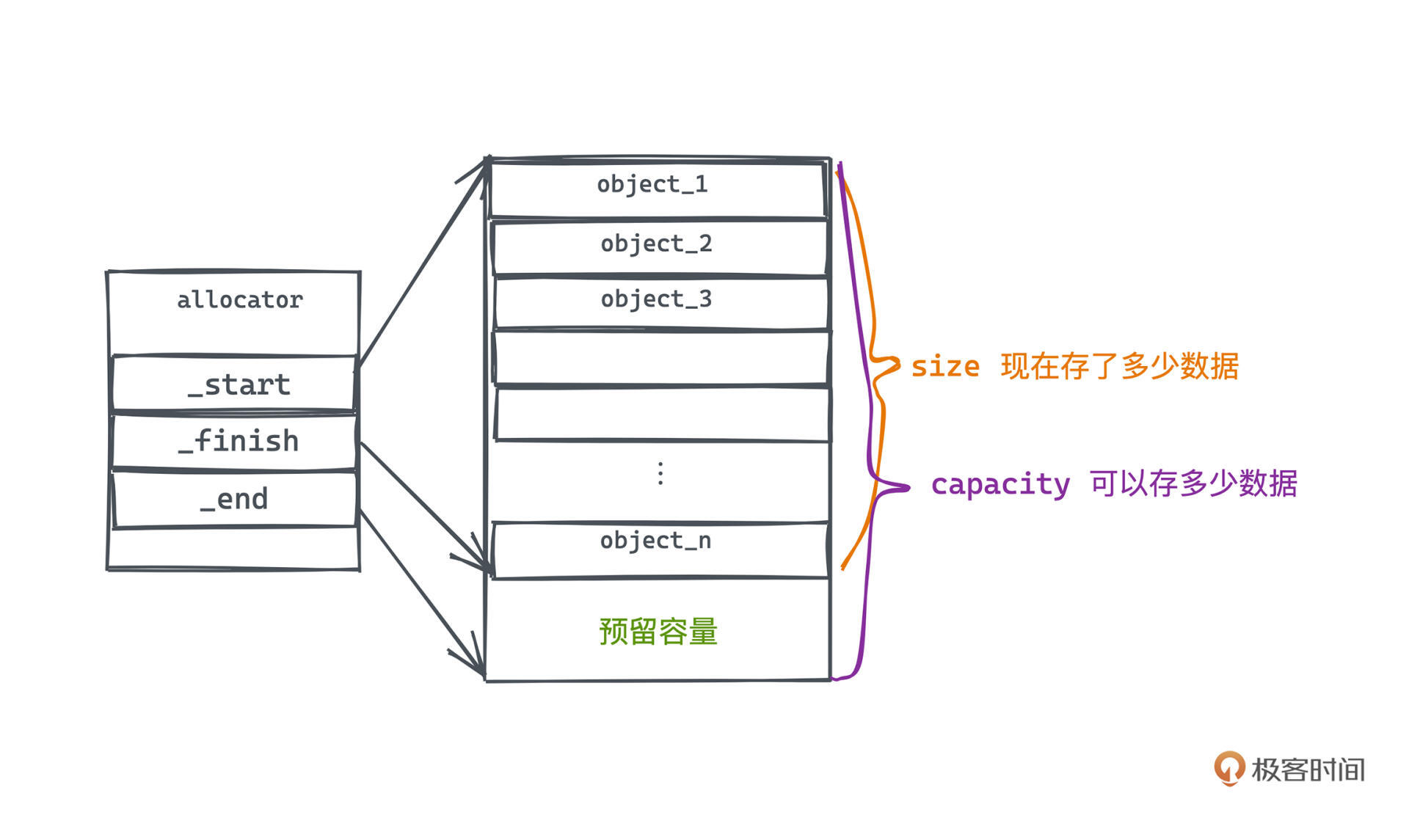
所以我们可以用三个指针来标记vector空间的使用情况,分别是:
- _start 指针,指向vector第一个元素
- _finish 指针,指向vector最后一个元素
- _end 指针,指向vector预留容量的边界
当然,动态数组的两个核心指标就很容易计算出来了:
- 容量,capacity = _end - _first,表示目前的数组最多能存储多少个元素
- 大小,size = _finish - _first,表示数组当前已经存储的元素个数
对应的代码如下:
template <class _Tp, class _Alloc = __STL_DEFAULT_ALLOCATOR(_Tp) >
class vector : protected _Vector_base<_Tp, _Alloc>
{
...
protected:
_Tp* _M_start; //表示目前使用空间的头
_Tp* _M_finish; //表示目前使用空间的尾
_Tp* _M_end_of_storage; //表示目前可用空间的尾
...
};
你不用太关注模版相关的语法,只需要知道这里protected的三个变量就是前面提到的3个指针。
有了这些,我们就可以判断什么时候需要触发扩容操作,以及扩容的方式。因为vector创建的时候会给一个容量,但随着我们不断往数组中插入元素,数组的大小终究会超过当前分配的容量,于是需要重新分配更大的内存,那具体分配多少是一个比较合理的值呢?
STL的扩容方法
来看一下STL怎么做的。除了查询已有资料之外,我个人比较推荐动手实验,不仅能随时检验自己脑海里的想法,通过动手实践对原理的理解和印象也更深刻一些。所以我们来编写一些测试方法,观察Vector在测试过程中的行为,再和官方文档及资料进行对比验证。
要做的实验也很简单,就是往一个数组里不断的插入元素,并观察size和capacity的变化。完整的代码可以在这里找到。
vector<int> v;
for (int i = 0; i < 20; i++) {
cout << "size: " << v.size() << " capacity " << v.capacity() << endl;
v.push_back(i);
}
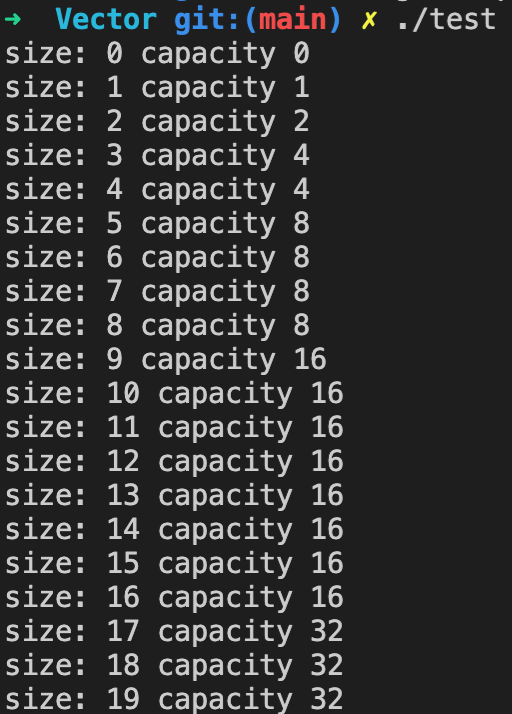
通过实验我们能发现一个很明显的规律:如果每次只插入一个元素,当vector的大小小于容量时,容量不会发生变化,数组大小不断递增。而当vector的大小即将超过容量的时候,插入之后,容量大小会翻番。
所以,倍增就是vector的扩容方式,这种类似倍增的策略也会出现在许多其他使用场景中。
这里很自然会有一个问题,为什么每次扩容时候都是以倍增的方式扩容,而不是增加固定大小的容量呢?
在回答这个问题之前,我们先看一看STL扩容逻辑的实现。
void push_back(const _Tp& __x) {//在最尾端插入元素
if (_M_finish != _M_end_of_storage) {//若有可用的内存空间
construct(_M_finish, __x);//构造对象
++_M_finish;
}
else//若没有可用的内存空间,调用以下函数,把x插入到指定位置
_M_insert_aux(end(), __x);
}
template <class _Tp, class _Alloc>
void
vector<_Tp, _Alloc>::_M_insert_aux(iterator __position, const _Tp& __x)
{
if (_M_finish != _M_end_of_storage) {
construct(_M_finish, *(_M_finish - 1));
++_M_finish;
_Tp __x_copy = __x;
copy_backward(__position, _M_finish - 2, _M_finish - 1);
*__position = __x_copy;
}
else {
const size_type __old_size = size();
const size_type __len = __old_size != 0 ? 2 * __old_size : 1;
iterator __new_start = _M_allocate(__len);
iterator __new_finish = __new_start;
__STL_TRY {
__new_finish = uninitialized_copy(_M_start, __position, __new_start);
construct(__new_finish, __x);
++__new_finish;
__new_finish = uninitialized_copy(__position, _M_finish, __new_finish);
}
__STL_UNWIND((destroy(__new_start,__new_finish),
_M_deallocate(__new_start,__len)));
destroy(begin(), end());
_M_deallocate(_M_start, _M_end_of_storage - _M_start);
_M_start = __new_start;
_M_finish = __new_finish;
_M_end_of_storage = __new_start + __len;
}
}
这段扩容操作在push_back和insert操作中都会触发,我们以简单一点的push_back,也就是往数组尾部插入元素的操作为例,来解释扩容的逻辑。
可以看到,push_back的时候会先做一个判断,看当前的容量是不是不够用了。如果够用,我们只要直接往后插入一个元素;不够用,才进行_M_insert_aux扩容并插入的操作,插入后需要把finish指针往后移动。这里在容量够用的时候,插入逻辑用的是construct函数,是STL容器中通用的构造方法。
我们来重点分析扩容逻辑所在的_M_insert_aux方法:
- 13-20行,实际上是因为还有其他函数会调用这个方法,我们已经确定容量不足,所以不会进入这段逻辑。
- 22-25行,主要做的事情就是读取原有的vector大小old_size,再从内存里申请一段新的空间,大小为2*old_size,创建新的首尾指针并指向新的空间。
- 26-31行,将老空间里的数据逐一搬到新的空间里,并在最后添加新的元素。这样就完成了扩容的主要目的,这是一个O(n)复杂度的操作,因为你需要对原数组进行逐一的深拷贝。
- 最后,在32-38行,我们需要做一些清理和收尾工作,释放掉老的数组空间和指针,将容器的首尾及容量指针都更新到对应的位置。
这样Vector就完成了对扩容操作的封装,是不是其实并不复杂呢?
现在清楚扩容的具体实现之后,来解答前面的问题:为什么扩容是采用倍增的方式,而不是每次扩展固定大小?这背后其实是有严密数学依据的,非常有趣,我们一起来探索一下。
用极端法来考虑这个问题。
先假设是不是可以不倍增,而是每次只扩展一个元素呢?直觉上这当然是不合理的,这会导致每一次插入都会触发扩容,而每次扩容都会进行所有元素的复制操作。所以如果我们要插入n个元素,需要进行的拷贝次数:
1+2+3+… +n=n^{2}
复杂度为O(n^2),均摊下来每次操作时间复杂度就是O(n)。
那如果我们不是每次只拓展一个元素,而是每次扩展C的容量,对复杂度的计算会产生多大的影响呢?同样来计算一下,每插入C次就需要进行一次扩展操作,每次扩展仍然需要复制全部元素,所以总的拷贝次数是:
C + 2C + 3C + … + floor(n/C) = n^{2}
复杂度同样为O(n^2) 。均摊下来每次操作时间复杂度还是O(n)。 虽然次数少了C倍,但仍然不令人满意。
更好的做法就是和STL一样采用倍增的思想,每次都将容量扩展为当前的一倍,它往往能让我们的时间复杂度下降很多。
算一下倍增这种策略下需要拷贝的次数:假设一共还是插入N次,那总拷贝次数,就是从1加到2的X次,其中x是logn向上取整;这是因为容量每次都在翻番,所以每次触发拷贝的时候,容量分别是1、2、4、8 … 一直到logn向上取整。
1+2+4+8+… +2^{x}=2^{(x+1)}-1
这样插入N个元素的复杂度就一下减少为O(N)了。均摊到每次插入的扩容复杂度就为O(1),这当然是一个令人满意的结果啦。
总结
相信经过今天的学习,你一定已经对开头的几个问题有答案了吧,简单总结一下。数组,是支持O(1)基于下标随机访问的数据结构,在内存中是连续存储的。基于下标高效访问元素的核心就在于“相同类型”和“连续存储”的特性,当然,也带来了高昂的插入和删除的时间复杂度。
动态数组之所以能看起来像是无限容量,也仅仅是因为它内置了倍增的扩容策略,每次数组大小超过容量的时候,就会触发数组的扩容机制,封装了繁琐的拷贝细节。
也正是因为上述特性,动态数组广泛应用在需要经常查询、变更,但是很少插入/删除的场景,比如我们在实现一个简单的Web服务器的时候,可以用vector来存储handler的线程,达到线程复用的效果。
你应该感受到了今天的内容比上一讲的文本差分要简单一些,是的,接下来我们会先把数据结构实现的基础打好,了解清楚背后的实现原理,这样在日常开发中,不同的数据结构可能造成什么样的性能瓶颈,你都能烂熟于心。
课后作业
我们已经细致地分析了在vector中插入元素的方法,如果要删除一个元素应该怎么实现呢?在删除元素的时候需不需要缩容呢?如果需要的话,你会怎么做。
这是一个开放问题,欢迎你在留言区与我讨论。我们下节课见。