17 KiB
09 |测试结果不显著,要怎么改善?
你好,我是博伟。
通过“基础篇”的学习,你已经掌握了A/B测试的整体流程,那就可以参照这些流程设计一次A/B测试了。不过在具体实施的过程中,你会因为业务的复杂性、没有严格遵守规范的流程,或者数据本身的属性等,不可避免地遇到一些问题。
没错儿,这就是我在开篇词中和你说的,A/B测试的实践性非常强,你需要能够识别那些潜在的坑,并找到相应的解决方法。所以在接下来的三节课里,我会带你去看看我积累的经验,曾经踩过的坑,让你在实践时能提前规避,少出错。
今天,我们就先从一个很痛的问题开始吧。在第7节课我们学习如何得到可信赖的测试结果,以及如何分析测试结果时,非常顺利地得出了对照组和实验组指标显著不同的结果。不知道你脑海中会不会一直萦绕着这么一个问题:我也是按照这个流程来设计A/B测试的啊,为什么我的实验结果不显著呢,我应该据此得出“两组指标事实上是相同的”结论吗?
今天这节课,我们就来深入剖析“测试结果如何不显著怎么办”这个大家经常遇到的问题。
为什么会出现“实验结果不显著”?
首先我们要搞清楚,为什么会出现“实验结果不显著”?有两方面原因。
- A/B测试中的变化确实没有效果,所以两组的指标在事实上是相同的。
- A/B测试中的变化有效果,所以两组的指标在事实上是不同的。但是由于变化的程度很小,测试的灵敏度,也就是Power不足,所以并没有检测到两组指标的不同。
如果是第一种原因,就证明这个变化对产品/业务优化没有效果。那我们要考虑放弃这个变化,或者去测试新的变化。
如果是第二种原因,那我们可以从A/B测试的角度进行一些优化和调整。具体来说就是,通过提高Power来提高A/B测试检测到实验结果不同的概率。在第6节课我讲过了,Power越大,越能够准确地检测出实验组与对照组的不同。所以当我们提高了Power之后,如果仍然发现测试结果不显著,这样才能得出“两组指标事实上是相同的”的结论。
有什么方法可以提高Power呢?
我们再来回顾下第6节课讲到的样本量估算公式:
\\mathrm{n}=\\frac{\\left(Z\_{1-\\frac{\\alpha}{2}}+Z\_{1-\\beta}\\right)^{2}}{\\left(\\frac{\\delta}{\\sigma\_{\\text {pooled}}}\\right)^{2}}=\\frac{\\left(Z\_{1-\\frac{\\alpha}{2}}+Z\_{\\text {power}}\\right)^{2}}{\\left(\\frac{\\delta}{\\sigma\_{\\text {pooled}}}\\right)^{2}}
其中:
Z\_{1-\\frac{\\alpha}{2}} 为 \\left(1-\\frac{\\alpha}{2}\\right) 对应的 Z Score。
Z\_{\\text {Power}} 为 Power 对应的 Z Score。
\\delta 为实验组和对照组评价指标的差值。
\\sigma\_{\\text {pooled}}^{2} 为实验组和对照组的综合方差 (Pooled Variance)。
在公式里,我们找出影响Power的因素,也就是样本量和方差。其中:
- 样本量和Power成正比。即通过增大样本量就可以提高Power。
- 方差和Power成反比。即通过减小方差就可以提高Power。
具体来说,实践中,在有条件获得更大样本量的情况下,可以选择增大样本量的方法来提高Power,相对简单易操作。如果受流量或时间限制,没有条件获得更多的样本量,此时可以通过减小方差来提高Power。
接下来,我就分别从增大样本量和减小方差这两个维度,来讲解6种提高Power的具体方法。
如何通过增加样本量来提高Power?
实践中,用来增加样本量的方法主要有三种:延长测试时间,增加测试使用流量在总流量中的占比,以及多个测试共用同一个对照组。
延长测试时间
对于延长测试时间,你肯定不陌生,我在第6节课讲样本量估算时就讲过。每天产生的可以测试的流量是固定的,那么测试时间越长,样本量也就越大。所以在条件允许的情况下,可以延长测试的时间。
增加测试使用流量在总流量中的占比
假设某个产品每天有1万流量,如果我要做A/B测试,并不会用100%的流量,一般会用总流量的一部分,比如10%,也就是测试使用流量在总流量中的占比。
为什么不使用全部流量呢?
一方面,A/B测试有试错成本,虽然出现的概率较低,但是我们在测试中做出的任何改变都有可能对业务造成损害。所以,使用的流量越少,试错成本越低,也就越保险。
另一方面,在大数据时代,对于互联网巨头来说,由于本身就拥有巨大的流量,那么产品本身做出的任何比较明显的改变,都有可能成为新闻。
比如要测试是否要增加一个新功能时,公司并不想在测试阶段就把这个新功能泄露给用户,以免给用户造成困扰。所以它们一般会先使用很小比例的流量来做A/B测试(比如1%),确定得到显著结果后再把A/B测试中的变化慢慢推广到100%的流量。
所以,在保持测试时间不变的情况下,还可以通过增加测试使用流量在总流量中的占比,来达到增加样本量的目的。
多个测试共用同一个对照组
有时我们会在同一个产品上同时跑多个A/B测试,比如我们想要提升推送的点击率,就会在原推送的基础上改变推送的标题、推送的内容、推送的时间、推送的受众,等等。
对于这四个不同的影响因素,事实上,改变每一个因素都是一个独立的A/B测试。那理论上我们就需要设计4个实验,需要有4个实验组和4个对照组。
假设我们现在的可用流量一共是8万,那么每组就有1万流量。但是你会发现这样流量的利用率太低了,因为每个实验的对照组其实都是一样的(原推送)。但如果我们把4个对照组合并成一个,这样的话就变成了4个实验组和1个对照组,每组就有1.6万流量。
你看,在同一个基础上想同时验证多个变化,也就是跑多个A/B测试有相同的对照组的时候,我们可以把对照组合并,减少分组数量,这样每组的样本量也会增加。这种测试又叫做A/B/n测试。
总结来说,在实践中:
- 如果时间允许,最常用的是延长测试时间的方法,因为操作起来最简单。
- 如果时间不充足的,可以优先选择增加测试使用流量在总流量中的占比,因为可以节省时间。
- 当有多个测试同时进行,而且对照组又相同的情况下,就可以把多个对照组合并成一个。
通过增加样本量来提高Power,是实践中最常见的方法,但是业务场景千变万化,虽然不常见,但有时候确实没有办法获得更多的样本,比如时间紧迫,同时已经使用了100%的总流量,结果还是不显著,那这个时候就要通过减少方差来提高Power了。
如何通过减小方差来提高Power?
实践中常用的减少方差的方法也有三种:减小指标的方差,倾向评分匹配,以及在触发阶段计算指标。
减小指标的方差
减小指标的方差有两种方式。
第一种方式:保持原指标不变,通过剔除离群值(Outlier)的方法来减小方差。
如果我们通过指标的直方图,发现实验的指标分布中有很明显的离群值,就可以通过设定封顶阈值(Capping Threshold)的方法把离群值剔除掉。
比如可以根据指标的分布,只选取95%的取值范围,然后把剩下的5%的离群值剔除掉。常见的指标,比如电商中的人均花费,或者音乐App中的人均收听时间,由于会有些极少热衷于线上购物的用户花费居多,或者音乐发烧友一直在听歌,那么这些极少部分的用户就可能变成离群值,从而增加方差。
第二种方式:选用方差较小的指标。
取值范围窄的指标比取值范围广的指标方差要小。比如点击者量比点击量的方差小(因为一个点击者可以产生多个点击,点击比点击者多,取值范围广);购买率比人均花费的方差小(因为购买率是表征买或不买的二元事件,只有两个取值,人均花费则可以是任何数量的金钱,理论上有无限的取值范围);收听率比人均收听时间的方差小;等等。
可以看到,对于表征类似的行为(比如买买买,听音乐,看视频,等等),概率类指标要比均值类指标的方差小。所以在满足业务需求的情况下,如果我们想要减少方差,就可以把均值类的指标转化成表征相似行为的概率类指标,也就是修改原定指标,选用取值范围窄的指标。
倾向评分匹配(Propensity Score Matching)
倾向评分匹配,简称PSM,是因果推断的一种方法,目的是解决实验组和对照组分布不均匀的问题。
你一定还记得我们在第7节课中,学习过分析结果前要进行合理性检验,那么它和PSM是什么关系呢?
我来总结下。如果说合理性检验是帮我们确定两组分布是否相似的方法,那么PSM,就是帮我们找出两组中相似部分的回溯性分析方法。简单来说,两组的各个特征越相似,就说明两组的方差越小。
PSM的基本原理,就是把一组中的数据点,找到在另一组和它们相似的数据点,进行一对一的匹配,这个相似性是通过比较每个数据点的倾向评分(Propensity Score)得到的。如果不理解倾向评分也没关系,你只需要知道这一点就够了:倾向评分越接近,说明两个数据点越相似。这里的一个数据点,指的就是A/B测试中的一个实验单位。
PSM的具体做法如下。
- 首先,把我们要匹配的两组中每个数据点的各个特征(比如用户的性别,年龄,地理位置,使用产品/服务的特征等)放进一个逻辑回归(Logistics Regression)中。
- 然后,算出每个数据点的倾向评分,然后再用诸如最邻近(Nearest Neighbor)等方法进行匹配。
- 最后我们只需要比较匹配后的两组相似的部分即可。
PSM的原理有些复杂,我放了一些资料链接,你可以查看。不过幸运的是,在主要的编程语言Python和R中都有相应的库,比如Python中的pymatch和R中的Matching,让我们的实施变得相对容易些。
在倾向评分匹配这个部分,你只需要记住一个结论就可以了,那就是:PSM能够有效地减少两组的方差**。**通过比较倾向评分匹配后的两组的相似部分,我们可以来查看结果是否显著。
在触发阶段计算指标
在A/B测试中我们把实验单位进行随机分组的这个过程叫做分配(Assignment), 同时你要知道,在有些A/B测试中,比如在第8节课的案例中,我们要测试的变化是需要满足一定条件才能触发的。
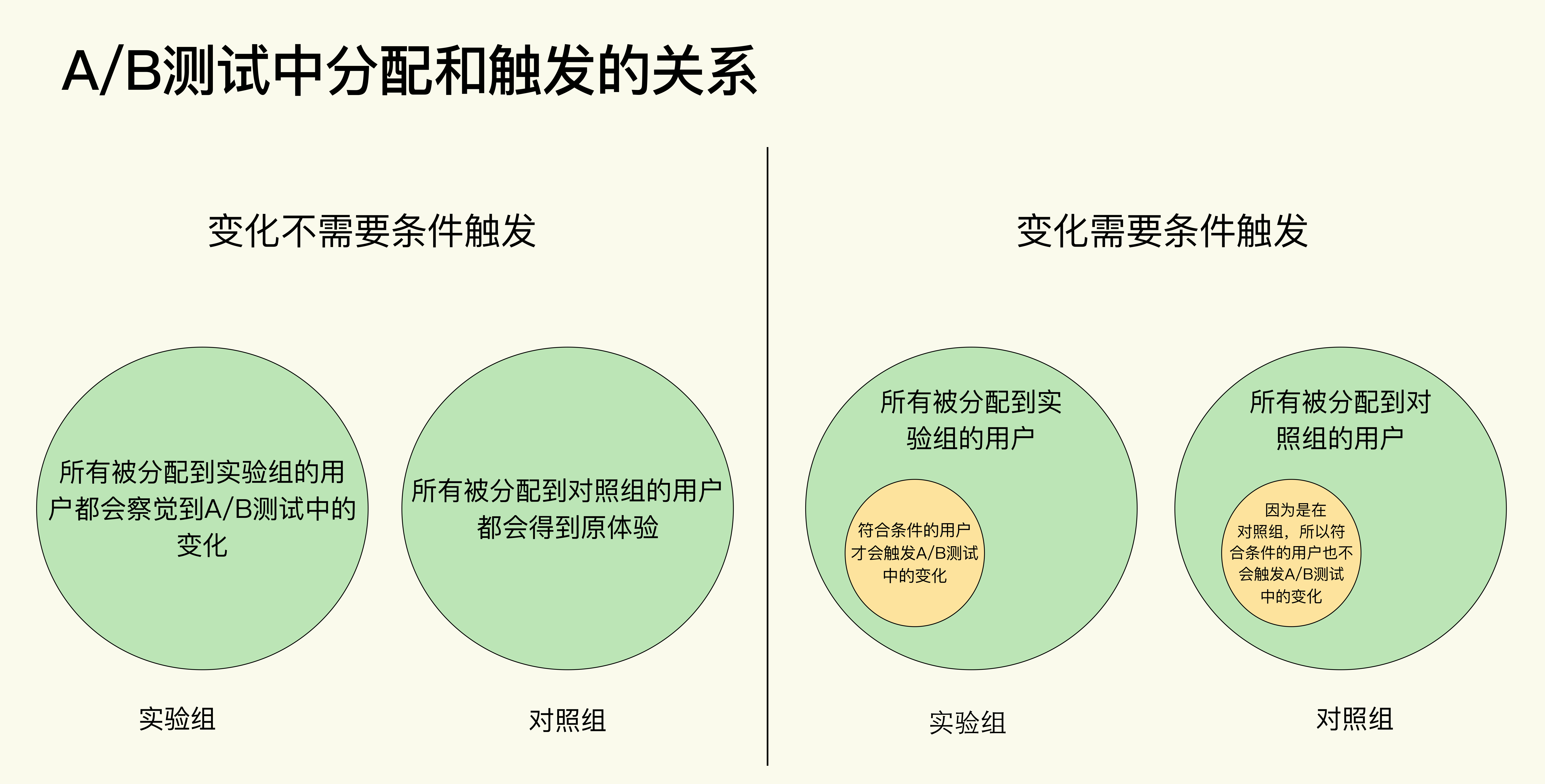
所以从分配和触发的关系来看,A/B测试可以分为两种。
-
变化不需要条件触发。所有用户在被分配到实验组后,就都可以体验到A/B测试中的变化。
-
变化需要条件触发。在被分配到实验组的所有用户中,只有满足一定条件的用户才会触发A/B测试中的变化。
实践中大部分的A/B测试都属于第一种,而且也比较好理解。
但是要注意了,我们这里讲的减小方差的方法只适用于第二种A/B测试,简单来说,就是在计算指标时只考虑每组符合触发条件(黄圆圈)的用户,而不是考虑每组中的所有用户(绿圆圈)。这个不是很好理解,我来举例说明下。
还记得第8节课中我们讲到可以利用弹窗的形式来告知用户“把喜欢的音乐加入收藏夹”新功能的A/B测试吗?在A/B测试的设计中,并不是在实验组的所有用户都会收到弹窗提醒的。
所以为了避免打扰到不相关的用户,把弹窗发送给需要这个功能的用户,我们事先规定了触发弹窗的规则:
- 该用户从来没用过“把喜欢的音乐加入收藏夹”这个功能。
- 该用户已经对某首歌听了4次,当播放第5次时触发弹窗。
那么当我们计算案例中的评价指标时,各组中“把喜欢的音乐加入收藏夹”功能的使用率 = 各组中使用了“把喜欢的音乐加入收藏夹”的用户总数 / 实验中各组的用户总数。
这里的分母“实验中各组的用户总数”就只算满足弹窗触发规则的用户,而不是算所有被分配到实验中各组的用户,这就是在触发阶段计算指标。
这里要注意的是,在对照组也会有用户满足弹窗触发规则的,只不过因为他们在对照组,所以即使他们满足了弹窗触发规则,我们也不会给这些用户发弹窗,我们还是要统计这些人因为要用他们做分母来计算评价指标。
这里对数据埋点熟悉的小伙伴可能要问了:这些符合弹窗触发规则的对照组用户并没有触发弹窗,在数据中并没有相关的记录,我怎么在数据中去记录他们呢?
在工程实现上其实是有一个小技巧的:对于对照组的用户,如果他们符合触发规则,我们就给他们发送一个只有一个像素点的看不见的隐形弹窗,这样的话我们在数据中会有相关记录,方便之后的指标计算,同时又保证了对照组不会受到弹窗的影响。
通过把评价指标的分母变为满足弹窗触发规则的用户,在计算指标时就会排除掉数据中的噪音(那些被分配到实验中但是没有触发弹窗的用户),从而减小方差。
这种需要触发的A/B测试多出现在有固定的用户使用路径的业务中,比如电商。在电商中,用户一般有较明确的多层级的使用路径:进入网站/App —> 浏览商品列表 —> 查看具体商品 —> 加入购物车 —> 购买。
在电商的A/B测试中,一般是在用户进入网站/App时就被分配到实验组或者对照组,如果我们测试之后的环节,比如在“购物车”页面测试新功能,这时候只有进入到“购物车”页面的用户才能触发A/B测试中的变化。
总体而言,通过减少方差来提高Power的情况不多(常见的是通过增加样本量来提高Power)。如果真的遇到这种情况,那么比较简单快速的方法就是减小指标的方差。当然如果有条件的话我还是推荐更加科学的倾向评分匹配(PSM)。那么对于在A/B测试中的变化存在触发的情况下,就一定要在触发阶段计算指标。
小结
为了解决A/B测试结果不显著的问题,这节课我们主要讲解了提高A/B测试Power的6种方法,我把它们从原理上分成了两大类:
你可以根据我对每种方法的介绍,以及在什么情况下选用哪种方法,灵活应用。
如果在尝试过这些方法后,重新跑实验得出的测试结果还不显著,那就说明两组的指标事实上是相同的,我们就要放弃这个A/B测试中的变化,用其他的变化来优化业务和产品。
最后再强调一下,做出一个能真正提升业务的改变并不容易。从美国FLAG这些大厂披露出来的实验数据来看,A/B测试得到真正显著的结果并最终实施变化的概率,还不到三分之一。
所以也不要气馁,虽然不是每次实验都会有显著的结果,但是你可以从每次实验中学到新的知识(比如变化到底对业务有没有效果),沉淀新的方法论,还能从中发现业务、数据或者工程上潜在的一些问题。这些个人技能上的成长、业务流程上的完善,都是非常宝贵的。
思考题
在某次A/B测试中,你是不是也遇到过没能得到显著结果的情况?你当时是怎么处理的,有没有从实验中获得一些宝贵的经验?
欢迎在评论区留言、讨论,也欢迎点击“请朋友读”,把今天的内容分享给你的同事、好友,和他一起学习、成长。好,感谢你的收听,我们下节课再见。