126 lines
15 KiB
Markdown
126 lines
15 KiB
Markdown
# 26 | 模型训练(上):决策树系列算法详解
|
||
|
||
你好,我是吴磊。
|
||
|
||
在上一讲,我们重点介绍了机器学习中的特征工程,以及Spark MLlib框架支持的特征处理函数。基于线性回归模型,我们对比了不同特征处理方法下的模型效果。一般来说,线性模型的模型容量比较有限,它仅适合拟合特征向量与预测标的之间存在线性关系的场景。
|
||
|
||
但在实际应用中,线性关系少之又少,就拿“房价预测”的项目来说,不同的房屋属性与房价之间,显然不是单纯的线性关系。这也是为什么在房价预测的任务上,线性回归模型的预测误差一直高居不下。因此,为了提升房价预测的准确度,我们有必要从模型选型的角度,着手去考虑采用其他类型的模型算法,尤其是非线性模型。
|
||
|
||
Spark MLlib框架支持种类丰富的模型算法,为了在减轻你学习负担的同时,尽量全面地覆盖其中的内容,我把模型训练分为了上、中、下三讲。今天这一讲,我们专注在决策树系列算法的讲解。
|
||
|
||
后面两讲我再结合房屋预测和电影推荐场景,带你在实践中掌握Spark MLlib模型算法,从而让你在不同的场景下得心应手地开展模型选型与模型调优。
|
||
|
||
## 课程安排
|
||
|
||
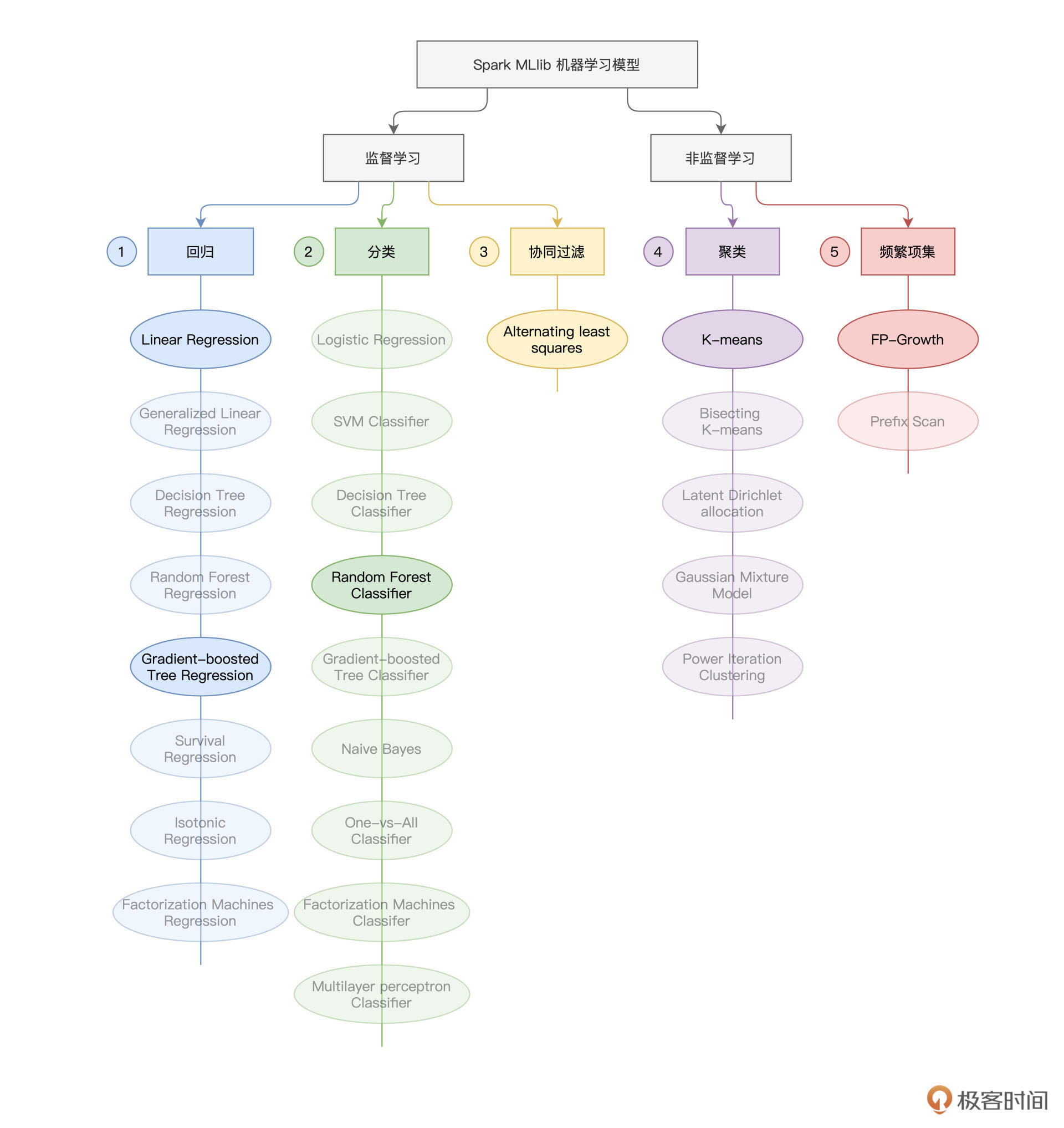
因为模型训练的部分内容比较丰富,为了让你有一个清晰的学习计划,咱们还是先来交代一下课程安排。在机器学习领域,如果按照“样本是否存在预测标的(Label)”为标准,机器学习问题可以分为监督学习(Supervised Learning)与非监督学习(Unsupervised Learning)。Spark MLlib同时支持这两大类机器学习算法,如下图所示。
|
||
|
||
|
||
|
||
可以看到,在Spark MLlib开发框架下,按照使用场景不同,监督学习又被细分为回归(Regression)、分类(Classification)和协同过滤(Collaborative Filtering);而非监督学习被细分为聚类(Clustering)与频繁项集(Frequency Patterns)。
|
||
|
||
不同的分类下,Spark MLlib支持的模型算法多样而又庞杂。如果逐一讲解每种算法的原理和用法,不但枯燥乏味,而且容易遗忘。所以,对于每个分类,我都会精选一个最具代表性的算法,再结合实例进行讲解,这样你学完之后印象会更加深刻。
|
||
|
||

|
||
|
||
与5个子分类相对应,模型训练课程的实例也有5个,分别是房价预测、房屋分类、电影推荐1、房屋聚类、电影推荐2。根据数据来源的不同,这5个实例又可以分为两类,如下图所示。
|
||
|
||
为了照顾基础薄弱的同学,我们需要先搞清楚决策树、GBDT(Gradient-boosted Decision Trees)和RF(Random Forest)这些前置知识。学完这节课之后,你会发现一个很有趣的现象,这些知识点背后的原理跟人类的决策过程惊人的相似,但相比人类经验,机器又能青出于蓝。
|
||
|
||
好啦,让我们正式开始今天的学习。
|
||
|
||
## 决策树系列算法
|
||
|
||
马上就是“双十一”了,你可能很想血拼一把,但一摸自己的钱包,理智又占领了高地。试想一下,预算有限的情况下,你会如何挑选一款手机呢?我们往往会结合价位、品牌、评价等一系列因素考量,最后做出决策。
|
||
|
||
其实这个依据不同决定性因素来构建决策路径的过程,放在机器学习里,就是决策树。接下来,我们用严谨一点的术语再描述一下什么是决策树。
|
||
|
||
决策树(Decision Trees)是一种根据样本特征向量而构建的树形结构。决策树由节点(Nodes)与有向边(Vertexes)组成,其中节点又分为两类,一类是内部节点,一类是叶子节点。内部节点表示的是样本特征,而叶子节点代表分类。
|
||
|
||
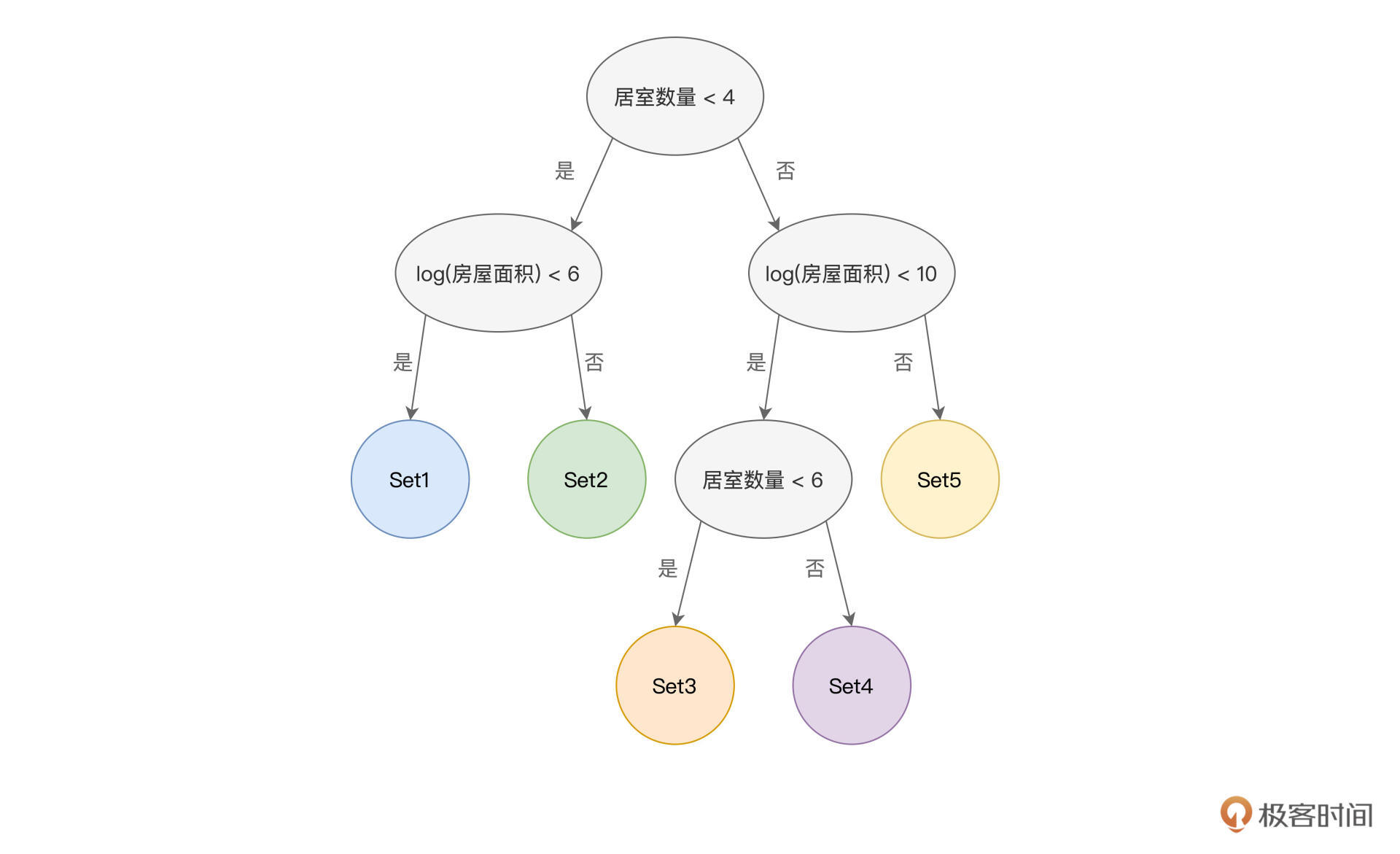
举例来说,假设我们想根据“居室数量”和“房屋面积”这两个特征,把房屋分为5类。那么,我们就可以构建一个决策树,来做到这一点,如下图所示。
|
||
|
||
|
||
|
||
其中,椭圆形代表的是内部节点,每个内部节点都包含一个特征,并同时拥有两条有向边。每条有向边,都表示一组特征取值。比方说,图中决策树的根节点(顶端的内部节点)包含的特征是“居室数量”,左边的有向边,表示的是居室数量小于4的数据样本;而右边的有向边,代表的是居室数量大于等于4的数据样本。
|
||
|
||
就这样,原始的房屋样本被一分为二,按照居室数量被“劈”成了两份。“劈”到左侧的样本,继续按照“房屋面积”是否小于6作区分;而“劈”到右侧的样本,则按照“房屋面积”是否小于10来做进一步的区分。就这样,根据不同特征的不同取值范围,数据样本一层一层地被加以区分,直到圆形节点,也即叶子节点为止。
|
||
|
||
叶子节点表示数据样本的分类,图中的5个圆形即代表5个叶子节点。每个叶子节点中,都包含若干的数据样本,显然,掉落到同一个叶子节点的样本,同属于一个分类。
|
||
|
||
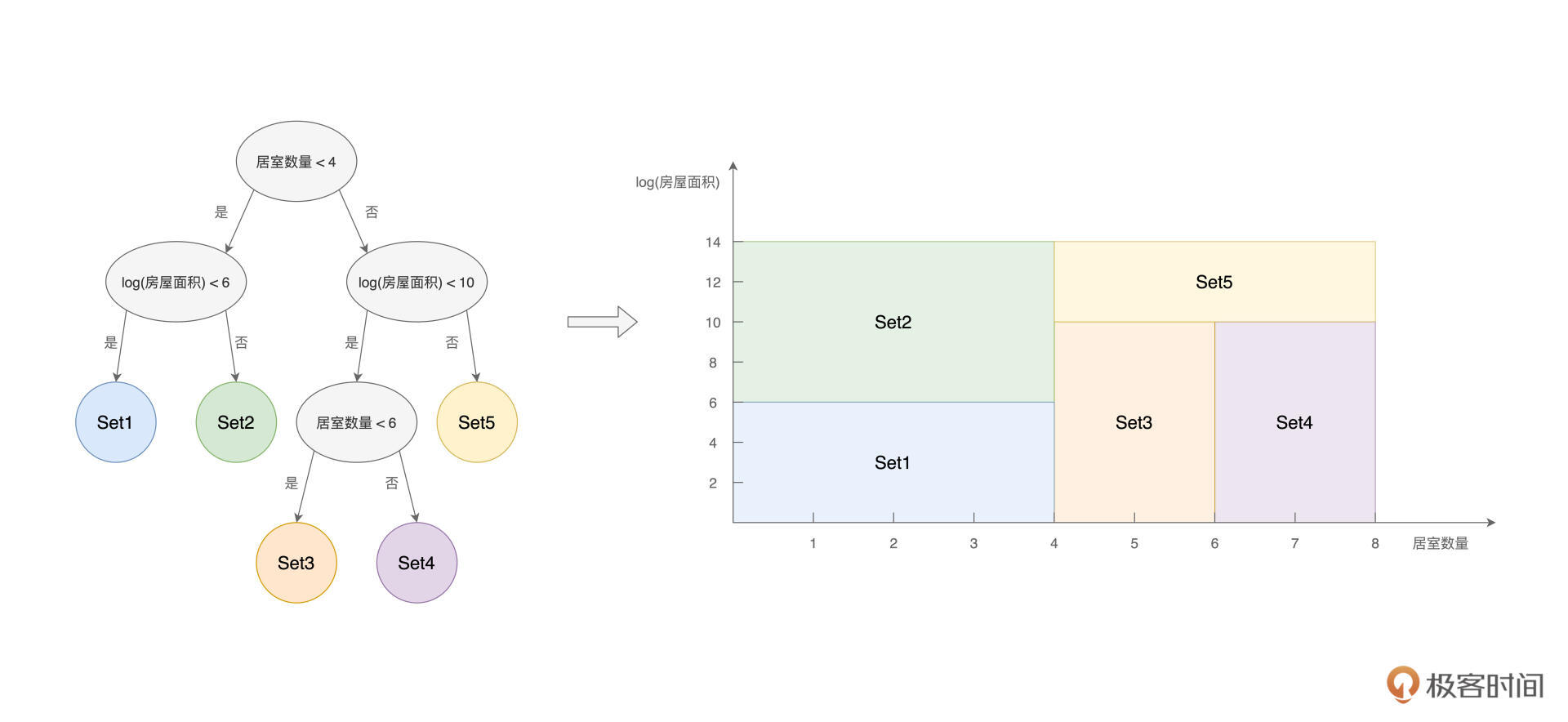
不难发现,在上面的决策树中,结合“居室数量”和“房屋面积”这两个特征的不同取值,原始的数据样本被划分成了“不重不漏”的5份子集,如下图所示。
|
||
|
||
|
||
|
||
基于这5份样本子集,我们就有能力去解决分类或是回归问题。假设数据样本中的标签列(Label)是“房屋质量”,数据样本,按照房屋质量的取值,被分为差、一般、好、很好和极好。
|
||
|
||
决策树中的5个叶子节点,对应的就是Label的5个不同取值。因此,凡是掉落在蓝色圆形节点的样本,它的房屋质量都是“差”,同理,凡是掉落在黄色圆形节点的样本,对应的房屋质量都是“极好”。如此一来,我们便按照“房屋质量”完成了对原始样本的分类过程。
|
||
|
||
实际上,回归过程也是类似的。如果数据样本中的标签不再是离散的“房屋质量”,而是连续的“房屋价格”,那么我们同样可以利用决策树来完成回归预测。假设我们用100条数据样本,来构建上面的决策树,并假设每个叶子节点都包含20条数据样本。
|
||
|
||
那么,当有一条新的数据样本需要预测房价的时候,我们只需要让它遍历决策树,然后看看它掉落到哪一个叶子节点中去。假设它掉落到了Set3这个节点,那么要预测这条样本的房价,我们就取Set3中那20条样本的房价均值。
|
||
|
||
好啦,到此为止,我们介绍了什么是决策树,怎么用决策树来预测新的数据样本。不难发现,**决策树的推理过程,与人类的决策过程非常相似**。
|
||
|
||
人类也常常“货比三家”,结合生活经验,根据一些关键因素做出决策。说到这里,你可能会好奇:“我做决定的时候,往往是结合生活经验,那么模型算法是依据什么,来构建决策树的呢?它怎么知道,哪些特征是决定性因素,而哪些特征又没什么用呢?”
|
||
|
||
用一句话来概括,数据样本的纯度,决定了模型算法选择哪些特征作为内部节点,同时也决定着决策树何时收敛。所谓样本纯度,简单地说,就是标签的多样性(Cardinality)。对于一个集合中的样本,如果样本的标签都一样,也即标签的多样性为1,那么我们就说这个集合的样本纯度很高。
|
||
|
||
相反,如果这个集合中的样本标签取值非常多,多样性非常高,那么我们就说这个集合的样本纯度很低。在数学上,我们可以用信息熵来量化样本的纯度(或者说标签多样性),不过作为入门课,咱们暂时不必深究,只要从概念上理解样本的纯度就好。
|
||
|
||
模型算法在构建决策树的时候,会去遍历每一个特征,并考察每个特征的“提纯”能力。所谓“提纯”,就是把原始样本结合特征进行区分之后,两个样本子集在纯度上有所提升。换句话说,经过候选特征分割后的样本子集,其纯度越高,就代表候选特征的“提纯”能力越高。
|
||
|
||
正是基于这样的逻辑,模型算法依次筛选“提纯”能力最高、次高、第三高的特征,逐级地去构建决策树,直到收敛为止。对于收敛条件,**一方面我们可以人为地设置纯度阈值,另一方面,我们也可以通过设定树的深度(Depth、Levels)来进行限制**。
|
||
|
||
在理想情况下,我们期望决策树每个叶子节点的纯度,尽可能地接近于0(用信息熵来量化),也即每个节点的标签都是一样的。但在实际工作中,我们很难做到这一点。不仅如此,一般来说,一棵决策树的拟合能力是相当有限的,它很难把样本的纯度提升得足够高。
|
||
|
||
这时就要说到GBDT(Gradient-boosted Decision Trees)和RF(Random Forest)这两种算法了,尽管它们的设计思想各不相同,但本质上都是为了进一步提升数据样本的纯度。
|
||
|
||
### Random Forest
|
||
|
||
Random Forest,又叫“随机森林”,它的设计思想是“三个臭皮匠、赛过诸葛亮”。既然一棵树的拟合能力有限,那么就用多棵树来“凑数儿”,毕竟,老话说得好:人多出韩信。
|
||
|
||
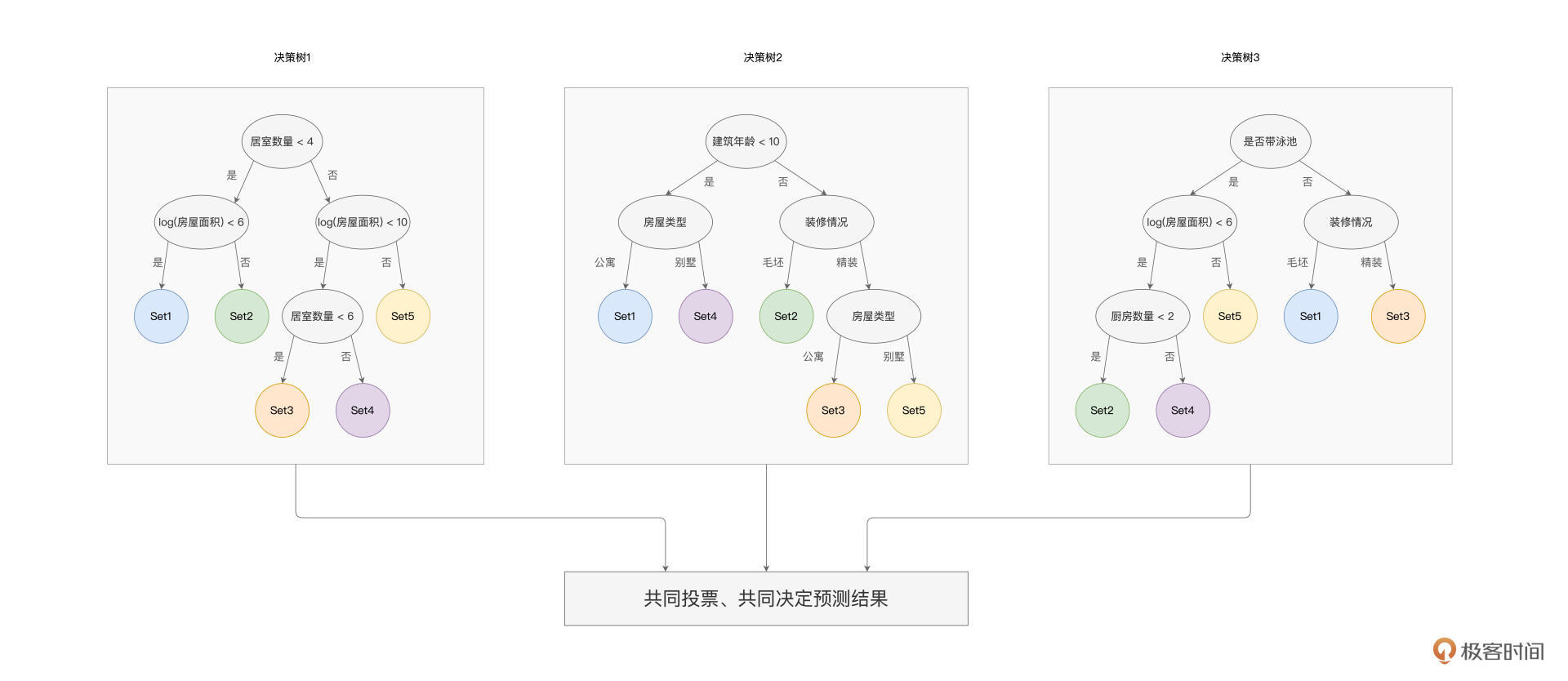
举例来说,我们想结合多个特征,来对房屋质量进行分类。对于给定的数据样本,随机森林算法会训练多棵决策树,树与树之间是相互独立的,彼此之间不存在任何依赖关系。对于每一棵树,算法会随机选择部分样本与部分特征,来进行决策树的构建,这也是随机森林命名中“随机”一词的由来。
|
||
|
||
|
||
|
||
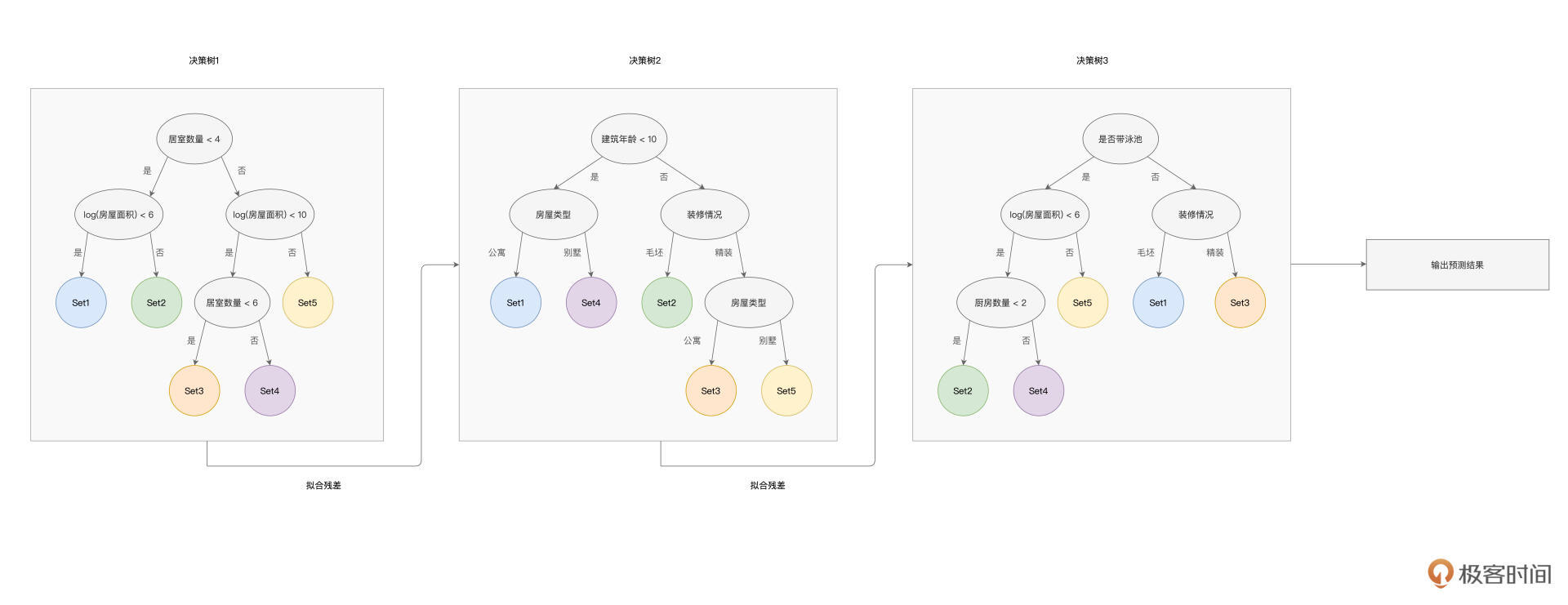
以上图为例,随机森林算法构建了3棵决策树,第一棵用到了“居室数量”和“房屋面积”这两个特征,而第二棵选择了“建筑年龄”、“装修情况”和“房屋类型”三个特征,最后一棵树选择的是“是否带泳池”、“房屋面积”、“装修情况”和“厨房数量”四个特征。
|
||
|
||
每棵树都把遍历的样本分为5个类别,每个类别都包含部分样本。当有新的数据样本需要预测房屋质量时,我们把数据样本同时“喂给”随机森林的3棵树,预测结果取决于3棵树各自的输出结果。
|
||
|
||
假设样本经过第一棵树的判别之后,掉落在了Set3;经过第二棵树的“决策”之后,掉落在了Set2;而经过第三棵树的判定之后,归类到了Set3,那么样本最终的预测结果就是Set3。也即按照“少数服从多数”的原则,随机森林最终的预测结果,会取所有决策树结果中的大多数。回归问题也是类似,最简单的办法,就是取所有决策树判定结果的均值。
|
||
|
||
### GBDT
|
||
|
||
接下来,我们再说说GBDT(Gradient-boosted Decision Trees)。与随机森林类似,GBDT也是用多棵决策树来拟合数据样本,但是,树与树之间是有依赖关系的,每一棵树的构建,都是基于前一棵树的训练结果。因此,与随机森林不同,GBDT的设计思想是“站在前人的肩膀上看得更远”,如下图所示。
|
||
|
||
|
||
|
||
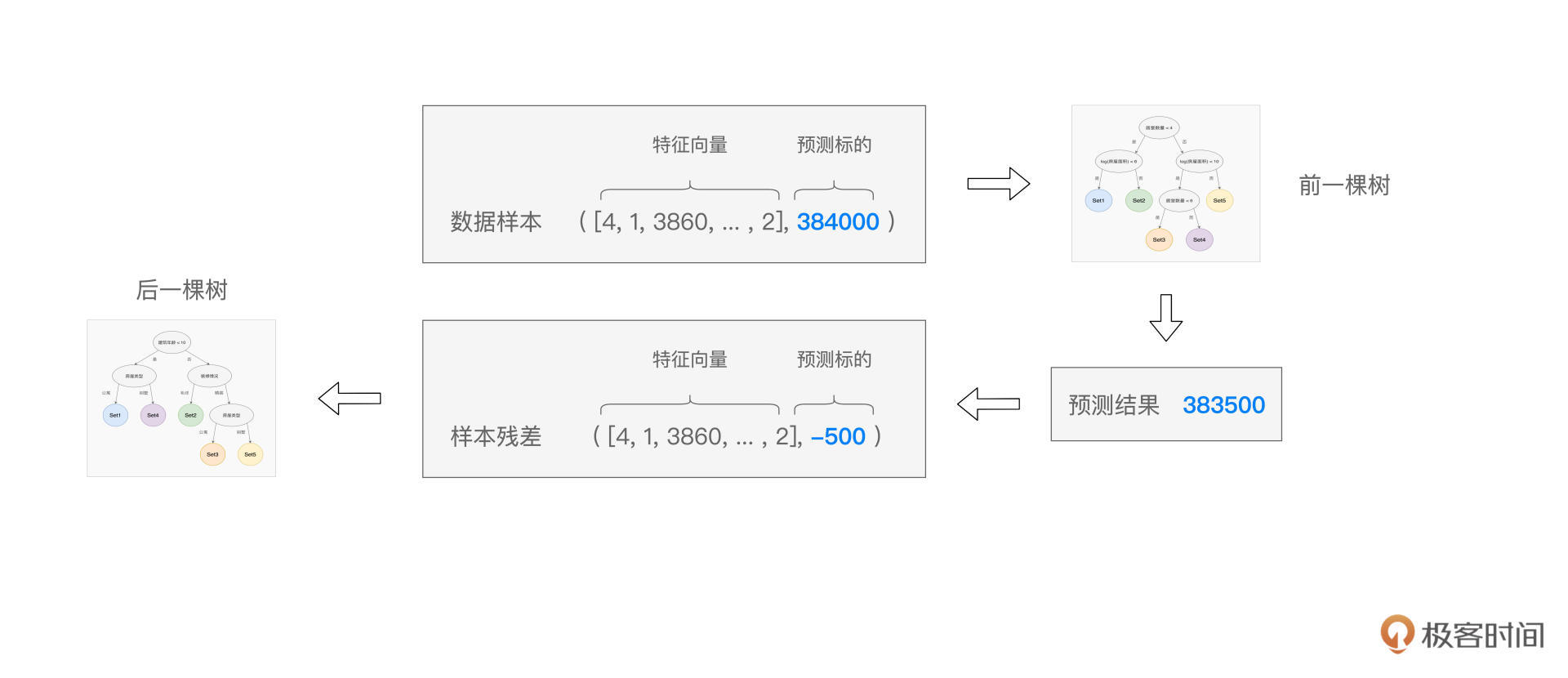
具体来说,在GBDT的训练过程中,每一棵树的构建,都是基于上一棵树输出的“样本残差”。如下图所示,预测值与真实值(Ground Truth)之间的差值,即是样本残差。后面决策树的拟合目标,不再是原始的房屋价格,而是这个样本残差。
|
||
|
||
|
||
|
||
以此类推,后续的决策树,都会基于上一棵树的残差去做拟合,从而使得预测值与真实值之间的误差越来越小,并最终趋近于0。不难发现,只要GBDT训练的决策树足够多,预测误差就可以足够小,因此,GBDT的拟合能力是非常强的。
|
||
|
||
不过,与此同时,我们要提防GBDT的过拟合问题,在训练集上过分拟合,往往会导致模型在测试集上的表现不尽如人意。解决过拟合的思路,就是让模型由复杂变得简单,要做到这一点,我们可以通过限制决策树的数量与深度,来降低GBDT模型的复杂度。
|
||
|
||
好啦,到此为止,我们学习了决策树,以及由决策树衍生的随机森林与GBDT算法。光说不练假把式,在下一讲,我们就以房价预测和房屋分类为例,体会一下在Spark MLlib的框架下,具体要如何应用这些算法解决实际问题。
|
||
|
||
## 重点回顾
|
||
|
||
好啦,到此为止,我们今天的内容就全部讲完啦。让我们一起来做个总结。
|
||
|
||
首先,你需要知道,Spark MLlib开发框架都支持哪些模型算法,我把这些模型算法、以及算法的分类整理到了下面的脑图中,供你随时参考。
|
||
|
||

|
||
|
||
你需要掌握决策树系列算法的特点与基本原理。其中,决策树系列算法,既可以用于解决分类问题,也可以解决回归问题。相比线性模型,树模型拥有更强的非线性拟合能力,而且树模型具备良好的可解释性,它的工作原理非常符合人类的思考方式。随机森林与GBDT,是衍生自决策树的两类集成类算法。
|
||
|
||
随机森林的设计思想是“三个臭皮匠、赛过诸葛亮”,通过在多棵树上随机选取训练样本与特征,随机森林将多个简单模型集成在一起,用投票的方式共同来决定最终的预测结果。
|
||
|
||
而GBDT的思想是“站在前人的肩膀上看得更远”,它也是基于多棵树的集成模型。与随机森林不同,在GBDT中,树与树之间是存在依赖关系的。每一棵树的训练,都是基于前一棵树拟合的样本残差,从而使得预测值不断地逼近真实值。**GBDT的特点是拟合能力超强,但同时要注意决策树过深、过多而带来的过拟合隐患**。
|
||
|
||
## 每课一练
|
||
|
||
结合今天的课程内容,你能说说GBDT与Random Forest模型算法各自的优缺点吗?
|
||
|
||
欢迎你在留言区跟我交流互动,也推荐你把这一讲的内容分享给更多的同事、朋友。
|
||
|