|
|
# 04 | 解线性方程组:为什么用矩阵求解的效率这么高?
|
|
|
|
|
|
你好,我是朱维刚。欢迎你跟我一起重学线性代数!
|
|
|
|
|
|
在上一节课中,我讲解了线性方程组的另一种表达——矩阵。那么今天,我们就来讲解一下如何使用矩阵来解线性方程组,也就是如何求线性方程组的特殊解和通用解。
|
|
|
|
|
|
简单的线性方程组,我们当然可以运用初中学过的知识来求解,那复杂的呢?硬来几乎是不可能的了,一方面是因为人工计算的错误率很高,另一方面,即使我们使用计算机,用类似for或while循环来实现算法,它的计算效率也是极低的。你需要用更科学的方式、方法,从另一个角度来看待和求解线性方程组。
|
|
|
|
|
|
而矩阵就是为我们打开高效之门的钥匙,从计算机科学的角度来说,使用矩阵的运算效率实在是高太多了,因为它可以利用计算机的并行能力,甚至在一些迭代法中,还能实现分布式并行计算(迭代法会在后面“应用篇”中讲解)。
|
|
|
|
|
|
## 线性方程组解的寻找
|
|
|
|
|
|
现在,就让我们开始去寻找线性方程组的解。在之前的课程中,我们已经引入了线性方程组的一般表达,你可以看看下面的例子。
|
|
|
|
|
|
$$
|
|
|
\\left\\{\\begin{array}{l}
|
|
|
a\_{11} x\_{1}+a\_{12} x\_{2}+\\cdots+a\_{1 n} x\_{n}=b\_{1} \\\\\\
|
|
|
a\_{21} x\_{1}+a\_{22} x\_{2}+\\cdots+a\_{2 n} x\_{n}=b\_{2} \\\\\\
|
|
|
\\cdots \\cdots \\cdots \\cdots \\cdots \\cdots \\cdots \\cdots \\cdots \\cdots \\cdots \\\\\\
|
|
|
a\_{m 1} x\_{1}+a\_{m 2} x\_{2}+\\cdots+a\_{m n} x\_{n}=b\_{m}
|
|
|
\\end{array}\\right.
|
|
|
$$
|
|
|
|
|
|
其中,$a\_{ij}$和 $b\_{i}$ 属于实数,而且是已知常数,而$x\_{j}$是未知变量,$i$和$j$的取值范围分别是:$i=1,…,m$;$j=1,…,n$ 。如果我们用矩阵的简单表达方式来看的话,就是$Ax=B$。
|
|
|
|
|
|
要搞清楚概念,我们还是要多看具体的例子。让我们先来看一个实例,来加深一下理解。
|
|
|
|
|
|
$$
|
|
|
\\left\[\\begin{array}{cccc}
|
|
|
1 & 0 & 8 & -4 \\\\\\
|
|
|
0 & 1 & 2 & 12
|
|
|
\\end{array}\\right\]\\left\[\\begin{array}{c}
|
|
|
x\_{1} \\\\\\
|
|
|
x\_{2} \\\\\\
|
|
|
x\_{3} \\\\\\
|
|
|
x\_{4}
|
|
|
\\end{array}\\right\]=\\left\[\\begin{array}{c}
|
|
|
42 \\\\\\
|
|
|
8
|
|
|
\\end{array}\\right\]
|
|
|
$$
|
|
|
|
|
|
很明显,这是一个矩阵表达方式。它的一般线性方程组表达方式是中学的基础知识,你应该很熟悉了。
|
|
|
|
|
|
$$
|
|
|
\\left\\{\\begin{array}{l}
|
|
|
1 \\times x\_{1}+0 \\times x\_{2}+8 \\times x\_{3}+(-4) \\times x\_{4}=42 \\\\\\
|
|
|
0 \\times x\_{1}+1 \\times x\_{2}+2 \\times x\_{3}+12 \\times x\_{4}=8
|
|
|
\\end{array}\\right.
|
|
|
$$
|
|
|
|
|
|
在这个一般线性方程组中,有四个未知变量,但只有两个等式,这就意味着这个线性方程组有无穷多个解(这个是中学数学的范畴)。通过细心观察,我们可以发现第一列和第二列都是由0和1组成的,因此你很容易就能发现其中一个解。
|
|
|
|
|
|
$$
|
|
|
42\\left\[\\begin{array}{l}
|
|
|
1 \\\\\\
|
|
|
0
|
|
|
\\end{array}\\right\]+8\\left\[\\begin{array}{l}
|
|
|
0 \\\\\\
|
|
|
1
|
|
|
\\end{array}\\right\]=\\left\[\\begin{array}{c}
|
|
|
42 \\\\\\
|
|
|
8
|
|
|
\\end{array}\\right\]
|
|
|
$$
|
|
|
|
|
|
这个解就是$\\left\[\\begin{array}{llll}42 & 8 & 0 & 0\\end{array}\\right\]^{T}$,也就是说四个未知变量分别为$42$、$8$、$0$、$0$。
|
|
|
|
|
|
$$
|
|
|
\\left\\{\\begin{array}{l}
|
|
|
x\_{1}=42 \\\\\\
|
|
|
x\_{2}=8 \\\\\\
|
|
|
x\_{3}=0 \\\\\\
|
|
|
x\_{4}=0
|
|
|
\\end{array}\\right.
|
|
|
$$
|
|
|
|
|
|
这个解也叫做特殊解。我们刚才已经说过,这个线性方程组有无穷多个解,那我们确实需要一个聪明的方式来找到其他的解,最直观的方式就是通过矩阵的列来构造0。例如,对于第三列来说,我们可以使用第一和第二列的组合形式来表达。
|
|
|
|
|
|
$$
|
|
|
8\\left\[\\begin{array}{l}
|
|
|
1 \\\\\\
|
|
|
0
|
|
|
\\end{array}\\right\]+2\\left\[\\begin{array}{l}
|
|
|
0 \\\\\\
|
|
|
1
|
|
|
\\end{array}\\right\]=\\left\[\\begin{array}{l}
|
|
|
8 \\\\\\
|
|
|
2
|
|
|
\\end{array}\\right\]
|
|
|
$$
|
|
|
|
|
|
通过计算$Ax=0$,我们得出解$\\left\[\\begin{array}{llll}8 & 2 & -1 & 0\\end{array}\\right\]^{T}$。而事实上,这个解可以乘以任何实数$λ\_{1}$,使得$Ax=0$成立。
|
|
|
|
|
|
$$
|
|
|
\\left\[\\begin{array}{cccc}
|
|
|
1 & 0 & 8 & -4 \\\\\\
|
|
|
0 & 1 & 2 & 12
|
|
|
\\end{array}\\right\]
|
|
|
\\left(\\begin{array}{l}
|
|
|
\\lambda\_{1}\\left\[\\begin{array}{l}
|
|
|
8 \\\\\\
|
|
|
2 \\\\\\
|
|
|
\-1 \\\\\\
|
|
|
0
|
|
|
\\end{array}\\right\]
|
|
|
\\end{array}\\right)=0
|
|
|
$$
|
|
|
|
|
|
同理,对于第四列来说,我们可以使用第一和第二列的组合形式来表达,得出另一套解,使得$Ax=0$。
|
|
|
|
|
|
$$
|
|
|
\\left\[\\begin{array}{cccc}
|
|
|
1 & 0 & 8 & -4 \\\\\\
|
|
|
0 & 1 & 2 & 12
|
|
|
\\end{array}\\right\]
|
|
|
\\left(\\begin{array}{l}
|
|
|
\\lambda\_{2}\\left\[\\begin{array}{l}
|
|
|
\-4 \\\\\\
|
|
|
12 \\\\\\
|
|
|
0 \\\\\\
|
|
|
\-1
|
|
|
\\end{array}\\right\]
|
|
|
\\end{array}\\right)=0
|
|
|
$$
|
|
|
|
|
|
现在,我们可以把之前的特殊解与刚得出的两套解相组合,得出最终解,这个解也就是我们所说的通用解了。
|
|
|
|
|
|
$$
|
|
|
x \\in R^{4}: x=\\left\[\\begin{array}{c}
|
|
|
42 \\\\\\
|
|
|
8 \\\\\\
|
|
|
0 \\\\\\
|
|
|
0
|
|
|
\\end{array}\\right\]+\\lambda\_{1}\\left\[\\begin{array}{c}
|
|
|
8 \\\\\\
|
|
|
2 \\\\\\
|
|
|
\-1 \\\\\\
|
|
|
0
|
|
|
\\end{array}\\right\]+\\lambda\_{2}\\left\[\\begin{array}{c}
|
|
|
\-4 \\\\\\
|
|
|
12 \\\\\\
|
|
|
0 \\\\\\
|
|
|
\-1
|
|
|
\\end{array}\\right\], \\lambda\_{1}, \\lambda\_{2} \\in R
|
|
|
$$
|
|
|
|
|
|
我来总结一下寻找通用解的过程,这个过程分为三步:
|
|
|
|
|
|
1. 我们要寻找一个特殊解,使得$Ax=b$;
|
|
|
2. 找到$Ax=0$的所有解;
|
|
|
3. 组合第一和第二步的解形成通用解。
|
|
|
|
|
|
看到了这里,你有没有发现有些奇怪呢?或者说,有没有觉得哪里有点别扭?是的,好像有点太顺利了。那是因为这个线性方程组比较特别,第一列和第二列是由1和0组成的。所以,我们只通过观察就能得出特殊解和通用解。
|
|
|
|
|
|
然而,你不可能每次都行大运,就像我们在现实中碰到的这类线性方程组,一般都比这个复杂得多。不过不要慌,有一个算法可以来帮助我们转换任意线性方程组,形成类似的特殊形式,这个算法叫做**高斯消元法**。
|
|
|
|
|
|
高斯消元法的核心就是**线性方程组的初等变换**,于是,我们可以通过高斯消元法,得到围绕初等变换形成的简单矩阵表达形式,接下来我们就可以运用之前的三个步骤来寻找通用解了。
|
|
|
|
|
|
## 初等变换的一般形式
|
|
|
|
|
|
既然高斯消元法的核心就是线性方程组的初等变换,那为了方便你使用高斯消元法,我就有必要来讲一讲初等变换的一般形式有哪些:
|
|
|
|
|
|
1. 两个等式的交换,也就是矩阵行交换;
|
|
|
2. 一个等式,或者说矩阵行乘以一个实数常量;
|
|
|
3. 两个等式相加,或者说矩阵的两行相加。
|
|
|
|
|
|
道理是这样的道理,那我们通过一个例子来看看,究竟该怎么做线性方程组的初等变换。假设a属于实数,现在我们试着来寻找下面这个线性方程组的所有解。我把这个过程细细地拆解为11个步骤,建议你仔细看过并理解后,再进入下一阶段的学习。
|
|
|
|
|
|
$$
|
|
|
\\left\\{\\begin{array}{c}
|
|
|
\-2 x\_{1}+4 x\_{2}-2 x\_{3}-x\_{4}+4 x\_{5}=-3 \\\\\\
|
|
|
4 x\_{1}-8 x\_{2}+3 x\_{3}-3 x\_{4}+x\_{5}=2 \\\\\\
|
|
|
x\_{1}-2 x\_{2}+x\_{3}-x\_{4}+x\_{5}=0 \\\\\\
|
|
|
x\_{1}-2 x\_{2}-3 x\_{4}+4 x\_{5}=a
|
|
|
\\end{array}\\right.
|
|
|
$$
|
|
|
|
|
|
1.我们要把这个线性方程组转换成矩阵的表达形式,$Ax=b$。
|
|
|
|
|
|
$$
|
|
|
\\left\[\\begin{array}{ccccccc}
|
|
|
\-2 & 4 & -2 & -1 & 4 & \\mid & -3 \\\\\\
|
|
|
4 & -8 & 3 & -3 & 1 & \\mid & 2 \\\\\\
|
|
|
1 & -2 & 1 & -1 & 1 & \\mid & 0 \\\\\\
|
|
|
1 & -2 & 0 & -3 & 4 & \\mid & a
|
|
|
\\end{array}\\right\]
|
|
|
$$
|
|
|
|
|
|
2.接着我们来交换第一和第三行。
|
|
|
|
|
|
$$
|
|
|
\\left\[\\begin{array}{ccccccc}
|
|
|
1 & -2 & 1 & -1 & 1 & \\mid & 0 \\\\\\
|
|
|
4 & -8 & 3 & -3 & 1 & \\mid & 2 \\\\\\
|
|
|
\-2 & 4 & -2 & -1 & 4 & \\mid & -3 \\\\\\
|
|
|
1 & -2 & 0 & -3 & 4 & \\mid & a
|
|
|
\\end{array}\\right\]
|
|
|
$$
|
|
|
|
|
|
注意,你知道我们为什么选择第一行和第三行交换吗?其实,这是为了便于计算。而具体交换哪一行是有个小技巧的,如果某行的第一个元素有1,我们就可以把这一行移到第一行。
|
|
|
|
|
|
3.我们以第一行为基础,开始执行乘和加变换,将第一行乘以-4的结果和第二行相加,从而获得了下面这样的结果。
|
|
|
|
|
|
$$
|
|
|
\\left\[\\begin{array}{ccccccc}
|
|
|
1 & -2 & 1 & -1 & 1 & \\mid & 0 \\\\\\
|
|
|
0 & 0 & -1 & 1 & -3 & \\mid & 2 \\\\\\
|
|
|
\-2 & 4 & -2 & -1 & 4 & \\mid & -3 \\\\\\
|
|
|
1 & -2 & 0 & -3 & 4 & \\mid & a
|
|
|
\\end{array}\\right\]
|
|
|
$$
|
|
|
|
|
|
4.然后,我们用同样的方法,将第一行乘以2的结果,再和第三行相加,得到了下面这样的结果。
|
|
|
|
|
|
$$
|
|
|
\\left\[\\begin{array}{ccccccc}
|
|
|
1 & -2 & 1 & -1 & 1 & \\mid & 0 \\\\\\
|
|
|
0 & 0 & -1 & 1 & -3 & \\mid & 2 \\\\\\
|
|
|
0 & 0 & 0 & -3 & 6 & \\mid & -3 \\\\\\
|
|
|
1 & -2 & 0 & -3 & 4 & \\mid & a
|
|
|
\\end{array}\\right\]
|
|
|
$$
|
|
|
|
|
|
5.以此类推,我们将第一行乘以-1的结果,和第四行相加,继续获得新矩阵。
|
|
|
|
|
|
$$
|
|
|
\\left\[\\begin{array}{ccccccc}
|
|
|
1 & -2 & 1 & -1 & 1 & \\mid & 0 \\\\\\
|
|
|
0 & 0 & -1 & 1 & -3 & \\mid & 2 \\\\\\
|
|
|
0 & 0 & 0 & -3 & 6 & \\mid & -3 \\\\\\
|
|
|
0 & 0 & -1 & -2 & 3 & \\mid & a
|
|
|
\\end{array}\\right\]
|
|
|
$$
|
|
|
|
|
|
6.将第二行乘以-1的结果,和第四行相加,得到下面这样的结果。
|
|
|
|
|
|
$$
|
|
|
\\left\[\\begin{array}{ccccccc}
|
|
|
1 & -2 & 1 & -1 & 1 & \\mid & 0 \\\\\\
|
|
|
0 & 0 & -1 & 1 & -3 & \\mid & 2 \\\\\\
|
|
|
0 & 0 & 0 & -3 & 6 & \\mid & -3 \\\\\\
|
|
|
0 & 0 & 0 & -3 & 6 & \\mid & a-2
|
|
|
\\end{array}\\right\]
|
|
|
$$
|
|
|
|
|
|
7.将第三行乘以-1的结果,和第四行相加。
|
|
|
$$
|
|
|
\\left\[\\begin{array}{ccccccc}
|
|
|
1 & -2 & 1 & -1 & 1 & \\mid & 0 \\\\\\
|
|
|
0 & 0 & -1 & 1 & -3 & \\mid & 2 \\\\\\
|
|
|
0 & 0 & 0 & -3 & 6 & \\mid & -3 \\\\\\
|
|
|
0 & 0 & 0 & 0 & 0 & \\mid & a+1
|
|
|
\\end{array}\\right\]
|
|
|
$$
|
|
|
|
|
|
8.第二行乘以-1,第三行乘以$-\\frac{1}{3}$。
|
|
|
$$
|
|
|
\\left\[\\begin{array}{ccccccc}
|
|
|
1 & -2 & 1 & -1 & 1 & \\mid & 0 \\\\\\
|
|
|
0 & 0 & 1 & -1 & 3 & \\mid & -2 \\\\\\
|
|
|
0 & 0 & 0 & 1 & -2 & \\mid & 1 \\\\\\
|
|
|
0 & 0 & 0 & 0 & 0 & \\mid & a+1
|
|
|
\\end{array}\\right\]
|
|
|
$$
|
|
|
|
|
|
9.现在,这个矩阵就是一个简单形式的矩阵,也叫做**行阶梯形矩阵**(Row-Echelon Form,REF)。
|
|
|
|
|
|
$$
|
|
|
\\left\\{\\begin{array}{r}
|
|
|
x\_{1}-2 x\_{2}+x\_{3}-x\_{4}+x\_{5}=0 \\\\\\
|
|
|
x\_{3}-x\_{4}+3 x\_{5}=-2 \\\\\\
|
|
|
x\_{4}-2 x\_{5}=1 \\\\\\
|
|
|
0=a+1
|
|
|
\\end{array}\\right.
|
|
|
$$
|
|
|
|
|
|
一个矩阵成为行阶梯形矩阵需满足两个条件:
|
|
|
|
|
|
* 如果它既有零行,又有非零行,则零行在下,非零行在上;
|
|
|
* 如果它有非零行,则每个非零行的第一个非零元素所在列号自上而下严格单调上升,正如之前的这个矩阵,列号自上而下是1、3、4,是严格单调上升的。
|
|
|
|
|
|
10.你可以看出,只有在$a=-1$的情况下,这个线性方程组才有解,特殊解是$\\left\[\\begin{array}{lllll}2 & 0 & -1 & 1 & 0\\end{array}\\right\]^{\\mathrm{T}}$。
|
|
|
|
|
|
11.最后,我们得出这个线性方程组的通用解,如下图所示。
|
|
|
|
|
|
$$
|
|
|
x \\in R^{5}: x=\\left\[\\begin{array}{c}
|
|
|
2 \\\\\\
|
|
|
0 \\\\\\
|
|
|
\-1 \\\\\\
|
|
|
1 \\\\\\
|
|
|
0
|
|
|
\\end{array}\\right\]+\\lambda\_{1}\\left\[\\begin{array}{l}
|
|
|
2 \\\\\\
|
|
|
1 \\\\\\
|
|
|
0 \\\\\\
|
|
|
0 \\\\\\
|
|
|
0
|
|
|
\\end{array}\\right\]+\\lambda\_{2}\\left\[\\begin{array}{c}
|
|
|
2 \\\\\\
|
|
|
0 \\\\\\
|
|
|
\-1 \\\\\\
|
|
|
2 \\\\\\
|
|
|
1
|
|
|
\\end{array}\\right\], \\lambda\_{1}, \\lambda\_{2} \\in R
|
|
|
$$
|
|
|
|
|
|
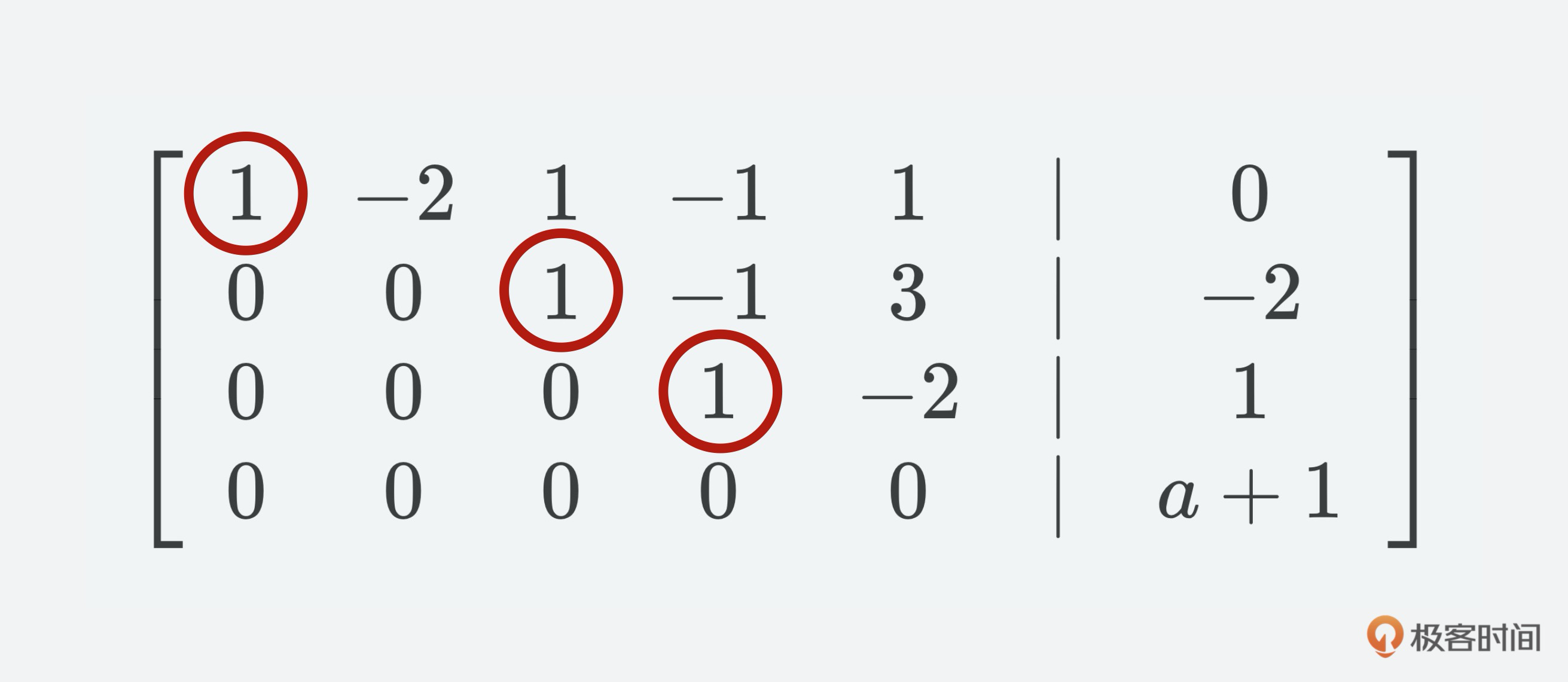
注意,这里有一个概念很重要,那就是**主元**。主元就是在矩阵消元过程中,每列要保留的非零元素,我们可以用它把该列其他元素消去。在阶梯型矩阵中,每个非零行第一个非零元素就是主元。
|
|
|
|
|
|
拿之前的第8步计算后的结果来举例,第一行的第一个元素1就是主元,第二行第三个元素1是主元,第三行的第四个元素1也是主元。
|
|
|
|
|
|
|
|
|
|
|
|
对应行阶梯形矩阵主元的变量叫做基本变量,而其他的变量叫做自由变量,这个例子中,$x\_{1}$、$x\_{3}$、$x\_{4}$就是基本变量,$x\_{2}$、$x\_{5}$则是自由变量。使用行阶梯形矩阵能更简单地得出特殊解,所以我们可以使用主元列来表达线性方程组:
|
|
|
|
|
|
$$
|
|
|
b=\\sum\_{i=1}^{P} \\lambda\_{i} \\mathrm{p}\_{i}, i=1, \\ldots, P
|
|
|
$$
|
|
|
|
|
|
在之前的例子中,我们使用主元列来表达成下面这样的矩阵形式:
|
|
|
|
|
|
$$
|
|
|
\\lambda\_{1}\\left\[\\begin{array}{l}
|
|
|
1 \\\\\\
|
|
|
0 \\\\\\
|
|
|
0 \\\\\\
|
|
|
0
|
|
|
\\end{array}\\right\]+\\lambda\_{2}\\left\[\\begin{array}{l}
|
|
|
1 \\\\\\
|
|
|
1 \\\\\\
|
|
|
0 \\\\\\
|
|
|
0
|
|
|
\\end{array}\\right\]+\\lambda\_{3}\\left\[\\begin{array}{c}
|
|
|
\-1 \\\\\\
|
|
|
\-1 \\\\\\
|
|
|
1 \\\\\\
|
|
|
0
|
|
|
\\end{array}\\right\]=\\left\[\\begin{array}{c}
|
|
|
0 \\\\\\
|
|
|
\-2 \\\\\\
|
|
|
1 \\\\\\
|
|
|
0
|
|
|
\\end{array}\\right\]
|
|
|
$$
|
|
|
|
|
|
于是,我们最终得出 $λ\_{3}=1$,$λ\_{2}=-1$,$λ\_{1}=2$ ,分别对应于$x\_{4}$、$x\_{3}$、$x\_{1}$。不要忘了,对于非主元列,我们已经隐式地把系数设置成了$0$,所以这个线性方程组的特殊解是$x=\\left\[\\begin{array}{lllll}2 & 0 & -1 & 1 & 0\\end{array}\\right\]^{\\mathrm{T}}$。
|
|
|
|
|
|
## 简化行阶梯形矩阵
|
|
|
|
|
|
这里我们再引入一个概念,简化行阶梯形矩阵,因为引入简化行阶梯形矩阵对于线性方程组的求解来说会更简单。其实,高斯消元法的核心就是通过初等变换,把线性方程组转换成简化行阶梯形矩阵。那么一个方程组是简化行阶梯形矩阵,必须满足哪几个条件呢?
|
|
|
|
|
|
1. 这个方程组必须是行阶梯形矩阵;
|
|
|
2. 方程组的每一个主元都是1;
|
|
|
3. 主元在它的列中是唯一的非0元素。
|
|
|
|
|
|
现在,我们再通过一个实例,看看该如何通过高斯消元法计算一个矩阵的逆矩阵。设矩阵$A$如下图:
|
|
|
|
|
|
$$
|
|
|
A=\\left\[\\begin{array}{llll}
|
|
|
1 & 0 & 2 & 0 \\\\\\
|
|
|
1 & 1 & 0 & 0 \\\\\\
|
|
|
1 & 2 & 0 & 1 \\\\\\
|
|
|
1 & 1 & 1 & 1
|
|
|
\\end{array}\\right\]
|
|
|
$$
|
|
|
|
|
|
首先,我们形成$A$的增广矩阵(具体方法参见上一节)。
|
|
|
$$
|
|
|
\\left\[\\begin{array}{lllllllll}
|
|
|
1 & 0 & 2 & 0 & \\mid & 1 & 0 & 0 & 0 \\\\\\
|
|
|
1 & 1 & 0 & 0 & \\mid & 0 & 1 & 0 & 0 \\\\\\
|
|
|
1 & 2 & 0 & 1 & \\mid & 0 & 0 & 1 & 0 \\\\\\
|
|
|
1 & 1 & 1 & 1 & \\mid & 0 & 0 & 0 & 1
|
|
|
\\end{array}\\right\]
|
|
|
$$
|
|
|
|
|
|
其次,使用我们前面刚刚讲过的高斯消元法计算出简化行阶梯形矩阵。
|
|
|
|
|
|
$$
|
|
|
\\left\[\\begin{array}{ccccccccc}
|
|
|
1 & 0 & 0 & 0 & \\mid & -1 & 2 & -2 & 2 \\\\\\
|
|
|
0 & 1 & 0 & 0 & \\mid & 1 & -1 & 2 & -2 \\\\\\
|
|
|
0 & 0 & 1 & 0 & \\mid & 1 & -1 & 1 & -1 \\\\\\
|
|
|
0 & 0 & 0 & 1 & \\mid & -1 & 0 & -1 & 2
|
|
|
\\end{array}\\right\]
|
|
|
$$
|
|
|
|
|
|
最后,我们就得到$A$的逆矩阵,如下图所示。
|
|
|
|
|
|
$$
|
|
|
A^{-1}=\\left\[\\begin{array}{cccc}
|
|
|
\-1 & 2 & -2 & 2 \\\\\\
|
|
|
1 & -1 & 2 & -2 \\\\\\
|
|
|
1 & -1 & 1 & -1 \\\\\\
|
|
|
\-1 & 0 & -1 & 2
|
|
|
\\end{array}\\right\]
|
|
|
$$
|
|
|
|
|
|
接下来,我们只要使用公式$A A^{-1}=I$ 就可以对结果进行验证了。
|
|
|
|
|
|
## 更多解线性方程组的方法
|
|
|
|
|
|
到目前为止,相信你已经了解了如何解线性方程组,包括特殊解和通用解,以及如何使用高斯消元法来解线性方程组。最后,我再总结一些解方法来作为你的知识扩展。
|
|
|
|
|
|
第一个方法,假设一个矩阵A是方阵(行数与列数相等的矩阵),并且可逆,$Ax=B$ ,那$x$解就可以写成$x=A^{-1}B$,但如果$A$矩阵不可逆,也不是方阵,那我们就只能使用下面这个变换来求$x$解了。
|
|
|
|
|
|
$$Ax=B⇔A^{T}Ax=A^{T}B⇔x=(A^{T}A)^{-1}A^{T}B$$
|
|
|
|
|
|
其中,矩阵A的转置矩阵和A相乘的逆矩阵,再和A的转置矩阵相乘,我们把它叫做穆尔彭罗斯伪逆矩阵(Moore-Penrose pseudo inverse),简称伪逆。
|
|
|
|
|
|
$$(A^{T}A)^{-1}A^{T}$$
|
|
|
|
|
|
这个方法有两个弊端:第一,矩阵乘和逆矩阵的计算太复杂;第二,数值精确度不高。因此,从实践角度来说,我一般不推荐使用。
|
|
|
|
|
|
第二个方法是高斯消元法。高斯消元法是非常直观的,它在很多计算中都起到了关键的作用,比如:
|
|
|
|
|
|
1. 计算行列式;
|
|
|
2. 检查向量是否是线性独立的;
|
|
|
3. 计算矩阵的逆矩阵;
|
|
|
4. 计算矩阵的秩;
|
|
|
5. 决定向量空间的基。
|
|
|
|
|
|
但当高斯消元法面对百万、千万级别的变量时,就捉襟见肘了。而这类级别的计算才是我们在实践中经常会遇到的,因此从实践角度来说,我也一般不推荐使用。因为高斯消元法属于直接法,直接法是经历有限次的运算得到方程组精确解的方法。但是,学习直接法是有意义的,虽然直接法在实际工作中不常用,但是它也能处理一些日常小问题,更重要的是,它稳固了我们进一步学习其它方法的基础。
|
|
|
|
|
|
我要讲的第三种方法,就是与直接法对应的间接法了。在实践中,线性方程组的求解都是间接的,也就是运用迭代法。
|
|
|
|
|
|
迭代法是采用极限过程,用线性方程组的近似解逐步逼近精确解的方法。所以,迭代法的关键在于每次迭代残余错误的减少,以及如何能够收敛到解。常见的迭代法有两类,定常迭代法(Stationary iterative method)和Krylov子空间方法(我会在应用篇中讲解)。
|
|
|
|
|
|
> 定常迭代法:理查德森迭代法(Richardson method)、雅可比方法(Jacobi method)、Gauß-Seidel方法、逐次超松弛法(Successive over-relaxation method,简称SOR)。
|
|
|
> Krylov子空间方法:共轭梯度法(Conjugate gradient)、 广义极小残余算法(Generalized minimal residual)、双共轭梯度法(Biconjugate gradient)。
|
|
|
|
|
|
这里提到的几种迭代法都是在实践中比较常用的,也是计算机编程中经常实现的算法,但由于迭代法更多属于微分和极限领域,所以这里就不详细介绍了,我会在线性代数应用篇的“数值线性代数”那节课中再做讲解。
|
|
|
|
|
|
如果在课程内容结束后,你还有余力学习更多的内容,这里我先推荐两本书给你作参考,一本是《Introduction to Numerical Analysis》,另一本是《Linear Algebra》。这两本书里面都有进一步地讲解了线性方程组的迭代法求解的内容。
|
|
|
|
|
|
> 1.《Introduction to Numerical Analysis》
|
|
|
> 作者:Stoer, Josef, Bulirsch, R.
|
|
|
> 2002年出版
|
|
|
> 2.《Linear Algebra》
|
|
|
> 作者:Liesen, Jörg, Mehrmann, Volker
|
|
|
> 2015年出版
|
|
|
|
|
|
## 本节小结
|
|
|
|
|
|
好了,到这里解线性方程组这一讲就结束了,最后我再总结一下前面讲解的内容。
|
|
|
|
|
|
首先,我用一个简单的线性方程组,通过直接观察的方法来计算这个方程组的特殊解和通用解,接着通过实例详细地介绍了高斯消元法,最后我给出了一些在实践中常用的线性方程组解方法。只有弄清楚这些基础知识的本质,你才能更进一步,去了解其他计算方法。
|
|
|
|
|
|
线性方程组的求解已经成为了世界上最快计算机的测试标准,因为通过矩阵运算,计算机的并行计算能力暴露无遗。希望你能够在这些基础之上,阅读我推荐的两本书,并且把这些方法运用到实践中,特别是机器学习,因为机器学习也用到了很多迭代方法。
|
|
|
|
|
|
|
|
|
|
|
|
## 线性代数练习场
|
|
|
|
|
|
练习时刻到了,今天的练习题比较简单,请你用高斯消元法求下面的线性方程组。
|
|
|
|
|
|
$$
|
|
|
\\left\\{\\begin{array}{c}
|
|
|
x\_{1}+x\_{2}-2 x\_{3}-x\_{4}=-1 \\\\\\
|
|
|
x\_{1}+5 x\_{2}-3 x\_{3}-2 x\_{4}=0 \\\\\\
|
|
|
3 x\_{1}-x\_{2}+x\_{3}+4 x\_{4}=2 \\\\\\
|
|
|
\-2 x\_{1}+2 x\_{2}+x\_{3}-x\_{4}=1
|
|
|
\\end{array}\\right.
|
|
|
$$
|
|
|
|
|
|
欢迎在留言区和[部落](https://horde.geekbang.org/channel/list/39)里晒出你的运算过程和结果,留下你的学习痕迹。如果你有所收获,也欢迎你把这篇文章分享给你的朋友。
|
|
|
|