You cannot select more than 25 topics
Topics must start with a letter or number, can include dashes ('-') and can be up to 35 characters long.
16 KiB
16 KiB
02 | 基本概念:线性代数研究的到底是什么问题?
你好,我是朱维刚。欢迎你跟我学习线性代数。今天我们要讲的是“线性代数这门课的基本概念”。
线性代数可以运用在很多领域,比如:工程学、计算机科学、经济学、信号处理等等。我们来看一个在经济学中常见的例子:消费矩阵。
假设有n个行业,比如:化学、食品和石油。制造一单位的某化学品需要0.2单位的另一类化学品,0.3单位的食品,以及0.4单位的石油,而制造一单位的某食品和某石油也同样分别需要这三类产品的输入,于是,我们就能构造这样一个消费矩阵:
\\left|\\begin{array}{l}
化学输出 \\\\\\
食品输出 \\\\\\
石油输出
\\end{array}\\right|=\\left\[\\begin{array}{lll}
0.2 & 0.3 & 0.4 \\\\\\
0.4 & 0.4 & 0.1 \\\\\\
0.5 & 0.1 & 0.3
\\end{array}\\right\]\\left|\\begin{array}{l}
化学输入 \\\\\\
食品输入 \\\\\\
石油输入
\\end{array}\\right|$$
当然,我们也可以用一般的线性方程组$Ax=b$的形式来表达:
$$\\left\\{\\begin{array}{l}
0.2 x\_{1}+0.3 x\_{2}+0.4 x\_{3}=b\_{1} \\\\\\
0.4 x\_{1}+0.4 x\_{2}+0.1 x\_{3}=b\_{2} \\\\\\
0.5 x\_{1}+0.1 x\_{2}+0.3 x\_{3}=b\_{3}
\\end{array}\\right.$$
从本质上来说,消费矩阵解决的是输入和输出之间的关系。不仅如此,线性代数在现实生活中的运用还有很多,比如,我们可以借用特征值和特征向量,预测若干年后的污水水平;在密码学中,可以使用矩阵及其逆矩阵对需发送的消息加密;在机器学习中,可以使用线性方程组的共轭迭代法来训练神经网络,等等。
刚才我分别用矩阵和线性方程组的形式给出了消费矩阵,当然,在实际生活中,你可以灵活选择最有效的方式来解决问题。
我们可以看到,线性方程组可以表示成一般形式,也就是你初中学到的$A x=b$的形式,也可以表示成矩阵形式。矩阵是由向量组合而成的,比如刚才例子中的系数矩阵的每一行都是一个**行向量**,每一列都是一个**列向量**。
$$\\begin{array}{l}
\\end{array}\\left\[\\begin{array}{lll}
0.2 & 0.3 & 0.4 \\\\\\
0.4 & 0.4 & 0.1 \\\\\\
0.5 & 0.1 & 0.3
\\end{array}\\right\] \\begin{array}{l}
\\end{array}$$
从这里我们能看出,**向量**其实就会是线性代数最基础的核心。数学对抽象思维要求很高,简单来说,抽象思维就是抽取同类事物的共性。所以,在进入具体的线性方程组的主题前,我要先从数学抽象的角度说一说代数和线性代数,这也是深入理解后面内容的前提。
## 代数和线性代数的基本概念
那什么是代数呢?百度百科的解释是这样的:
> 代数是研究数、数量、关系、结构与代数方程(组)的通用解法及其性质的数学分支。
但我觉得这个解释其实没有说出**代数**这个概念的重点。我的理解是这样的:**代数是构造一系列对象和一系列操作这些对象的规则。**
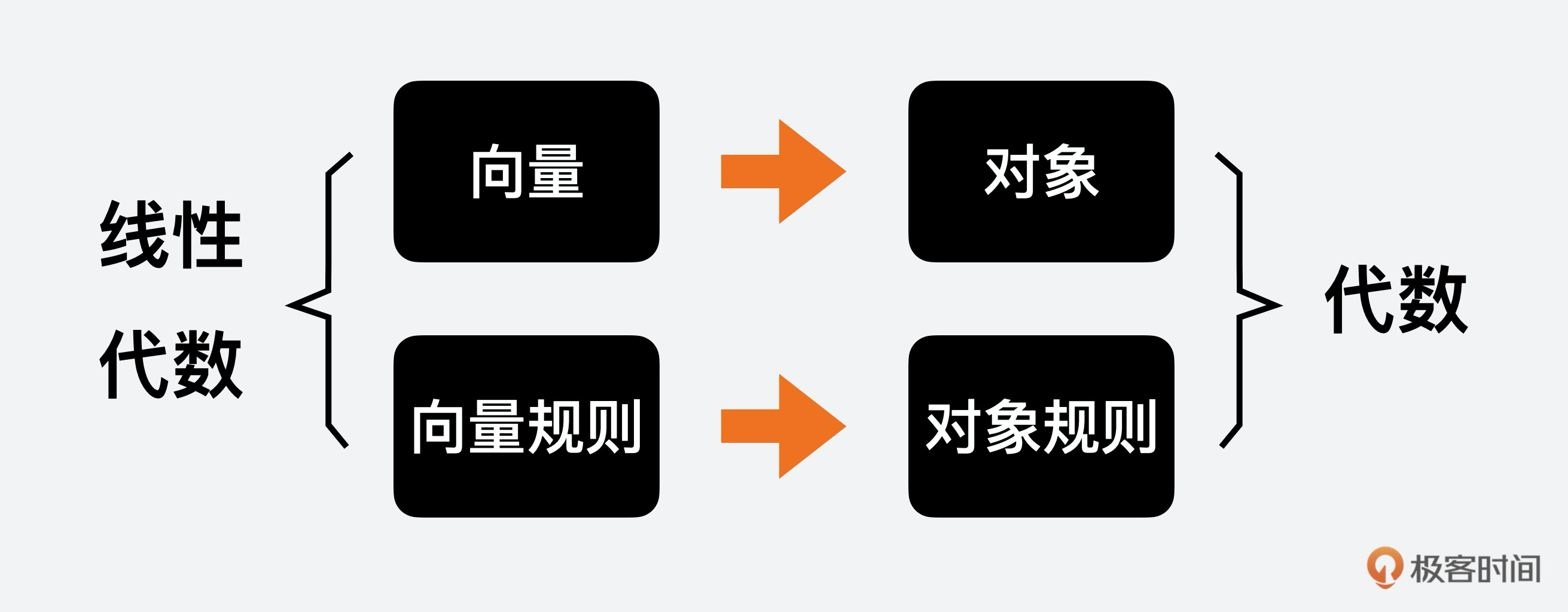
所以你看,代数这个概念的核心就两点,**对象**和**操作对象的规则**,这样就很好理解了吧?那有了代数的定义,线性代数就很好定义了。我们类比来看,线性代数其实就是向量,以及操作这些向量的规则。这里,向量映射到对象,向量的规则映射到对象的规则,因此线性代数是代数的具像化表达。
## 向量的基本概念
那什么是**向量**呢?从样子来看,向量其实就是由字母加上它上面的箭头来表示的,比如我们一版会写成$\\vec{x}$。我估计你在高中或大学里已经接触过“几何向量”。那么,下面我用更抽象的数学观点来给你解释一下。
**向量**,也叫欧几里得向量(Euclidean Vector),其实就是能够互相相加、被标量乘的特殊对象。而标量也叫“无向量”,它只有数值大小,没有方向。怎么理解呢?我们来看一些向量的例子,通过这些例子来深入理解向量的概念。
**几何向量**是有向线段,在二维空间(也就是平面)中,两个几何向量能够相加,比如,向量$x$加上向量$y$等于向量$z$,$\\vec{x}+\\vec{y}=\\vec{z}$ ,$x$向量也能被一个标量乘。再比如,标量$\\lambda$乘向量$x$结果也是向量,$\\lambda \\vec{x}, \\lambda \\in R$。几何向量通过大小和方向来简化向量的表达,所以,一般数学课程一开始都会拿几何向量来进行举例。
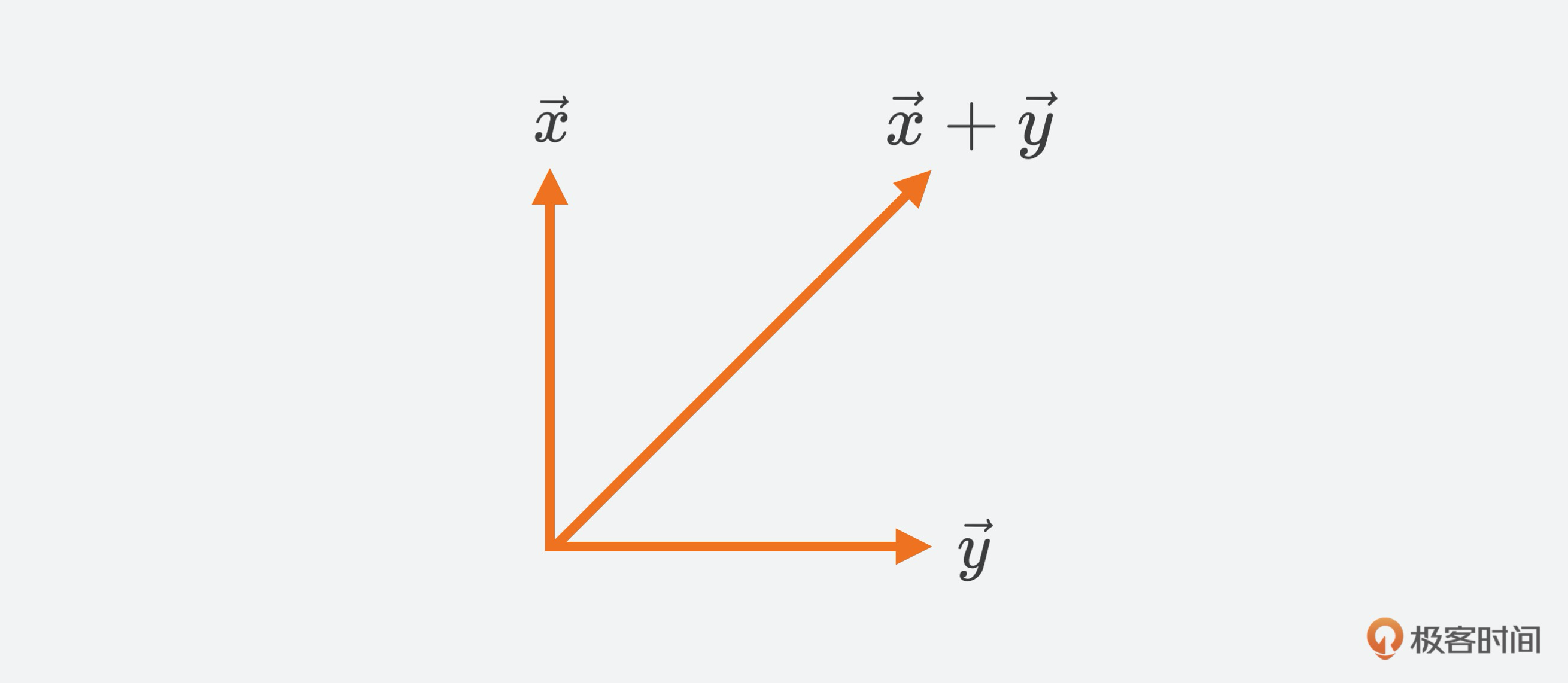
**多项式其实也是向量**。两个多项式能够相加,它也能够被标量乘,结果也是多项式。
**矩阵的一行或一列也是向量。**就比如下面这样形式的向量。
$$x \\in R^{3}: x=\\left\[\\begin{array}{l}
1 \\\\\\
2 \\\\\\
3
\\end{array}\\right\]$$
两个向量能够相加,它也能够被标量乘,结果也是向量。它和现代大部分的编程语言中的数组一致,而且数组的运算简化了向量操作的算法实施。
**矢量图、音频信号也是向量**。它们都能被一系列数字表示,比如,在音频信号处理中,常用到数据增强的方法,通过向量的操作就能到达目标。
看了这些向量例子,不知道你现在有点感觉了吗?其实,线性代数的本质就是**寻找向量之间的相似性**,比如在做分类时,我们常常需要估算不同样本之间的相似性度量(Similarity Measurement),这时通常采用的方法就是计算样本间的“距离”(Distance)。
可以看出来,向量非常重要,我们后面很多内容都是从向量延伸而来的,比如矩阵和求解线性方程组。
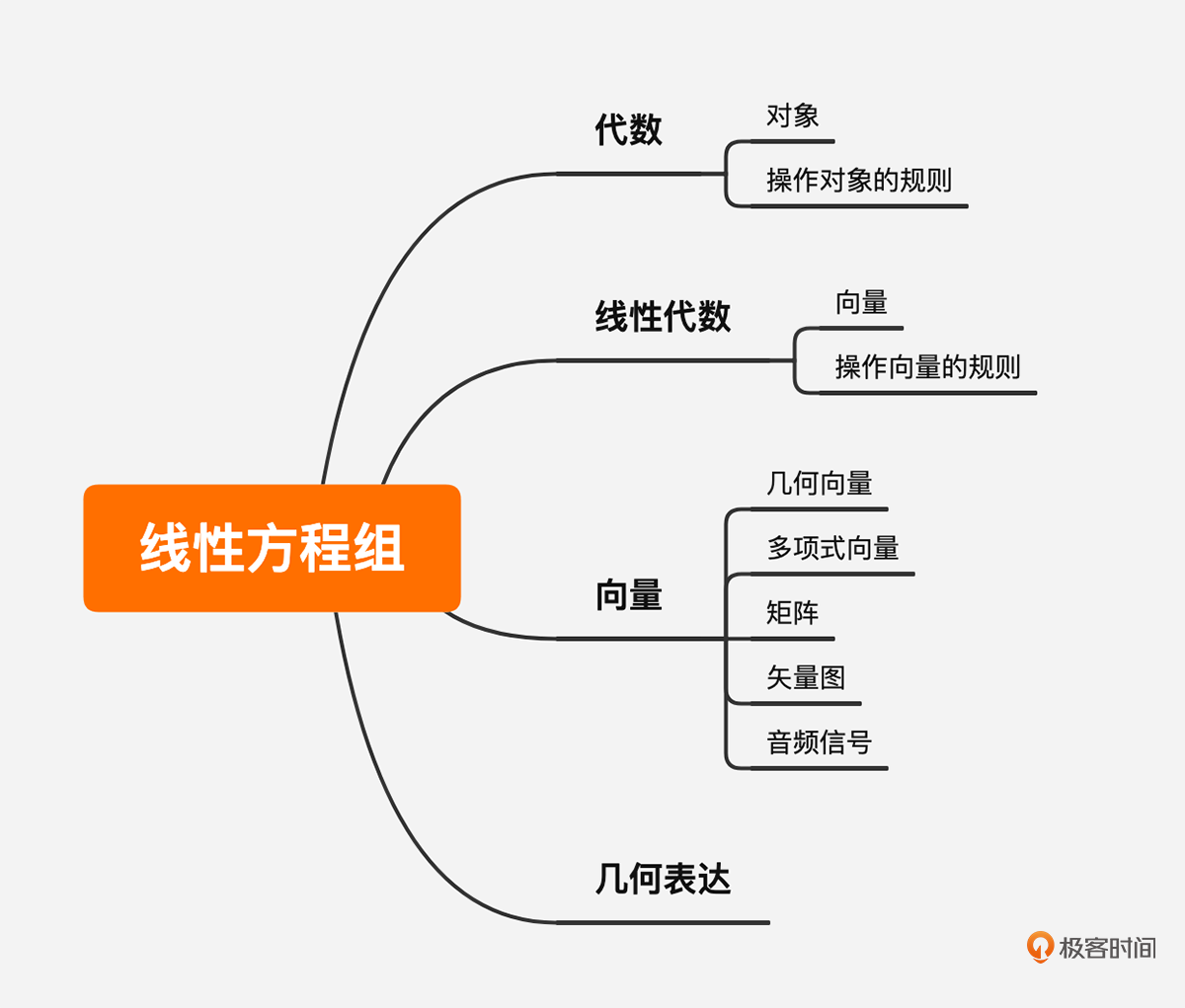
下面我用一张图来表达和向量有关的所有概念,也就是线性代数所有的核心内容,其中大部分内容你都会学到,希望通过这个图,你对线性代数有个大概的认知。相信学习完所有课程后,你再回过头来看时,肯定会有一些新的认知。
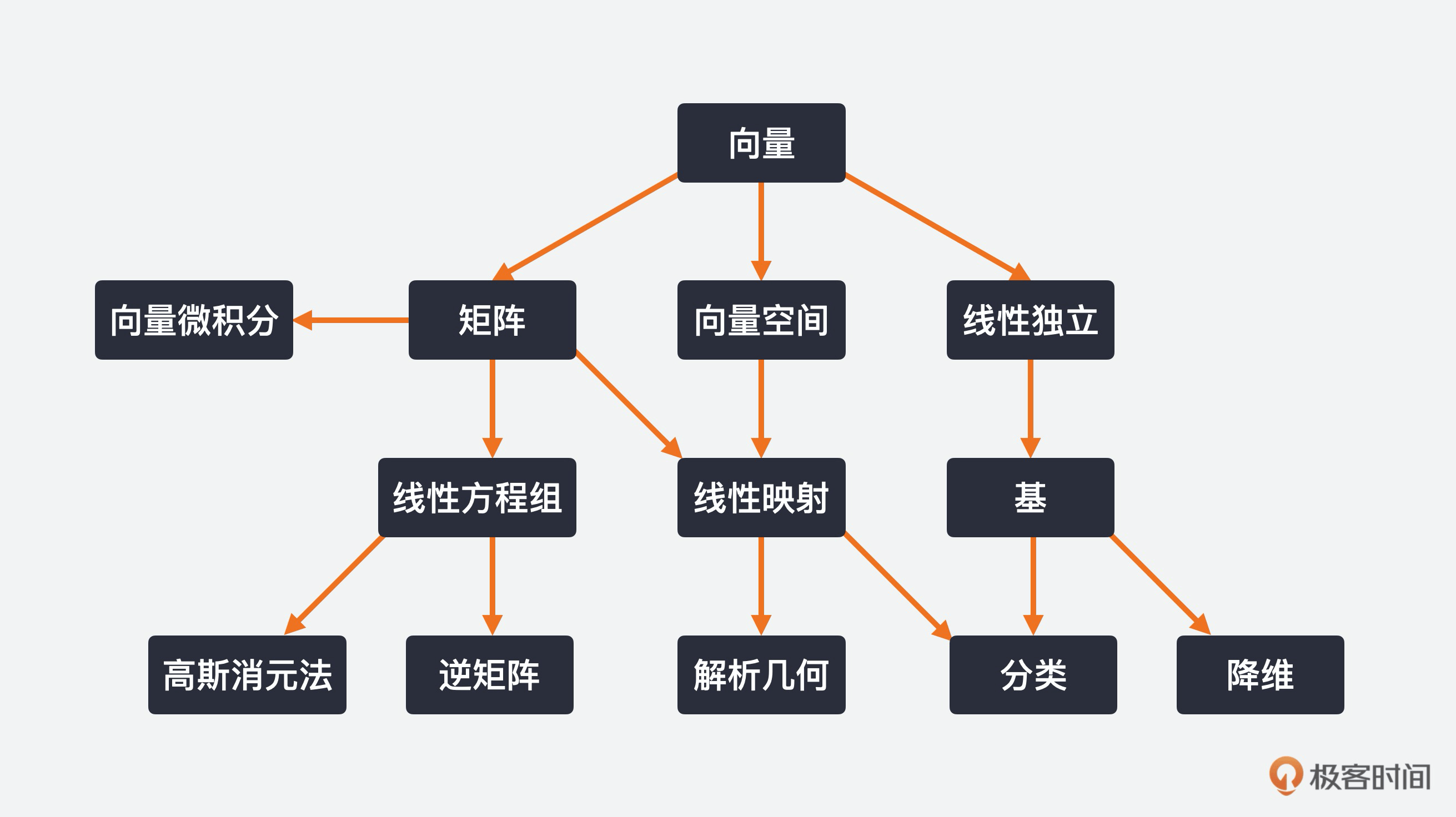
从图中最左侧这一列,我们可以看出,向量组合成矩阵,矩阵可以表示成线性方程组,而线性方程组可以通过高斯消元法求解,也可以求逆矩阵。
同时,向量又可以组合成向量空间,向量空间和矩阵都可以做线性映射或者线性变换,线性映射在实践中可以用在解析几何和分类问题中。
而且,向量和线性独立是强相关的,也就是说,线性独立指的是向量的线性独立,而线性独立又可以引出能够生成整个空间的基(Basis),基在实践中可以用在分类和降维中。
这里,我再额外提一个非常重要的、在数学中经常用到的概念——**封闭性**,或者俗称**闭包**(Closure)。封闭性的定义是,如果我们要对某个集合的成员进行一种运算,生成的仍然是这个集合的成员,那这个集合就可以称为在这个运算下闭合。
我为什么要提这个概念呢?这是因为,向量的线性运算是封闭的,也就是说向量的加法、数乘结果仍属于向量空间,即**向量的任意线性组合仍属于向量空间**。
## 线性方程组的应用
到这里,相信你已经对线性代数、向量这些基本概念有了一个应试教育之外的、新的认识,接下来我就切入本篇的最重点的内容了,那就是线性方程组。
线性方程组在线性代数中有着举足轻重的地位,许多现实生活中的问题都可以表达成线性方程组。关于线性方程组的概念,我想不用我多说了,这是初中的内容,你应该已经非常了解了。现在我举几个例子来说一说,线性方程组在现实生活中的运用,让你从应用的角度再理解下线性方程组。
第一个例子是计算旅游团人数。假设,一个旅游团由孩子和大人组成,去程时他们一起坐大巴,每个孩子的票价3元,大人票价3.2元,总共花费118.4元。回程时一起坐火车,每个孩子的票价3.5元,大人票价3.6元,总共花费135.2元。请问这个旅游团中有多少孩子和大人?
假设小孩人数为$x\_{1}$,大人人数为$x\_{2}$,于是我们得到了一个方程组:
$$\\left\\{\\begin{array}{c}
3 x\_{1}+3.2 x\_{2}=118.4 \\\\\\
3.5 x\_{1}+3.6 x\_{2}=135.2
\\end{array}\\right.$$
使用初中的解二元一次方程组的知识,我们可以得出这个方程组的解是:
$$\\left\\{\\begin{array}{c}
x\_{1}=16 \\\\\\
x\_{2}=22
\\end{array}\\right.$$
这个就是典型的线性方程组的现实例子。当然,我们也可以用矩阵来解这个方程组。你可能会说,这问题很简单啊,为什么还要用矩阵来解呢?整这么复杂有必要吗?别着急,这里我先卖个关子,具体我会在下一讲“矩阵篇”中进行讲解。
第二个例子是找出公司的最优生产计划。我们从公司的角度来看一看,假设生产苹果的几大主流产品:iPhone、Macbook、iMac,以及iWatch四款产品,需要用到芯片、摄像头模组、电池、IPS屏幕四大类资源,产品分别用 $N\_{1},N\_{2},N\_{3},N\_{4}$来表示,资源分别用$R\_{1},R\_{2},R\_{3},R\_{4}$来表示。
生产一单位的产品 $N\_{1}$,也就是iPhone,需要$a\_{11},a\_{21},a\_{31},a\_{41}$的资源,也就是芯片、摄像头模组、电池和IPS屏幕资源,其他产品也是一样。
我们的目标是在资源有限的情况下,找到一个最优生产计划,使每个产品的产出数量最大化。也就是说,在总共有$b\_{i}$个单位资源$R\_{i}$可用情况下,每个产品$N\_{i}$ 有多少单元 $x\_{i}$应该被生产。因此,我们可以得到一个下面这样的线性方程组:
$$\\left\\{\\begin{array}{l}
a\_{11} x\_{1}+a\_{12} x\_{2}+a\_{13} x\_{3}+a\_{14} x\_{4}=b\_{1} \\\\\\
a\_{21} x\_{1}+a\_{22} x\_{2}+a\_{23} x\_{3}+a\_{24} x\_{4}=b\_{2} \\\\\\
a\_{31} x\_{1}+a\_{32} x\_{2}+a\_{33} x\_{3}+a\_{34} x\_{4}=b\_{3} \\\\\\
a\_{41} x\_{1}+a\_{42} x\_{2}+a\_{43} x\_{3}+a\_{44} x\_{4}=b\_{4}
\\end{array}\\right.$$
于是,我们得到线性方程组的通用表达方式,$x\_{1},\\cdots ,x\_{n}$ 是未知变量,每个满足方程组表达式的n元组$(x\_{1},\\cdots ,x\_{n})$都是它的解。
$$\\left\\{\\begin{array}{l}
a\_{11} x\_{1}+a\_{12} x\_{2}+\\cdots+a\_{1 n} x\_{n}=b\_{1} \\\\\\
a\_{21} x\_{1}+a\_{22} x\_{2}+\\cdots+a\_{2 n} x\_{n}=b\_{2} \\\\\\
\\cdots \\cdots \\cdots \\cdots \\cdots \\cdots \\cdots \\cdots \\cdots \\cdots \\\\\\
a\_{m 1} x\_{1}+a\_{m 2} x\_{2}+\\cdots+a\_{m n} x\_{n}=b\_{m}
\\end{array}\\right.$$
线性方程组的解是有几何意义的,从几何角度出发,有利于你理解和记忆线性方程组解的条件,接下来我们先来看看线性方程组解的几种情况,之后我再具体讲解线性方程组的几何表达。
首先我们来看**无解**的情况。假设有下面这样一个线性方程组:
$$\\left\\{\\begin{array}{c}
x\_{1}+x\_{2}+x\_{3}=3 \\\\\\
x\_{1}-x\_{2}+2 x\_{3}=2 \\\\\\
2 x\_{1}+3 x\_{3}=1
\\end{array}\\right.$$
第一行和第二行相加后,我们可以得到$2 x\_{1}+3 x\_{3}=5$,很明显,这个方程和第三行是矛盾的,所以,这个线性方程组无解。
其次是**只有一个解**的情况。假设有下面这样一个线性方程组:
$$\\left\\{\\begin{array}{c}
x\_{1}+x\_{2}+x\_{3}=3 \\\\\\
x\_{1}-x\_{2}+2 x\_{3}=2 \\\\\\
x\_{2}+x\_{3}=2
\\end{array}\\right.$$
这个方程组求解很简单,第一行乘以$-1$和第二行相加得到$-2x\_{2}+x\_{3}=-1$,再乘以$-1$后和第三行相加得到$x\_{1}=1$,第一行和第二行相加,得到$2 x\_{1}+3 x\_{3}=5$ ,代入$x\_{1}$后,得到$x\_{3}=1$,最后,我们可以得到$(1,1,1)$是这个线性方程组的唯一解。
最后是**无穷解**的情况。我们有下面这样一个线性方程组:
$$\\left\\{\\begin{array}{c}
x\_{1}+x\_{2}+x\_{3}=3 \\\\\\
x\_{1}-x\_{2}+2 x\_{3}=2 \\\\\\
2 x\_{1}+3 x\_{3}=5
\\end{array}\\right.$$
方程组第一行和第二行相加等于第三行,从这个角度来说,我们就可以定义一个自由变量$x\_{3}=a$ ,$a$属于实数,那方程组的解就是:
$$\\left(\\frac{5}{2}-\\frac{3}{2} a, \\frac{1}{2}+\\frac{1}{2} a, a\\right)$$
其中$a$属于实数,所以,这就包含了无穷多个解。
## 线性方程组的几何表达
好了,了解了线性方程组解的三种情况,现在我们是时候从几何的角度来看一看线性方程组和它的解了,从几何意义出发有利于你更直观地理解线性方程组。
在一个只有两个变量$x\_{1},x\_{2}$的线性方程组中,我们定义一个$x\_{1},x\_{2}$平面。在这个平面中,每个线性方程都表达了一条直线。由于线性方程组的唯一解必须同时满足所有的等式,所以,线性方程组的唯一解其实就是线段的相交点,无穷解就是两线重合,而无解的情况,也就是两条线平行。
我拿一个例子来说明,设线性方程组:
$$\\left\\{\\begin{array}{l}
4 x\_{1}+4 x\_{2}=5 \\\\\\
2 x\_{1}-4 x\_{2}=1
\\end{array}\\right.$$
把其中的两个线性方程在$x\_{1},x\_{2}$平面中画出来后,我们可以得到两线段的交点$\\left(1, \\frac{1}{4}\\right)$,也就是这个线性方程组的解。
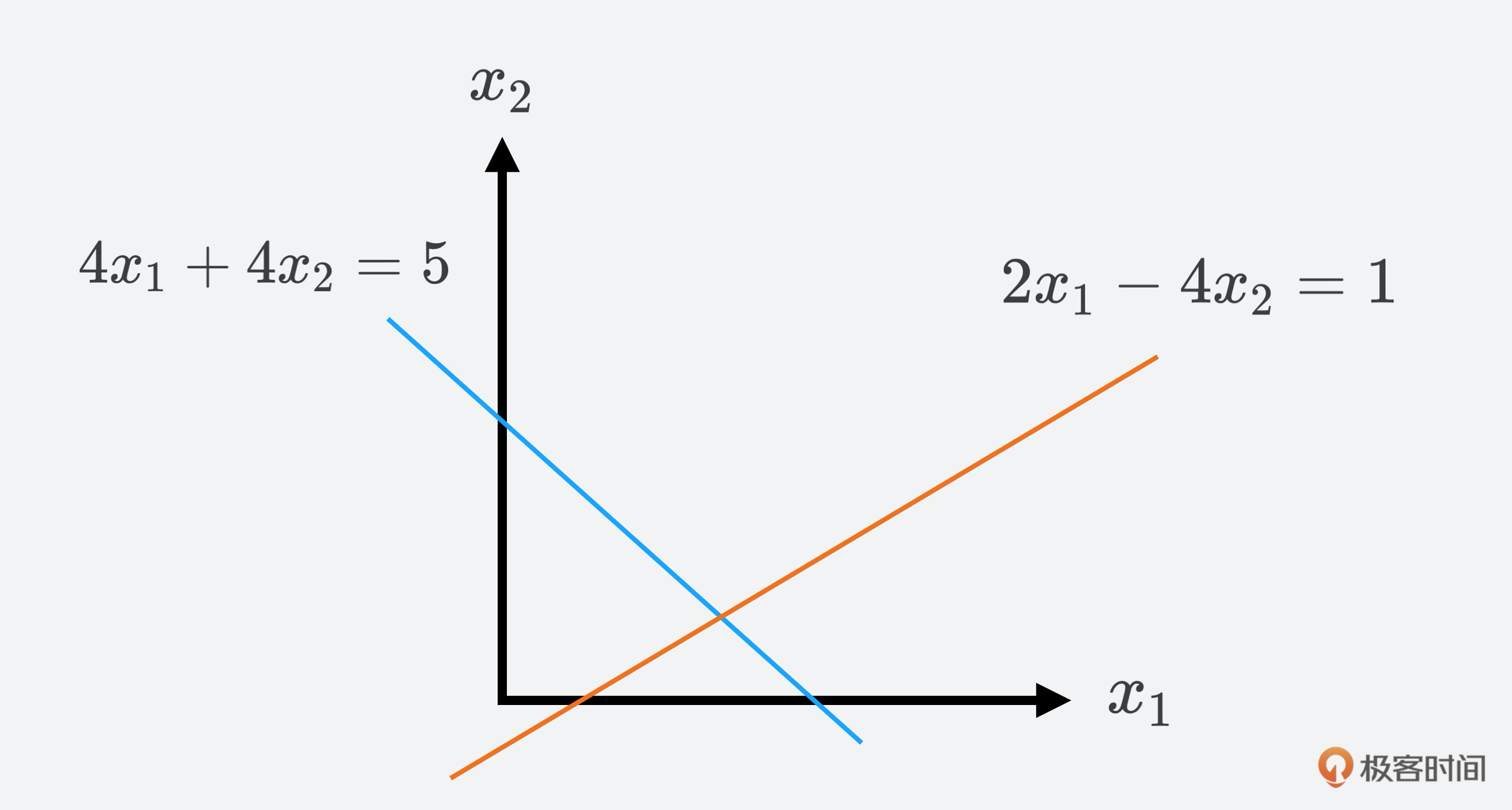
我再把这个概念延伸一下,当遇到三个变量的情况时,每个线性方程在三维空间中表达了一个平面,由于线性方程组的一个解必须同时满足所有的等式,所以,**线性方程组的解其实就是平面,也可以是线、点或者空,空也就是没有共同的平面相交**。
其实还有一个更好的方法来表达和解线性方程组,这个方法就是下一篇要讲的矩阵,在这里我先简单提一下。我们把系数组合成向量,把向量组合成矩阵,也就是说,我们可以把线性方程组写成这样的形式:
$$x\_{1}\\left|\\begin{array}{c}
a\_{11} \\\\\\
\\vdots \\\\\\
a\_{m 1}
\\end{array}\\right|+x\_{2}\\left|\\begin{array}{c}
a\_{12} \\\\\\
\\vdots \\\\\\
c\_{m 2}
\\end{array}\\right|+\\cdots+x\_{n}\\left|\\begin{array}{c}
a\_{1 n} \\\\\\
\\vdots \\\\\\
a\_{m n}
\\end{array}\\right|=\\left|\\begin{array}{c}
b\_{1} \\\\\\
\\vdots \\\\\\
b\_{m}
\\end{array}\\right|$$
再进一步最终可以写成矩阵的形式:
$$\\left\[\\begin{array}{cccc}
a\_{11} & a\_{12} & \\ldots & a\_{1 n} \\\\\\
a\_{21} & a\_{22} & \\ldots & a\_{2 n} \\\\\\
\\ldots & \\ldots & \\ldots & \\ldots \\\\\\
a\_{m 1} & a\_{m 2} & \\ldots & a\_{m n}
\\end{array}\\right\]\\left|\\begin{array}{c}
x\_{1} \\\\\\
\\vdots \\\\\\
. \\\\\\
x\_{n}
\\end{array}\\right|=\\left|\\begin{array}{c}
b\_{1} \\\\\\
\\vdots \\\\\\
. \\\\\\
b\_{m}
\\end{array}\\right|$$
## 本节小结
好了,到这里这一讲就结束了,我带你总结一下前面讲解的内容。
这节课我带你重新认识了代数和线性代数的概念。代数是构造一系列对象和一系列操作这些对象的规则,线性代数是向量,以及操作这些向量的规则,所以,线性代数是代数的具像化表达。从线性代数,我们引出了向量的基本概念,我带你看了一个和向量有关的所有概念,即线性代数所有核心内容的图。
可以说,线性代数的一切皆从**向量**而来。
最后,我带你从二维平面几何角度,更直观地观察线性方程组和它几种解的情况,**而二维空间的线性方程组的解其实就是线、点或者空,也就是没有共同的线段相交**。你也可以自己试着把它扩展到三维空间几何中来观察,或许会更有趣哦!
## 线性代数练习场
我们一起来看一个练习题。这是一道极其简单的初中线性方程组题,你可以回顾一下,也为下一节课做好铺垫。
李大叔去年承包了10亩地,种植甲、乙两种蔬菜,共获利18000元。其中甲蔬菜每亩获利2000元,乙蔬菜每亩获利1500元。
请问,李大叔去年甲、乙两种蔬菜各种植了多少亩?
欢迎在留言区晒出你的运算过程和结果。如果有收获,也欢迎你把这篇文章分享给你的朋友。