401 lines
23 KiB
Markdown
401 lines
23 KiB
Markdown
# 07 | 代码优化:跟编译器做朋友,让你的代码飞起来
|
||
|
||
你好,我是宫文学。
|
||
|
||
一门语言的性能高低,是它能否成功的关键。拿JavaScript来说,十多年来,它的性能多次得到成倍的提升,这也是前端技术栈如此丰富和强大的根本原因。
|
||
|
||
因此,编译器会无所不用其极地做优化,而优化工作在编译器的运行时间中,也占据了很大的比例。
|
||
|
||
不过,对编译技术的初学者来说,通常会搞不清楚编译器到底做了哪些优化,这些优化的实现思路又是怎样的。
|
||
|
||
所以今天这一讲,我就重点给你普及下编译器所做的优化工作,及其工作原理。在这个过程中,你还会弄明白很多似曾相识的术语,比如在前端必须了解的AST、终结符、非终结符等,在中后端必须熟悉的常数折叠、值编号、公共子表达式消除等。只有这样,你才算是入门了。
|
||
|
||
首先,我带你认识一些常见的代码优化方法。
|
||
|
||
## 常见的代码优化方法
|
||
|
||
对代码做优化的方法有很多。如果要把它们分一下类的话,可以按照下面两个维度:
|
||
|
||
* **第一个分类维度,是机器无关的优化与机器相关的优化。**机器无关的优化与硬件特征无关,比如把常数值在编译期计算出来(常数折叠)。而机器相关的优化则需要利用某硬件特有的特征,比如SIMD指令可以在一条指令里完成多个数据的计算。
|
||
* **第二个分类维度,是优化的范围。**本地优化是针对一个基本块中的代码,全局优化是针对整个函数(或过程),过程间优化则能够跨越多个函数(或过程)做优化。
|
||
|
||
但优化算法很多,仅仅按照这两个维度分类,仍显粗糙。所以,我就按照优化的实现思路再分分类,让你了解起来更轻松一些。
|
||
|
||
### 思路1:把常量提前计算出来
|
||
|
||
程序里的有些表达式,肯定能计算出一个常数值,那就不要等到运行时再去计算,干脆在编译期就计算出来。比如 “`x=2*3`”可以优化成“`x=6`”。这种优化方法,叫做**常数折叠(Constant Folding)**。
|
||
|
||
而如果你一旦知道x的值其实是一个常量,那你就可以把所有用到x的地方,替换成这个常量,这叫做**常数传播(Constant Propagation)**。如果有“`y=x*2`”这样一个语句,那么就能计算出来“`y=12`”。所以说,常数传播会导致更多的常数折叠。
|
||
|
||
就算不能引起新的常数折叠,比如说“`z=a+x`”,替换成“`z=a+6`”以后,计算速度也会更快。因为对于很多CPU来说,“`a+x`”和“`a+6`”对应的指令是不一样的。前者可能要生成两条指令(比如先把a放到寄存器上,再把x加上去),而后者用一条指令就行了,因为常数可以作为操作数。
|
||
|
||
更有用的是,常数传播可能导致分支判断条件是常量,因此导致一个分支的代码不需要被执行。这种优化叫做**稀疏有条件的常数传播(Sparse Conditional Constant Propagation)**。
|
||
|
||
```
|
||
a = 2
|
||
b = 3
|
||
if(a<b){ //判断语句去掉
|
||
... //直接执行这个代码块
|
||
}
|
||
else{
|
||
... //else分支会去掉
|
||
}
|
||
|
||
```
|
||
|
||
### 思路2:用低代价的方法做计算
|
||
|
||
完成相同的计算,可以用代价更低的方法。比如“`x=x+0`”这行代码,操作前后x没有任何变化,所以这样的代码可以删掉;又比如“`x=x*0`” 可以简化成“`x=0`”。这类利用代数运算的规则所做的简化,叫做**代数简化(Algebra Simplification)。**
|
||
|
||
对于很多CPU来说,乘法运算改成移位运算,速度会更快。比如,“`x*2`”等价于“`x<<1`”,“`x*9`”等价于“`x<<3+x`”。这种采用代价更低的运算的方法,也叫做**强度折减(Strength Reduction)**。
|
||
|
||
### 思路3:消除重复的计算
|
||
|
||
下面的示例代码中,第三行可以被替换成“`z:=2*x`”, 因为y的值就等于x。这个时候,可能x的值已经在寄存器中,所以直接采用x,运算速度会更快。这种优化叫做**拷贝传播(Copy Propagation)。**
|
||
|
||
```
|
||
x := a + b
|
||
y := x
|
||
z := 2 * y
|
||
|
||
```
|
||
|
||
**值编号(Value Numbering)**也能减少重复计算。值编号是把相同的值,在系统里给一个相同的编号,并且只计算一次即可。比如,[Wikipedia](https://en.wikipedia.org/wiki/Value_numbering)上的这个案例:
|
||
|
||
```
|
||
w := 3
|
||
x := 3
|
||
y := x + 4
|
||
z := w + 4
|
||
|
||
```
|
||
|
||
其中w和x的值是一样的,因此编号是相同的。这会进一步导致y和z的编号也是相同的。进而,它们可以简化成:
|
||
|
||
```
|
||
w := 3
|
||
x := w
|
||
y := w + 4
|
||
z := y
|
||
|
||
```
|
||
|
||
值编号又可以分为两种,本地值编号(在一个基本块中)和全局值编号(GVN,在一个函数范围内)。
|
||
|
||
还有一种优化方法叫做**公共子表达式消除(Common Subexpression Elimination,CSE),**也会减少计算次数。下面这两行代码,x和y右边的形式是一样的,如果这两行代码之间,a和b的值没有发生变化(比如采用SSA形式),那么x和y的值一定是一样的。
|
||
|
||
```
|
||
x := a + b
|
||
y := a + b
|
||
|
||
```
|
||
|
||
那我们就可以让y等于x,从而减少了一次对“`a+b`”的计算,这就是公共子表达式消除。
|
||
|
||
```
|
||
x := a + b
|
||
y := x
|
||
|
||
```
|
||
|
||
**部分冗余消除(Partial Redundancy Elimination,PRE)**,是公共子表达式消除的一种特殊情况。比如,这个来自[Wikipedia](https://en.wikipedia.org/wiki/Partial_redundancy_elimination)的例子中,一个分支有“`x+4`”这个公共子表达式,而另一个分支则没有。
|
||
|
||
```
|
||
if (some_condition) {
|
||
// some code that does not alter x
|
||
y = x + 4;
|
||
}
|
||
else {
|
||
// other code that does not alter x
|
||
}
|
||
z = x + 4;
|
||
|
||
```
|
||
|
||
但是,上述代码仍然可以优化,使得在if结构中,“`x+4`”这个值肯定会被计算一次,因此“`z=x+4`”就可以被优化。
|
||
|
||
```
|
||
if (some_condition) {
|
||
// some code that does not alter x
|
||
t = x + 4;
|
||
y = t;
|
||
}
|
||
else {
|
||
// other code that does not alter x
|
||
t = x + 4;
|
||
}
|
||
z = t;
|
||
|
||
```
|
||
|
||
### 思路4:化零为整,向量计算
|
||
|
||
很多CPU支持向量运算,也就是SIMD(Single Instruction Multiple Data)指令。这就可以在一条指令里计算多个数据。比如AVX-512指令集,可以使用512位的寄存器做运算,这个指令集的一条add指令相当于一次能把16个整数加到另16个整数上,以1当16呀。
|
||
|
||
比如,把16万个整数相加,应该怎样写程序呢?普通方法,是循环16万次,每次读1个数据,并做累加。向量化的方法,是每次读取16个,用AVX-512指令做加法计算,一共循环计算1万次,最后再把得到的16个数字相加就行了。
|
||
|
||
向量优化的一个例子是**超字级并行(Superword-Level Parallelism,SLP)**。它是把基本块中的多个变量组成一个向量,用一个指令完成多个变量的计算。
|
||
|
||
向量优化的另一个例子是**循环向量化(Loop Vectorization)**,我会在下面针对循环的优化思路中讲到它。
|
||
|
||
### 思路5:化整为零,各个优化
|
||
|
||
另一个思路是反着的,是化整为零。
|
||
|
||
很多语言都有结构和对象这样的复合数据类型,内部包含了多个成员变量,这种数据类型叫做**聚合体(aggregates)**。通常,为这些对象申请内存的时候,是一次就申请一整块,能放下里面的所有成员。但这样做,非常不利于做优化。
|
||
|
||
通常的优化算法都是针对标量(Scalar)的。如果经过分析,发现可以把聚合体打散,像使用单个本地变量(也就是标量)一样使用聚合体的成员变量,那就有可能带来其他优化的机会。比如,可以把聚合体的成员变量放在寄存器中进行计算,根本不需要访问内存。
|
||
|
||
这种优化叫做**聚合体的标量替换(Scalar Replacement of Aggregates,SROA)。**在研究Java的JIT编译器时,我们会见到一个这类优化的例子。
|
||
|
||
### 思路6:针对循环,重点优化
|
||
|
||
在编译器中,对循环的优化从来都是重点,因为程序中最多的计算量都是被各种循环消耗掉的。所以,对循环做优化,会起到事半功倍的效果。如果一个循环执行了10000次,那么你的优化效果就会被扩大10000倍。
|
||
|
||
对循环做优化,有很多种方法,我来和你介绍几种常用的。
|
||
|
||
**第一种:归纳变量优化(Induction Variable Optimization)。**
|
||
|
||
看下面这个循环,其中的变量j是由循环变量派生出来的,这种变量叫做该循环的归纳变量。归纳变量的变化是很有规律的,因此可以尝试做**强度折减**优化。示例代码中的乘法可以由加法替代。
|
||
|
||
```
|
||
int j = 0;
|
||
for (int i = 1; i < 100; i++) {
|
||
j = 2*i; //2*i可以替换成j+2
|
||
}
|
||
return j;
|
||
|
||
```
|
||
|
||
**第二种:边界检查消除(Unnecessary Bounds-checking Elimination)。**
|
||
|
||
当引用一个数组成员的时候,通常要检查下标是否越界。在循环里面,如果每次都要检查的话,代价就会相当高(例如做多个数组的向量运算的时候)。如果编译器能够确定,在循环中使用的数组下标(通常是循环变量或者基于循环变量的归纳变量)不会越界,那就可以消除掉边界检查的代码,从而大大提高性能。
|
||
|
||
**第三种:循环展开(Loop Unrolling)。**
|
||
|
||
把循环次数减少,但在每一次循环里,完成原来多次循环的工作量。比如:
|
||
|
||
```
|
||
for (int i = 0; i< 100; i++){
|
||
sum = sum + i;
|
||
}
|
||
|
||
```
|
||
|
||
优化后可以变成:
|
||
|
||
```
|
||
for (int i = 0; i< 100; i+=5){
|
||
sum = sum + i;
|
||
sum = sum + i + 1;
|
||
sum = sum + i + 2;
|
||
sum = sum + i + 3;
|
||
sum = sum + i + 4;
|
||
}
|
||
|
||
```
|
||
|
||
进一步,循环体内的5条语句就可以优化成1条语句:“`sum = sum + i*5 + 10;`”。
|
||
|
||
减少循环次数,本身就能减少循环条件的执行次数。同时,它还会增加一个基本块中的指令数量,从而为指令排序的优化算法创造机会。指令排序会在下一讲中介绍。
|
||
|
||
**第四种:循环向量化(Loop Vectorization)。**
|
||
|
||
在循环展开的基础上,我们有机会把多次计算优化成一个向量计算。比如,如果要循环16万次,对一个包含了16万个整数的数组做汇总,就可以变成循环1万次,每次用向量化的指令计算16个整数。
|
||
|
||
**第五种:重组(Reassociation)。**
|
||
|
||
在循环结构中,使用代数简化和重组,能获得更大的收益。比如,如下对数组的循环操作,其中数组`a[i,j]`的地址是“`a+i*N+j`”。但这个运算每次循环就要计算一次,一共要计算`M*N`次。但其实,这个地址表达式的前半截“`a+i*N`”不需要每次都在内循环里计算,只要在外循环计算就行了。
|
||
|
||
```
|
||
for (i = 0; i< M; i++){
|
||
for (j = 0; j<N; j++){
|
||
a[i,j] = b + a[i,j];
|
||
}
|
||
}
|
||
|
||
```
|
||
|
||
优化后的代码相当于:
|
||
|
||
```
|
||
for (i = 0; i< M; i++){
|
||
t=a+i*N;
|
||
for (j = 0; j<N; j++){
|
||
*(t+j) = b + *(t+j);
|
||
}
|
||
}
|
||
|
||
```
|
||
|
||
**第六种:循环不变代码外提(Loop-Invariant Code Motion,LICM)。**
|
||
|
||
在循环结构中,如果发现有些代码其实跟循环无关,那就应该提到循环外面去,避免一次次重复计算。
|
||
|
||
**第七种:代码提升(Code Hoisting,或Expression Hoisting)。**
|
||
|
||
在下面的if结构中,then块和else块都有“`z=x+y`”这个语句,它可以提到if语句的外面。
|
||
|
||
```
|
||
if (x > y)
|
||
...
|
||
z = x + y
|
||
...
|
||
}
|
||
else{
|
||
z = x + y
|
||
...
|
||
}
|
||
|
||
```
|
||
|
||
这样变换以后,至少代码量会降低。但是,如果这个if结构是在循环里面,那么可以继续借助**循环不变代码外提**优化,把“`z=x+y`”从循环体中提出来,从而降低计算量。
|
||
|
||
```
|
||
z = x + y
|
||
for(int i = 0; i < 10000; i++){
|
||
if (x > y)
|
||
...
|
||
}
|
||
else{
|
||
...
|
||
}
|
||
}
|
||
|
||
```
|
||
|
||
另外,前面说过的部分冗余优化,也可能会产生可以外提的代码,借助这一优化方法,可以形成进一步优化的效果。
|
||
|
||
针对循环能做的优化还有不少,因为对循环做优化往往是收益很高的!
|
||
|
||
### 思路7:减少过程调用的开销
|
||
|
||
你知道,当程序调用一个函数的时候,开销是很大的,比如保存原来的栈指针、保存某些寄存器的值、保存返回地址、设置参数,等等。其中很多都是内存读写操作,速度比较慢。
|
||
|
||
所以,如果能做一些优化,减少这些开销,那么带来的优化效果会是很显著的,具体的优化方法主要有下面几种。
|
||
|
||
**第一种:尾调用优化(Tail-call Optimization)和尾递归优化(Tail-recursion Elimination)。**
|
||
|
||
尾调用就是一个函数的最后一句,是对另一个函数的调用。比如,下面这段示例代码:
|
||
|
||
```
|
||
f(){
|
||
...
|
||
return g(a,b);
|
||
}
|
||
|
||
```
|
||
|
||
而如果g()本身就是f()的最后一行代码,那么f()的栈帧已经没有什么用了,可以撤销掉了(修改栈顶指针的值),然后直接跳转到g()的代码去执行,就像f()和g()是同一个函数一样。这样可以让g()复用f()的栈空间,减少内存消耗,也减少一些内存读写操作(比如,保护寄存器、写入返回地址等)。
|
||
|
||
如果f()和g()是同一个函数,这就叫做**尾递归**。很多同学都应该知道,尾递归是可以转化为一个循环的。我们在[第3讲](https://time.geekbang.org/column/article/244906)改写左递归文法为右递归文法的时候,就曾经用循环代替了递归调用。尾递归转化为循环,不但可以节省栈帧的开销,还可以进一步导致针对循环的各种优化。
|
||
|
||
**第二种:内联(inlining)。**
|
||
|
||
内联也叫做过程集成(Procedure Integration),就是把被调用函数的代码拷贝到调用者中,从而避免函数调用。
|
||
|
||
对于我们现在使用的面向对象的语言来说,有很多短方法,比如getter、settter方法。这些方法内联以后,不仅仅可以减少函数调用的开销,还可以带来其他的优化机会。在探究Java的JIT编译器时,我就会为你剖析一个内联的例子。
|
||
|
||
**第三种:内联扩展(In-Line Expansion)。**
|
||
|
||
内联扩展跟普通内联类似,也是在调用的地方展开代码。不过内联扩展被展开的代码,通常是手写的、高度优化的汇编代码。
|
||
|
||
**第四种:叶子程序优化(Leaf-Routine Optimization)。**
|
||
|
||
叶子程序,是指不会再调用其他程序的函数(或过程)。因此,它也可以对栈的使用做一些优化。比如,你甚至可以不用生成栈帧,因为根据某些调用约定,程序可以访问栈顶之外一定大小的内存。这样就省去了保存原来栈顶、修改栈顶指针等一系列操作。
|
||
|
||
### 思路8:对控制流做优化
|
||
|
||
通过对程序的控制流分析,我们可以发现很多优化的机会。这就好比在做公司管理,优化业务流程,就会提升经营效率。我们来看一下这方面的优化方法有哪些。
|
||
|
||
**第一种:不可达代码消除(Unreacheable-code Elimination)**。根据控制流的分析,发现有些代码是不可能到达的,可以直接删掉,比如return语句后面的代码。
|
||
|
||
**第二种:死代码删除(Dead-code Elimination)**。通过对流程的分析,发现某个变量赋值了以后,后面根本没有再用到这个变量。这样的代码就是死代码,就可以删除。
|
||
|
||
**第三种:If简化(If Simplification)**。在讲常量传播时我们就见到过,如果有可能if条件肯定为真或者假,那么就可以消除掉if结构中的then块、else块,甚至整个消除if结构。
|
||
|
||
**第四种:循环简化(Loop Simplification)**。也就是把空循环或者简单的循环,变成直线代码,从而增加了其他优化的机会,比如指令的流水线化。
|
||
|
||
**第五种:循环反转(Loop Inversion)**。这是对循环语句常做的一种优化,就是把一个while循环改成一个repeat…until循环(或者do…while循环)。这样会使基本块的结构更简化,从而更有利于其他优化。
|
||
|
||
**第六种:拉直(Straightening)**。如果发现两个基本块是线性连接的,那可以把它们合并,从而增加优化机会。
|
||
|
||
**第七种:反分支(Unswitching)**。也就是减少程序分支,因为分支会导致程序从一个基本块跳到另一个基本块,这样就不容易做优化。比如,把循环内部的if分支挪到循环外面去,先做if判断,然后再执行循环,这样总的执行if判断的次数就会减少,并且循环体里面的基本块不那么零碎,就更加容易优化。
|
||
|
||
这七种优化方法,都是对控制流的优化,有的减少了基本块,有的减少了分支,有的直接删除了无用的代码。
|
||
|
||
## 代码优化所依赖的分析方法
|
||
|
||
前面我列举了很多优化方法,目的是让你认识到编译器花费大量时间去做的,到底都是一些什么工作。当然了,我只是和你列举了最常用的一些优化方法,不过这已经足够帮助你建立对代码优化的直觉认知了。我们在研究具体的编译器的时候,还会见到其他一些优化方法。不过你不用担心,根据上面讲到的各种优化思路,你可以举一反三,非常快速地理解这些新的优化方法。
|
||
|
||
上述优化方法,有的比较简单,比如常数折叠,依据AST或MIR做点处理就可以完成。但有些优化,就需要比较复杂的分析方法做支撑才能完成。这些分析方法包括控制流分析、数据流分析、依赖分析和别名分析等。
|
||
|
||
**控制流分析(Control-Flow Analysis,CFA)**。控制流分析是帮助我们建立对程序执行过程的理解,比如哪里是程序入口,哪里是出口,哪些语句构成了一个基本块,基本块之间跳转关系,哪个结构是一个循环结构(从而去做循环优化),等等。
|
||
|
||
前面提到的控制流优化,就是要基于对控制流的正确理解。下面要讲的数据流分析算法,在做全局分析的时候,也要基于控制流图(CFG),所以也需要以控制流分析为基础。
|
||
|
||
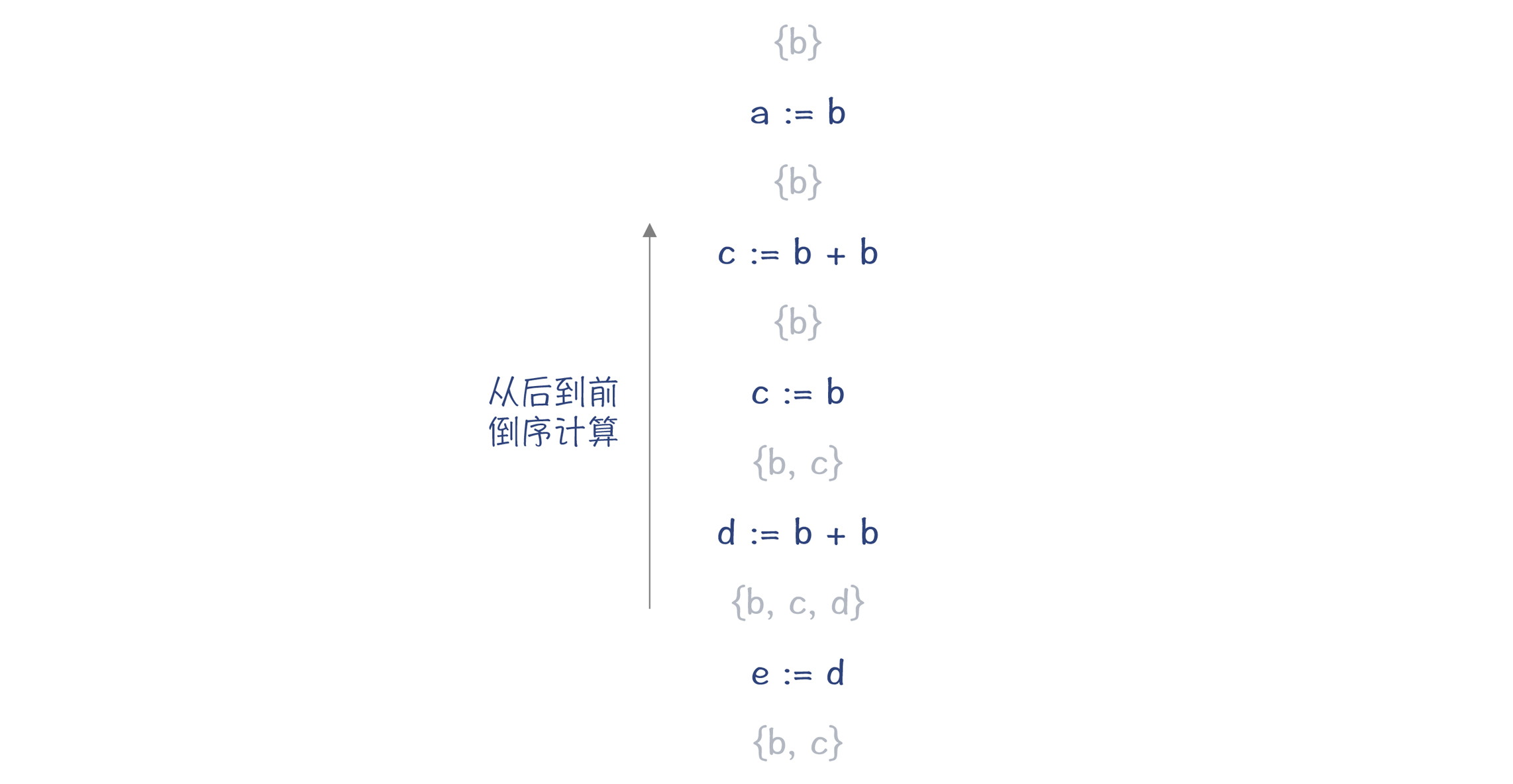
**数据流分析(Data-Flow Analysis,DFA)**。数据流分析,能够帮助我们理解程序中的数据变化情况。我们看一个分析变量活跃性的例子。
|
||
|
||
如下图所示,它从后到前顺序扫描代码,花括号中的是在当前位置需要的变量的集合。如果某个变量不被需要,那就可以做死代码删除的优化。
|
||
|
||
|
||
|
||
经过多遍扫描和删除后,最后的代码会精简成一行:
|
||
|
||
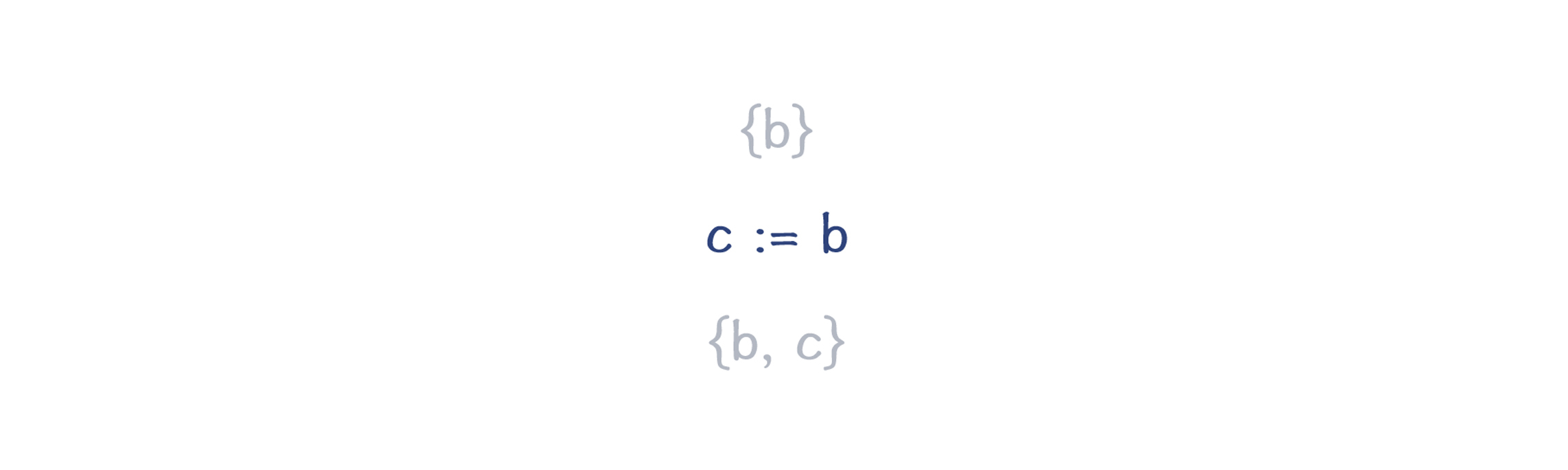
|
||
|
||
关于数据流分析框架的详细描述,你可以再参考下其他资料(比如,《编译原理之美》专栏第[27](https://time.geekbang.org/column/article/155338)和[28](https://time.geekbang.org/column/article/156878)两讲)。
|
||
|
||
除了做变量活跃性分析以外,数据流分析方法还可以做很多有用的分析。比如,可达定义分析(Reaching Definitions Analysis)、可用表达式分析(Available Expressions Analysis)、向上暴露使用分析(Upward Exposed Uses Analysis)、拷贝传播分析(Copy-Propagation Analysis)、常量传播分析(Constant-Propagation Analysis)、局部冗余分析(Partial-Redundancy Analysis)等。
|
||
|
||
就像基于变量活跃性分析可以做死代码删除的优化一样,上述分析是做其他很多优化的基础。
|
||
|
||
**依赖分析(Dependency Analysis)**。依赖分析,就是分析出程序代码的控制依赖(Control Dependency)和数据依赖(Data Dependency)关系。这对指令排序和缓存优化很重要。
|
||
|
||
指令排序会在下一讲介绍。它能通过调整指令之间的顺序来提升执行效率。但指令排序不能打破指令间的依赖关系,否则程序的执行就不正确。
|
||
|
||
**别名分析(Alias Analysis)**。在C、C++等可以使用指针的语言中,同一个内存地址可能会有多个别名,因为不同的指针都可能指向同一个地址。编译器需要知道不同变量是否是别名关系,以便决定能否做某些优化。
|
||
|
||
好了,你已经了解了优化的方法和所依赖的分析方法。那么,这些方法这么多,哪些优化方法更重要,优化的顺序又是什么呢?
|
||
|
||
## 优化方法的重要性和顺序
|
||
|
||
我们先看看哪些优化方法更重要。
|
||
|
||
有些优化,比如对循环的优化,对每门语言都很重要,因为循环优化的收益很大。
|
||
|
||
而有些优化,对于特定的语言更加重要。在课程后面分析像Java、JavaScript这样的面向对象的现代语言时,你会看到,内联优化和逃逸分析的收益就比较大。而对于某些频繁使用尾递归的函数式编程语言来说,尾递归的优化就必不可少,否则性能损失太大。
|
||
|
||
至于优化的顺序,有的优化适合在早期做(基于HIR和MIR),有的优化适合在后期做(基于LIR和机器代码)。并且,你通过前面的例子也可以看到,一般做完某个优化以后,会给别的优化带来机会,所以经常会在执行某个优化算法的时候,调用了另一个优化算法,而同样的优化算法也可能会运行好几遍。
|
||
|
||
## 课程小结
|
||
|
||
今天这讲,我带你认识了很多常见的优化方法和背后的分析方法。我们很难一下子记住所有的方法,但完全可以先对这些概念建立总体印象。这样可以避免在研究具体编译器时,我们产生“瞎子摸象”的感觉。
|
||
|
||
另外,熟悉我提到的那些名词术语也很重要,因为它们经常在代码注释和相关文献里出现。这些名词要成为你的一项基本功。
|
||
|
||
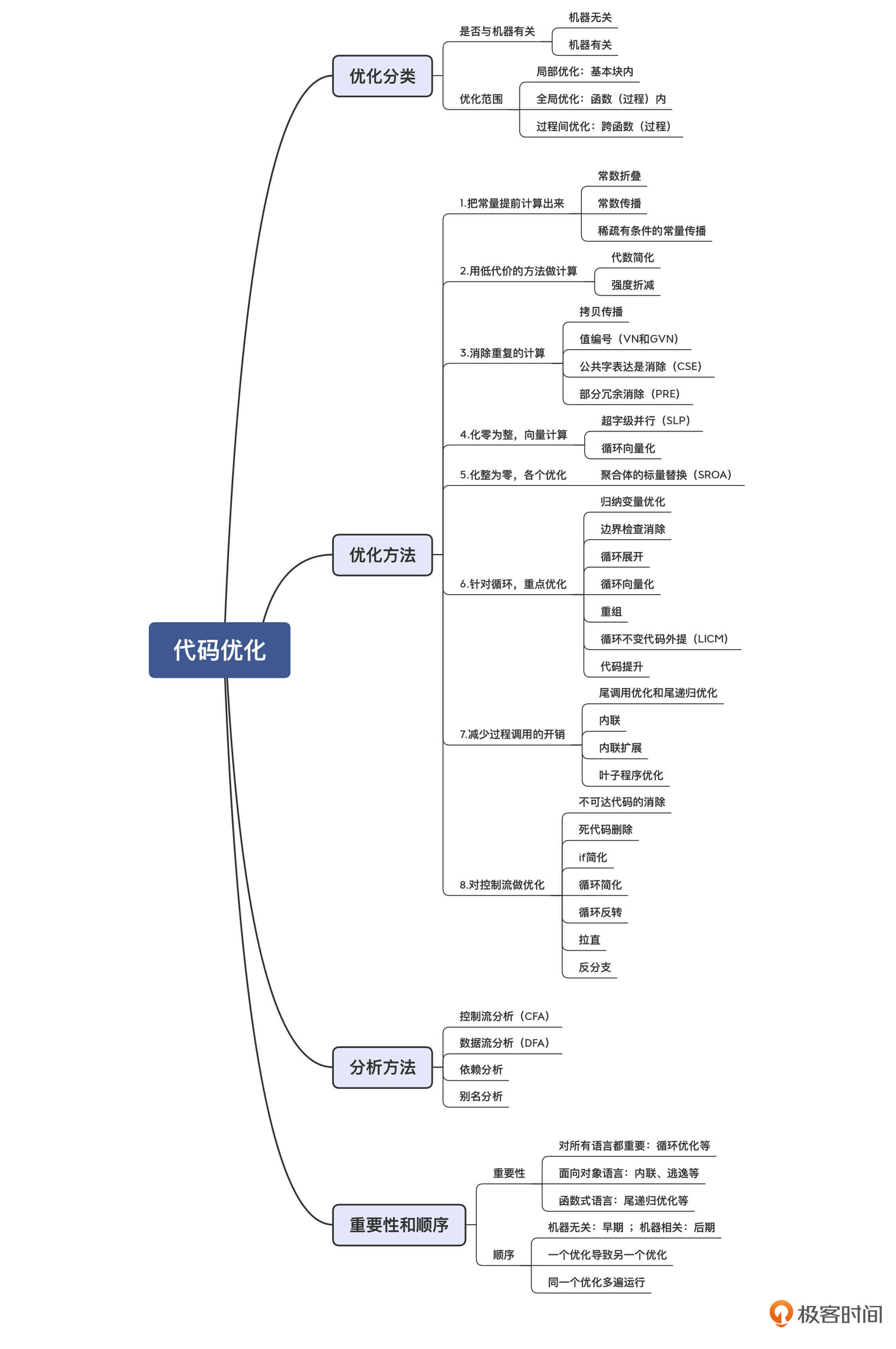
我把今天的课程内容,也整理成了思维导图,供你复习、参考。
|
||
|
||
|
||
|
||
在课程的第二个模块“真实编译器解析篇”的时候,我会和你分析某些优化算法具体的实现细节,并带你跟踪编译优化的过程。
|
||
|
||
根据我的经验,当你写的程序对性能要求很高的时候,你需要能够跟踪了解编译优化的过程,看看如何才能达到最好的优化效果。我之前写过与内存计算有关的程序,就特别关注如何才能让编译器做向量优化。因为是否使用向量,性能差别很大。现在做AI工作的同学,一定也有类似的需求。
|
||
|
||
还有些开源项目,它们的性能与内联关系密切。这就要做一定的调优,以确保使用频率最高、性能影响最大的函数全部内联。
|
||
|
||
还有,Chrome、Android和Flutter共同使用的二维图形引擎Skia对性能很敏感,所以即使在Windows平台上,仍然要求用Clang编译。为啥坚持用Clang编译呢?因为Skia跟LLVM的优化方法是紧密配合的,换了其他编译器就达不到这么好的优化效果。
|
||
|
||
类似的例子还有很多。了解优化,能够充分利用编译器的优化能力,应该是我们想拥有的一项高级技能。
|
||
|
||
## 一课一思
|
||
|
||
你可以比较一下值编号和公共子表达式消除这两个优化方法,说说它们的相同点和不同点吗?你能举出一个例子来,是其中一个算法能做优化,而另一个算法不能的吗?
|
||
|
||
欢迎在留言区中分享你的思考,也欢迎你把这节课分享给你的朋友。
|
||
|
||
## 参考资料
|
||
|
||
1. 龙书(Compilers Principles, Techniques and Tools):第9章,机器无关的优化,里面介绍了各种优化算法。
|
||
2. 鲸书(Advanced Compiler Design and Implementation)中讲优化的算法有很多,第7~15章你都可以看看。
|
||
|