12 KiB
24 | 一致性哈希:如何高效地均衡负载?
你好,我是陶辉。
还记得我们在[第22讲] 谈到的Cassandra数据库吗?它将服务器节点组成一个环来存储数据,所使用的就是一致性哈希算法。那这一讲,我们就来看看一致性哈希算法是怎样工作的。
使用哈希算法扩展系统时,最大的问题在于代表哈希桶的服务器节点数发生变化时,哈希函数就改变了,数据与节点间的映射关系自然发生了变化,结果大量数据就得在服务器间迁移。特别是含有多份冗余数据的系统,迁移工作量更是会成倍提高。
同时,为了在整体上更加充分地使用IT资源,我们必须解决分布式系统扩展时可能出现的两个问题:数据分布不均衡和访问量不均衡。比如,对于包含10个服务器节点、持久化1亿条用户数据的有状态服务,如果采用关键字模10(key%10)的哈希算法作为路由策略,就很难保证每个节点处理1千万条数据,那些可能还未达到一半设计容量的节点会浪费大量磁盘空间。
即使节点间存储的数据非常均匀,但这些数据间的活跃程度也不相同,存放热点数据较多的节点访问量非常大,很容易率先达到CPU瓶颈,在许多主机节点还很空闲时,我们就得扩容系统。
特别是我们很难保证集群内的所有节点都是同构的,如果哈希算法不能区别对待不同配置的服务器,也会抬高IT成本。
一致性哈希算法可以解决上述问题,它在许多流行的开源软件上都有很广泛的应用。这一讲我们将介绍一致性哈希算法的工作原理,以及如何通过虚拟节点提升算法的均衡性。
如何减少扩容、缩容时迁移的数据量?
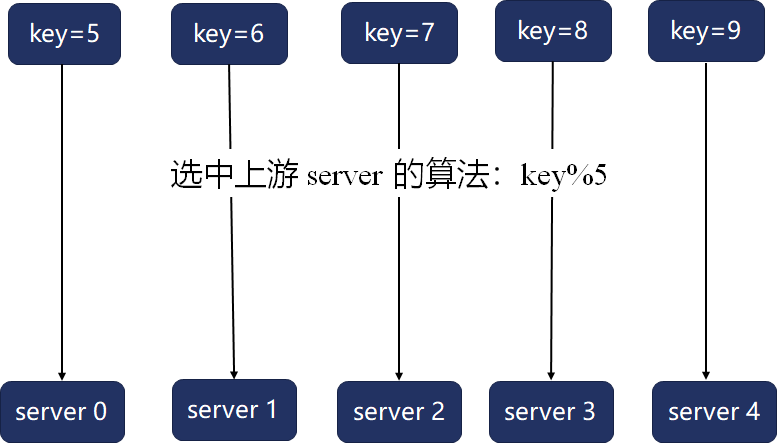
在主机硬件达到性能瓶颈后,有状态服务可以沿AKF立方体Z轴(参见[第21讲]),基于哈希算法扩展为分布式系统。下图系统中拥有5个节点,哈希算法将每条数据的关键字模5得出的数字作为哈希桶序号,从而将数据映射到节点上(如果关键字是字符串或者其他结构化数据,可以先通过其他哈希算法转换为整数,再进行模运算):
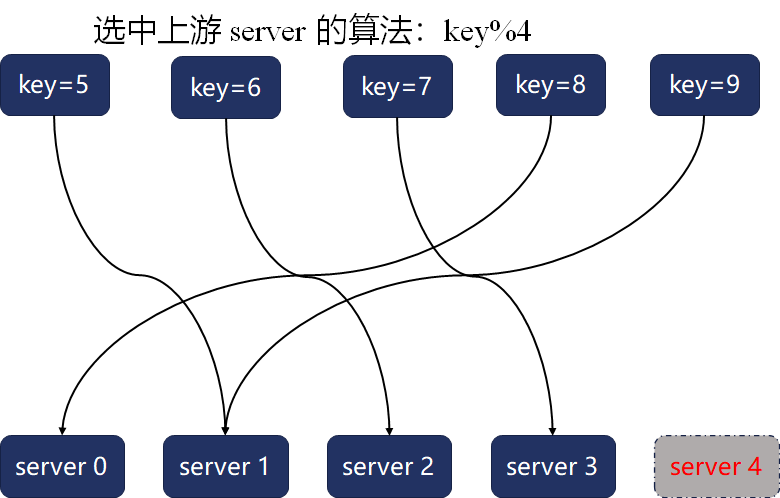
这个方案实现简单,运算速度也快,但它最大的问题是在系统扩容或者缩容时,必须迁移改变了映射关系的数据。然而,取模哈希函数中基数的变化,往往会导致绝大部分映射关系改变,比如上例中的5个关键字,在下图中集群节点数(即基数)从5降为4时,原映射关系全部失效,这5条数据都得迁移到其他节点:
1997年发布的《Consistent Hashing and Random Trees》论文提出了一致性哈希算法,可以大幅度减少数据迁移量。一致性哈希算法是通过以下2个步骤来建立数据与主机节点间映射关系的:
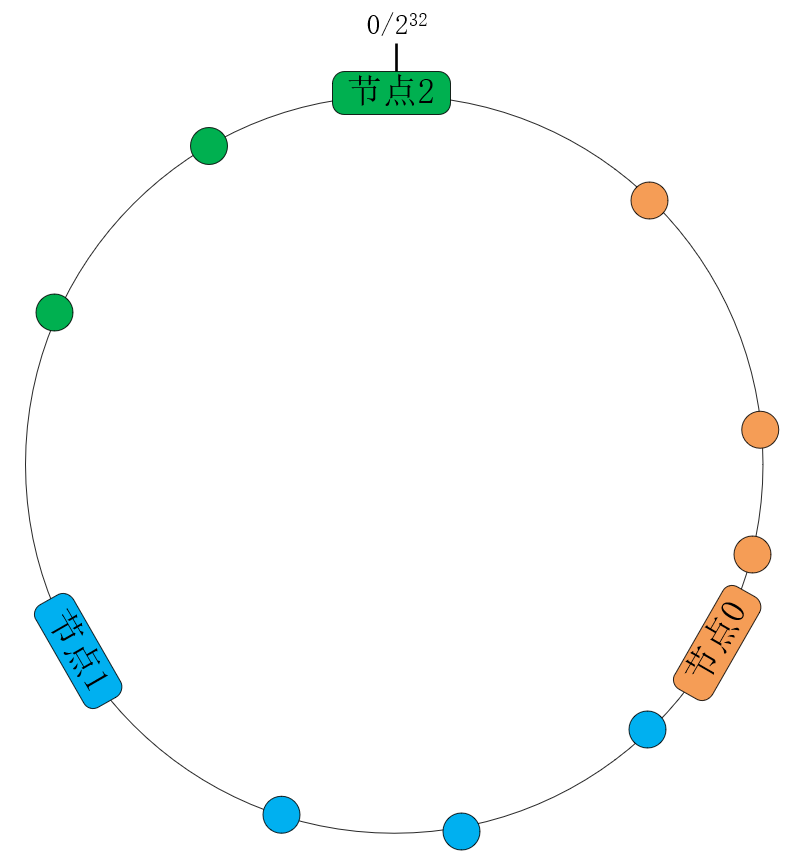
- 首先,将关键字经由通用的哈希函数映射为32位整型哈希值。这些哈希值会形成1个环,最大的数字
{2^{32}}相当于0。 - 其次,设集群节点数为N,将哈希环由小至大分成N段,每个主机节点处理哈希值落在该段内的数据。比如下图中,当节点数N等于3且均匀地分段时,节点0处理哈希值在 [0, $\frac{1}{3} * {2^{32}}$] 范围内的关键字,节点1处理 [
\\frac{1}{3} \* {2^{32}}, $\frac{2}{3} * {2^{32}}$] 范围内的关键字,而节点2则处理的范围是 [\\frac{2}{3} \* {2^{32}}, ${2^{32}}$]:
**当然,在生产环境中主机节点很可能是异构的,所以我们要给高规格的服务器节点赋予更高的权重。一致性哈希算法改变节点的权重非常简单,只需要给每个节点分配更大的弧长即可。**例如,如果上图中的节点0拥有更高的硬件配置,那么可以将原本均匀分布的3个节点调整为2:1:1的权重,这样节点0处理的哈希值范围调整为 [0, ${2^{31}}$],节点1的处理范围调整为 [{2^{31}}, ${3} * {2^{30}}$],节点2的处理范围调整为 [{3} \* {2^{30}}, ${2^{32}}$],如下图所示:
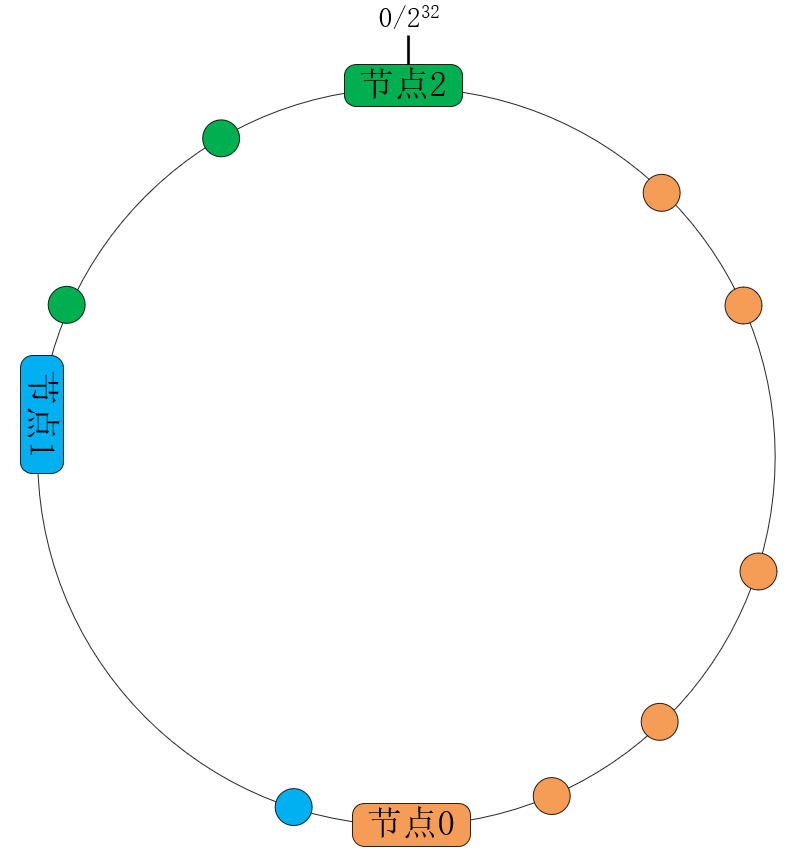
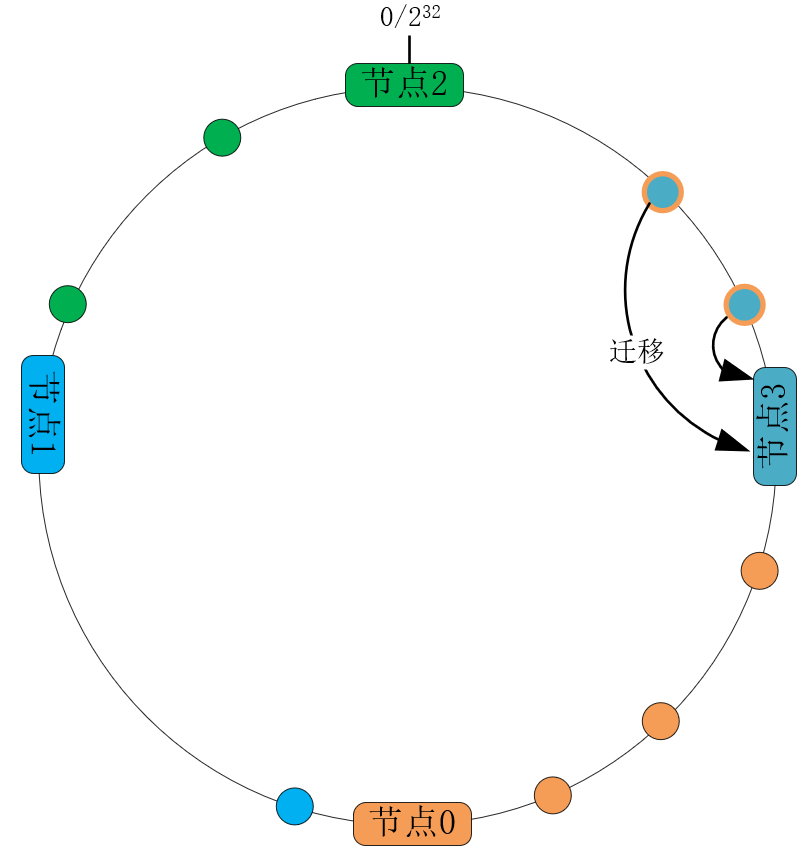
而扩容、缩容时,虽然节点数发生了变化,但只要小幅度调整环上各节点的位置,就不会导致大量数据的迁移。比如下图中我们将3个节点的集群扩容为4个节点,只需要将节点0上一半的数据迁移至节点3即可,其他节点不受影响:
接下来我们从成本上分析下一致性哈希算法的优劣。假设总数据条数为M,而节点个数为N,先来看映射函数的时间复杂度。传统的哈希算法以N为基数执行取模运算,时间复杂度为O(1)(参见[第3讲]);一致性哈希算法需要将关键字先转换为32位整型(这1步的时间复杂度也是O(1)),再根据哈希环中各节点的处理范围,找到所属的节点。由于所有节点是有序排列的,所以采用二分法,可以在O(logN)时间复杂度内,完成关键字到节点位置的映射。
再来评估下数据的迁移规模。节点变化会导致传统哈希算法的映射结果不可控,最坏情况下所有数据都需要迁移,所以它的数据迁移规模是O(M);对于一致性哈希算法,我们可以通过调整节点位置,任意设定迁移规模。在环中各节点均匀分布的情况下,数据迁移规模是O(M/N)。
因此,一致性哈希算法的缺点是将映射函数的时间复杂度从O(1)提高到了O(logN),它的优点是将数据迁移规模从O(M)降低至O(M/N)。由于数据条数M远大于主机节点数N,而且数据迁移的成本很大,所以一致性哈希算法更划算,它的适用场景也更广!
如何通过虚拟节点提高均衡度?
一致性哈希算法虽然降低了数据的迁移量,但却遗留了两个问题没有解决。
首先,如果映射后哈希环中的数字分布不均匀,就会导致各节点处理的数据不均衡,从而降低了系统的运行效率与性能。在无法找出分布规律时,我们也无法通过调整环中节点的权重,平衡各节点处理的数据量。
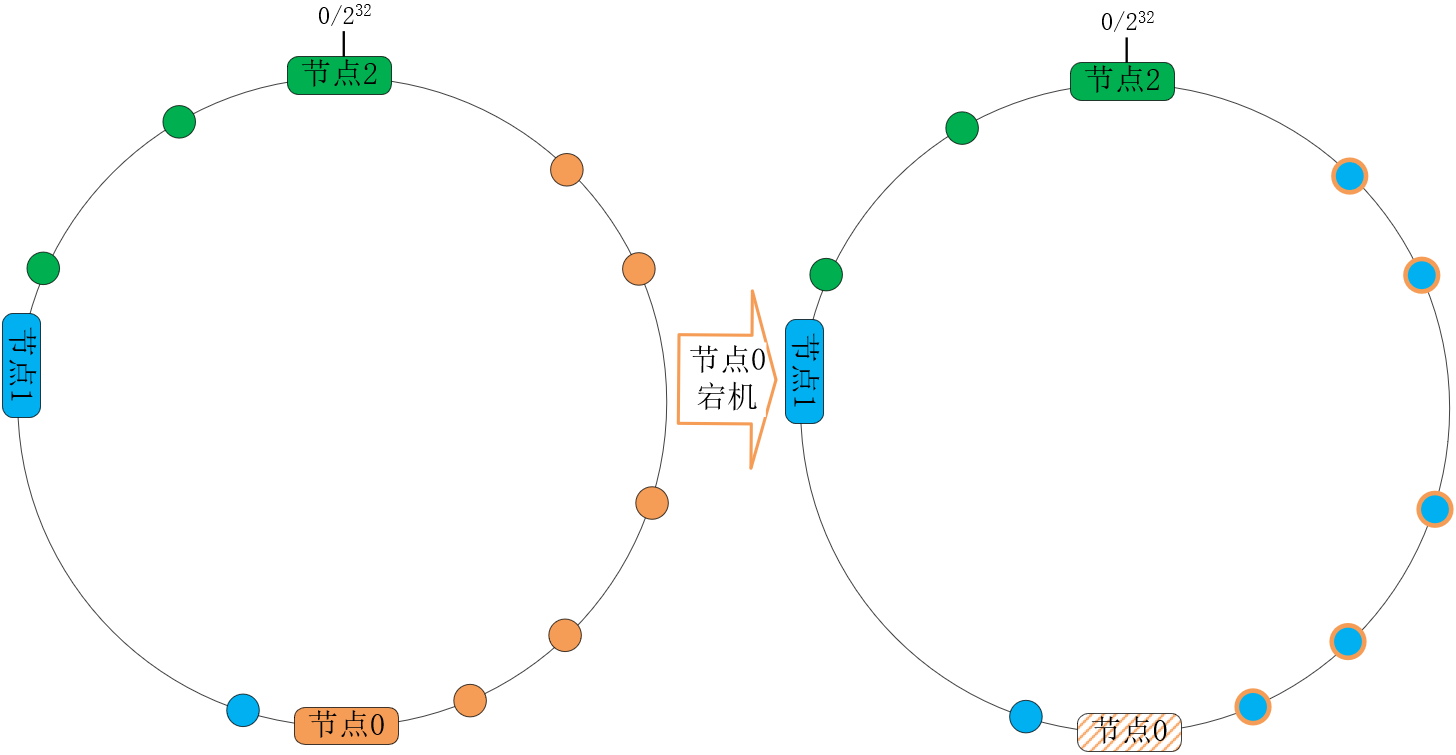
其次,容灾与扩容时,哈希环上的相邻节点容易受到过大影响。比如下图中,当节点0宕机后,根据一致性哈希算法的规则,其上数据应该全部迁移到相邻的节点1上,这样,节点1的数据量、访问量都会迅速增加1倍,一旦新增的压力超过了节点1的处理能力上限,就会导致节点1崩溃,进而形成雪崩式的连锁反应:
系统扩容时也面临着同样的问题,除非同时调整环中各节点的位置,否则扩容节点也只会减轻相邻节点的负载。
当数据存在多份冗余时,这两类问题会被进一步放大。
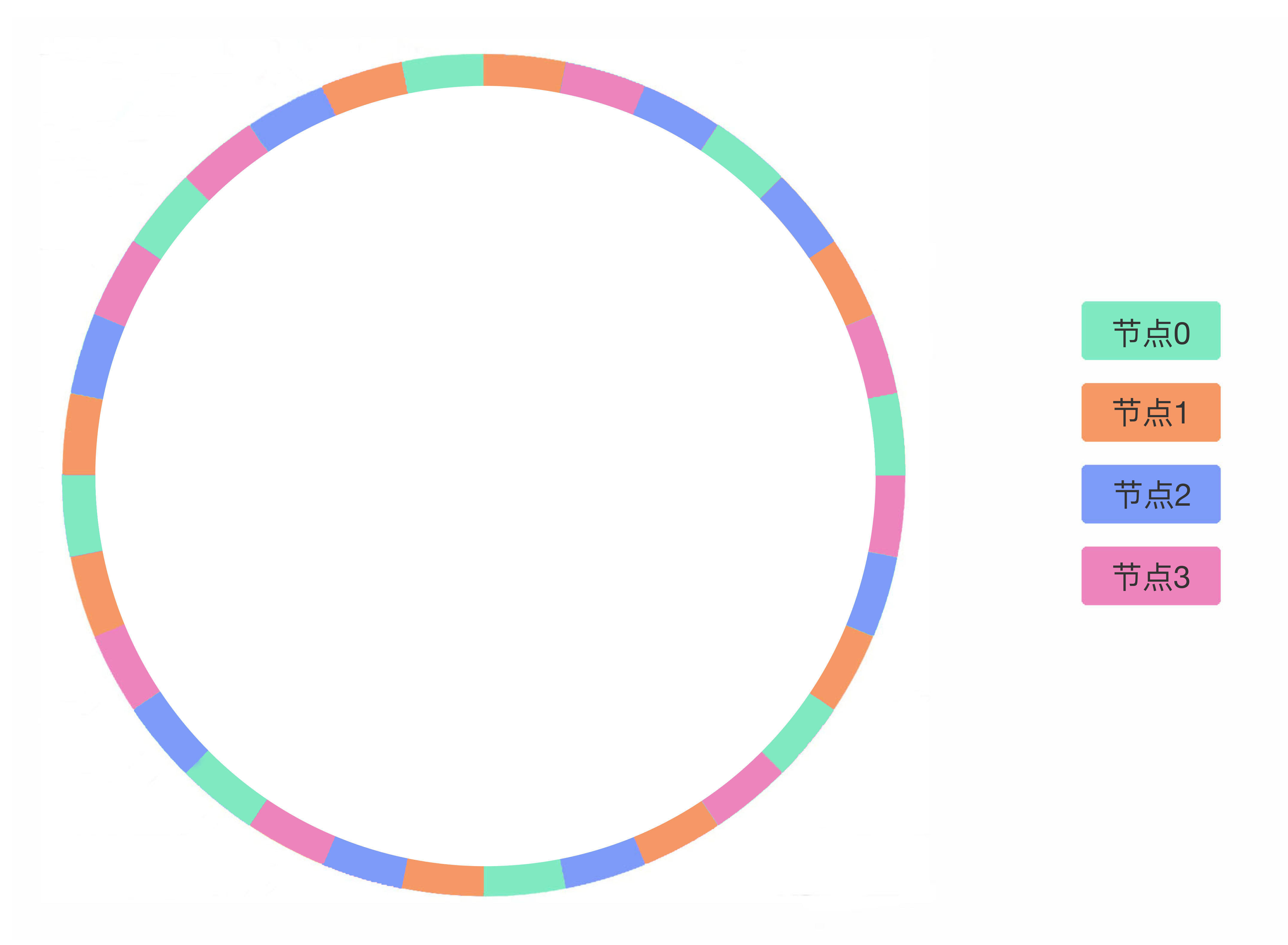
那如何提高均衡性呢?**在真实的数据节点与哈希环之间引入一个虚拟节点层,就可以解决上述问题。**例如下图中的集群含有4个节点,但我们并不直接将哈希环分为4份,而是将它均匀地分为32份并赋予32个虚拟节点,因此每个虚拟节点会处理 {2^{27}} 个哈希值,再将32个虚拟节点通过某个哈希函数(比如CRC32)映射到4个真实节点上(比如图中8个绿色虚拟节点皆由同色的主机节点0处理):
这样,如果图中绿色的节点0宕机,按照哈希环上数据的迁移规则,8个绿色虚拟节点上的数据就会沿着顺时针方向,分别迁移至相邻的虚拟节点上,最终会迁移到真实节点1(橙色)、节点2(蓝色)、节点3(水红色)上。所以,宕机节点上的数据会迁移到其他所有节点上。
扩容时也是一样的,通过虚拟节点环,新增节点可以分担现有全部节点的压力。至于虚拟节点为什么可以让数据的分布更均衡,这是因为在虚拟节点与真实节点间,又增加了一层哈希映射,哈希函数会将原本不均匀的数字进一步打散。上图为了方便你理解,每个真实节点仅包含8个虚拟节点,这样能起到的均衡效果其实很有限。而在实际的工程中,虚拟节点的数量会大很多,比如Nginx的一致性哈希算法,每个权重为1的真实节点就含有160个虚拟节点。
当然,有了虚拟节点后,为异构的服务器节点设置权重也更方便。只需要为权重高的真实节点,赋予更多的虚拟节点即可。注意,虚拟节点增多虽然会提升均衡性,但也会消耗更多的内存与计算力。
上面我们仅讨论了数据分布的均衡性,当热点数据导致访问量不均衡时,因为这一新维度的信息还没有反馈在系统中,所以你需要搜集各节点的访问量信息,基于它来动态地调整真实节点的权重,进而从热点数据更多的节点中迁移出部分数据,以此提高均衡性。
小结
这一讲我们介绍了一致性哈希算法的工作原理。
传统哈希函数中,主机节点的变化会导致大量数据发生迁移。一致性哈希算法将32位哈希值构成环,并将它分段赋予各节点,这样,扩容、缩容动作就只影响相邻节点,大幅度减少了数据迁移量。一致性哈希算法虽然将数据的迁移量从O(M)降为O(M/N),却也将映射函数的时间复杂度从O(1)提高到O(logN),但由于节点数量N并不会很大,所以一致性哈希算法的性价比还是很高的。
当哈希值分布不均匀时,数据分布也不会均衡。在哈希环与真实节点间,添加虚拟节点层,可以通过新的哈希函数,分散不均匀的数据。每个真实节点含有的虚拟节点数越多,数据分布便会越均衡,但同时也会消耗更多的内存与计算力。
虚拟节点带来的最大优点,是宕机时由所有节点共同分担流量缺口,这避免了可能产生的雪崩效应。同时,扩容的新节点也会分流所有节点的压力,这也提升了系统整体资源的利用率。
思考题
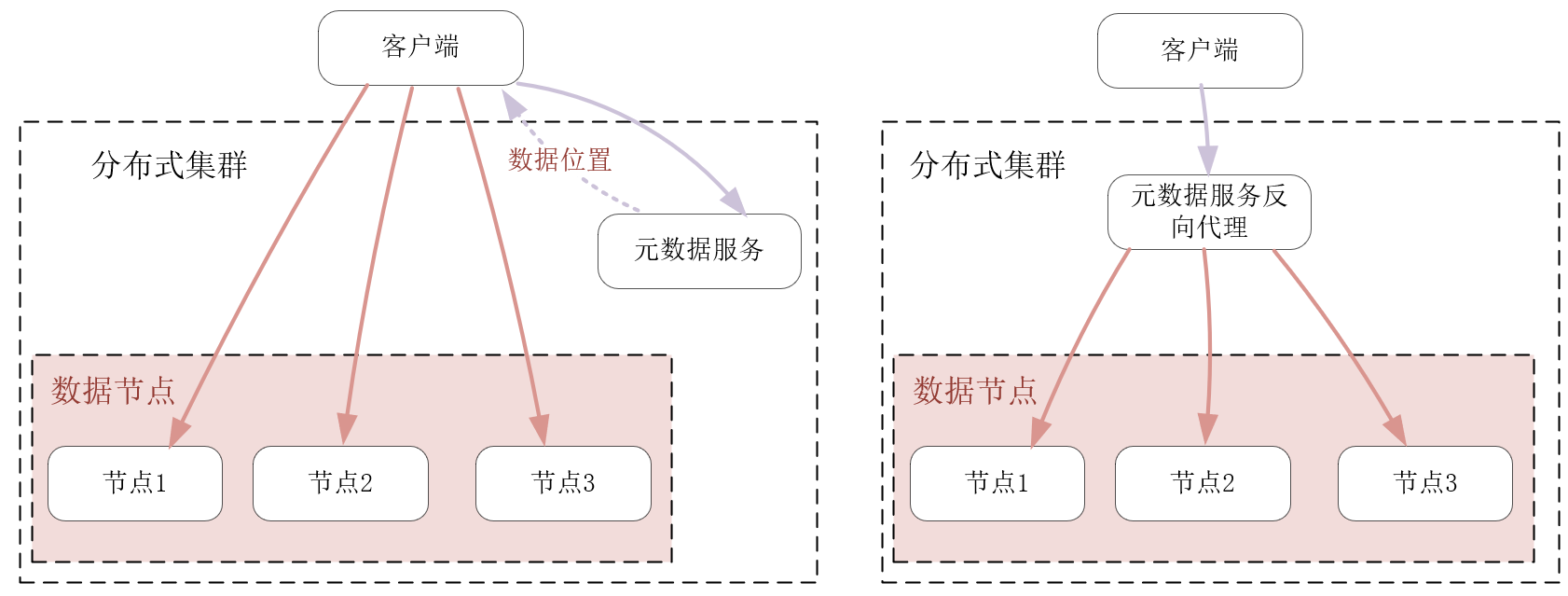
最后,留给你一道思考题。提升数据分布、访问的平衡性,并不是只有一致性哈希这一个方案。比如,我们将数据与节点的映射关系放在另一个服务中持久化存储,通过反向代理或者客户端SDK,在访问数据节点前,先从元数据服务中获取到数据的映射关系,再访问对应的节点,也是可以的,如下图所示:
你觉得上述方案与一致性哈希相比,有何优劣?各自适用的场景又是什么?欢迎你在留言区与大家一起探讨。
感谢阅读,如果你觉得这节课让你掌握了一致性哈希算法这个新工具,并能够用它提升分布式系统的运行效率,也欢迎把今天的内容分享给你的朋友。