123 lines
12 KiB
Markdown
123 lines
12 KiB
Markdown
# 17 | 时间和空间复杂度(下):如何使用六个法则进行复杂度分析?
|
||
|
||
你好,我是黄申,今天我们接着聊复杂度分析的实战。
|
||
|
||
上一讲,我从数学的角度出发,结合自身经验给你总结了几个分析复杂度的法则。但是在实际工作中我们会碰到很多复杂的问题,这个时候,正确地运用这些法则并不是件容易的事。今天,我就结合几个案例,教你一步步使用这几个法则。
|
||
|
||
## 案例分析一:广度优先搜索
|
||
|
||
在有关图遍历的专栏中,我介绍了单向广度优先和双向广度优先搜索。当时我提到了通常情况下,双向广度优先搜索性能更好。那么,我们应该如何从理论上分析,谁的效率更高呢?
|
||
|
||
首先我们来看单向广度优先搜索。我们先快速回顾一下搜索的主要步骤。
|
||
|
||
第一步,判断边界条件,时间和空间复杂度都是O(1)。
|
||
|
||
第二步,生成空的队列。常量级的CPU和内存操作,根据**主次分明法则**,时间和空间复杂度都是O(1)。
|
||
|
||
第三步,把搜索的起始结点放入队列queue和已访问结点的哈希集合visited,类似上一步,常量级操作,时间和空间复杂度都是O(1)。
|
||
|
||
第四步,也是最核心的步骤,包括了while和for的两个循环嵌套。
|
||
|
||
我们首先看时间复杂度。根据**四则运算法则**,时间复杂度是两个循环的次数相乘。对于嵌套在内的for循环,这个次数很好理解,和每个结点的直接连接点有关。如果要计算平均复杂度,我们就取直接连接点的平均数量,假设它为m。
|
||
|
||
现在的难题在于,第一个while循环次数是多少呢?我们考虑一下**齐头并进法则**,是否存在其他的因素来决定计算的次数?第一次的while循环,只有起始点一个。从起始点出发,会找到m个一度连接点,把它们放入队列,那么第二次while循环就是m次,依次类推,到第i次,那么总次数就是(m+m\*m+m\*m\*m+…+m^i)。这里我们假设被重复访问的结点不多,可以忽略不计。
|
||
|
||
在循环内部,所有操作都是常量级的,包括通过哈希集合判断是否找到终止结点。所以时间复杂度就是O(m+m\*m+m\*m\*m+…+m^i),取最高数量级m^i,最后可以简化成O(m^i),其中i是从起始点开始所走的边数。这就是除了m之外的第二个关键因素。
|
||
|
||
如果你觉得还是不太好理解,可以使用**一图千言法则**,我画了一张图来帮助你理解。
|
||
|
||
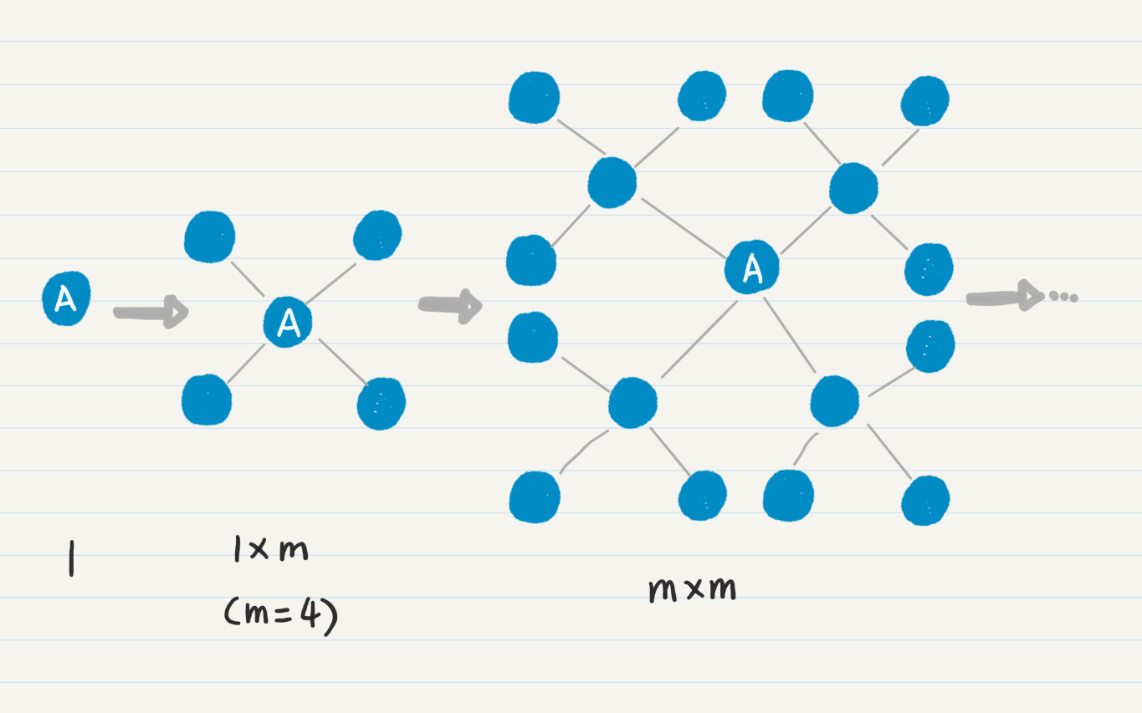
|
||
|
||
我们再来看这个步骤的空间复杂度。通过代码你应该可以看出来,只有queue和visited变量新增了数据,而图的结点本身没有发生改变。所以,考虑内存空间使用时,只需要考虑queue和visited的使用情况。两者都是在新发现一个结点时进行操作,因此新增的内存空间和被访问过的结点数成正比,同样为O(m^i)。
|
||
|
||
最后,这四步是平行的,所以我们只需要把这几个时间复杂度相加就行了。很明显前三步都是常量,只有最后一步是决定性因素,因此时间和空间复杂度都是O(m^i)。
|
||
|
||
我这里没有考虑图的生成,因为这步在单向搜索和双向搜索中是一样的,而且在实际项目中,我们也不会采用随机生成的方式。
|
||
|
||
接下来,我们来看看双向广度优先搜索。我刚才已经把单向的搜索过程分析得很透彻了,所以双向的复杂度你应该很容易就能得出来。但是,有两处关键点需要你注意。
|
||
|
||
第一个关键点是双向搜索所要走的边数。如果单向需要走i条边,那么双向是i/2。因此时间和空间复杂度都会变为O(2\*m^(i/2),简写为O(m^(i/2))。这里i/2中的2不能省去,因为它是在指数上,改变了数量级。仅从这点来看,双向比单向的复杂度低。
|
||
|
||
第二个关键点是双向搜索过程中,判断是否找到通路的方式。单向搜索只需要判断一个点是否存在集合中,每次只有O(1)的复杂度。而双向搜索需要比较两个集合是否存在交集,复杂度肯定要高于O(1)。
|
||
|
||
最常规的实现方法是,循环遍历其中一个集合A,看看A中的每个元素是不是出现在集合B中。假设两个集合中元素的数量都为n,那么循环n次,那么时间复杂度就为O(n)。基于这些,我们重新写一下双向广度优先搜索的时间复杂度。
|
||
|
||
假设我们分别从$a$点和$b$点出发。
|
||
|
||
* 从$a$点出发,找到m个一度连接点$a\_{1}$,时间复杂度O(m),然后查看$b$是否在这m个结点中,时间复杂度是O(1)。
|
||
* 然后从$b$点出发,找到m个一度连接点$b\_{1}$,时间复杂度O(m),然后查看$a$和$a\_{1}$是不是在$b$和$b\_{1}$中,时间复杂度是O(m+1),简写为O(m)。
|
||
* 从$a$点继续推进到第二度的结点$a\_{2}$,这个时候$a$、$a\_{1}$和$a\_{2}$的并集的数量已经有1+m+m^2,而$b$和$b\_{1}$的并集数量只有1+m。
|
||
|
||
因此,针对$b$和$b\_{1}$的集合进行循环更高效一些,时间复杂度是O(m)。
|
||
|
||
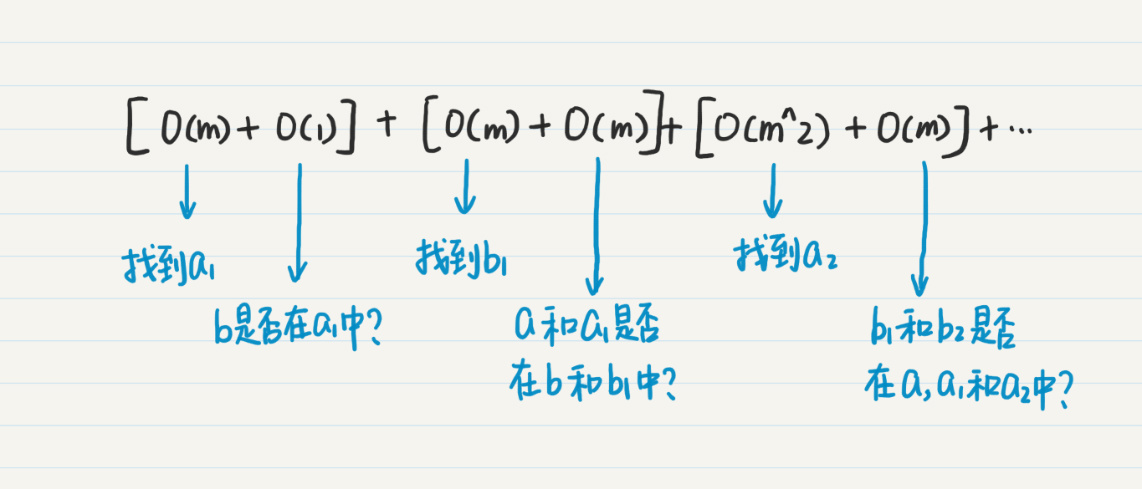
|
||
|
||
逐步递推下去,我们可以得到下面这个式子:
|
||
|
||
```
|
||
O(m) + O(1) + O(m) + O(m) + O(m^2) + O(m) ... + O(m^(i/2)) + O(m^(i/2)) = O(1) + O(4m) + O(4m^2) + ... + O(3m^(i/2))
|
||
|
||
```
|
||
|
||
虽然这个式子简化后仍然为O(m^(i/2)),但是我们可以通过这些推导的步骤了解整个算法运行的过程,以及对最终复杂度的影响。
|
||
|
||
最后比较单向广度搜索的复杂度O(m^i)和双向广度搜索的复杂度O(m^(i/2)),双向的方法更优。
|
||
|
||
不过,上面讨论的内容,都是假设每个点的直接相连点数量都很均匀,都是m个。如果数据不是均匀的呢?你可以利用排列组合的思想,想想看各种不同的情况。我想到了三种情况。
|
||
|
||
第一种情况,我用a=b来表示,也就是前面讨论的,不管从a和b哪个点出发,每个点的直接连接数量都是相当的。这个时候的最好、最坏和平均复杂度非常接近。
|
||
|
||
第二种情况,我用a<b来表示,表示从a点出发,每个点的直接连接数量远远小于从b点出发的那些。例如,从a点出发,2度之内所有的点都只有1、2个直接相连点,而从b点出发,2度之内的大部分点都有100个以上的直接相连点。
|
||
|
||
第三种情况和第二种类似,我用a>b表示,表示从b点出发,每个点的直接连接数量远远小于从a点出发的那些。
|
||
|
||
对于第二和第三种情况,双向搜索的最坏、最好和平均的复杂度是多少?还会是双向的方法更优吗?仔细分析一下各种情况,你就能回答第14讲的思考题了。
|
||
|
||
## 案例分析二:全文搜索
|
||
|
||
刚才的分析中,我们已经使用了6个复杂度分析法则中的5个,不过还没涉及最后一个时空互换。这个原则有自己的特殊性,我们需要通过牺牲空间复杂度来降低时间复杂度,或者反其道行之。
|
||
|
||
因此,在实际运用中,我们更多的是使用这个原则来指导和优化系统的设计。今天,我用搜索引擎的例子,来给你讲讲如何做到这一点。
|
||
|
||
搜索引擎你一定用得很多了,它最基本的也最重要的功能,就是根据你输入的关键词,查找指定的数据对象。这里,我以文本搜索为例。要查找某个关键词是不是出现在一篇文章里,最基本的处理方式有两种。
|
||
|
||
第一,把全文作为一个很长的字符串,把用户输入的关键词作为一个子串,那这个搜索问题就变成了**子串匹配的问题**。
|
||
|
||
假设字符串平均长度为n个字符,关键词平均长度为m个字符,使用最简单的暴力法,就是把代表全文的字符串的每个字符,和关键词字符串的每个字符两两相比,那么时间复杂度就是O(n\*m)。
|
||
|
||
第二,对全文进行分词,把全文切分成一个个有意义的词,那么这个搜索问题就变成了**把输入关键词和这些切分后的词进行匹配的问题**。
|
||
|
||
拉丁文分词比较简单,基本上就是根据各种分隔符来切分。而中文分词涉及很多算法,不过这不是我们讨论的重点,我们假设无论何种语言、何种分词方法,时间复杂度都是O(n),其中n为文章的长度。而在词的集合中查找输入的关键词,时间复杂度是O(m),m为词集合中元素的数量。
|
||
|
||
我们也可以先对词的集合排序,时间复杂度是O(m\*logm),然后使用二分查找,时间复杂度都只有O(logm)。如果文章很少改变,那么全文的分词和词的排序,基本上都属于一次性的开销,对于关键词查询来说,每次的时间复杂度都只有O(logm)。
|
||
|
||
无论使用上述哪种方法,看上去时间复杂度都不算太高,是吧?可是,别忘了,我们可是在海量的文章中查找信息,还需要考虑文章数量这个因素。假设文章数量是k,那么时间复杂度就变为O(k\*n),或者O(k\*logm),数量级一下子就增加了。
|
||
|
||
为了降低搜索引擎在查询时候的时间复杂度,我们要引入倒排索引(或逆向索引),这就是典型的牺牲空间来换取时间。如果你对倒排索引的概念不熟悉,我打个比方给你解释一下。
|
||
|
||
假设你是一个热爱读书的人,当你进入图书馆或书店的时候,怎样快速找到自己喜爱的书籍?没错,就是看书架上的标签。如果看到一个架子上标着“极客时间 - 数学专栏”,那么恭喜你,离程序员的数学书就不远了。而倒排索引做的就是“贴标签”的事情。
|
||
|
||
为了实现倒排索引,对于每篇文章我们都要先进行分词,然后将分好的词作为该篇的标签。让我们看看下面三篇样例文章和对应的分词,也就是标签。其中,分词之后,我也做了一些标准化的处理,例如全部转成小写、去掉时态等。
|
||
|
||

|
||
|
||
上面这个表格看上去并没有什么特别。好,体现“倒排”的时刻来了。我们转换一下,不再从文章的角度出发,而是从标签的角度出发来看问题。也就是说,从每个标签,我们能找到哪些文章?通过这样的思考,我们可以得到下面这张表。
|
||
|
||
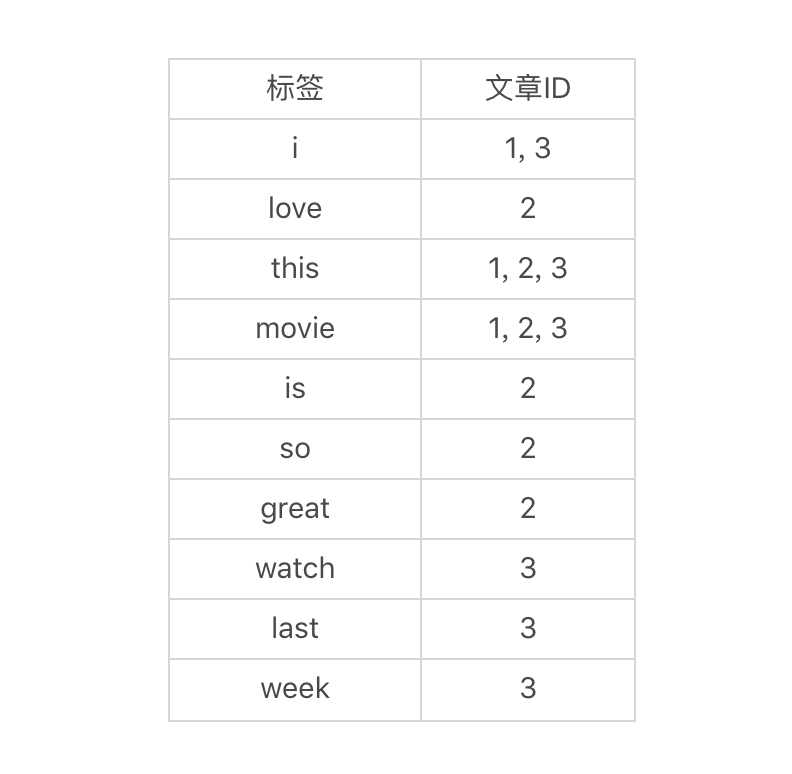
|
||
|
||
你看看,有了这张表格,想知道查找某个关键词在哪些文章中出现,是不是很容易呢?整个过程就像在哈希表中查找一样,时间复杂度只有O(1)了。当然,我们所要付出的成本就是倒排索引这张表。
|
||
|
||
假设有n个不同的单词,而每个单词所对应的文章平均数为m的话,那么这种索引的空间复杂度就是O(n\*m)。好在n和m通常不会太大,对内存和磁盘的消耗都是可以接受的。
|
||
|
||
## 小结
|
||
|
||
这一讲,我分析了两个复杂度的案例,并在其中穿插了6个法则的运用和讲解。随着项目经验的累积,你会发现复杂度分析是个很有趣,也很有成就感的事情。
|
||
|
||
更重要的是,它可以告诉我们哪些方法是可行的,哪些是不可行的,避免不必要的资源浪费。这里,资源浪费可能是硬件资源的浪费,也有可能是开发资源的浪费。这些法则中的数学思想并不高深,却可以帮我们有效地分析复杂度,运筹帷幄于帐中,决胜于千里之外。
|
||
|
||
## 思考题
|
||
|
||
在你日常的工作中,有没有经历过性能分析相关的项目?如果有,你都使用了哪些方法来分析问题的症结?
|
||
|
||
欢迎在留言区交作业,并写下你今天的学习笔记。你可以点击“请朋友读”,把今天的内容分享给你的好友,和他一起精进。
|
||
|