202 lines
15 KiB
Markdown
202 lines
15 KiB
Markdown
# 14 | 树的广度优先搜索(下):为什么双向广度优先搜索的效率更高?
|
||
|
||
你好,我是黄申。
|
||
|
||
上一讲,我们通过社交好友的关系,介绍了为什么需要广度优先策略,以及如何通过队列来实现它。有了广度优先搜索,我们就可以知道某个用户的一度、二度、三度等好友是谁。不过,在社交网络中,还有一个经常碰到的问题,那就是给定两个用户,如何确定他们之间的关系有多紧密?
|
||
|
||
最直接的方法是,使用这两人是几度好友,来衡量他们关系的紧密程度。今天,我就这个问题,来聊聊广度优先策略的一种扩展:双向广度优先搜索,以及这种策略在工程中的应用。
|
||
|
||
## 如何更高效地求出两个用户间的最短路径?
|
||
|
||
基本的做法是,从其中一个人出发,进行广度优先搜索,看看另一个人是否在其中。如果不幸的话,两个人相距六度,那么即使是广度优先搜索,同样要达到万亿级的数量。
|
||
|
||
那究竟该如何更高效地求得两个用户的最短路径呢?我们先看看,影响效率的问题在哪里?很显然,随着社会关系的度数增加,好友数量是呈指数级增长的。所以,如果我们可以控制这种指数级的增长,那么就可以控制潜在好友的数量,达到提升效率的目的。
|
||
|
||
如何控制这种增长呢?我这里介绍一种“**双向广度优先搜索**”。它巧妙地运用了两个方向的广度优先搜索,大幅降低了搜索的度数。现在我就带你看下,这个方法的核心思想。
|
||
|
||
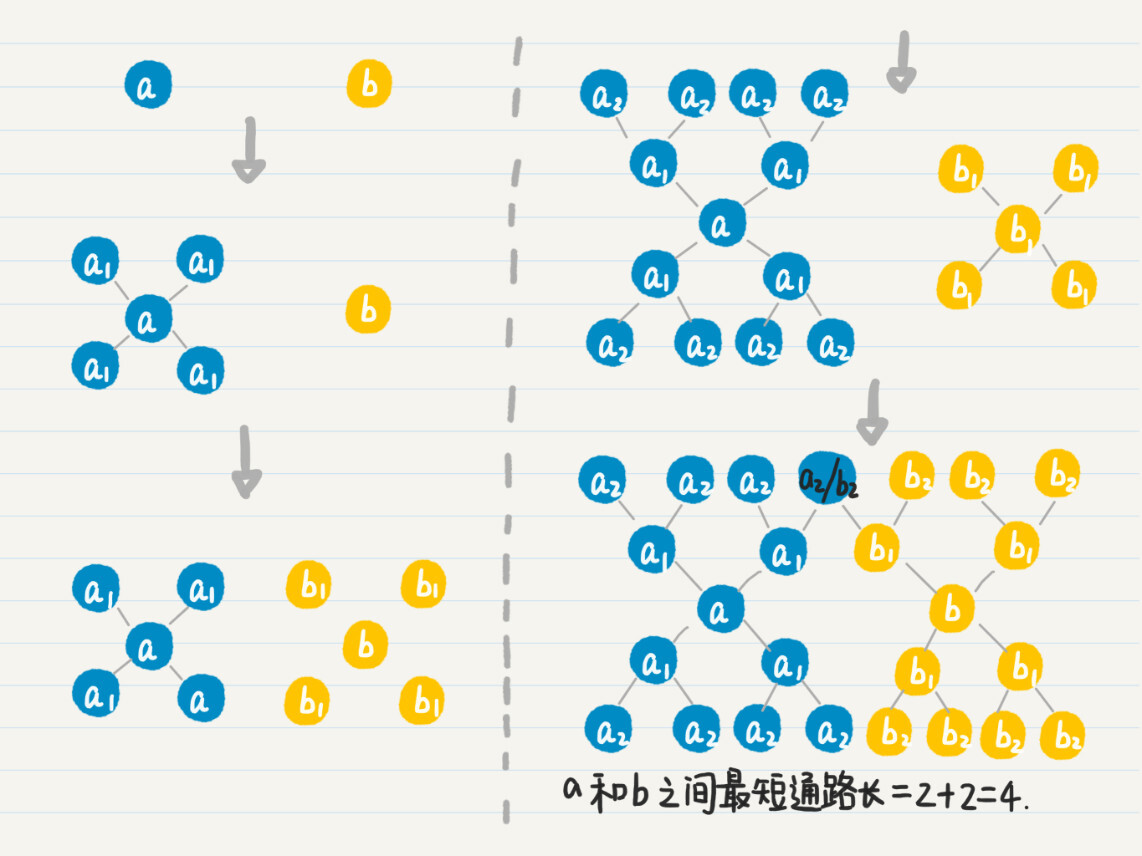
假设有两个人$a$、$b$。
|
||
|
||
* 我们首先从$a$出发,进行广度优先搜索,记录$a$的所有一度好友$a\_{1}$,然后看点$b$是否出现在集合$a\_{1}$中。
|
||
* 如果没有,就再从$b$出发,进行广度优先搜索,记录所有一度好友$b\_{1}$,然后看$a$和$a\_{1}$是否出现在$b$和$b\_{1}$的并集中。
|
||
* 如果没有,就回到$a$,继续从它出发的广度优先搜索,记录所有二度好友$a\_{2}$,然后看$b$和$b\_{1}$是否出现在$a$、$a\_{1}$和$a\_{2}$三者的并集中。
|
||
* 如果没有,就回到$b$,继续从它出发的广度优先搜索。
|
||
* 如此轮流下去,直到找到$a$的好友和$b$的好友的交集。
|
||
|
||
如果有交集,就表明这个交集里的点到$a$和$b$都是通路。
|
||
|
||
我们假设$c$在这个交集中,那么把$a$到$c$的通路长度和$b$到$c$的通路长度相加,得到的就是从$a$到$b$的最短通路长(这个命题可以用反证法证明),也就是两者为几度好友。这个过程有点复杂,我画了一张图帮助你来理解。
|
||
|
||
|
||
|
||
思路你应该都清楚了,现在我们来看看如何用代码来实现。
|
||
|
||
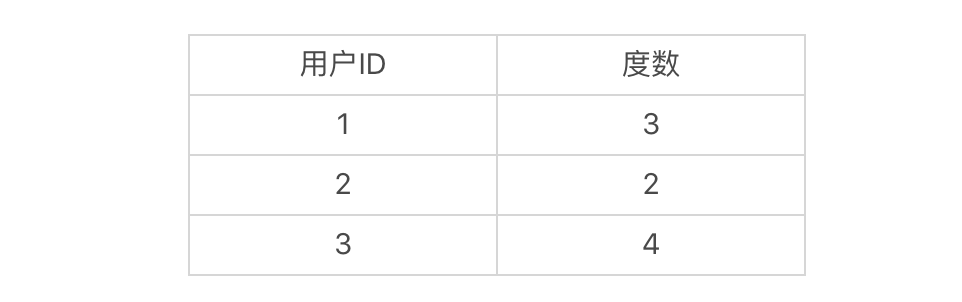
要想实现双向广度优先搜索,首先我们要把结点类Node稍作修改,增加一个变量degrees。这个变量是HashMap类型,用于存放从不同用户出发,到当前用户是第几度结点。比如说,当前结点是4,从结点1到结点4是3度,结点2到结点4是2度,结点3到结点4是4度,那么结点4的degrees变量存放的就是如下映射:
|
||
|
||
|
||
|
||
有了变量degrees,我们就能随时知道某个点和两个出发点各自相距多少。所以,在发现交集之后,根据交集中的点和两个出发点各自相距多少,就能很快地算出最短通路的长度。理解了这点之后,我们在原有的Node结点内增加degrees变量的定义和初始化。
|
||
|
||
```
|
||
public class Node {
|
||
......
|
||
public HashMap<Integer, Integer> degrees; // 存放从不同用户出发,当前用户结点是第几度
|
||
|
||
// 初始化结点
|
||
public Node(int id) {
|
||
......
|
||
degrees = new HashMap<>();
|
||
degrees.put(id, 0);
|
||
}
|
||
}
|
||
|
||
|
||
```
|
||
|
||
为了让双向广度优先搜索的代码可读性更好,我们可以先实现两个模块化的函数:getNextDegreeFriend和hasOverlap。函数getNextDegreeFriend是根据给定的队列,查找和起始点相距度数为指定值的所有好友。而函数hasOverlap用来判断两个集合是不是有交集。有了这些模块化的函数,双向广度优先搜索的代码就更直观了。
|
||
|
||
在函数一开始,我们先进行边界条件判断。
|
||
|
||
```
|
||
/**
|
||
* @Description: 通过双向广度优先搜索,查找两人之间最短通路的长度
|
||
* @param user_nodes-用户的结点;user_id_a-用户a的ID;user_id_b-用户b的ID
|
||
* @return void
|
||
*/
|
||
public static int bi_bfs(Node[] user_nodes, int user_id_a, int user_id_b) {
|
||
|
||
if (user_id_a > user_nodes.length || user_id_b > user_nodes.length) return -1; // 防止数组越界的异常
|
||
|
||
if (user_id_a == user_id_b) return 0; // 两个用户是同一人,直接返回0
|
||
|
||
```
|
||
|
||
由于同时从两个用户的结点出发,对于所有,有两条搜索的路径,我们都需要初始化两个用于广度优先搜索的队列,以及两个用于存放已经被访问结点的HashSet。
|
||
|
||
```
|
||
Queue<Integer> queue_a = new LinkedList<Integer>(); // 队列a,用于从用户a出发的广度优先搜索
|
||
Queue<Integer> queue_b = new LinkedList<Integer>(); // 队列b,用于从用户b出发的广度优先搜索
|
||
|
||
queue_a.offer(user_id_a); // 放入初始结点
|
||
HashSet<Integer> visited_a = new HashSet<>(); // 存放已经被访问过的结点,防止回路
|
||
visited_a.add(user_id_a);
|
||
|
||
queue_b.offer(user_id_b); // 放入初始结点
|
||
HashSet<Integer> visited_b = new HashSet<>(); // 存放已经被访问过的结点,防止回路
|
||
visited_b.add(user_id_b);
|
||
|
||
|
||
```
|
||
|
||
接下来要做的是,从两个结点出发,沿着各自的方向,每次广度优先搜索一度,并查找是不是存在重叠的好友。
|
||
|
||
```
|
||
int degree_a = 0, degree_b = 0, max_degree = 20; // max_degree的设置,防止两者之间不存在通路的情况
|
||
|
||
while ((degree_a + degree_b) < max_degree) {
|
||
degree_a ++;
|
||
getNextDegreeFriend(user_id_a, user_nodes, queue_a, visited_a, degree_a);
|
||
// 沿着a出发的方向,继续广度优先搜索degree + 1的好友
|
||
if (hasOverlap(visited_a, visited_b)) return (degree_a + degree_b);
|
||
// 判断到目前为止,被发现的a的好友,和被发现的b的好友,两个集合是否存在交集
|
||
|
||
degree_b ++;
|
||
getNextDegreeFriend(user_id_b, user_nodes, queue_b, visited_b, degree_b);
|
||
// 沿着b出发的方向,继续广度优先搜索degree + 1的好友
|
||
if (hasOverlap(visited_a, visited_b)) return (degree_a + degree_b);
|
||
// 判断到目前为止,被发现的a的好友,和被发现的b的好友,两个集合是否存在交集
|
||
|
||
}
|
||
|
||
return -1;
|
||
// 广度优先搜索超过max_degree之后,仍然没有发现a和b的重叠,认为没有通路
|
||
|
||
}
|
||
|
||
```
|
||
|
||
你可以同时实现单向广度优先搜索和双向广度优先搜索,然后通过实验来比较两者的执行时间,看看哪个更短。如果实验的数据量足够大(比如说结点在1万以上,边在5万以上),你应该能发现,**双向的方法对时间和内存的消耗都更少**。
|
||
|
||
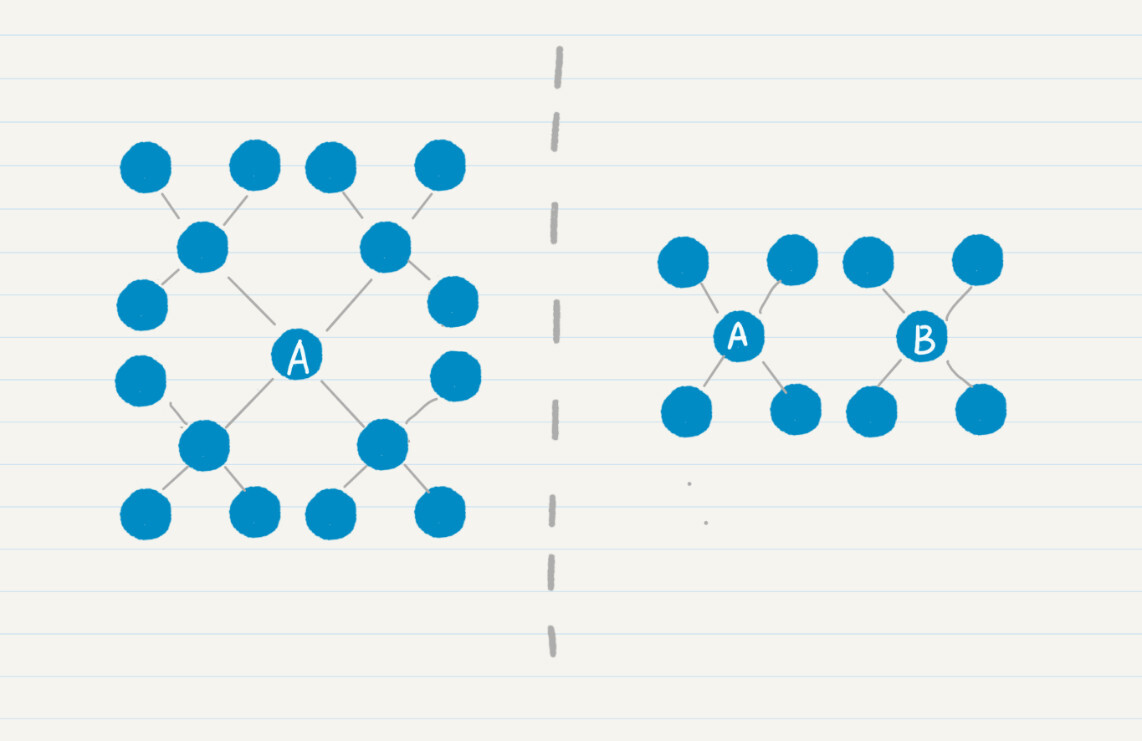
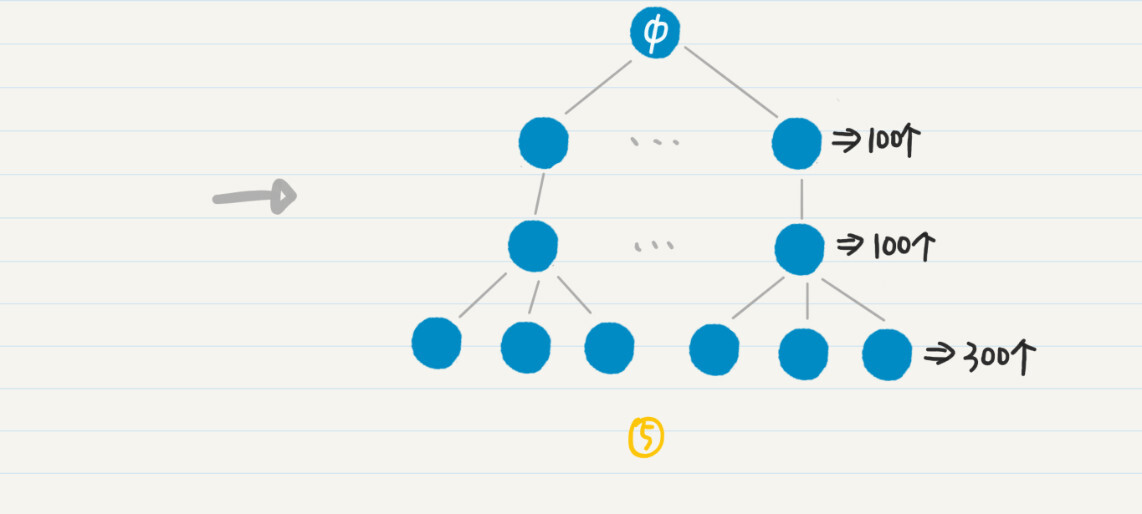
为什么双向搜索的效率更高呢?我以平均好友度数为4,给你举例讲解。
|
||
|
||
左边的图表示从结点$a$单向搜索走2步,右边的图表示分别从结点$a$和$b$双向搜索各走1步。很明显,左边的结点有16个,明显多于右边的8个结点。而且,随着每人认识的好友数、搜索路径的增加,这种差距会更加明显。
|
||
|
||
|
||
|
||
我们假设每个地球人平均认识100个人,如果两个人相距六度,单向广度优先搜索要遍历100^6=1万亿左右的人。如果是双向广度优先搜索,那么两边各自搜索的人只有100^3=100万。
|
||
|
||
当然,你可能会说,单向广度优先搜索之后查找匹配用户的开销更小啊。的确如此,假设我们要知道结点$a$和$b$之间的最短路径,单向搜索意味着要在$a$的1万亿个好友中查找$b$。如果采用双向搜索的策略,从结点$a$和$b$出发进行广度优先搜索,每个方向会产生100万的好友,那么需要比较这两组100万的好友是否有交集。
|
||
|
||
假设我们使用哈希表来存储$a$的1万亿个好友,并把搜索$b$是否存在其中的耗时记作x,而把判断两组100万好友是否有交集的耗时记为y,那么通常x<y。
|
||
|
||
不过,综合考虑广度优先搜索出来的好友数量,双向广度优先搜索还是更有效。为什么这么说呢?稍后介绍算法复杂度的概念和衡量方法时,我会具体来分析这个例子。
|
||
|
||
广度优先搜索的应用场景有很多,下面我来说说这种策略的一个应用。
|
||
|
||
## 如何实现更有效地嵌套型聚合?
|
||
|
||
广度优先策略可以帮助我们大幅优化数据分析中的聚合操作。聚合是数据分析中一个很常见的操作,它会根据一定的条件把记录聚集成不同的分组,以便我们统计每个分组里的信息。目前,SQL语言中的GROUP BY语句,Python和Spark语言中data frame的groupby函数,Solr的facet查询和ElasticSearch的aggregation查询,都可以实现聚合的功能。
|
||
|
||
我们可以嵌套使用不同的聚合,获得层级型的统计结果。但是,实际上,针对一个规模超大的数据集,聚合的嵌套可能会导致性能严重下降。这里我来谈谈如何利用广度优先的策略,对这个问题进行优化。
|
||
|
||
首先,我用一个具体的例子来给你讲讲,什么是多级嵌套的聚合,以及为什么它会产生严重的性能问题。
|
||
|
||
这里我列举了一个数据表,它描述了一个社交网络中,每个人的职业经历。字段包括项目的ID、用户ID、公司ID和同事的IDs。
|
||
|
||

|
||
|
||
对于这张表,我们可以进行三层嵌套的聚集。第一级是根据用户ID来聚,获取每位用户一共参与了多少项目。第二级是根据公司ID来聚,获取每位用户在每家公司参与了多少项目。第三级根据同事ID来聚,获取每位用户在每家公司,和每位同事共同参与了多少项目。最终结果应该是类似下面这样的:
|
||
|
||
```
|
||
用户u88,总共50个项目(包括在公司c42中的10个,c26中的8个...)
|
||
在公司c42中,参与10个项目(包括和u120共事的4个,和u99共事的3个...)
|
||
和u120共同参与4个项目
|
||
和u99共同参与3个项目
|
||
和u72共同参与3个项目
|
||
在公司c26中,参与了8个项目
|
||
和u145共同参与5个项目
|
||
和u128共同参与3个项目
|
||
(用户u88在其他公司的项目...)
|
||
|
||
用户u66,总共47个项目
|
||
在公司c28中,参与了16个项目
|
||
和u65共同参与了5个项目
|
||
(用户u66的剩余数据...)
|
||
...
|
||
(其他用户的数据...)
|
||
|
||
```
|
||
|
||
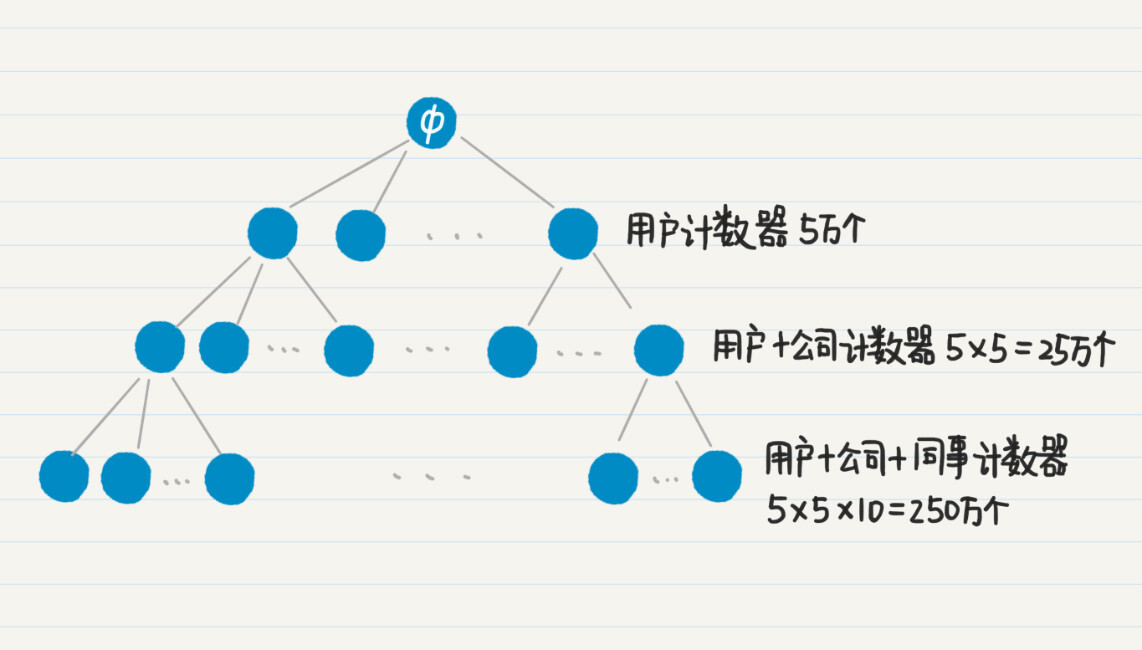
为了实现这种嵌套式的聚合统计,你会怎么来设计呢?看起来挺复杂的,其实我们可以用最简单的排列的思想,分别为“每个用户”“每个用户+每个公司”“每个用户+每个公司+每位同事”,生成很多很多的计数器。可是,如果用户的数量非常大,那么这个“很多”就会成为一个可怕的数字。
|
||
|
||
我们假设这个社交网有5万用户,每位用户平均在5家公司工作过,而用户在每家公司平均有10名共事的同事,那么针对用户的计数器有5万个,针对“每个用户+每个公司”的计数器有25万个,而到了“每个用户+每个公司+每位同事”的计数器,就已经达到250万个了,三个层级总共需要280万计数器。
|
||
|
||
|
||
|
||
我们假设一个计数器是4个字节,那么280万个计数器就需要消耗超过10M的内存。对于高并发、低延迟的实时性服务,如果每个请求都要消耗10M内存,很容易就导致服务器崩溃。另外,实时性的服务,往往只需要前若干个结果就足以满足需求了。在这种情况下,完全基于排列的设计就有优化的空间了。
|
||
|
||
从刚才那张图中,其实我们就能想到一些优化的思路。
|
||
|
||
对于只需要返回前若干结果的应用场景,我们可以对图中的树状结构进行剪枝,去掉绝大部分不需要的结点和边,这样就能节省大量的内存和CPU计算。
|
||
|
||
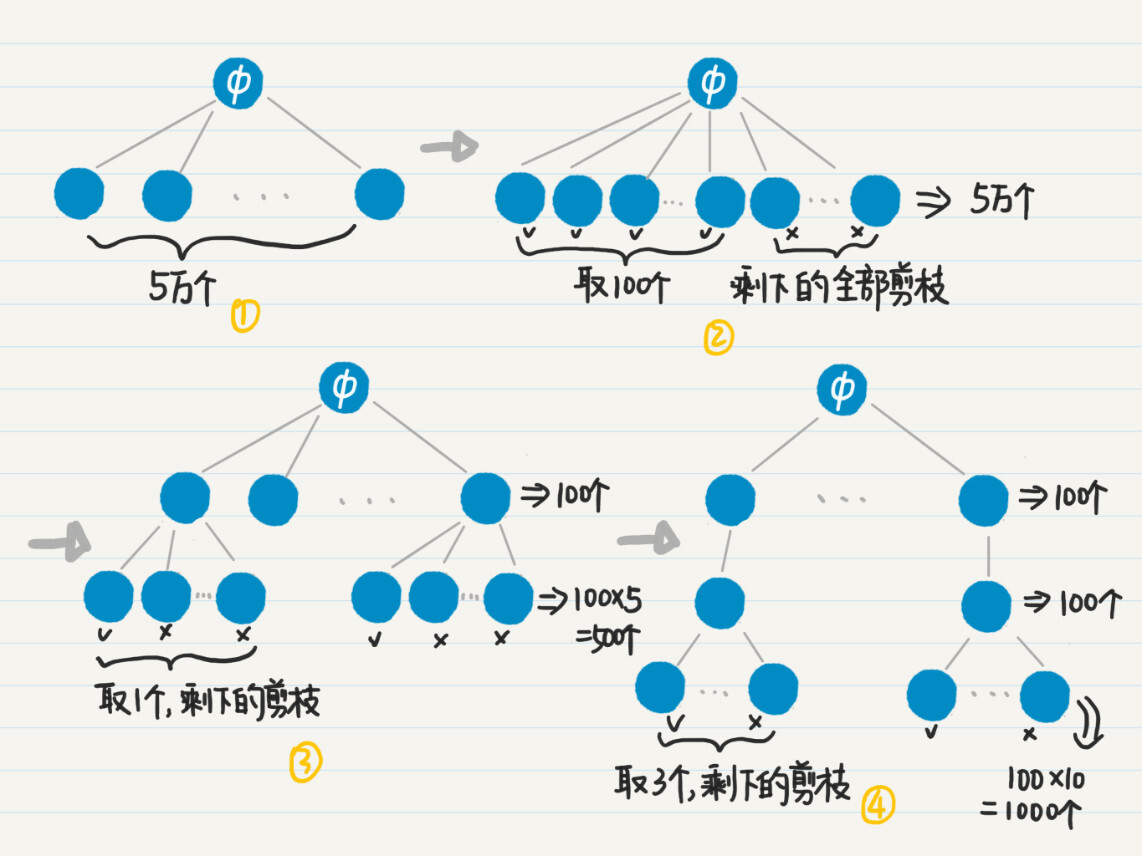
比如,如果我们只需要返回前100个参与项目最多的用户,那么就没有必要按照深度优先的策略,去扩展树中高度为2和3的结点了,而是应该使用广度优先策略,首先找出所有高度为1的结点,根据项目数量进行排序,然后只取出前100个,把计数器的数量从5万个一下子降到100个。
|
||
|
||
以此类推,我们还可以控制高度为2和3的结点之数量。如果我们只要看前100位用户,每位用户只看排名第一的公司,而每家公司只看合作最多的3名同事,那么最终计数器数量就只有50000+100x5+100x1x10=51500。只有文字还是不太好懂,我画了一张图,帮你理解这个过程。
|
||
|
||
|
||
|
||
如果一个项目用到排列组合的思想,我们需要在程序里使用大量的变量,来保存数据或者进行计算,这会导致内存和CPU使用量的急剧增加。在允许的情况下,我们可以考虑使用广度优先策略,对排列组合所生成的树进行优化。这样,我们就可以有效地缩减树中靠近根的结点数量,避免之后树的爆炸性生长。
|
||
|
||
## 小结
|
||
|
||
广度优先搜索,相对于深度优先搜索,没有函数的嵌套调用和回溯操作,所以运行速度比较快。但是,随着搜索过程的进行,广度优先需要在队列中存放新遇到的所有结点,因此占用的存储空间通常比深度优先搜索多。
|
||
|
||
相比之下,深度优先搜索法只保留用于回溯的结点,而扩展完的结点会从栈中弹出并被删除。所以深度优先搜索占用空间相对较少。不过,深度优先搜索的速度比较慢,而并不适合查找结点之间的最短路径这类的应用。
|
||
|
||

|
||
|
||
## 思考题
|
||
|
||
今天所说的双向广度优先比单向广度优先更高效,其实是要基于一个前提条件的。你能否说出,在什么情况下,单向广度优先更高效呢?针对这种情况,又该如何优化双向广度优先呢?
|
||
|
||
欢迎在留言区交作业,并写下你今天的学习笔记。你可以点击“请朋友读”,把今天的内容分享给你的好友,和他一起精进。
|
||
|