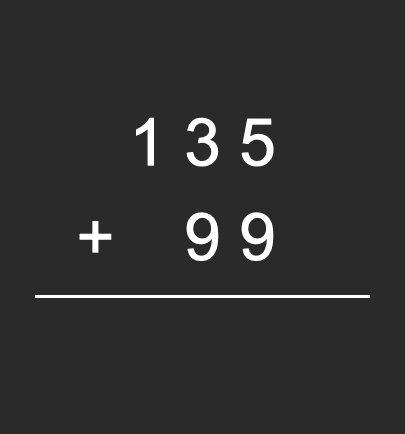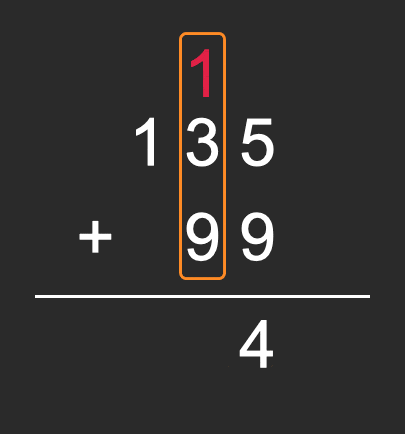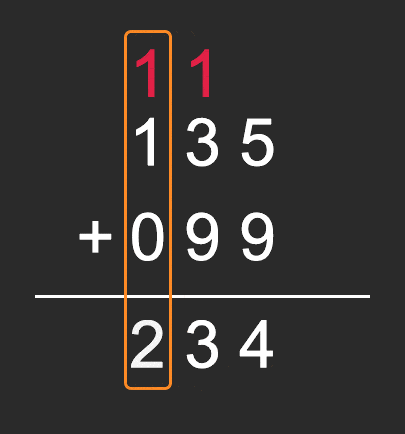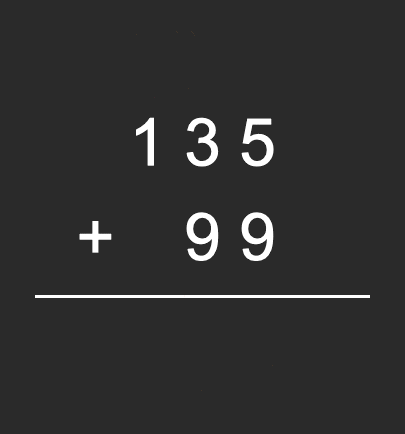30 KiB
04 | 实战:构建一个Kotlin版本的四则运算计算器
你好,我是朱涛。
前面几节课,我们学了不少Kotlin的语法,也算是对Kotlin有了一个基本认识。不过,单纯只认识Kotlin是远远不够的,我们还要会用Kotlin。当遇到一个具体问题的时候,我们得能用Kotlin来解决这个问题。换句话说,就是要实战。在实战的过程中,我们对Kotlin的理解也会进一步加深。
那么这节课,我们就把前面的知识点串联起来,一起做一个Kotlin版本的计算器。为了便于理解,我会以循序渐进的方式来编写这个计算器程序,由简单到复杂。你在这个由易到难的实操过程中,可以实际体会到Kotlin的代码实现思路以及编码方式的变化,进而也就能更好地掌握和运用前面所学的基础语法,以及与面向对象相关的知识点。
这个计算器程序大致会分为三个版本:
- 计算器1.0,实现两个整数的“加减乘除”,对输入数据有严格要求。
- 计算器2.0,对输入数据无严格要求,融入面向对象的编程思想。
- 计算器3.0,支持“大数的加法”,增加单元测试。
现在,我们就开始实战吧。
创建Kotlin工程
如果你之前没有使用过IntelliJ或Android Studio,你可能还不知道怎么创建一个工程。别担心,这个过程其实很简单,它分为以下几个步骤。
- 第一步:选择菜单“File -> New -> Project”。
- 第二步:选中菜单左边的“Gradle”,然后在右边勾选“Java 和 Kotlin/JVM”,最后点击右下角的“Next”。
- 第三步:给工程取一个你喜欢的名字,我们这里就用Calculator。GroupId这个地方一般使用倒过来的域名,这里根据你的实际情况填写即可。默认情况下,IDE会自动帮你设置成“org.example”,所以你不去改动它也没问题。最后,我们点击Finish,工程就创建成功了!
- 第四步:等待工程配置完成。**如果你是第一次创建Kotlin工程,点击Finish以后,你可能需要等待一段时间,IDE需要下载Gradle,然后用Gradle下载工程所需的依赖。**当你在IDE当中能看到这样的工程结构时,这个工程就算配置完成了。
导入初始化工程
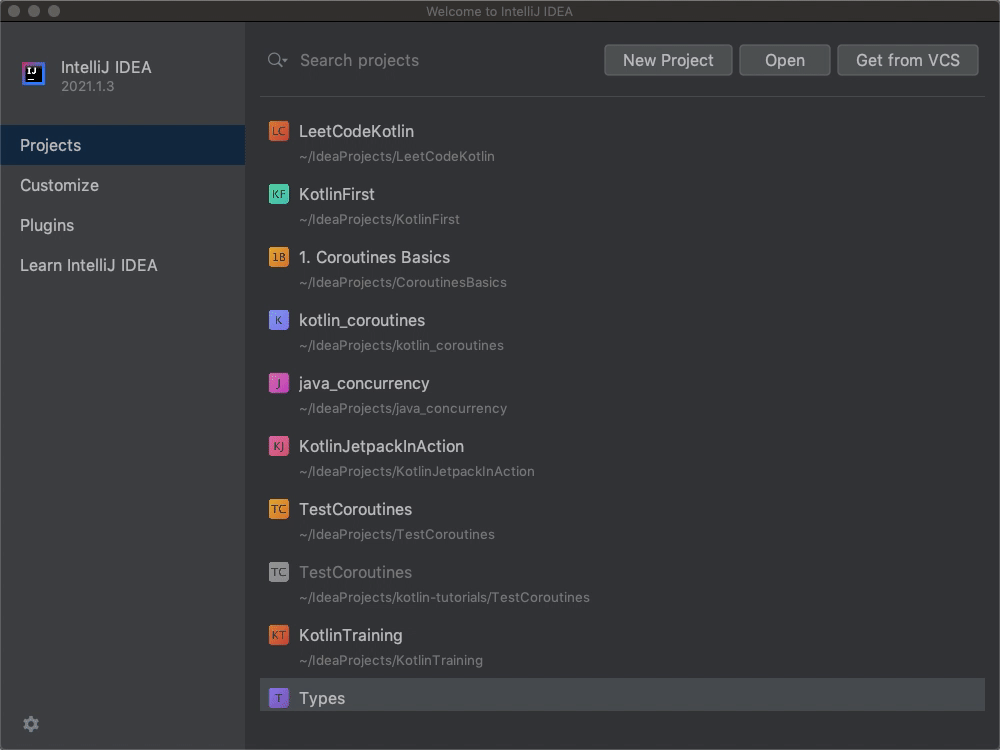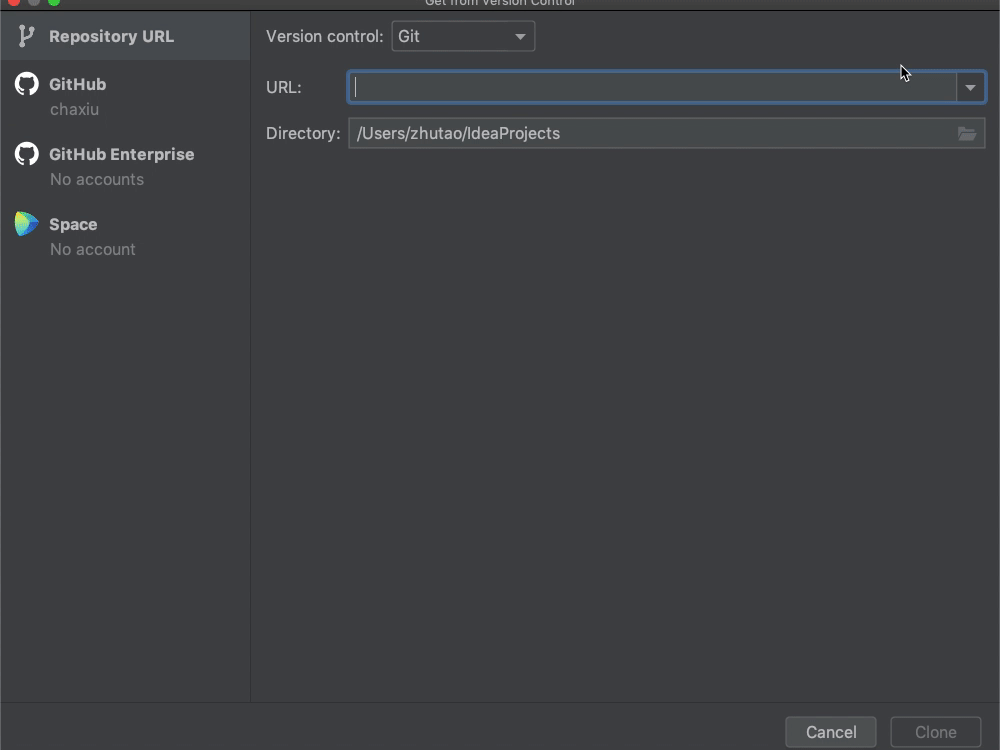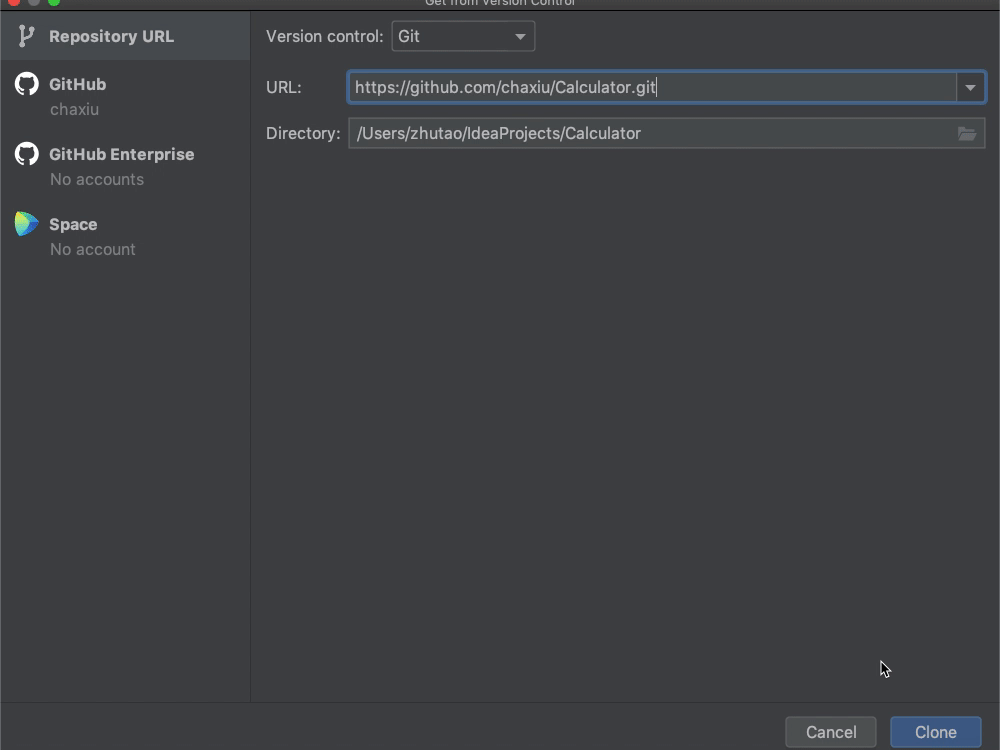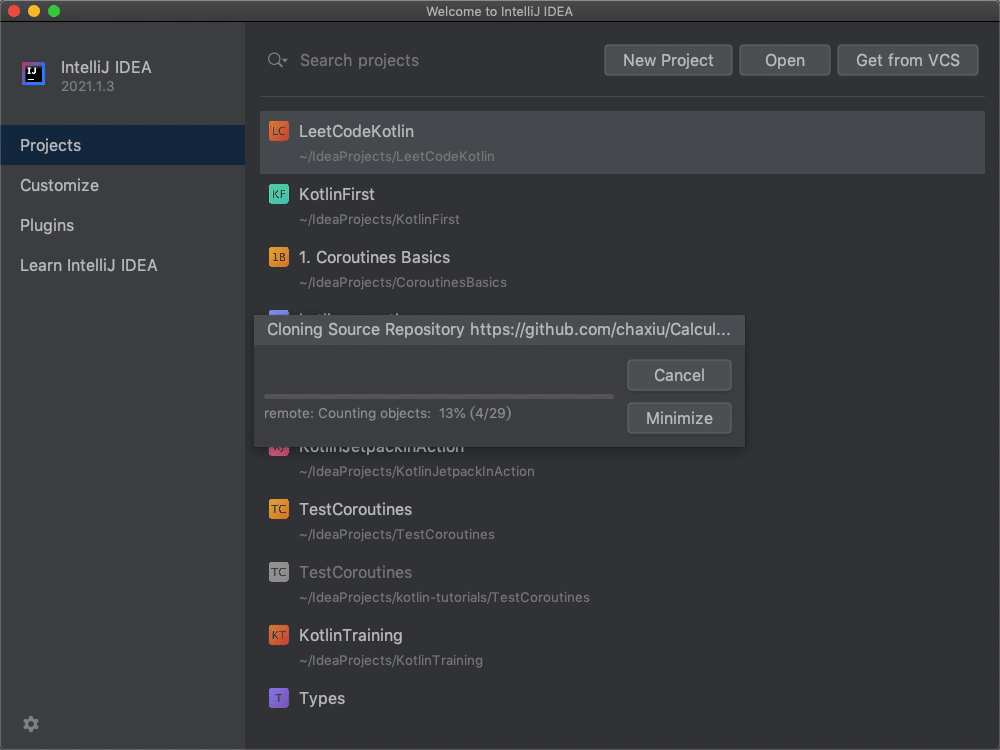
其实,你只需要知道如何创建一个Kotlin工程就行了,也没必要真的跟着我一步步操作。课程配套的源代码已经在GitHub开源,你可以将其下载下来并切换到start分支,这样就可以跟着课程一步步实现计算器的三个版本了。
**具体做法是这样的:**打开IntelliJ,点击“Get from VCS”按钮,接着在弹出的窗口中,填入我们的GitHub URL“https://github.com/chaxiu/Calculator.git”,然后点击右下角的Clone按钮即可。
等代码下载完成以后,IDE会问你是否要打开此工程,我们选择打开。这样,我们的计算器工程就算导入进来了。
最后,我们还需要将工程改为初始化状态,借助Git我们可以非常方便地实现:
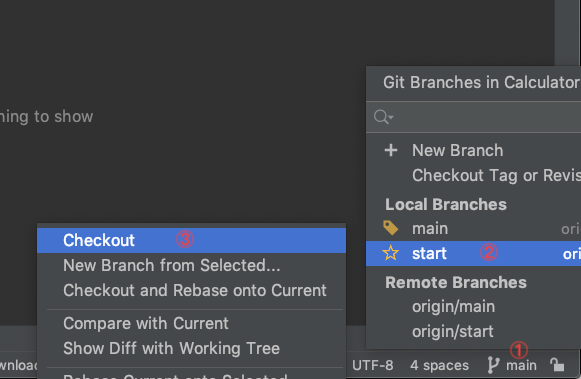
- 在IntelliJ的右下角,找到main按钮并且点击;
- 在弹出的菜单中,点击start分支;
- 最后,点击Checkout,代表将当前代码切换到初始状态。
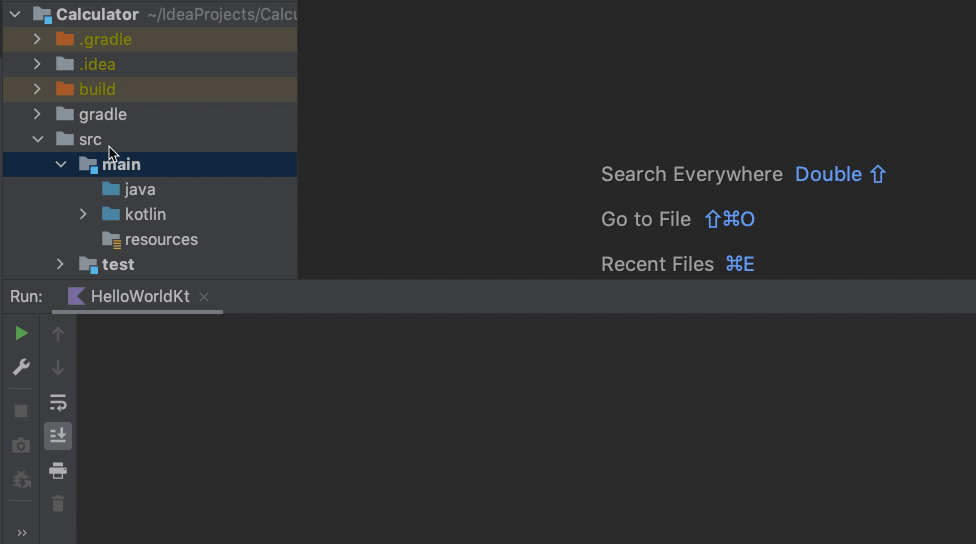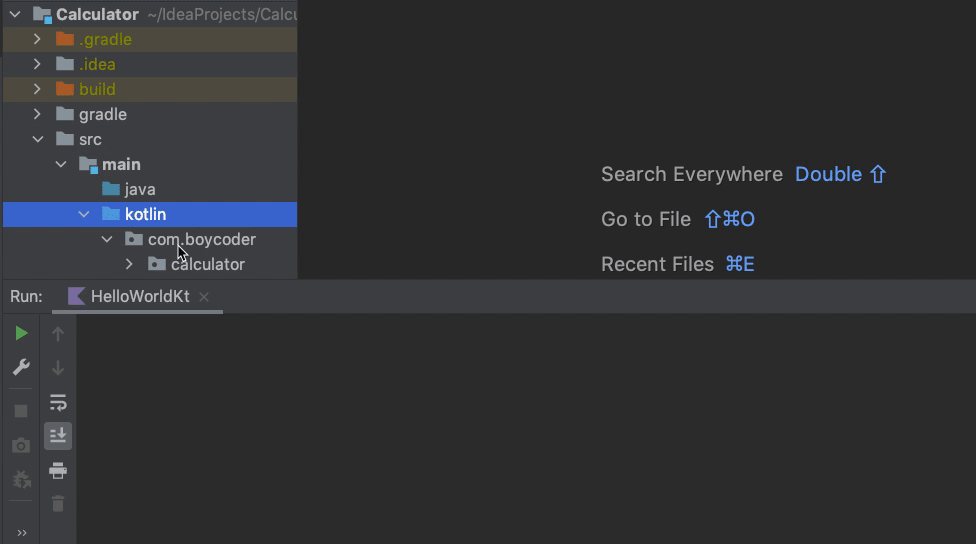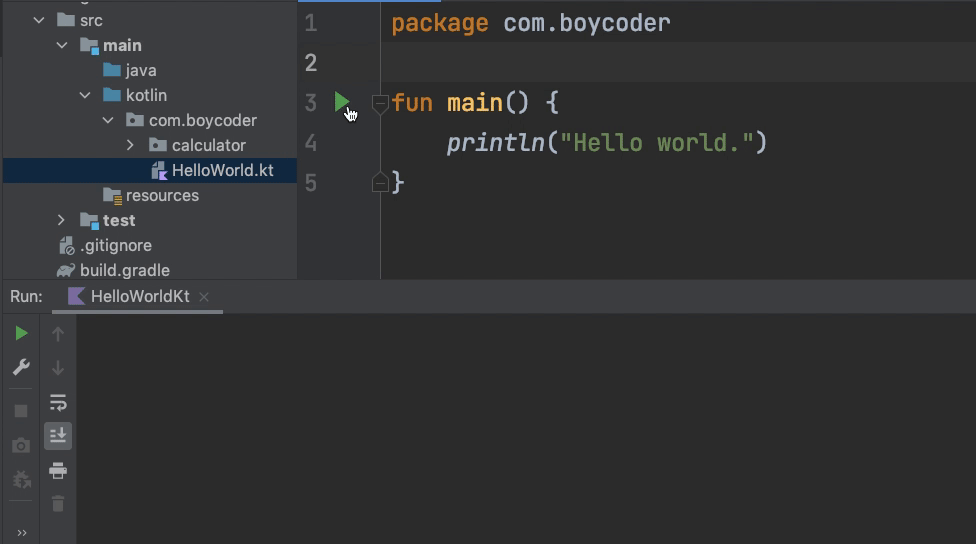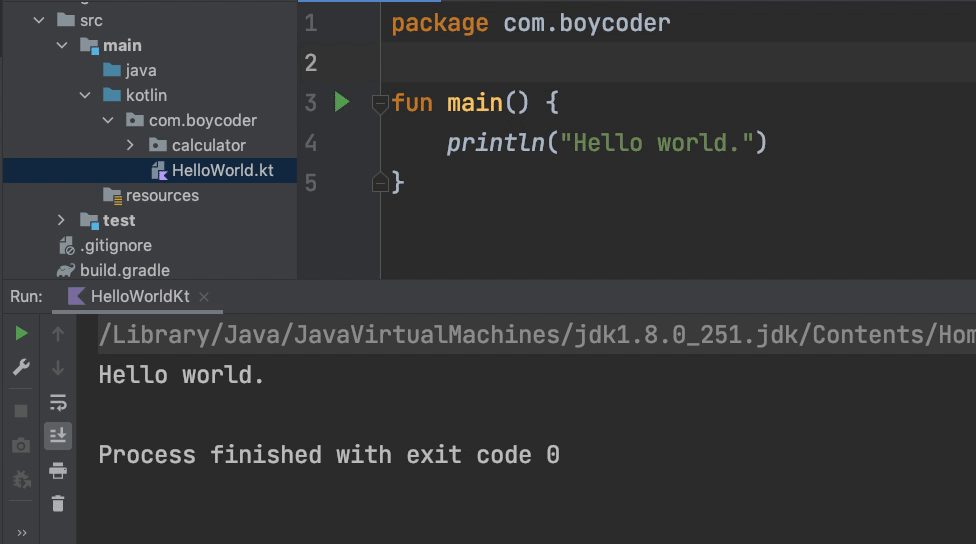
这样,我们就完成了整个工程的初始化配置了。为了测试我们的开发环境是否已经配置好,我们可以打开工程里的HelloWorld文件,运行一下,看看程序是否正常执行。
如果你也能在工程当中看见控制台输出“Hello world.”,说明你的开发环境已经完全没问题了。接下来,就让我们一起用Kotlin完成计算器的1.0版本吧!
计算器1.0
第一个版本的计算器,它的功能非常简单,你可以看看下面的动图演示。
我们大致列举一下这个计算器的功能需求:
- 交互式界面,输入算式,按下回车,程序就会帮我们计算出结果;
- 数字与字符之间要求有空格,“1 + 1”是可以的,“1+1”则不行;
- 输入exit,按下回车,程序就会退出;
- 支持“加减乘除”,四种运算,仅支持两个数的运算。
搞清楚功能需求以后,我们就可以开始写代码了。
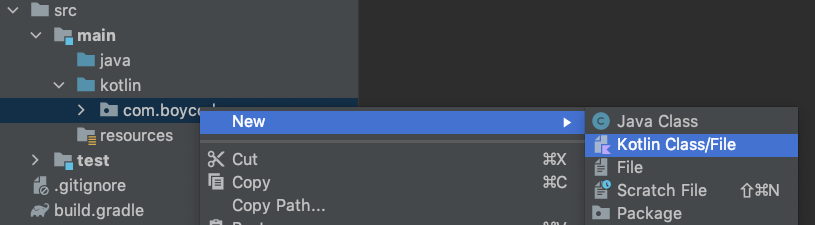
首先,我们要创建一个Kotlin源代码文件:在Kotlin文件夹下,点击右键,选择“New -> Kotlin Class/File”,然后填写文件名字即可,这里我们创建一个名为Calculator的Kotlin文件。
由于我们的程序要和命令进行交互,根据不同的命令来做出不同的行为,因此,我们的程序需要有一个 while循环的逻辑,在循环当中,还要读取命令行的输入,然后根据输入的结果来判断执行逻辑。我们可以将整个程序分为以下几个步骤:
- 初始化,打印提示信息;
- 第一步,读取输入命令;
- 第二步,判断命令是不是exit,如果用户输入的是“exit”则直接退出程序;
- 第三步,解析算式,分解出“数字”与“操作符”:“1”“+”“2”;
- 第四步,根据操作符类型,算出结果:3;
- 第五步,输出结果:1 + 2 = 3;
- 第六步,进入下一个while循环。
fun main() {
while(true) {
// 初始化,打印提示信息
println("请输入标准的算式,并且按回车; \n" +
"比如:1 + 1,注意符合与数字之间要有空格。\n" +
"输入exit,退出程序。")
// 第一步,读取输入命令;
var input = readLine()
if (input == null) continue
// 第二步,判断命令是不是exit,如果是则直接退出程序;
if (input == "exit") exitProcess(0)
// 第三步,解析算式,分解出“数字”与“操作符”:“1”“+”“2”;
var inputList = input.split(" ")
// 第四步,根据操作符类型,算出结果:3;
var result = calculate(inputList)
// 第五步,输出结果:1 + 2 = 3;
if (result == null) {
println("输入格式不对")
continue
} else {
println("$input = $result")
}
// 第六步,进入下一个while循环。
}
}
// 具体计算逻辑
private fun calculate(inputList: List<String>): Int? {
if (inputList.size != 3) return null
// 第七步,取出数字和操作符
var left = inputList.get(0).toInt()
var operation = inputList.get(1)
var right = inputList.get(2).toInt()
// 第八步,根据操作符的类型,执行计算
when(operation) {
"+" -> return left + right
"-" -> return left - right
"*" -> return left * right
"/" -> return left / right
else -> return null
}
}
上面的代码非常简单直白,即使你没有任何编程经验,应该也能够理解。它也非常符合人的编程直觉。
不过,站在Kotlin的角度上看,以上的代码其实是有不少问题的,让我们通过一个图来对比着看:
- 箭头①,表示程序中的“提示信息”应该使用Kotlin的“三引号”的原始字符串,这样的话,我们可以省去繁琐的“\n和+”,并且所见即所得;
- 箭头②,表示读取输入命令后,我们可以直接使用Elvis表达式,两行代码就会变成一行;
- 箭头③,表示程序中所有的var都应该改为val,我在第1讲中说过,在Kotlin当中,我们应该优先使用val,尽量避免使用可变的变量。
- 箭头④,表示inputList.get(i)可以改为inputList[i],这是因为Kotlin统一了数组和集合的元素访问操作,我们再也不用担心弄混了。
- 箭头⑤,表示了两点。首先,我们可以将return放到when表达式的前面,这样就省得我们每个分支都写一遍return。另外,当我们使用when表达式的时候,应该尽量结合“枚举”或者“密封类”来使用。为此,我们可以为“加减乘除”四个操作符创建一个枚举类。这样,when表达式的分支会自动判定完备,而不需要else分支了。
那么经过调整,最终的源代码应该是这样的:
val help = """
--------------------------------------
使用说明:
1. 输入 1 + 1,按回车,即可使用计算器;
2. 注意:数字与符号之间要有空格;
3. 想要退出程序,请输入:exit
--------------------------------------""".trimIndent()
fun main() {
while (true) {
println(help)
val input = readLine() ?: continue
if (input == "exit") exitProcess(0)
val inputList = input.split(" ")
val result = calculate(inputList)
if (result == null) {
println("输入格式不对")
continue
} else {
println("$input = $result")
}
}
}
private fun calculate(inputList: List<String>): Int? {
if (inputList.size != 3) return null
val left = inputList[0].toInt()
// ①
// ↓
val operation = Operation.valueOf(inputList[1])
val right = inputList[2].toInt()
return when (operation) {
Operation.ADD -> left + right
Operation.MINUS -> left - right
Operation.MULTI -> left * right
Operation.DIVI -> left / right
}
}
enum class Operation(val value: String) {
ADD("+"),
MINUS("-"),
MULTI("*"),
DIVI("/")
}
好,我们的计算器1.0版本,到这里就算是完成了。
如果你跟随着我,一起来实现了这个简单的计算器,那么你在这个实操过程中就可以体会到,Kotlin编程与传统的Java/C之间确实是存在着一定的差别的。
**想要学会Kotlin语法其实不难,但要写出优雅的Kotlin代码,却不是一件容易的事情。**我们唯一能做的,就是多写Kotlin代码,同时多看优秀的Kotlin代码,以及多思考改进自己已有的代码。
不过,代码中注释①处其实还有一些问题,接着让我们进入第二个版本的开发吧!
计算器2.0
在2.0版本中,我们会分成两个阶段:
- 第一个阶段,融入面向对象的思想。1.0版本中,我们只写了两个函数,一个是main()函数,另一个是calculate()函数。虽然这样的设计非常直观且便于理解,但却不太符合我们工程界的思维习惯。我们应该将程序封装到一个类当中,并且尽量让每个函数的功能划分清楚,保持每个函数尽量简单。
- 第二个阶段,兼容输入格式。1.0版本中,我们对输入有严格的要求,数字和符号之间必须有空格,否则我们的算式解析会出错。在2.0版本中,我们尝试兼容不同的输入格式,不管数字和符号之间有没有空格,我们都要能成功执行。
让我们一步步来,首先是融入面向对象的思想。
第一阶段:融入面向对象思想
具体做法其实也很简单,我们可以将前面定义的两个函数收拢到一个类当中去,比如“CalculatorV2”:
class CalculatorV2 {
fun start() {}
fun calculate(input: String): Int? {}
}
可以看到,在这个CalculatorV2类当中有两个方法,start() 用于启动我们的计算器程序,监听控制台的文本输入;calculate(input) 用于接收输入文本,计算出算式的结果,然后返回一个可为空的整型,当输入不合法的时候会返回null。
这样,我们的计算器作为一个整体已经是一个对象了,我们可以很方便地在main()函数当中,创建一个实例,并且调用它的start()函数。这样一来,我们的计算器也就可以充分发挥出面向对象的优势。
fun main() {
val calculator = CalculatorV2()
calculator.start()
}
除了计算器本身需要面向对象,我们的输入表达式也可以抽象出一个具体模型出来。
我们知道,一个算式分为左边的数字、操作符和右边的数字。因此我们还可以定义一个类,来代表算式表达式。
data class Expression(
val left: String,
val operator: Operation,
val right: String
)
比如,我们想要表达“1 + 2”这个式子的话,我们就可以用这样一个结构来表示:
Expression("1", Operation.ADD, "2")
那么,在完成了面向对象的模型化以后,我们还需要进一步拆分函数的职责与颗粒度。其中,start()方法,主要用于控制程序的流程、输入与输出:
fun start() {
while (true) {
println(HELP)
val input = readLine() ?: continue
val result = calculate(input)
if (result == null) {
println("输入格式不对")
continue
} else {
println("$input = $result")
}
}
}
而calculate()方法,则需要进一步地拆分:
fun calculate(input: String): String? {
if (shouldExit(input)) exitProcess(0)
val exp = parseExpression(input) ?: return null
val left = exp.left
val operator = exp.operator
val right = exp.right
return when (operator) {
Operation.ADD -> addString(left, right)
Operation.MINUS -> minusString(left, right)
Operation.MULTI -> multiString(left, right)
Operation.DIVI -> diviString(left, right)
}
}
fun addString(left: String, right: String): String {
val result = left.toInt() + right.toInt()
return result.toString()
}
fun minusString(left: String, right: String): String {
val result = left.toInt() - right.toInt()
return result.toString()
}
fun multiString(left: String, right: String): String {
val result = left.toInt() * right.toInt()
return result.toString()
}
fun diviString(left: String, right: String): String {
val result = left.toInt() / right.toInt()
return result.toString()
}
fun shouldExit(input: String): Boolean {
return input == EXIT
}
fun parseExpression(input: String): Expression? {
// 待完成
}
fun parseOperator(input: String): Operation? {
// 待完成
}
通过以上代码可以看到,我们拆分calculate()方法主要做了三件事:
- 第一,将“是否退出”的逻辑封装到了shouldExit()方法当中,如果将来这部分逻辑变得更复杂,我们只改动这一个方法即可。
- 第二,将算式的解析,封装到了parseExpression()方法当中,而解析算式的时候也需要解析操作符,这时候我们也需要parseOperator()。
- 第三,将具体的计算逻辑交给了对应的方法。这么做的原因,是可以让我们的程序变得更加灵活。比如,我们在下个版本当中会更改“加法”的计算逻辑,那么我们就只需要改动这一个方法就行了。
同时,以上所有独立抽出来的方法,它们也都将变得可测试,这有利于提升程序的稳定性。
到这里,我们对计算器2.0的第一阶段改造就差不多完成了,我们融入了面向对象的思想,也对calculate()方法进行了更细颗粒度的拆分。下一步,我们要做的就是兼容算式的格式,让它能够解析没有空格的算式。
第二阶段:兼容输入格式
现在,假设我们的输入是“1+2”,数字与字符之间没有空格。那在这种情况下,我们就无法使用空格作为分隔符了。所以要换一种方式,想办法从算式当中,解析出操作符“加减乘除”中的一种,然后再用操作符作为我们的分隔符去找出数字。
其实,因为操作符只有这四种情况,所以我们很容易就能想到一种方案,一个个去尝试:
fun parseOperator(input: String): Operation? {
return when {
input.contains(Operation.ADD.value) -> Operation.ADD
input.contains(Operation.MINUS.value) -> Operation.MINUS
input.contains(Operation.MULTI.value) -> Operation.MULTI
input.contains(Operation.DIVI.value) -> Operation.DIVI
else -> null
}
}
虽然,这段代码运行起来没什么问题,逻辑也非常得清晰,但它看起来很丑陋。而且它还有一个坏处:随着枚举类型的增多,我们的逻辑分支也会增多,手动添加起来也特别麻烦。
因此这种情况,我们就应该充分借助 Kotlin枚举的优势,通过遍历的方式来做:
fun parseOperator(input: String): Operation? {
Operation.values().forEach {
if (input.contains(it.value)) {
return it
}
}
return null
}
可以看到,优化后的代码中,我们不再需要手动地去写when的逻辑分支,也不必自己去枚举Operation的每一种情况,就连代码量也降低了很多,即使将来枚举种类增加了,我们也不必修改这部分代码了。
需要注意,以上的代码中,我们用到了集合遍历的语法“forEach”,你可以将它想象成强化版的for循环,它具体的用法我会在后面“Kotlin集合”那一节中讲解。
现在,对于一个算式“1+2”,我们已经可以成功解析出操作符“+”了,接下来要做的,就是通过“+”来分割字符串,将左右两个数字取出来“1”“2”。这个逻辑就很简单了:
fun parseExpression(input: String): Expression? {
// 解析操作符
val operation = parseOperator(input) ?: return null
// 用操作符分割算式,拿到数字
val list = input.split(operation.value)
if (list.size != 2) return null
return Expression(
// 算式左边
left = list[0].trim(),
operator = operation,
// 算式右边
right = list[1].trim()
)
}
以上代码大致分为三个步骤,我们以“1+2”为例:
- 第一个步骤,调用parseOperator()方法解析操作符“+”;
- 第二个步骤,根据操作符分割算式的数字,分割之后得到的会是“1”“2”组成的列表;
- 第三个步骤,将操作符、数字组合成Expression对象。
这里有一个细节需要注意,我们兼容的输入其实有两种情况,第一种是不包含空格“1+2”,那么我们解析出来的数字会是“1”“2”,这种情况下不会有问题;但还有第二种情况包含空格,对于原本正确的格式,我们更应该支持,比如“1 + 2”,被分隔之后的结果会是“1 ”“2”,这两个数字当中是包含空格符的。
所以,我们使用了list[0].trim(),这里的trim()方法就是用于去掉多余空格的。
让我们实际运行一下看看效果:
至此,我们的计算器2.0版本就完成了。在2.0版本的实操过程中,我们其实是在原有的基础上,融入了面向对象的思想,将计算器功能收拢到了一个类当中,同时也对计算器内部的方法进行了细颗粒度的拆分。
在这个过程中,我们创建了三个类:“Calculator”类,代表整个计算器;“Operation”枚举类,代表加减乘除四种运算操作符;“Expression”数据类,代表我们算式当中的数字和操作符。之后,我们又对计算器的核心功能进行了更细颗粒度的拆分,提高了程序的灵活性,为我们的功能扩展打下了基础。
好了,现在让我们进入3.0版本的开发吧。
计算器3.0
针对3.0这个版本,我们也分为了两个阶段:
- 第一阶段,增加单元测试。单元测试是软件工程当中的一个概念,它指的是对软件当中的最小可执行单元进行测试,以提高软件的稳定性。在Java当中,最小单元一般会认为是类,因此,我们一般会以类为单元,对类当中的方法进行一一测试。
- 第二阶段,支持大数的加法。我们知道Java、Kotlin当中的整型都是有范围限制的,如果我们输入两个特别大的数字进行计算,那么程序是无法正常工作的。因此,我们需要对特别大的数进行兼容。
下面,我们先来搞定单元测试。
第一阶段:单元测试
在Kotlin当中,如果要使用单元测试,我们需要在gradle文件当中,添加Kotlin官方提供的依赖:
testImplementation 'org.jetbrains.kotlin:kotlin-test'
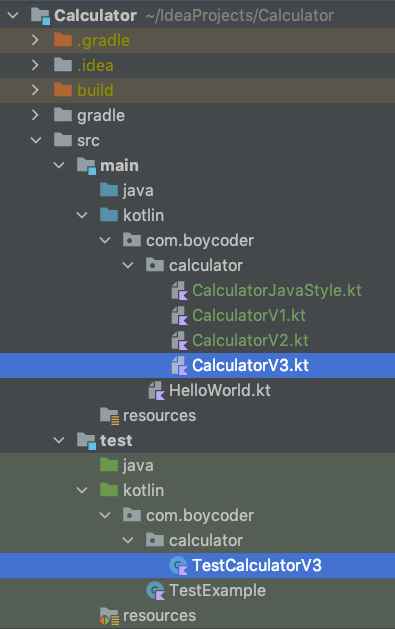
这样,我们的工程就拥有单元测试的能力了。单元测试的代码,我们一般会放在工程的test目录下:
我们可以从这个图中看出很多信息:
- 第一,test目录、main目录,它们是平级的目录,内部拥有着相同的结构。main目录下放的是功能代码,test目录下放的则是测试代码。
- 第二,由于我们要开发3.0版本,所以我们在main目录下创建了CalculatorV3这个类;另外,由于我们需要在3.0版本加入单元测试,所以对应的,我们在test目录下相同的地方,创建了TestCalculatorV3。这两个类的关系是一一对应的,CalculatorV3是为了实现3.0版本的功能,TestCalculatorV3是为了测试3.0版本的功能,确保功能正常。
不过这里你要注意,虽然我们创建了CalculatorV3这个类,但其实它里面的代码还是用的CalculatorV2的代码。3.0版本的功能,我们放到第二阶段才会去实现。
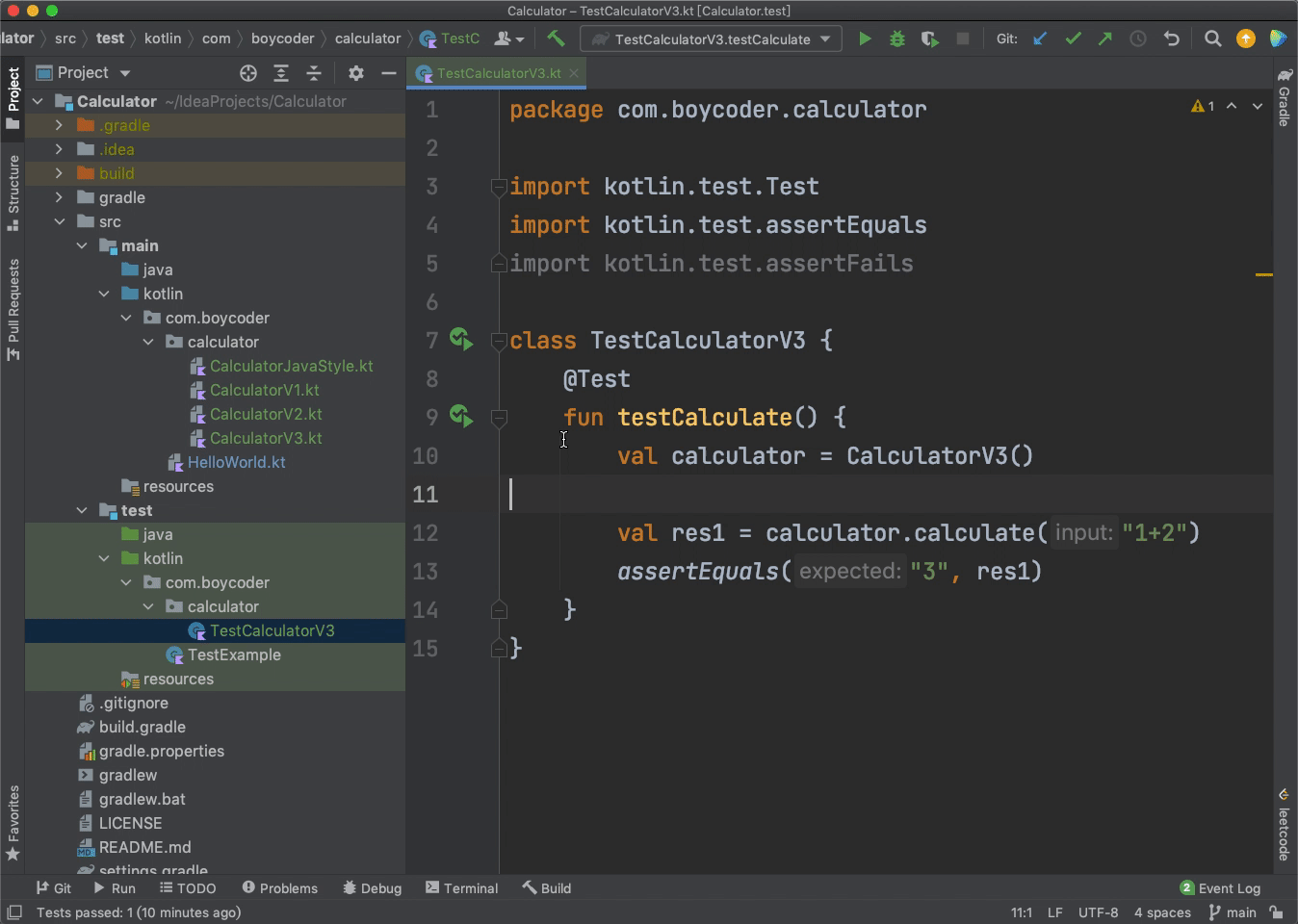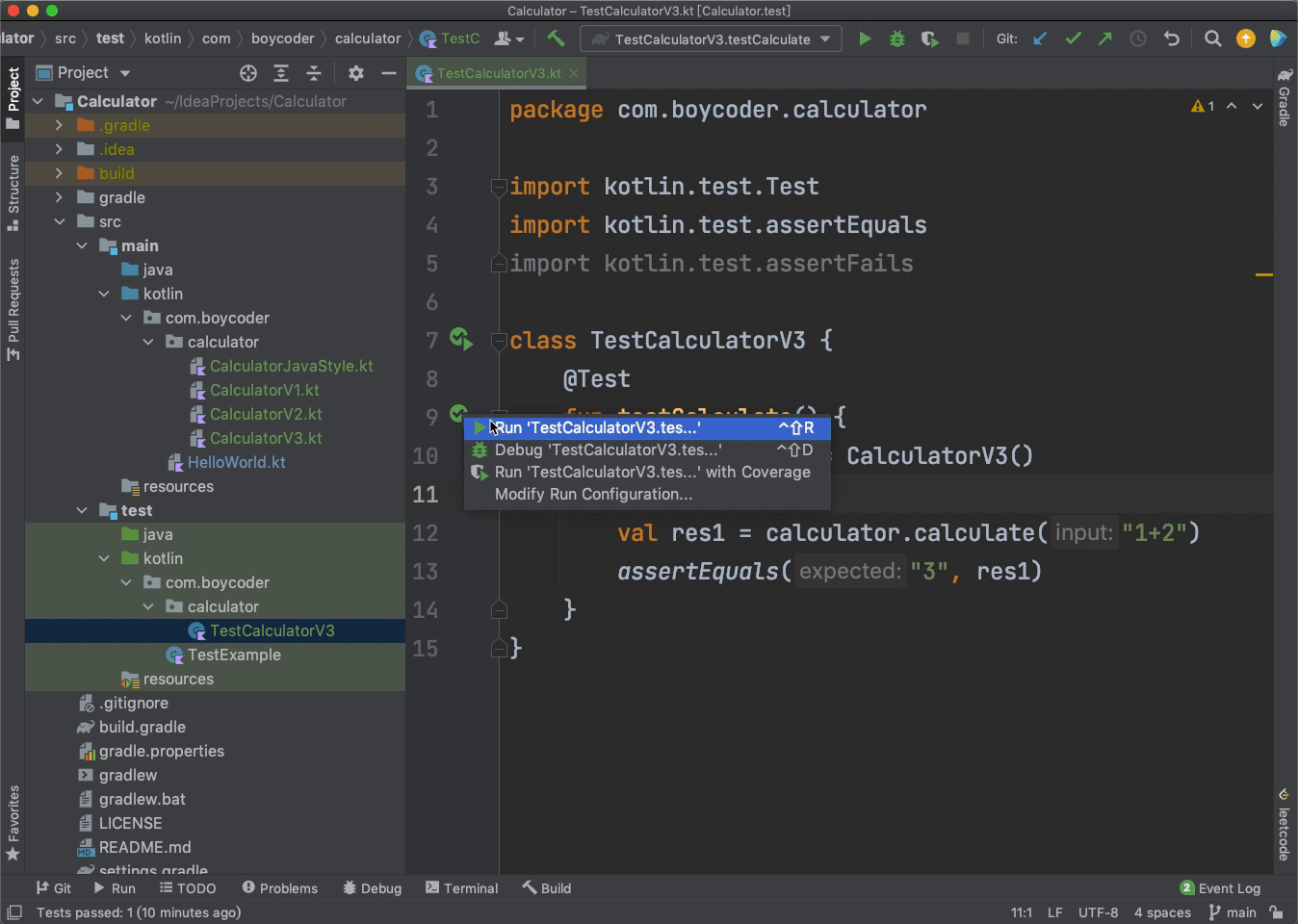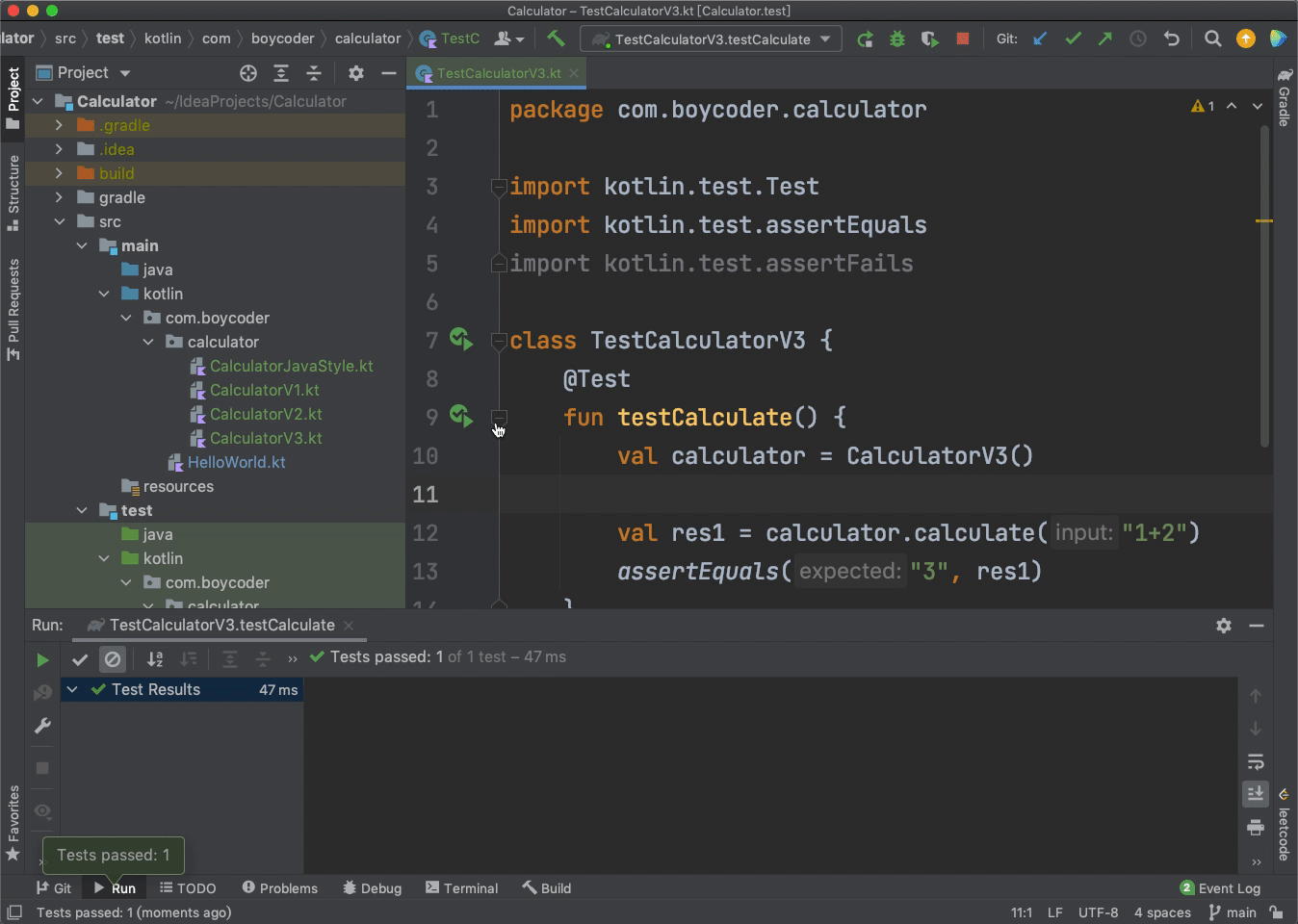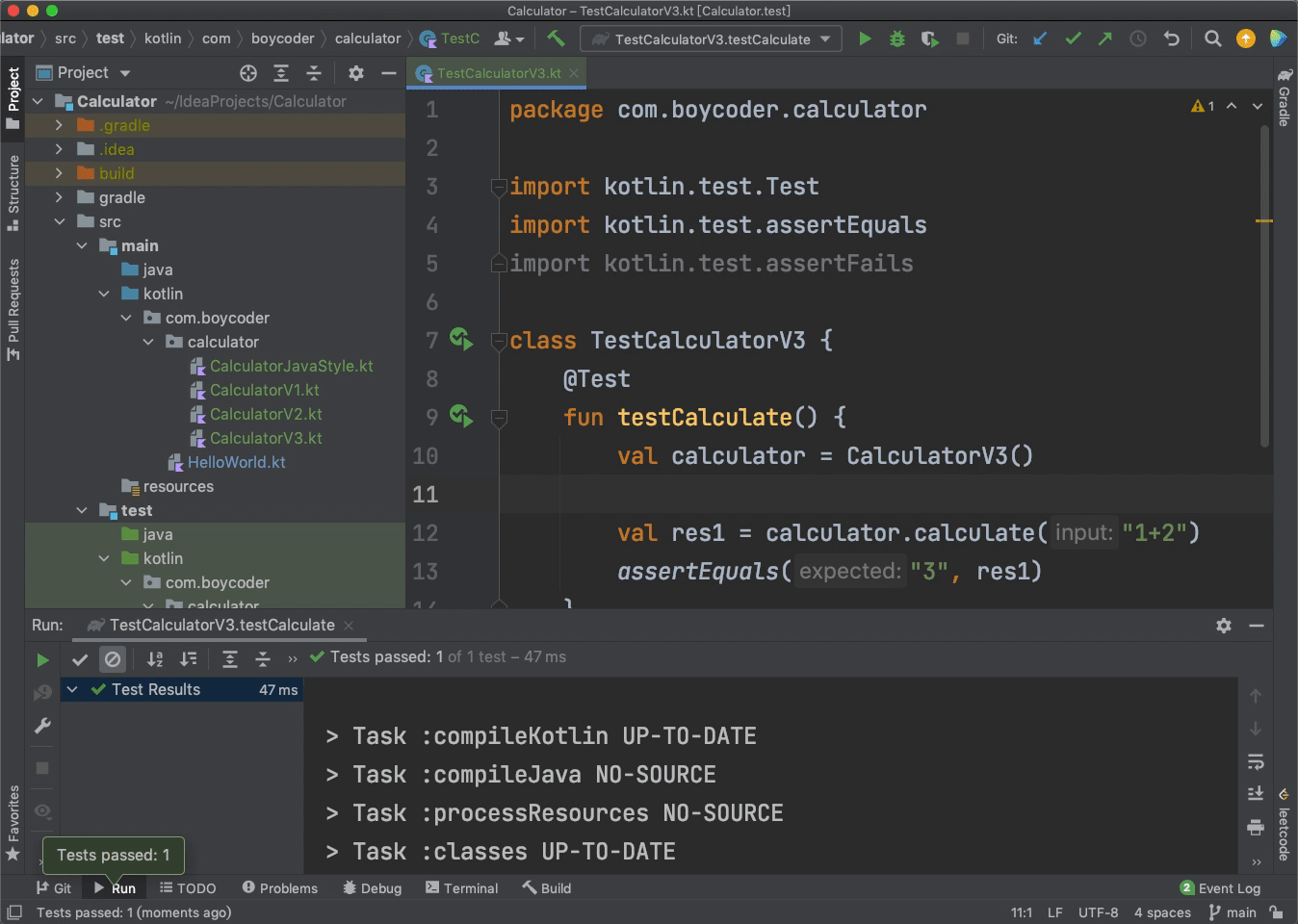
接下来,让我们来编写测试代码:
class TestCalculatorV3 {
@Test
fun testCalculate() {
val calculator = CalculatorV3()
val res1 = calculator.calculate("1+2")
assertEquals("3", res1)
}
}
首先,我们定义了一个方法testCalculate(),并且使用了一个注解@Test来修饰它。因为这样做以后,IntelliJ就会知道:哦,这是一个用来做测试的方法。
接着,我们在testCalculate()当中创建了一个CalculatorV3的对象,然后调用了它的calculate()方法,传入了“1+2”。我们知道,如果程序正常工作的话,返回的结果应该是“3”。因此,我们紧接着就执行了一个断言“assertEquals(“3”, res1)”,它的意思是“res1一定等于3”。如果res1=3,那么我们的单元测试就会成功,否则就会失败。
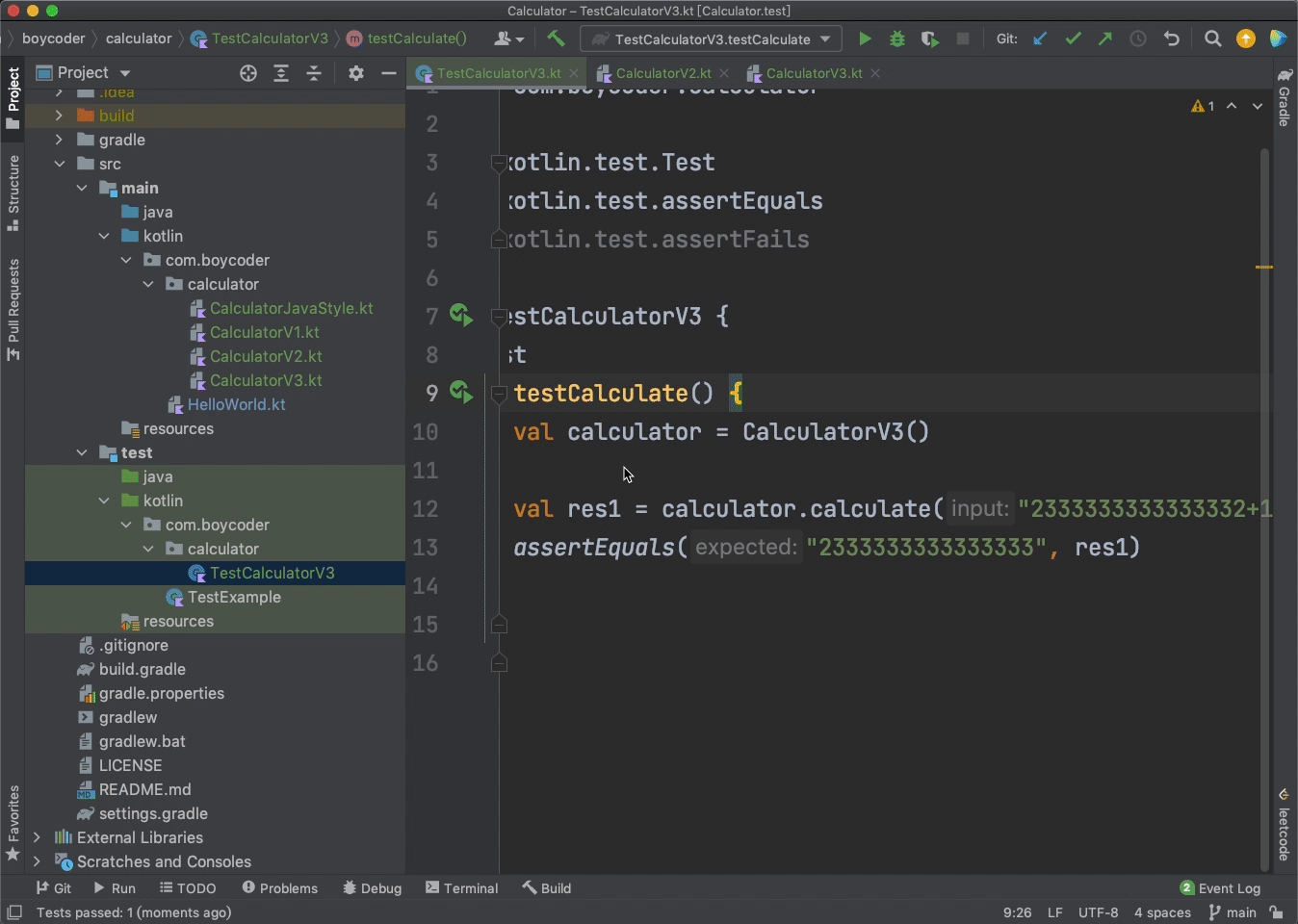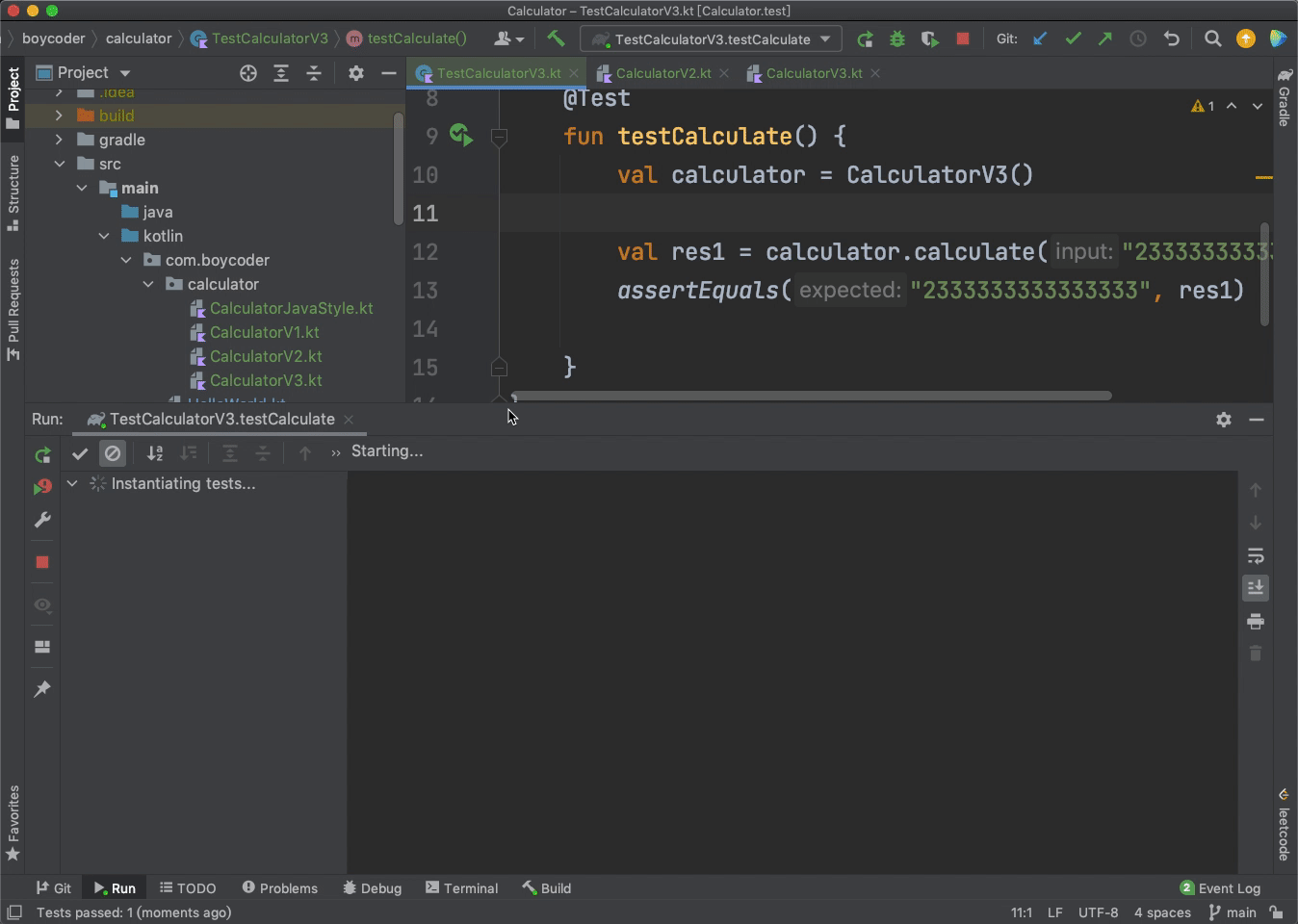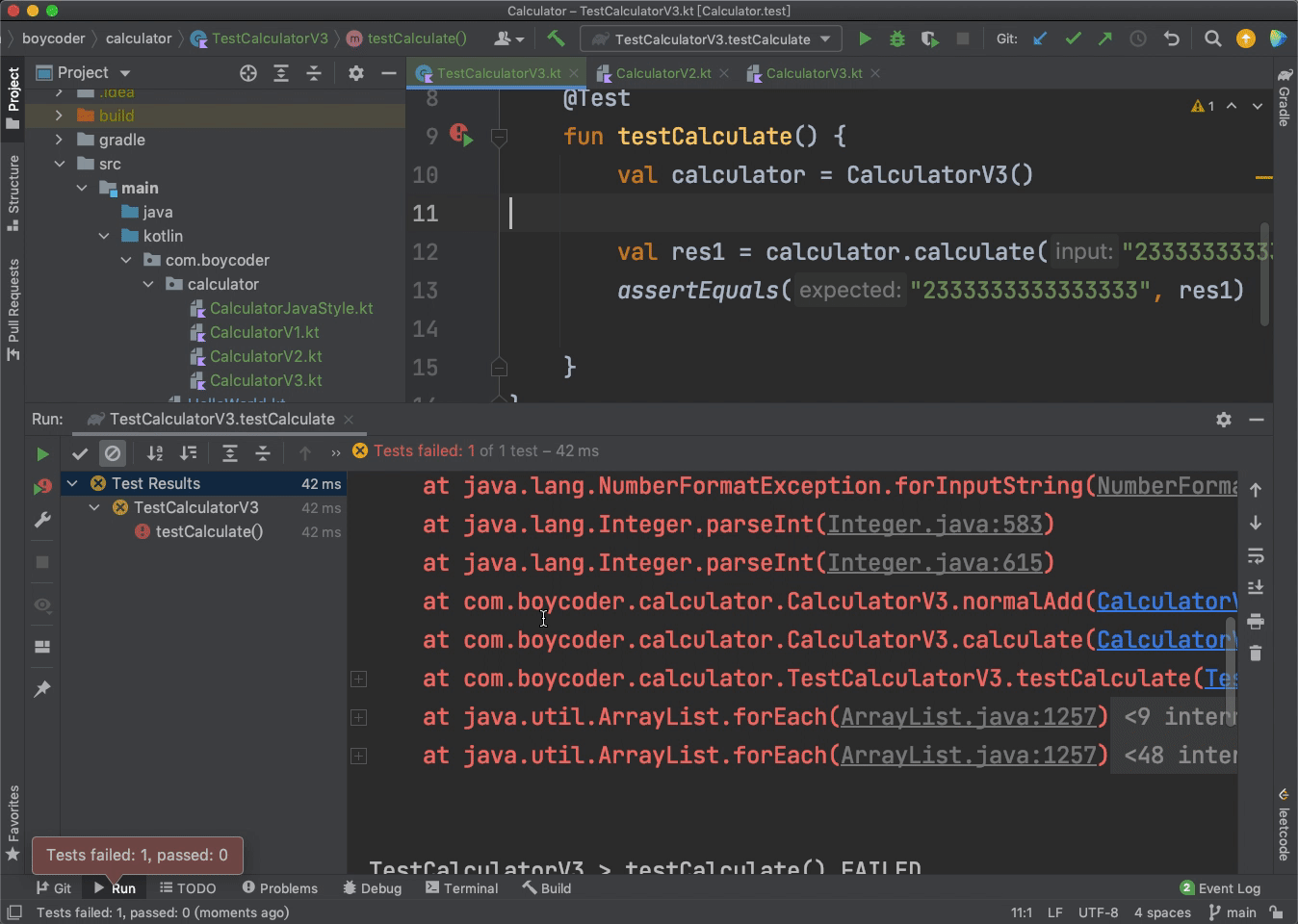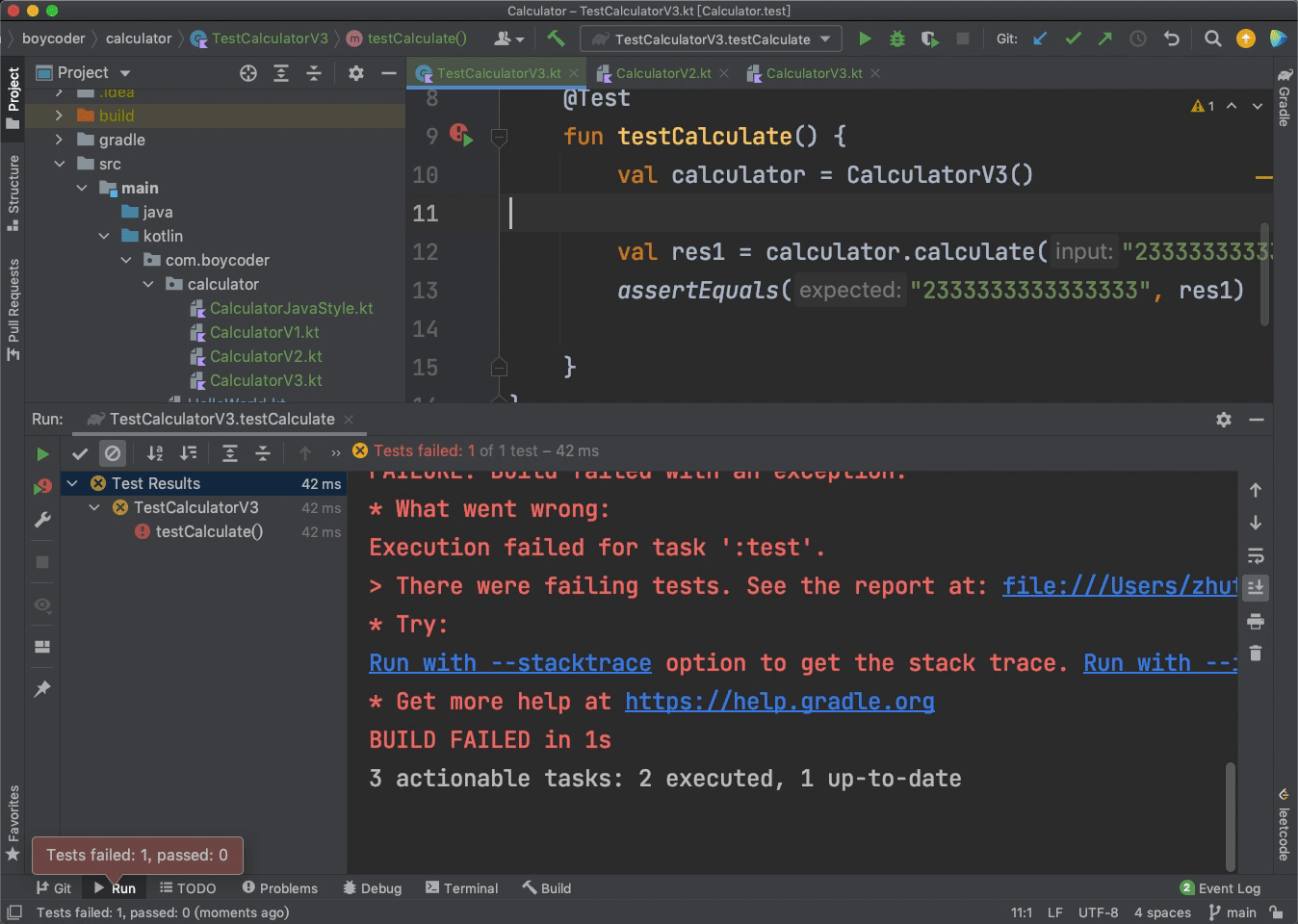
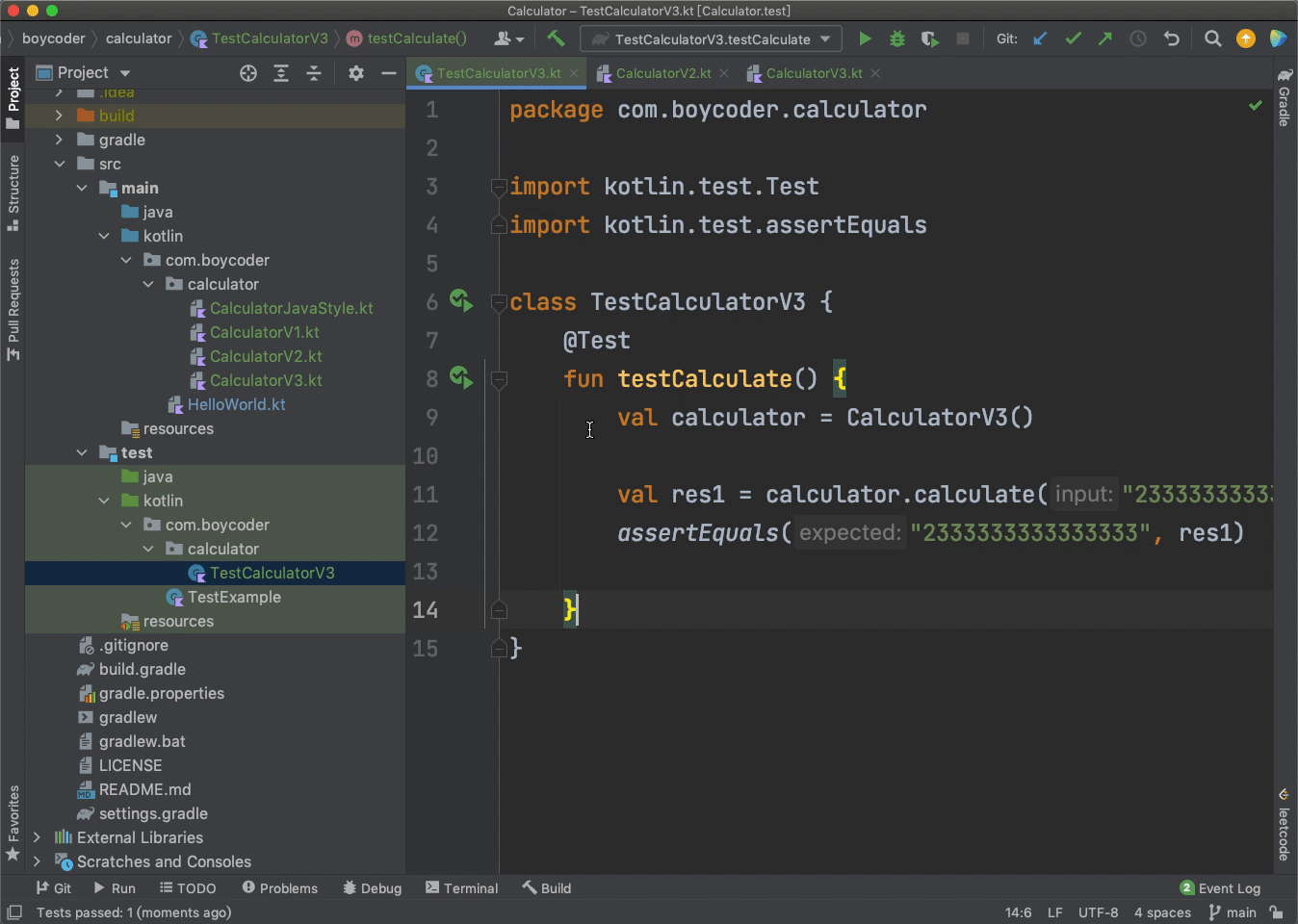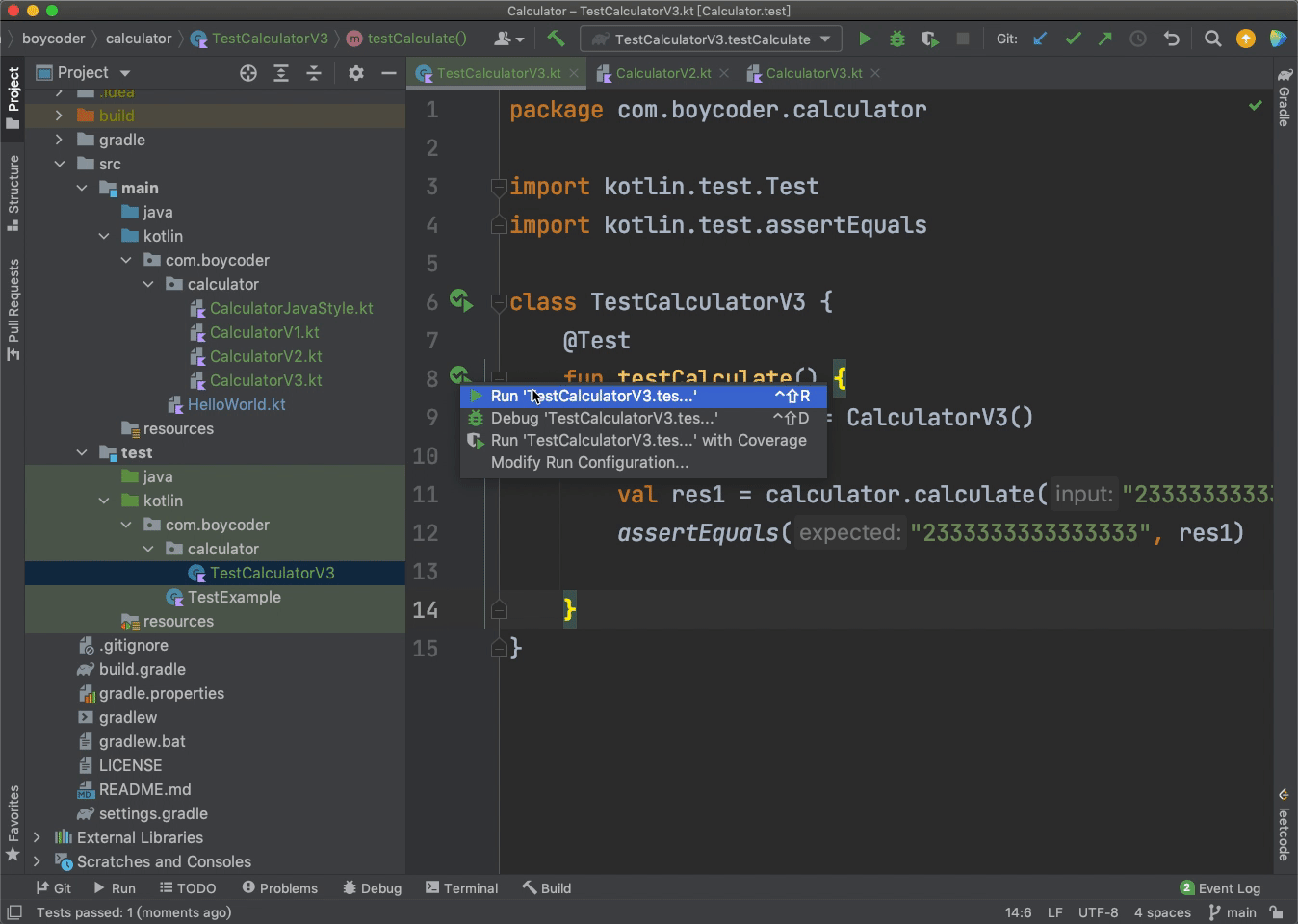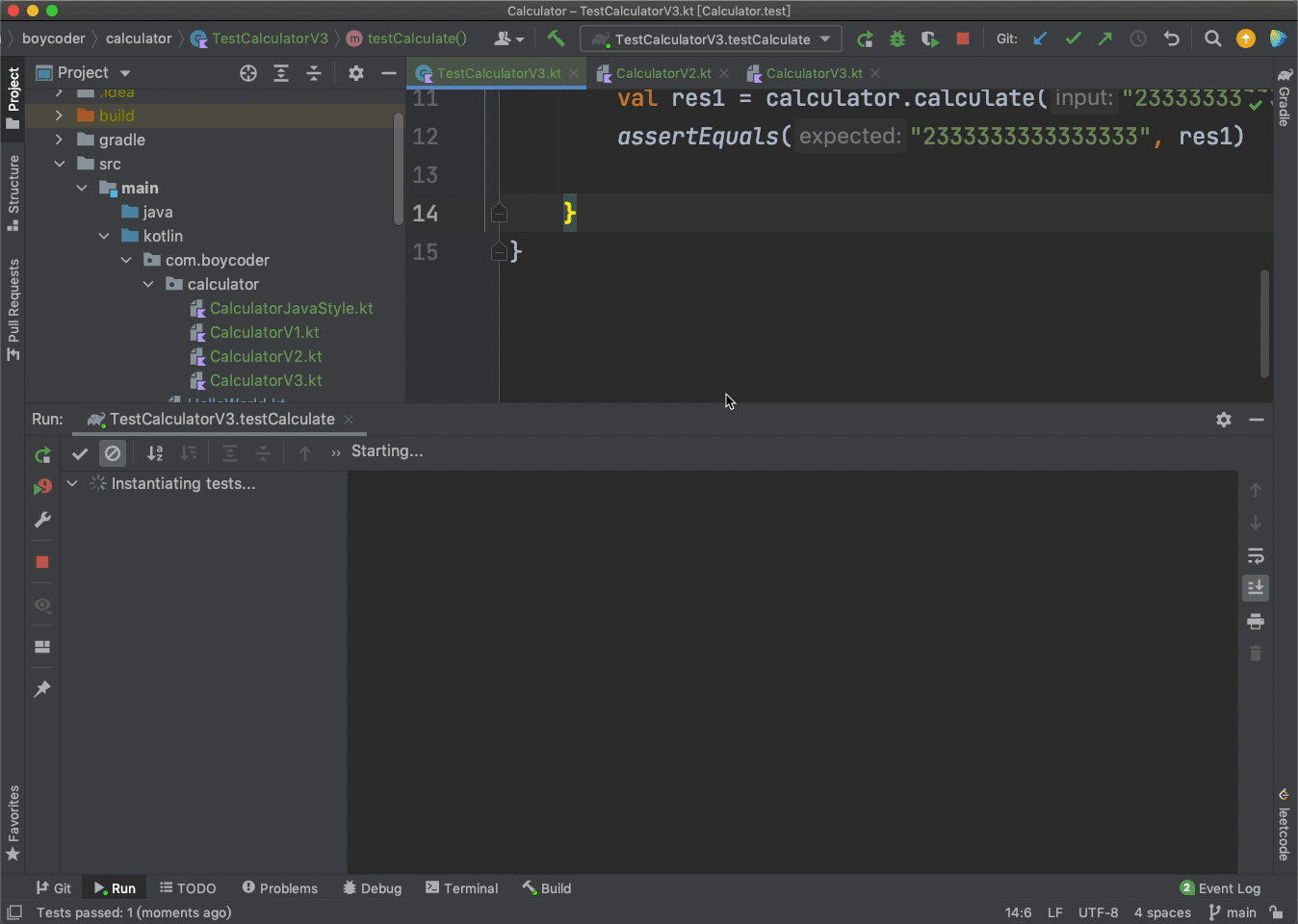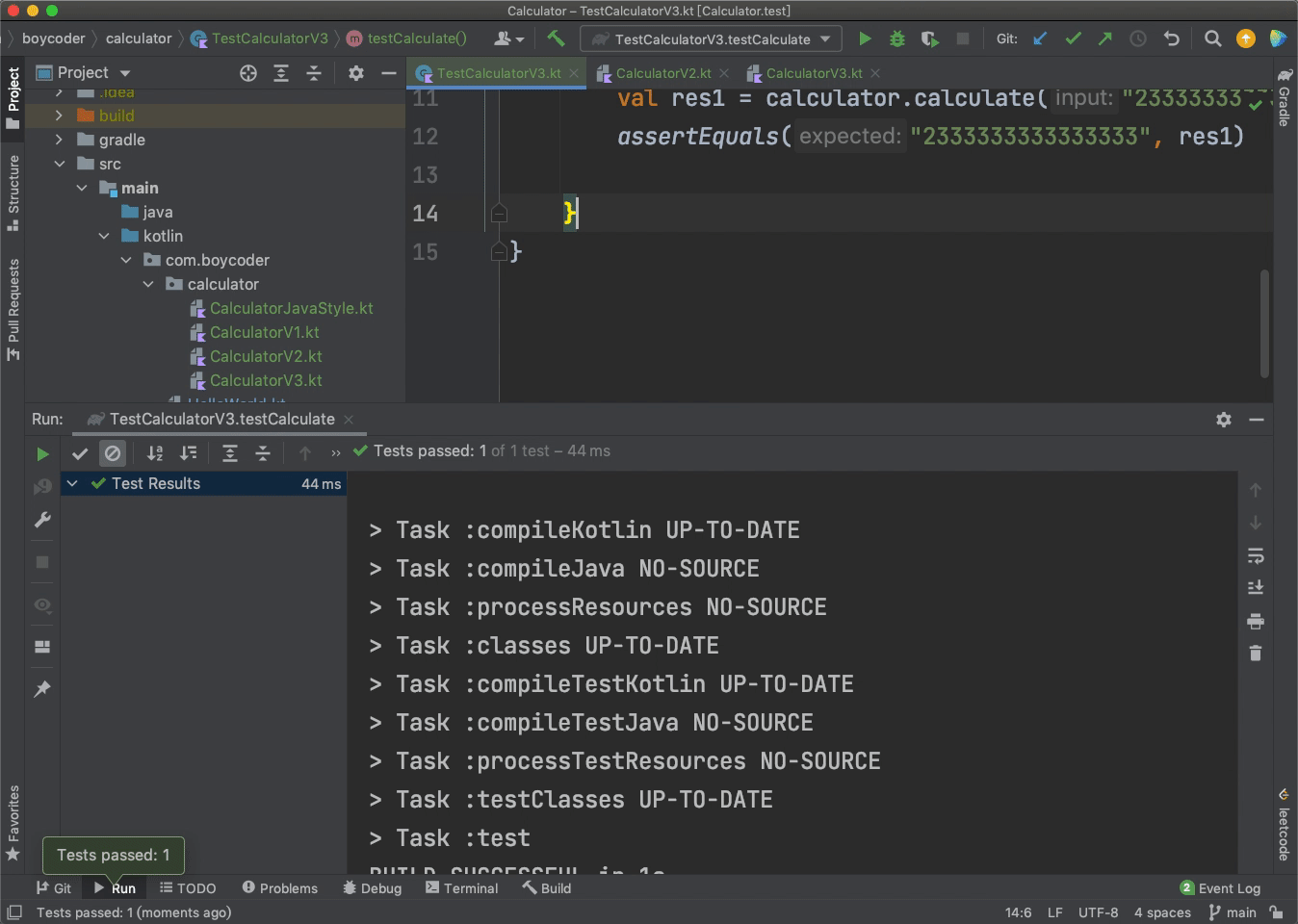
我们可以看看单元测试运行成功的效果:
如果这时候,我们将“1+2”改成大数的加法,比如“2333333333333332+1”,并且将断言也修改一下:
val res1 = calculator.calculate("2333333333333332+1")
assertEquals("2333333333333333", res1)
那么,你觉得单元测试的结果会是怎么样的呢?
单元测试失败了!
具体原因相信你一定也能猜到,因为“2333333333333332”这个数实在太大了,已经远远超出了Int类型的范围,如果不做特殊处理的话,我们的程序是无法正常运行的。而这正好就是我们下一个阶段要做的事情:支持大数的加法。不论多大的两个数字相加,我们都要算出正确的结果。
这个单元测试的代码我们先留着,等我们实现“大数的加法”后,我们再重新运行一遍,这样一来,我们就可以借此验证代码是否正确。
第二阶段:大数加法
大数的加法,其实是我们程序员面试当中的一道高频题。它的解题思路也很简单,就是通过模拟我们手写加法竖式的方法,从个位、十位、百位、千位,一直累加,超过10的时候,我们需要进位。
我们以“135+99”为例:
从上面的手写加法竖式的过程我们可以看出,这个计算其实就是分了三个步骤在进行,分别是个位、十位、百位:
- 个位计算,“5+9=14”,出现进位,这时候我们用carry来存储进位:carry=1,个位结果为4;
- 十位计算,十位相加“3+9=12”,由于之前有过进位,所以应该是“3+9+1=13”,十位结果为3;
- 百位计算,由于99不存在百位,我们自动补零,所以就应该是“1+0+1=2”,百位结果为2。
最终,我们将每一位的结果拼接起来,就得到了最终的结果。有了这样的思路后,我们的代码就很容易实现了。
fun addString(leftNum: String, rightNum: String): String {
// ①
val result = StringBuilder()
// ②
var leftIndex = leftNum.length - 1
var rightIndex = rightNum.length - 1
// ③
var carry = 0
// ④
while (leftIndex >= 0 || rightIndex >= 0) {
// ⑤
val leftVal = if (leftIndex >= 0) leftNum.get(leftIndex).digitToInt() else 0
val rightVal = if (rightIndex >= 0) rightNum.get(rightIndex).digitToInt() else 0
val sum = leftVal + rightVal + carry
// ⑥
carry = sum / 10
result.append(sum % 10)
leftIndex--
rightIndex--
}
// ⑦
if (carry != 0) {
result.append(carry)
}
// ⑧
return result.reverse().toString()
}
上面的代码一共有8处注释,代表了整体的程序流程,让我们一步步来分析:
- 注释①,我们**创建了一个StringBuilder对象,**用于存储最终结果,由于我们的结果是一位位计算出来的,所以每一位结果都是慢慢拼接上去的,在这里,为了提高程序的性能,我们选择使用StringBuilder。
- 注释②,我们定义了两个可变的变量index,它们分别指向了两个数字的个位,这是因为我们的计算是从个位开始的。
- 注释③,carry,我们用它来存储每一位计算结果的进位。
- 注释④,这个 while循环当中,我们会让两个index从低位一直到高位,直到遍历完它们所有的数字位。
- 注释⑤,这里的逻辑是取每一位上的数字,其中有个细节就是补零操作,比如当程序运行到百位的时候,99没有百位,这时候rightVal = 0。
- 注释⑥,当我们的程序计算出结果后,我们要分别算出carry,以及当前位的结果。这时候我们分别使用“除法”计算carry,使用“取余”操作计算当前位的结果。
- 注释⑦,这里是为了兼容一个特殊的场景,在“99+1”的情况下,我们的while循环最多只会遍历到十位,如果不做特殊处理的话,结果将变成“99+1=00”。这并不是我们想要的,所以,为了兼容这种特殊情况,我们在while循环结束后增加了一个判断,如果carry=1,那就说明在最大的那一位数计算完以后,仍然有进位,我们要手动添加。
- 注释⑧,对于一个算式“135+99”,我们的result拼接其实是倒叙的“432”,这时候我们需要将其翻转一下,才能得到正确的结果“135+99=234”。
到这里,我们的大数加法功能,就算实现了。让我们回过头,再去运行一次单元测试,来验证下我们的代码是否正确:
果然,在我们兼容了“大数加法”以后,单元测试就可以成功通过了。至此,我们的计算器3.0版本就算是完成了。
在这个版本的开发过程中,首先我们引入了单元测试,通过这种方式,我们可以测试代码逻辑是否正确,并可以辅助我们排查问题。接着,我们写了一个“2333333333333332+1”的测试用例,并且失败了,不过在完成大数加法的功能后,这个测试也最终通过了。
这里我需要特殊说明的是,为了不偏离本次实战课的目的,我们的单元测试只写了两个,但在实际的开发工作当中,单元测试是需要尽量覆盖所有情况的。换句话说,仅仅只是测试“1+2”“2333333333333332+1”这两种情况,是无法保证我们的计算器逻辑正确的。一般来说,一个应用于商业的计算器,它的单元测试用例数量会达到几百上千个。
小结
到这里,我们就通过完成三个不同版本的四则运算计算器,一起梳理了前面课程中,学习的那些重要的Kotlin的知识点,比如不可变的变量val、when表达式、数据类、枚举类,等等。并且也在实操过程中,一起思考了代码实现时可能会出现的问题。
你也可以在动手操作的过程中,具体感受下跟Java代码的不同,同时也看看自己的思路与课程的思路有什么不同,课程当中的代码还有哪些可以改进的地方。
最后我想让你注意的是,在3.0版本中,我们引入了单元测试功能。实际上,单元测试的作用,不仅仅可以验证新开发的功能,同时它还可以用于保证旧的功能不受影响。在实际开发工作中,我们很容易因为对功能A的改动,导致功能B出问题。然后往往由于时间限制,测试人员只测试了功能A,忽略了功能B,最终导致线上故障带来经济损失。
而借助单元测试,在每一次的开发工作完成以后,我们就统一跑一遍所有的单元测试,只要单元测试通过了,我们就能保证,新的功能没问题,而旧的功能也没问题。
动手实操
在3.0版本的开发当中,我们仅仅只实现了“大数的加法”,其余的“大数的减法”“大数的乘法”“大数的除法”都没有实现。请你挑其中一个功能,尝试自己实现,参考答案我会在之后放出来。
欢迎你在评论区分享你的实现思路,我们下节课再见。