106 lines
12 KiB
Markdown
106 lines
12 KiB
Markdown
# 04 | 随机对照试验:章鱼保罗真的是“预言帝”么?
|
||
|
||
数据给你一双看透本质的眼睛,这里是《数据分析思维课》,我是郭炜。
|
||
|
||
你在生活中是否遇到过这样的现象:你参加了个小型聚会,竟然遇到了同月同日出生的人,你慨叹有缘的时候,可能并不知道这只是一个高概率事件?新做的一个界面UI,用户调查显示客户满意度明显高于老版本,你的领导却跟你说这是“幸存者偏差”?以及,你觉得曾经在南非世界杯上“成功预测”德国小组赛赛果的“预言帝”章鱼保罗,真的有预测能力吗?
|
||
|
||
要真正了解这背后的玄机,就要理解作为数据分析界最伟大的原理之一的“**随机对照试验**”。不过在进入正题之前,你先要弄清楚一个重要的概念——“**随机**”。你可能觉得这个很简单,“随机”不就是要确保每个个体被抽取的概率相同么?但是生活中充斥着太多的“伪随机”,会影响我们的判断结果。那到底什么是伪随机呢?我们接着往下看。
|
||
|
||
## 你认为的随机其实都是“伪随机”
|
||
|
||
我们来玩一个小游戏:你现在闭上眼睛,马上在0到20之间想一个数,然后我来猜。好,想好了吧?我可以告诉你,大概率你不会选5和15这两个数字。不信的话,你不妨试一试,或者和朋友们玩一下这个小游戏。
|
||
|
||
为什么我会这么确信你大概率不会选5和15呢,**因为人脑在选择随机数的时候,会刻意规避一些有规律的数字,这反而让这些随机数变得“不随机”了。**
|
||
|
||
同样,刚刚说的用户反馈的例子就很典型。大部分用户其实并不愿意花时间填写设计的调查问卷,一般愿意填写的都是对这个产品比较感兴趣的人,或者使用度比较高、希望产品能有一些改进的人。因此这样让用户填写反馈,往往会产生“伪随机”这个问题。
|
||
|
||
所谓伪随机,就是看上去产生的过程似乎是随机的,但实际上是确定的。例如计算机的随机数,这是通过确定性的算法计算出来的,让你随意想一个数字,这也是根据你个人习惯偏好想出来的,它们都属于伪随机数。
|
||
|
||
也就是说,如果我们选择样本的随机程度不够,或者我们自己对数据的理解程度不够,就经常会出现一些“小确幸”的事情:我们可能会认为幸运和缘分这样的东西,出现的概率还挺高的。
|
||
|
||
其实不然,就拿开头提到的聚会来说,如果聚会超过50人,那有两个人是同一天生日的概率高达97%,即使是20人的小聚会至少两人生日相同的概率也高达41%,你可以参考下图的计算过程。
|
||
|
||

|
||
|
||
## 随机对照试验帮助你去伪存真
|
||
|
||
了解完“随机”这个概念后,我们就进入到今天的主题——**随机对照试验**。现在无论是医疗行业的临床医学、生物科学的基因遗传学,还是互联网黑客增长理论当中的A/B测试,都运用到了这个理论。它帮我们解决了一个问题,就是**当我们不知道客观世界里一个问题的真正答案的时候,可以通过少量的数据来验证非常大的数据规律**。
|
||
|
||
随机对照试验是由“现代统计学之父”、数据分析的鼻祖——罗纳德·艾尔默·费希尔在《试验设计》一书中提出的,他用了一个很简单的例子来验证一件事情是否真实可信。
|
||
|
||
这就是著名的**奶茶试验**,它很简单地讲述了“随机对照试验”的原理。20世纪20年代,英国有一位女士说道:“先放红茶和先放牛奶的奶茶的味道完全不一样,我一下子就能尝出它们的区别来。”这时刚巧数据分析界的大神费希尔也在场,他就提议通过试验来鉴别这位女士所述的真伪。
|
||
|
||
于是,费希尔设计了一个试验:他在那位女士看不见的地方,为她准备了两种冲泡方法不同的奶茶。之后把奶茶随机摆成一排,共10杯,让女士随机品尝奶茶并说出其冲泡方式,结果那位女士的回答完全准确。这时费希尔得出结论:这位女士真的有某种方法可以分辨出按不同方法冲泡的奶茶。
|
||
|
||
注意这一点,为什么费希尔要用**随机排列**的方式来做这个试验呢?你想想看,假设只是给女士一杯先放红茶的奶茶,即使她判断正确也不能证明她有准确的分辨能力,因为这位女士有50%的概率是可以猜中的,不能排除运气的成分。
|
||
|
||
那么将两种奶茶交替给那位女士,如果她每次都能说中,这能证明她的分辨能力吗?我的答案还是否定的。因为只要有某种规律存在,她只需猜中第一杯奶茶的结果,自然也就能知晓后面的结果了。同理,类似连续给五杯先放红茶的奶茶,然后再连续给五杯先放牛奶的奶茶这样的方法也是不行的。
|
||
|
||
因此**只有在随机的情况下**这个公式才能成立:
|
||
|
||
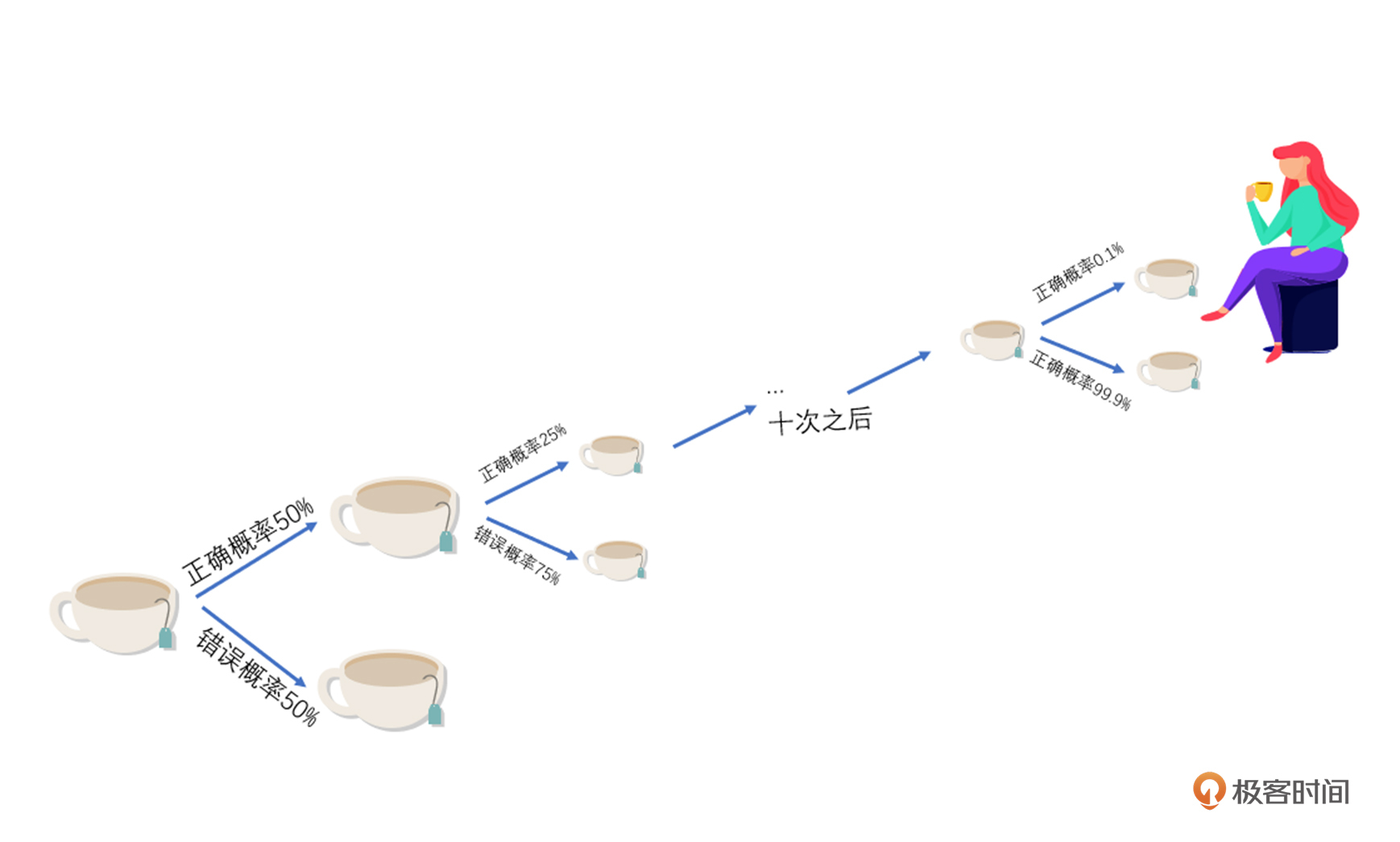
* 如果给女士一杯奶茶,偶然猜对的概率是1/2,也就是50%;
|
||
* 如果随机给女士五杯奶茶,那么她都偶然猜对的概率就是1/2的5次方,大概3.1%;
|
||
* 如果这位女士随机品尝了十杯奶茶,那么偶然猜对的概率,也就是2的10次方分之一,也就是约0.1%。
|
||
|
||
|
||
|
||
试验结果是这位女士将随机选的十杯奶茶都说对了,如果她没有分辨方法,纯粹靠猜的话只有1‰的猜对概率,这是很难实现的。所以,费希尔认为这位女士的确有某种方法可以分辨奶茶的冲泡方法。
|
||
|
||
“奶茶试验”就是随机对照试验的鼻祖,正式的随机对照试验会把研究对象进行随机化分组,并设置对照组。随机分组遵从双盲设计的前提条件,也就是研究者和受试者双方均无法知晓分组结果,最终通过结果来证明到底测试试验是否真的有效。
|
||
|
||
你要记住,这种试验的重点有两个:一是“**随机**”,二是**对照试验**。
|
||
|
||
## 幸存者偏差并不是随机对照试验
|
||
|
||
这时候你可能就开始晕了,我们开头提到的章鱼保罗的预测不就是随机对照试验吗?如果随机的十组比赛它全部都猜对了,那保罗是不是就是真有预言能力呢?
|
||
|
||
并不是这样的。接下来我要给你介绍一个特别容易和随机对照试验混淆的概念,它叫**幸存者偏差**。
|
||
|
||
**幸存者偏差就是**当取得资讯的渠道仅来自幸存者时,我们得出的结论可能会与实际情况存在偏差。因为这样做看上去结果的确是由随机对照试验产生,但在逻辑上是错误的,这其实是在用结果来倒推整个前期数据的产生过程。
|
||
|
||
幸存者偏差这个概念来源于二战时期,那时候有各种地面防空作战和空战,在密集的炮火下,战机机身上几乎所有地方都可能中弹,因此需要用统计学研究战机被击中的部位,从而确定哪个部分需要额外加强装甲。
|
||
|
||
人们对返航的战机进行弹痕分析后发现,飞机机翼和尾部被打穿的弹孔较多,由此得出应该是加强机翼的装甲防护会更好。
|
||
|
||
但对返航的飞机样本来说,其实是说明即使机翼中弹,飞机也有很大的几率能够返航。对于那些弹孔不多的部位来说(比如驾驶舱、油箱和机尾),当这些部位中弹的时候,飞机很可能连飞回来的机会都没有了,而这并没有统计出来,这就是所谓的“看不见的弹痕最为致命”。最后事实也证明,加强弹孔较少部位的装甲防护是正确的。
|
||
|
||

|
||
|
||
我们再回到“预言帝”章鱼保罗的身上,它其实并非如我们想象一般拥有如此神奇的预测能力。
|
||
|
||
你要知道:只要样本量足够大,就一定会出现一个“幸运儿”,能够“碰巧地”预测对所有的场景。世界杯的预测也是如此,这样大规模的赛事,会有很多人、很多生物参与赛果预测,如此大的样本量自然就诞生了本次预测的“幸运儿”,只是它的名字碰巧叫章鱼保罗罢了。没有章鱼保罗,我们还会有另一个“幸运儿”猫咪汤姆(这当然只是我杜撰的名字)。
|
||
|
||

|
||
|
||
在章鱼保罗之外,其实有很多的预测者“牺牲”在了随机概率里,它们不够“幸运”不能被我们看见,只有章鱼保罗足够幸运,成为了能够被我们看到的“幸存者”。另外,从章鱼保罗自身的预测结果来看,你会发现其实我们只是看到了它预测成功的部分,忽略了它也有预测不成功的时候,这也是另一种幸存者偏差。
|
||
|
||
还记得前面我们在讲大数定律试验时的一个现象吗?我们找全世界的人来玩抛硬币游戏,每人抛10次,总会有人连续10次都是正面,然后我们就可能称他为“赌神”,误以为他可以控制抛硬币的结果,这和章鱼保罗是一样的道理。
|
||
|
||
其实,**并没有“预言帝”和“赌神”的存在,我们看到的只是大规模数据背后的“幸存者”。**
|
||
|
||
所以我们要验证章鱼保罗能力的话,我们应该从一开始就把它安置在一个没有任何信号干扰的环境里让它连续预测十次,这样它的成功概率是1%,我们还可以提高预测次数来检测它是不是真的有那么神奇的预测能力。
|
||
|
||
所以当你再看到类似“读书无用论”、“工作都是别人的好”之类的说法时,请你留个心眼,想想我们这节课讲的知识,这些说法到底是不是一种幸存者偏差?
|
||
|
||
以及当你看到一些“成功学大师”向你兜售一些成功心法时,不要盲从所谓的权威,如果有可能,我们最好站得高一些,从多个经济周期的维度去评判某件事物或者某个人。
|
||
|
||
最后,不要总想着如何从成功者那里学习如何成功,也要从失败的人那里总结为什么会失败,因为成功很大程度上来说,就是一个去避免失败的过程。毕竟别人的成功你不一定能复制,但别人踩的坑,你若不注意,很大几率你也会摔一跤。
|
||
|
||
## 总结
|
||
|
||
回顾一下今天所讲的内容,我给你讲了**随机**和**随机试验**,也介绍了一下**幸存者偏差**。
|
||
|
||
现在,随机对照试验被广泛用于临床医学、遗传学以及我们日常的A/B测试当中,来验证一个理论和假设是否真实,这其实是一个很伟大的进步。但你知道吗?连我们都很熟悉的植物学家孟德尔的遗传学理论的实验都存在着问题(尽管他的理论是正确的)——因为他只选取了对他有利的豌豆样本支撑他论文的观点,而不是采用随机对照试验。
|
||
|
||
**在我们工作和生活当中,一定要注意不能犯同样的“错误”——采用非随机的结果来证明我们的观点,更不能用幸存者偏差——拿结果倒推原因来解释我们的一些结论。**
|
||
|
||
**注意自己“不犯错”是一方面,另一方面我们也要学会“发现错误”,学习前人失败的经验教训。**当你在工作生活里别人和你兜售一些貌似合理论调时,希望你对“沉默的数据”留一个心眼,在看向那些闪闪发光的成功数据时,也要意识到有很多“话少”甚至“不说话”的数据存在。
|
||
|
||
也正因为有这么多“沉默”的数据,我们很难在现实世界得到完整的数据结果。因此我的愿景不是照本宣科地教会你各种各样的数据知识和理论,而是希望能让你对这些数据的分析方法和缘起有更好的理解,最终帮助你在生活中做出更有效的决策。
|
||
|
||
数据给你一双看透本质的双眼,让我们不断精进,去伪存真。
|
||
|
||
## 思考题
|
||
|
||
最后,我们来做个思考题吧。你在工作和学习当中遇到过哪些幸存者偏差的事情呢?后面你是怎么辨认出来这是幸存者偏差的?欢迎你在留言区分享关于幸存者偏差的想法,我们共同探讨!
|
||
|