113 lines
7.2 KiB
Markdown
113 lines
7.2 KiB
Markdown
# 22 | 实用的加权采样算法
|
||
|
||
今天来讲一个非常轻松的话题,这个话题看似和推荐系统没什么关系,但肯定有用,只是在别的推荐系统相关话题里都没人会提。
|
||
|
||
## 一些场景
|
||
|
||
还记得前面讲到的用户画像吗?想象一个场景:你经过辛辛苦苦抓数据,清洗数据,收集用户行为,目的就是给用户计算兴趣标签。
|
||
|
||
这时候你可能会遇到一个两难的问题:如果给用户计算出兴趣标签的权重了,那应该保留多少标签呢?
|
||
|
||
保留太多的话,每次召回候选集时,计算复杂度可不低,只保留少部分吧,那真是手心手背都是肉,生怕丢弃的标签才是用户的真爱。
|
||
|
||
怎么办?这时候,你需要的一个简单的加权采样算法,每次召回时并不使用全部用户标签,而是按照权重采样一部分标签来使用,这样做的好处当然很明显:
|
||
|
||
1. 大大减少召回时的计算复杂度;
|
||
2. 可以保留更多的用户标签;
|
||
3. 每次召回计算时还能有所变化;
|
||
4. 虽然有变化,但是依然受标签的权重相对大小约束。
|
||
|
||
加权采样的应用不只这一个地方,比如在热门排行榜展示时,也可以用加权采样,而不仅仅按照排行榜分数顺序展示,采用加权采样的展示方法,会让排行榜每次刷新都略有变化,人民群众也会更加喜闻乐见。
|
||
|
||
下面介绍几种常用的加权采样算法及其原理,供你日常随手拿来使用。
|
||
|
||
## 加权采样
|
||
|
||
加权采样有两种情况,一种是能够已知全部样本的个数。这需要遍历整个样本,比如说用户标签采样输出,那么每次采样时仍然需要遍历所有的标签,来依次决定每一个标签输出的概率。
|
||
|
||
另一种是不知道总量样本是多大,或者总量很大,以至于你不愿意全部遍历之后再输出采样结果,这样的数据就是数据流,对应的就是流采样。
|
||
|
||
下面分别讲这两种采样方法。
|
||
|
||
### 1.有限数据集
|
||
|
||
等概率采样的方法非常简单,任意编程语言中都有伪随机数实现,就不在本文讨论范围内了。
|
||
|
||
现在假设你有用户标签若干,每一个标签都有个权重w,权重高低反映了用户对这个标签的感兴趣程度高低。你希望每次输出一部分标签用于召回推荐候选集,每次输出时都不一样,但是又能反映用户标签的权重,输出的概率和权重成正比。
|
||
|
||
这时候你需要一个公式:
|
||
|
||
$$S\_{i} = R^{\\frac{1}{w\_{i}}}$$
|
||
|
||
解释一下这个公式:
|
||
|
||
1. wi 是每个样本的权重,比如用户标签权重;
|
||
2. R是遍历每个样本时产生的0到1之间的随机数;
|
||
3. Si就是每个样本的采样分数
|
||
|
||
遍历之后,按照采样分数排序,输出前k个结果就是你得到的采样结果。可以编程简单做个模拟,比如下面有这样几个简单样本。
|
||
|
||
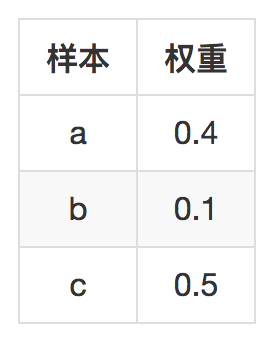
|
||
|
||
模拟10000次后,三个样本被采样次数如下:
|
||
|
||
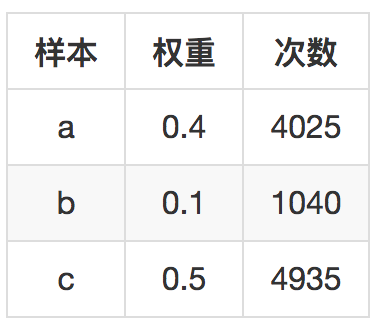
|
||
|
||
你可以看到,每个样本采样概率和它的权重成正比。
|
||
|
||
还有另一种加权采样方法,是利用指数分布。
|
||
|
||
我先给忘记了指数分布的人复习一下什么是指数分布。
|
||
|
||
假设你到银行去办业务,每个人办理业务的时间是不确定的,那每个人办理业务时间的概率分布就是指数分布,用教科书上的话说,就是两个事件发生的时间间隔。
|
||
|
||
指数分布的概率密度函数是:
|
||
|
||
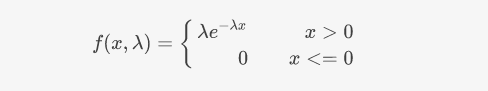
|
||
|
||
指数分布的参数Lambda,它的倒数,$\\frac{1}{\\lambda}$ 就是事件发生时间间隔的期望。把指数分布的这个意义放进标签中来考虑,标签的权重其实反映一个直觉:权重越大的标签,用户消费它就越频繁,也就是间隔时间就会短。
|
||
|
||
所以根据这个原理,就有另一个加权采样的办法:为每一个标签构造一个指数分布随机数,这个指数分布的参数Lambda就是标签权重,然后用这个指数分布的产生一个随机数,再输出随机数最大的k个标签作为采样结果,是不是很完美?
|
||
|
||
还是上面的权重,再来模拟10000次。
|
||
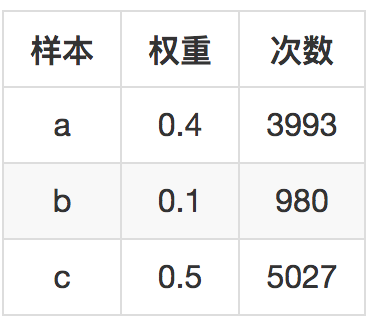
|
||
|
||
依然完美符合权重的相对大小。
|
||
|
||
### 2.无限数据集
|
||
|
||
上面的两种采样都是针对有限数据集的,也就是采样之前都要遍历一遍所有样本。那么如果面对的数据集无限大,或者不知道多大时,该怎么做加权采样呢?这就要讲到另一个采样算法了,名字叫蓄水池采样(也叫蓄水池抽样)。
|
||
|
||
蓄水池采样可以用在推荐系统的哪些地方呢?比如可以再模型融合之后加一层蓄水池抽样,或者在召回阶段加一层蓄水池采样,这样在不影响整个推荐流程和转化概率的前提下,降低计算复杂度和提升推荐多样性。
|
||
|
||
或者,在线阶段要使用用户的反馈行为做实时推荐,对于不同的用户,活跃程度不同,产生的反馈行为数量不同,你也可以用蓄水池采样,为每个用户取出固定数量的行为用于更新推荐结果。
|
||
|
||
下面,我先讲蓄水池采样,再讲加权蓄水池采样。
|
||
|
||
假如有一个数据集合,一共有n条,要从中采样取出k个,那么每个样本被选中的概率就是 $\\frac{k}{n}$ 。蓄水池采样的做法是:
|
||
|
||
1. 直接先取出前k个样本留着,这k个就是随时准备最终要输出的;
|
||
2. 从第k+1个开始,每个都以 $\\frac{k}{n}$ 的概率去替换那留着的k个样本中的一个。
|
||
|
||
这个过程,随时可以取用那个k个集合作为输出结果,任意时刻,当总样本遍历了n个时,他们的概率都是 $\\frac{k}{n}$ 。这就是蓄水池采样,蓄水池采样,顾名思义,k个元素的样本集合就是个蓄水池,是任意时刻的采样结果,可以随时取用。
|
||
|
||
现在回到我们今天的主题来,实际上更需要的是加权蓄水池采样。加权蓄水池采样利用的依然是在前面说的第一种加权采样方法,只不过结合了蓄水池采样的思想。
|
||
|
||
要从大数据集中采样k个,其具体做法是这样的:
|
||
|
||
1. 为每一个样本生成一个分数,分数还是用这个公式 $S\_{i} = R^{\\frac{1}{w\_{i}}}$;
|
||
2. 如果结果不足k个,直接保存到结果中;
|
||
3. 如果结果中已经有k个了,如果 $S\_{i}$ 比已有的结果里最小那个分数大,就替换它。
|
||
|
||
## 总结
|
||
|
||
今天介绍的算法非常简单,但是在推荐系统中有很多的用途。尤其是面对的数据需要采样、需要有所变化时,加权采样本质上来说就是让权重影响采样概率。
|
||
|
||
前面的几种加权采样算法,都是让采样概率和权重成正比,这意味着你的样本权重之间的关系要合理。
|
||
|
||
那么,请思考另一个问题,如果你的样本权重有正有负,该如何加权采样呢?欢迎留言一起讨论。
|
||
|
||
感谢你的收听,我们下次再见。
|
||
|
||

|
||
|