304 lines
16 KiB
Markdown
304 lines
16 KiB
Markdown
# 39|中端优化第2关:全局优化要怎么搞?
|
||
|
||
你好,我是宫文学。
|
||
|
||
上一节课,我们用了一些例子,讨论了如何用基于图的IR来实现一些优化,包括公共子表达式删除、拷贝传播和死代码删除。但这些例子,都属于本地优化的场景。也就是说,在未来生成的汇编代码中,这些代码其实都位于同一个基本块。
|
||
|
||
不过,复杂一点的程序,都会有if语句和循环语句这种流程控制语句,所以程序就会存在多个基本块。那么就会存在跨越多个基本块的优化工作,也就是全局优化。
|
||
|
||
所以,今天这节课,我们就来讨论一下如何基于当前的IR做全局优化。同时,为了达到优化效果,我们这一节课还需要把浮动的数据节点划分到具体的基本块中去,实现指令的调度。
|
||
|
||
但在讨论全局优化的场景之前,我还要先给你补充一块知识点,就是变量的版本和控制流的关系,让你能更好地理解全局优化。
|
||
|
||
## 变量的版本和控制流的关系
|
||
|
||
通过前几节课我们已经知道,我们的IR生成算法能够对一个变量产生多个版本的定义,从而让IR符合SSA格式。可是,我们是如何来表示不同版本的定义的,又是如何确定程序中到底引用的是变量的哪个版本呢?
|
||
|
||
在IR的模型中,我引入了一个VarProxy类,来引用变量的一个版本,就像d0、d1和d2,也有的文献把变量的一个定义叫做变量的一个定值。VarProxy里面保存了一个VarSymbol,还包括了一个下标:
|
||
|
||
```plain
|
||
//代表了变量的一次定义。每次变量重新定义,都会生成一个新的Proxy,以便让IR符合SSA格式
|
||
class VarProxy{
|
||
varSym:VarSymbol;
|
||
index:number; //变量的第几个定义
|
||
constructor(varSym:VarSymbol, index:number){
|
||
this.varSym = varSym;
|
||
this.index = index;
|
||
}
|
||
get label():string{
|
||
return this.varSym.name+this.index;
|
||
}
|
||
}
|
||
|
||
```
|
||
|
||
每次遇到变量声明、变量赋值,以及像i++这样能够导致变量值改变的语句时,我们就会产生一个新的变量定义,也就是一个VarProxy。这个VarProxy会被绑定到一个具体的DataNode上。所以,我在IR中显示DataNode节点的时候,也会把绑定在这个节点上的变量定义一并显示出来。
|
||
|
||
那当我们在程序中遇到一个变量的时候,如何确定它采用的是哪个版本呢?
|
||
|
||
这就需要我们在生成IR的过程中,把VarProxy与当前的控制流绑定。每个控制流针对每个变量,只有一个确定的版本。
|
||
|
||
```plain
|
||
//把每个变量绑定到控制流,从而知道当前代码用到的是变量的哪个定义
|
||
//在同一个控制流里,如果有多个定义,则后面的定义会替换掉前面的。
|
||
varProxyMap:Map<AbstractBeginNode,Map<VarSymbol,VarProxy>> = new Map();
|
||
|
||
```
|
||
|
||
在这里,我们还用了一个AbstractBeginNode节点来标识一个控制流。因为每个控制流都是存在一个起点的。而每个控制流节点,透过它的predecessor链,总能找到自己这条控制流的开始节点。
|
||
|
||
```plain
|
||
//获取这条控制流的开头节点
|
||
get beginNode():AbstractBeginNode{
|
||
if (this instanceof AbstractBeginNode){
|
||
return this;
|
||
}
|
||
else{
|
||
return (this.predecessor as UniSuccessorNode).beginNode;
|
||
}
|
||
}
|
||
|
||
```
|
||
|
||
但是,如果变量不是在当前控制流中定义的,而是在前面的控制流中定义的,那我们可以递归地往前查找。这里具体的实现,你可以参考一下[getVarProxyFromFlow()](https://gitee.com/richard-gong/craft-a-language/blob/master/39-40/ir.ts#L701)。
|
||
|
||
最后,如果控制流的起点是一个merge节点,那这个变量就可能是在分支语句中定义的,那我们就要生成一个Phi节点,并把这个Phi节点也看成是变量定义的一个版本,方便我们在后续程序中引用。
|
||
|
||
好了,相信现在你已经可以更清晰地理解变量版本与控制流之间的关系了。现在我们基于这些前置知识,就可以开始讨论全局优化的场景了。
|
||
|
||
## 全局的死代码删除
|
||
|
||
上一节课,我们实现了基本块中的死代码删除功能。那个时候,我们基本上只需要考虑数据流的特点,把uses属性为空的节点删除掉就行了。因为这些节点对应的变量定义没有被引用,所以它们就是死代码。
|
||
|
||
那么,现在考虑带有程序分支的情况,会怎么样呢?
|
||
|
||
我们还是通过一个例子来分析一下。你可以先停下来两分钟,用肉眼看一下,看看哪些代码可以删除:
|
||
|
||
```plain
|
||
function deadCode2(b:number,c:number){
|
||
let a:number = b+c;
|
||
let d:number;
|
||
let y:number;
|
||
if (b > 0){
|
||
b = a+b;
|
||
d = a+b;
|
||
}
|
||
else{
|
||
d = a+c;
|
||
y = b+d;
|
||
}
|
||
let x = a+b;
|
||
y = c + d;
|
||
return x;
|
||
}
|
||
|
||
```
|
||
|
||
我也把答案写出来了,看看跟你想的是否一样。在整个代码优化完毕以后,其实只剩下很少的代码了。变量c、d和y的定义都被优化掉了。
|
||
|
||
```plain
|
||
function deadCode2(b:number,c:number){
|
||
let a:number = b+c;
|
||
if (b > 0){
|
||
b = a+b;
|
||
}
|
||
let x = a+b;
|
||
return x;
|
||
}
|
||
|
||
```
|
||
|
||
这个例子其实是我在《编译原理之美》第28节中举的一个例子。在那里,我是基于CFG做变量活跃性分析,再基于分析结果去做优化。你有兴趣的话可以去看一下。那个算法的核心,是跨越多个基本块做变量活跃性分析。一个基本块的输出,会顺着控制流,成为另一个基本块的输入。在这门课的第20节,我也介绍过这种变量活跃性分析的思路,所以这里我就不再去重复了。
|
||
|
||
那在这节课中,我们感兴趣的是,**基于现在的IR,我们能否更便捷地实现变量活跃性分析,实现死代码的删除呢?**
|
||
|
||
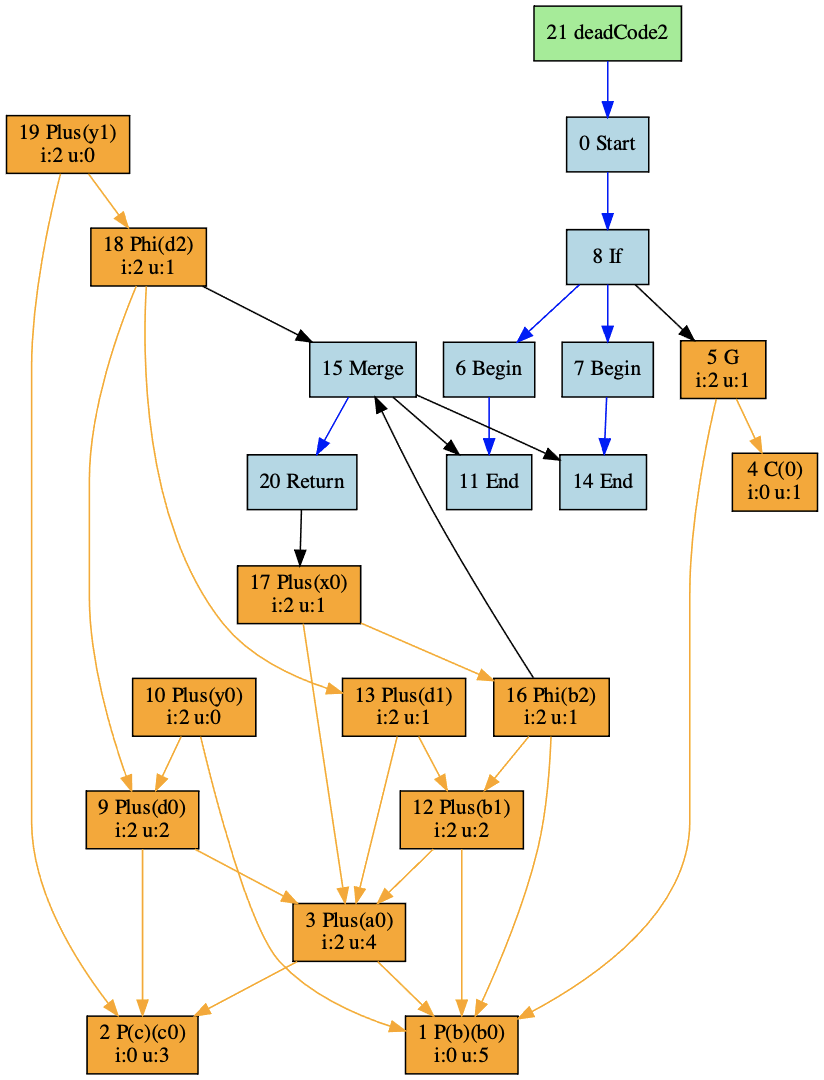
我们先来运行一下“node play example\_opt2.ts --dumpIR”命令,看一下deadCode2函数对应的IR是什么样子的。
|
||
|
||
|
||
|
||
你会发现,这个图里加入了If节点,并产生了流程分支,然后又通过Merge节点合并到了一起,不同流程分支的变量产生了多个定义。相应的,IR中也有Phi节点,用来选择不同流程分支的变量定义。
|
||
|
||
以变量d为例,实际上现在我们的程序保存了d的三个定义,在if块中定义了d0,在else块中定义了d1,“y = c + d”这一句中还有一个。不过在“y = c + d”这一句中的变量d,要通过phi节点来获得。类似的,变量b也有三个定义,而变量y也有两个不同的定义。
|
||
|
||
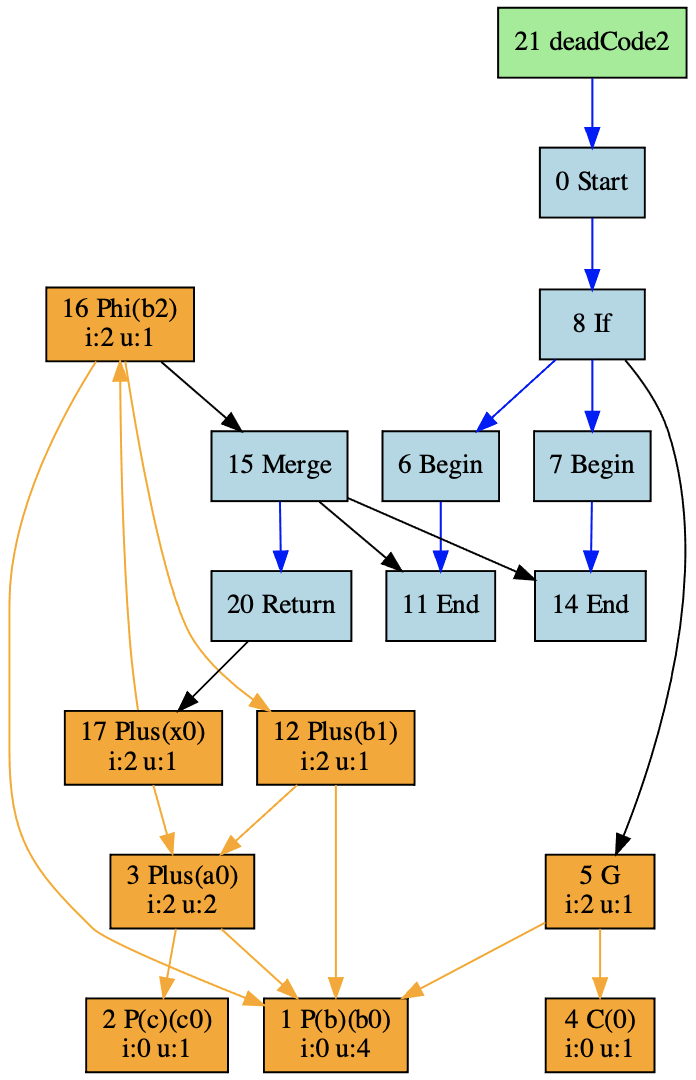
同时,你还会发现,图中有几个节点的uses属性为空集合。比如y0和y1,所以我们又可以把它们从图中去掉。而在去掉了y0和y1以后,d0、d1和d2也不再有用,所以也可以去掉。做过这些优化以后,IR图就变成了下面的样子:
|
||
|
||
|
||
|
||
而最后这个版本,其实就可以对应上优化后的那个源代码了。
|
||
|
||
所以,我们在全局做死代码的删除,其实跟前一节课的本地优化没有区别,都是**根据uses属性来做判断**。**因为这个时候,控制流并没有影响我们的优化算法。**
|
||
|
||
不过,并不是在所有情况下,控制流都不会影响到优化。我们再来分析一种优化技术,就是部分冗余消除。在这个场景下,控制流的影响就会体现出来。
|
||
|
||
## 部分冗余消除(PRE)
|
||
|
||
我们之前讨论过公共子表达式删除(CSE),说的是如果两个表达式有公共的子表达式,那么这个子表达式可以只计算一次。
|
||
|
||
在全局优化中有一种类似的情况,两个表达式中也存在公共子表达式,但是它们位于不同的流程分支,这种情况下我们可以使用**部分冗余消除算法**。
|
||
|
||
部分冗余消除(Partial Redundancy Elimination,PRE),是公共子表达式消除的一种特殊情况。我这里用了一个来自[wikipedia](https://time.geekbang.org/column/article/248770#:~:text=%E6%AF%94%E5%A6%82%EF%BC%8C%E8%BF%99%E4%B8%AA%E6%9D%A5%E8%87%AA-,Wikipedia,-%E7%9A%84%E4%BE%8B%E5%AD%90%E4%B8%AD)的例子,这个程序里一个分支有“x+4”这个公共子表达式,而另一个分支则没有。
|
||
|
||
你用肉眼就可以看出,这个例子优化得不够好的地方,比如,如果some\_condition为true,那么x+4这个子表达式就要计算两次:
|
||
|
||
```plain
|
||
if (some_condition) {
|
||
// some code that does not alter x
|
||
y = x + 4;
|
||
}
|
||
else {
|
||
// other code that does not alter x
|
||
}
|
||
z = x + 4;
|
||
|
||
```
|
||
|
||
这些代码经过优化以后,可以改成下面这样。当some\_condition为true的时候,x+4也只需要计算一次:
|
||
|
||
```plain
|
||
if (some_condition) {
|
||
// some code that does not alter x
|
||
t = x + 4;
|
||
y = t;
|
||
}
|
||
else {
|
||
// other code that does not alter x
|
||
t = x + 4;
|
||
}
|
||
z = t;
|
||
|
||
```
|
||
|
||
这个时候,两个条件分支里都有t = x+4这个语句,那我们还可以把它提到外面去,让生成的代码更小一点:
|
||
|
||
```plain
|
||
t = x + 4;
|
||
if (some_condition) {
|
||
// some code that does not alter x
|
||
y = t;
|
||
}
|
||
else {
|
||
// other code that does not alter x
|
||
}
|
||
z = t;
|
||
|
||
```
|
||
|
||
如果用我们的IR对这个例子进行优化,也很容易实现。我们先把这个wikipedia的例子用TypeScript改写一下:
|
||
|
||
```plain
|
||
function PRE(x:number):number{
|
||
let y:number = 0;
|
||
if (x>0){
|
||
y = x+4;
|
||
}
|
||
let z = x+4;
|
||
return y+z;
|
||
}
|
||
|
||
```
|
||
|
||
然后再生成它的IR看一下:
|
||
|
||
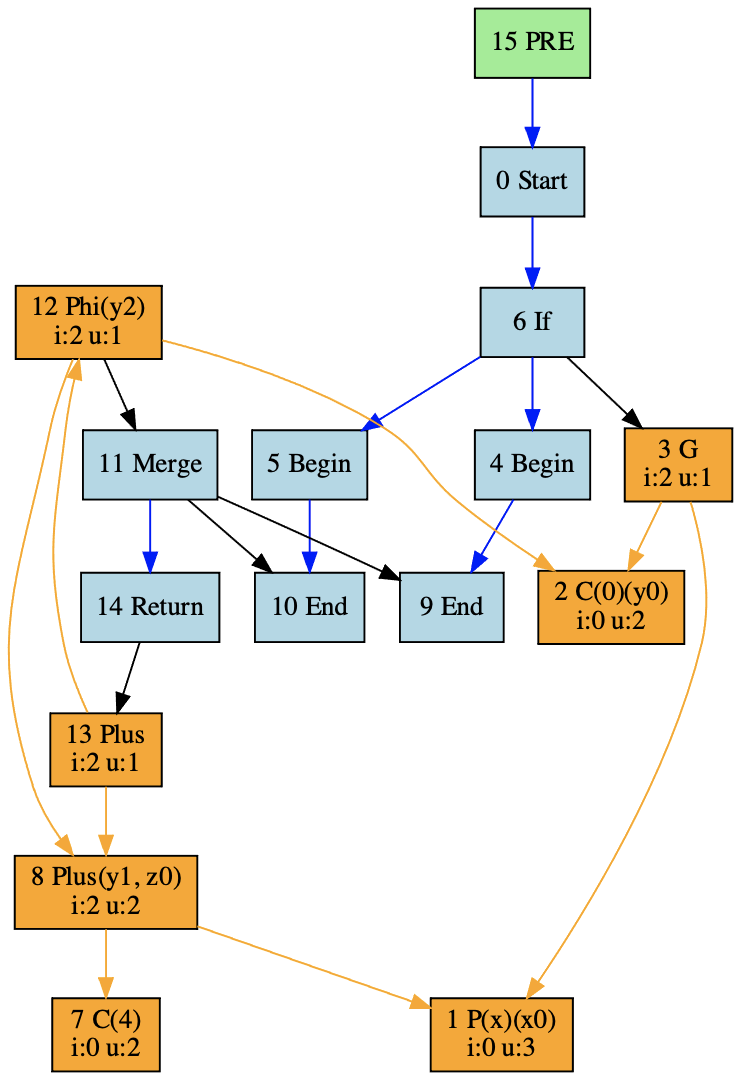
|
||
|
||
从这个IR中你能看到,x+4对应着编号为8的节点,y1和z的值都是x+4,最后的返回值是13号节点,也就是y2+z。而y2是一个phi节点,根据流程分支,它的值可能是常量0,也可能是x+4。
|
||
|
||
我们再进一步,如果你研究13号节点的def链,你会发现它肯定会依赖到8号节点,也就是x+4。无论程序是否经过if语句的那条控制流,都会是这样。所以,当我们把节点划分到基本块的时候,8号节点可以划分到if语句之前的基本块,这样就实现了对x+4只计算一次的目的。相当于下面的代码:
|
||
|
||
```plain
|
||
function PRE(x:number):number{
|
||
let y:number = 0;
|
||
let t = x+4;
|
||
if (x>0){
|
||
y = t;
|
||
}
|
||
let z = t;
|
||
return y+z;
|
||
}
|
||
|
||
```
|
||
|
||
从这个例子你能看出来,其实基于我们的IR,数据流的计算总能达到最节省计算量的效果。**那么在全局优化中,重点其实就变成了如何把不同的数据节点划分到不同的基本块中**。就像刚才,我们可以把x+4计算放在if语句中,也可以放在外面。在某些情况下,这种不同的划分会影响到程序的性能。
|
||
|
||
所以,接下来我们就讨论一下如何划分基本块,并进行指令的调度。
|
||
|
||
## 划分基本块和指令调度(Schedule)
|
||
|
||
我们当前的IR采用的是一个基于图的数据结构。可是我们在生成汇编代码的时候,还是要把整个程序划分成基本块,并在基本块之间实现跳转。这个时候,我们就要采用一个调度算法,确定把哪条代码放到哪个基本块。
|
||
|
||
划分基本块其实比较简单,我们基于控制流做运算就行了。每产生一个控制流分支的时候,我们就划分一个新的基本块。比如,我们刚才的PRE示例程序就可以划分成四个基本块,if语句前后各有一个,而if语句的两个分支也分别是一个基本块。
|
||
|
||
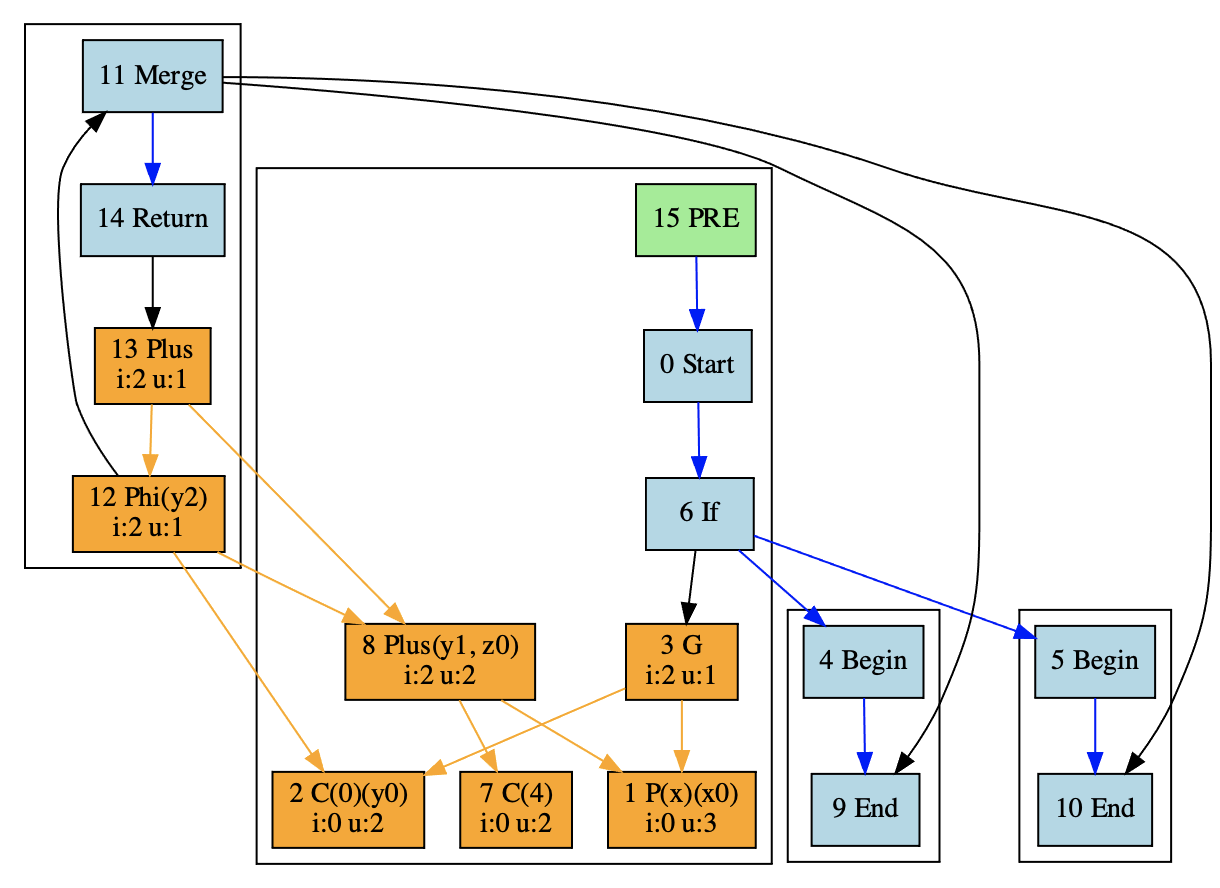
|
||
|
||
接下来,我们就要把各个数据流节点也纳入到不同的基本块中去。由于数据节点是浮动的,它其实有比较大的自由度,可以归到不同的基本块中去。**那我们这里的算法,就是如果某个表达式的计算会出现在多个流程分支里,我们就尽量把它提到外面去**。比如对x+4的计算,我们就把它放到第1个基本块中了。
|
||
|
||
那看着前面这张图,你可能会产生疑问:难道if条件的两个流程分支都是空的基本块吗?按照源代码,在x>0的时候,应该有一个y=t的赋值呀?
|
||
|
||
没错,我们现在把控制流的Merge节点和数据流的Phi节点都归到了第4个基本块。但其实phi节点会在Merge节点之前的两个基本块中生成代码的。只不过是因为,我们现在在HIR的阶段,只能画成这样,没法把phi节点划分到前面两个不同的基本块去。在生成LIR或汇编代码的时候,phi节点就会被转化成位于基本块中的代码。所以,这个阶段,我们只需要记住phi节点生成代码的特点就行了。
|
||
|
||
看到这里,我相信你已经基本了解如何划分基本块和做代码调度了。其实,在这里讨论这些,我是为了引出下一个全局优化,也就是循环无关代码外提。
|
||
|
||
## 循环无关代码外提(LICM)
|
||
|
||
我们在第36节课曾经讨论锅一个循环无关代码外提(Loop-Invariant Code Motion,LICM)的例子。在这个例子中,变量c的定义是与循环无关的,却被放到了循环的内部,导致每次循环都要计算一遍a\*a:
|
||
|
||
```plain
|
||
function LICM(a:number):number{
|
||
let b = 0;
|
||
for (let i = 0; i< a; i++){
|
||
let c = a*a; //变量c的值与循环无关,导致重复计算!
|
||
b = i + c;
|
||
}
|
||
return b;
|
||
}
|
||
|
||
```
|
||
|
||
所以,理想的优化结果,就是这行代码提到循环的外面。这样,a\*a的值只需要计算一次就行了:
|
||
|
||
```plain
|
||
function LICM(a:number):number{
|
||
let b = 0;
|
||
let c = a*a; //外提
|
||
for (let i = 0; i< a; i++){
|
||
b = i + c;
|
||
}
|
||
return b;
|
||
}
|
||
|
||
```
|
||
|
||
当然,这么做也有一个风险,就是如果程序并不进入循环,那么这次计算就白做了,反倒多消耗了计算量。不过,这个情况总归是小概率事件。除非我们有运行时的统计数据作依托,不然我们很难做出更准确地选择。
|
||
|
||
在静态编译的情况下,我们只能假设把它放到循环外面,大概率是比放在循环里面更好一些。从这个场景中,你也能再次体会到“全生命周期优化”的意义,**AOT编译并不总是能得到最好的效果**。
|
||
|
||
那要如何实现这个优化呢?我们还是把这个程序生成IR来看一下:
|
||
|
||
|
||
|
||
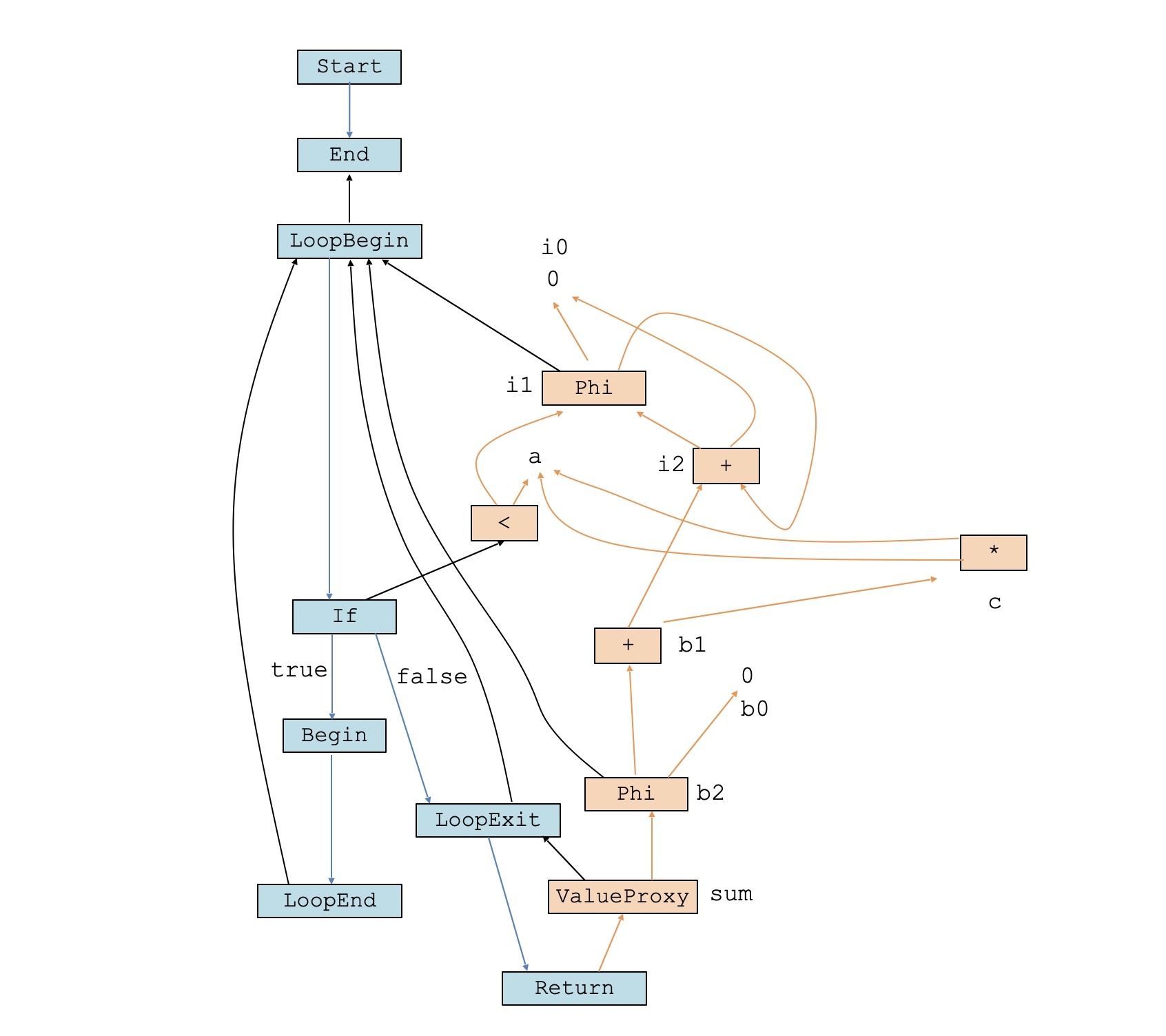
从这个IR图中,我们能看出a\*a计算确实是与循环无关的,是可以在循环内部和外部浮动的。相比之下,变量i和b1的计算,则受限于控制流的结构,只能出现在LoopBegin之后。
|
||
|
||
所以,基于我们的指令调度算法,我们就把a\*a这个节点归入第1个基本块,这样就实现了循环无关代码的外提。
|
||
|
||
## 课程小结
|
||
|
||
好了,这就是今天这节课全部的内容了。这节课里,我们讨论了在全局做优化会涉及的的一些技术点,包括:
|
||
|
||
首先,在SSA格式下,变量可以产生多个定义。在生成IR的过程中,我们要把每个变量定义跟产生它的控制流相关联,这样我们在数据流中引用变量的时候,就能找到正确的定义了。
|
||
|
||
第二,在全局死代码删除的时候,我们只需要考虑数据节点的属性就行,也就是看uses属性是否为空就好了。这跟在一个基本块中做死代码删除没有区别。
|
||
|
||
第三,在全局做公共子表达式删除的时候,我们会遇到部分冗余消除的优化场景。基于我们当前的IR,可以保证公共子表达式只计算一次。
|
||
|
||
第四,在全局优化中,我们需要考虑把数据节点放到哪个基本块中,这叫做指令调度。在有些场景下,比如循环无关代码外提,把指令划分到不同的基本块会导致不同的性能。在AOT编译时,我们通常总是把循环无关的代码提到循环外面。
|
||
|
||
## 思考题
|
||
|
||
我们这两节课分析了不少优化算法,不知道你还有没有了解过其他优化算法?它们在我们的IR中是否也很容易实现呢?比如,我在《编译原理实战课》的第07讲,提到了很多优化算法。我建议你研究一下全局值编号(GVN)和代码提升(Code Hoisting)在我们的IR上如何实现。欢迎在留言区分享你的发现。
|
||
|
||
欢迎你把这节课分享给更多感兴趣的朋友。我是宫文学,我们下节课见。
|
||
|
||
## 资源链接
|
||
|
||
这节课的示例代码目录在[这里](https://gitee.com/richard-gong/craft-a-language/tree/master/39-40),主要看[ir.ts](https://gitee.com/richard-gong/craft-a-language/blob/master/39-40/ir.ts)。
|
||
|