393 lines
23 KiB
Markdown
393 lines
23 KiB
Markdown
# 20|怎么实现一个更好的寄存器分配算法:实现篇
|
||
|
||
你好,我是宫文学。
|
||
|
||
在上一节课,我们已经介绍了寄存器分配算法的原理。不过呢,我们这门课,不是停留在对原理的理解上就够了,还要把它具体实现出来才行。在实现的过程中,你会发现有不少实际的具体问题要去解决。而你一旦解决好了它们,你对寄存器分配相关原理的理解也会变得更加通透和深入。
|
||
|
||
所以,今天这一节课,我就会带你具体实现寄存器分配算法。在这个过程中,你会解决这些具体的技术问题:
|
||
|
||
* 首先,我们会了解如何基于我们现在的LIR来具体实现变量活跃性分析。特别是,当程序中存在多个基本块的时候,分析算法该如何设计。
|
||
* 第二,我们也会学习到在实现线性扫描算法中的一些技术点,包括如何分配寄存器、在调用函数时如何保存Caller需要保护的寄存器,以及如何正确的维护栈桢。
|
||
|
||
解决了这些问题之后,我们会对我们的语言再做一次性能测试,看看这次性能的提升有多大。那么接下来,就让我们先看看实现变量活跃性分析,需要考虑哪些技术细节吧。
|
||
|
||
## 实现变量活跃性分析
|
||
|
||
我们先来总结一下,在实现变量活跃性分析的时候,我们会遇到哪几个技术点。我们一般要考虑如何保存变量活跃性分析的结果、如何表达变量的定义,以及如何基于CFG来做变量活跃性分析这三个方面。
|
||
|
||
现在我们就一一来分析一下。
|
||
|
||
首先,我们要设计一个数据结构,把活跃性分析的结果保存下来,方便我们后面在寄存器分配算法中使用。
|
||
|
||
这个数据结构很简单,我们使用一个Map即可。这个Map的key是指令,而value是一个数组,也就是执行当前指令时,活跃变量的集合。
|
||
|
||
```plain
|
||
liveVars:Map<Inst, number[]> = new Map();
|
||
|
||
```
|
||
|
||
确定了数据结构以后,我们再讨论一下算法的实现。在算法的执行过程中呢,我们倒着扫描一条条指令。对于每条指令,我们要分析它的操作数。如果操作数是一个变量下标,那我们就把这个变量加到活跃变量的集合中。所以,往集合里加变量实现起来很简单。
|
||
|
||
可是,从集合里减变量就不那么简单了。为什么呢?根据我们上一节课讲过的算法,我们需要在变量声明的时候,把这个变量从集合里去掉。可是,我们当前的LIR中并没有记录哪个变量是在什么时候声明的,也就没办法知道变量的生存期是从什么时候开始的了。
|
||
|
||
那怎么来解决这个问题呢?我的办法是,向LIR里再加一条指令,这条指令专门用来指示变量的声明。我把这条指令的OpCode叫做[declVar](https://gitee.com/richard-gong/craft-a-language/blob/master/20/asm_x86-64.ts#L126)。
|
||
|
||
由于这条指令并不能转化成具体的可执行的指令,所以你可以把它叫做伪指令。它仅用于我们的寄存器分配算法。
|
||
|
||
好了,在加入了这条指令以后,我们就能对一个基本块进行变量活跃性分析了。具体实现你可以参考代码LivenessAnalyzer,其中的核心逻辑我放在下面了:
|
||
|
||
```plain
|
||
//为每一条指令计算活跃变量集合
|
||
for (let i = bb.insts.length - 1; i >=0; i--){
|
||
let inst = bb.insts[i];
|
||
if (inst.numOprands == 1){
|
||
let inst_1 = inst as Inst_1;
|
||
//变量声明伪指令,从liveVars集合中去掉该变量
|
||
if (inst_1.op == OpCode.declVar){
|
||
let varIndex = inst_1.oprand.value as number;
|
||
let indexInArray = vars.indexOf(varIndex);
|
||
if (indexInArray != -1){
|
||
vars.splice(indexInArray,1);
|
||
}
|
||
}
|
||
//查看指令中引用了哪个变量,就加到liveVars集合中去
|
||
else{
|
||
this.updateLiveVars(inst_1, inst_1.oprand, vars);
|
||
}
|
||
}
|
||
else if (inst.numOprands == 2){
|
||
let inst_2 = inst as Inst_2;
|
||
this.updateLiveVars(inst_2, inst_2.oprand1, vars);
|
||
this.updateLiveVars(inst_2, inst_2.oprand2, vars);
|
||
}
|
||
|
||
result.liveVars.set(inst, vars);
|
||
vars = vars.slice(0); //克隆一份,用于下一条指令
|
||
}
|
||
|
||
```
|
||
|
||
我们可以用这个算法跑一个例子看看,这个例子是上一节课的示例程序的前半截:
|
||
|
||
```plain
|
||
function foo(p1:number,p2:number,p3:number,p4:number,p5:number,p6:number){
|
||
let x7 = p1;
|
||
let x8 = p2;
|
||
let x9 = p3;
|
||
let x10 = p4;
|
||
let x11 = p5;
|
||
let x12 = p6 + x7 + x8 + x9 + x10 + x11;
|
||
let sum = x12;
|
||
return sum;
|
||
}
|
||
|
||
```
|
||
|
||
你可以运行node play example\_reg.ts -v --dumpAsm来显示分析的结果。我把终端的输出放到下面了。你能看到,每个语句对应的活跃变量集合,跟我们前一节的分析是吻合的。也证明我们的实现是正确的。
|
||
|
||
```plain
|
||
function: foo
|
||
bb:LBB0
|
||
[ 5, 4, 3, 2, 1, 0 ]
|
||
declVar var6
|
||
[
|
||
6, 5, 4, 3,
|
||
2, 1, 0
|
||
]
|
||
movl var0, var6
|
||
[ 6, 5, 4, 3, 2, 1 ]
|
||
declVar var7
|
||
[
|
||
7, 6, 5, 4,
|
||
3, 2, 1
|
||
]
|
||
movl var1, var7
|
||
[ 7, 6, 5, 4, 3, 2 ]
|
||
declVar var8
|
||
[
|
||
8, 7, 6, 5,
|
||
4, 3, 2
|
||
]
|
||
movl var2, var8
|
||
[ 8, 7, 6, 5, 4, 3 ]
|
||
declVar var9
|
||
[
|
||
9, 8, 7, 6,
|
||
5, 4, 3
|
||
]
|
||
movl var3, var9
|
||
[ 9, 8, 7, 6, 5, 4 ]
|
||
declVar var10
|
||
[
|
||
10, 9, 8, 7,
|
||
6, 5, 4
|
||
]
|
||
movl var4, var10
|
||
[ 10, 9, 8, 7, 6, 5 ]
|
||
declVar var13
|
||
[
|
||
13, 10, 9, 8,
|
||
7, 6, 5
|
||
]
|
||
movl var5, var13
|
||
[ 13, 10, 9, 8, 7, 6 ]
|
||
addl var6, var13
|
||
[ 13, 10, 9, 8, 7 ]
|
||
addl var7, var13
|
||
[ 13, 10, 9, 8 ]
|
||
addl var8, var13
|
||
[ 13, 10, 9 ]
|
||
addl var9, var13
|
||
[ 13, 10 ]
|
||
addl var10, var13
|
||
[ 13 ]
|
||
declVar var11
|
||
[ 11, 13 ]
|
||
movl var13, var11
|
||
[ 11 ]
|
||
declVar var12
|
||
[ 12, 11 ]
|
||
movl var11, var12
|
||
[ 12 ]
|
||
movl var12, returnSlot
|
||
[]
|
||
|
||
```
|
||
|
||
可是,这个例子中仅有一个基本块,所以我们的算法只需要把这个基本块的代码从下往上扫描一遍就行了。
|
||
|
||
可如果存在多个基本块,该如何处理呢?比如,我们如果在示例程序中加入循环语句以后,就会产生不止一个基本块了。难道我们只需要把每个基本块分别做一下分析就可以了吗?
|
||
|
||
不是的。当存在多个基本块的时候,基本块之间的关系会形成一个CFG,也就是控制流图。一个基本块的活跃变量的情况,会影响它前序的基本块的变量活跃性分析结果。这里我们具体展开来看一下。
|
||
|
||
## 基于CFG的变量活跃性分析
|
||
|
||
在前面几节课,我们讲到if语句和for循环语句的时候,说到它们的执行流程可以用一个CFG来表示。我借用了之前我在[《编译原理之美》](https://time.geekbang.org/column/intro/100034101)课程中用过的一个例子,来和你说明一下如何基于CFG来做数据流分析。
|
||
|
||
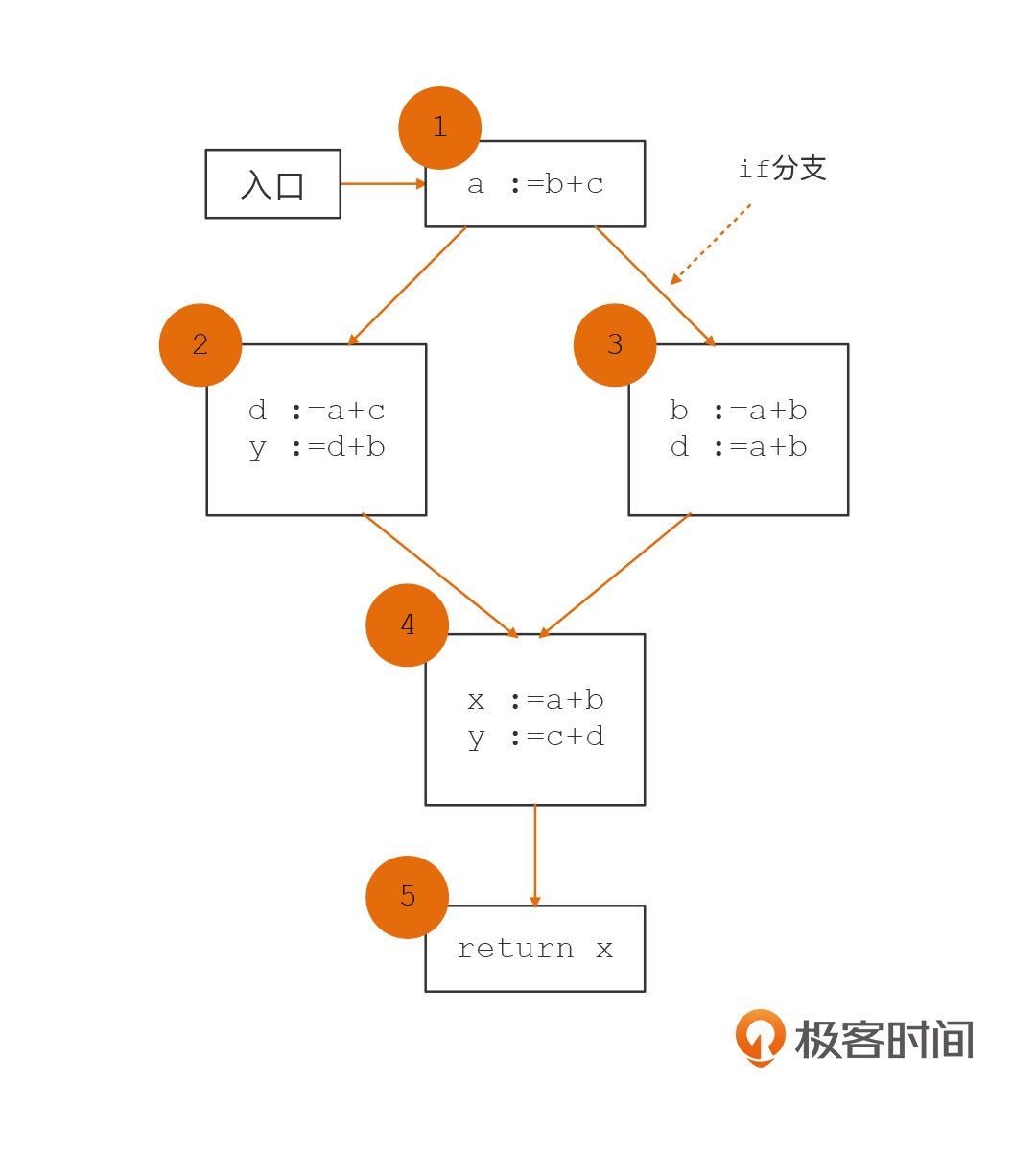
我们先来看第一个图,这是一个带有if分支的CFG。这个CFG里,每个基本块都编了号。
|
||
|
||
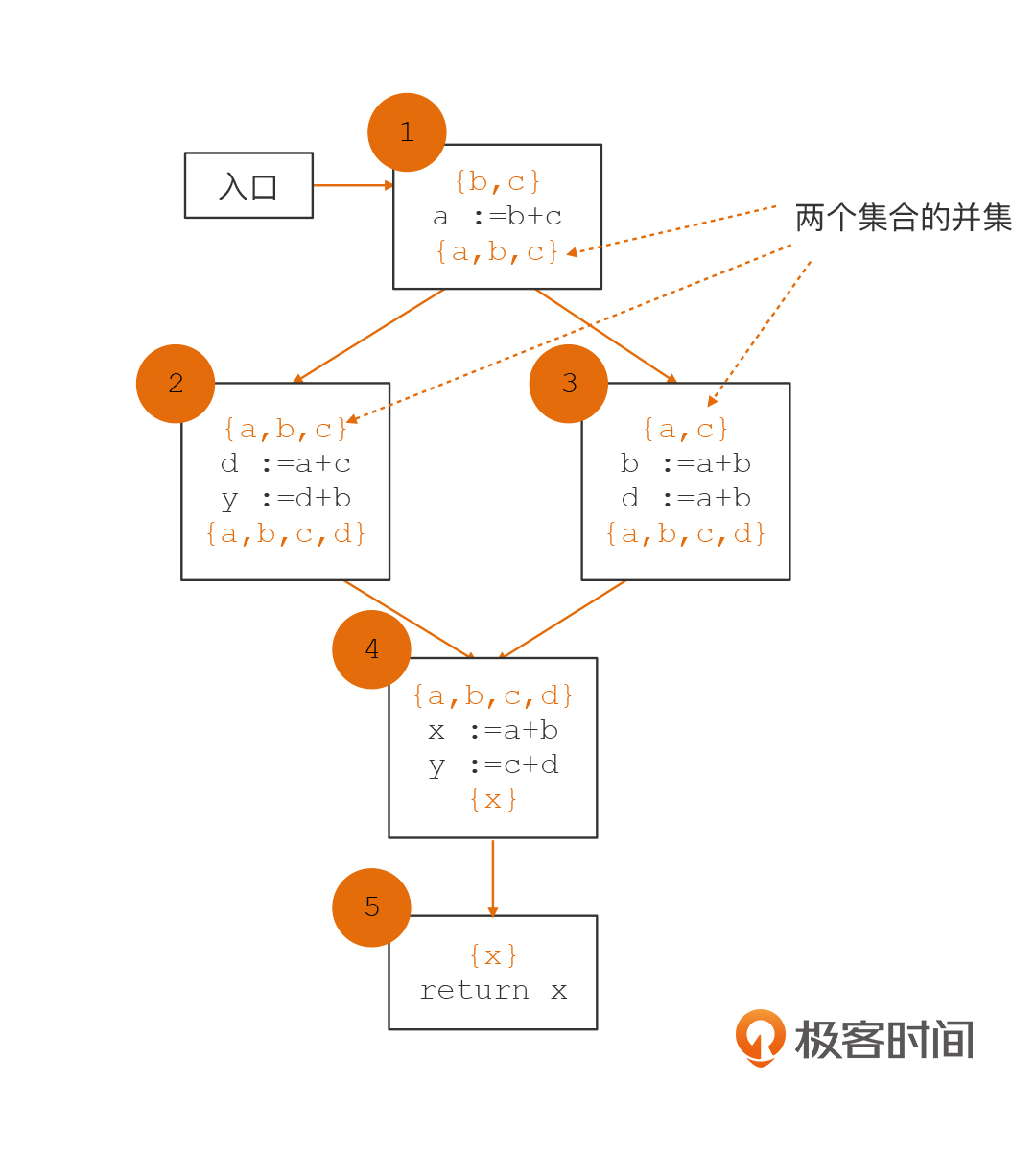
在进行变量活跃性分析的时候,根据我们上一节课提到过的由下到上的顺序,我们需要倒着从第5个基本块进行分析。你会看到,第5个基本块需要活跃变量x,这就形成了对基本块4的需求。所以,我们知道了,基本块4一开始的活跃变量集合不是空集,而是{x}。
|
||
|
||
再进一步,基本块4又形成了对2和3的需求,要求它们提供{a,b,c,d}共4个活跃变量。
|
||
|
||
依次类推,基本块2和3又形成了对基本块1的需求,要求基本块1提供{a,b,c}共3个活跃变量。
|
||
|
||
到这就完事了。这看上去也不复杂呀,就是沿着CFG中的边,逆向遍历一遍图就行了呗!
|
||
|
||
慢着,我们刚刚举的例子只是一个比较简单的情况。在这个例子中,图里没有形成环,是个有向无环图,是图的数据结构中几乎最简单的一种,算法处理比较容易。但是我们实际的程序,会形成更复杂的图。比如,for循环语句就会形成带有环的图,使得里面的基本块形成循环依赖,这会导致算法复杂度的提升。
|
||
|
||
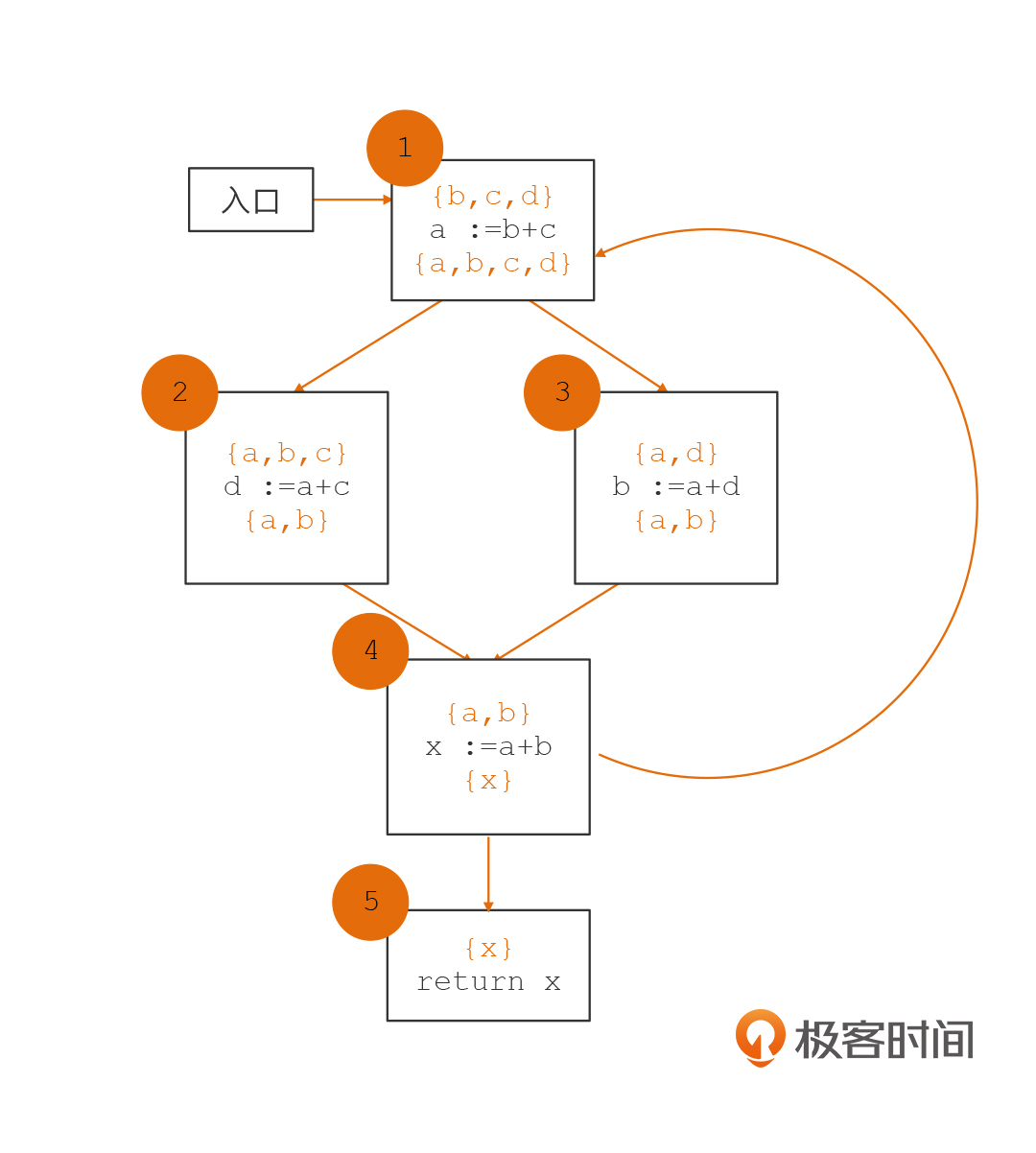
我们接着来看看下面的例子,这个例子中我们增加了从基本块4到1的控制流,从而构成了环路。我们还是沿着刚才的计算顺序,分别计算基本块5->4->3->2->1,这会形成下面的活跃变量集合。
|
||
|
||
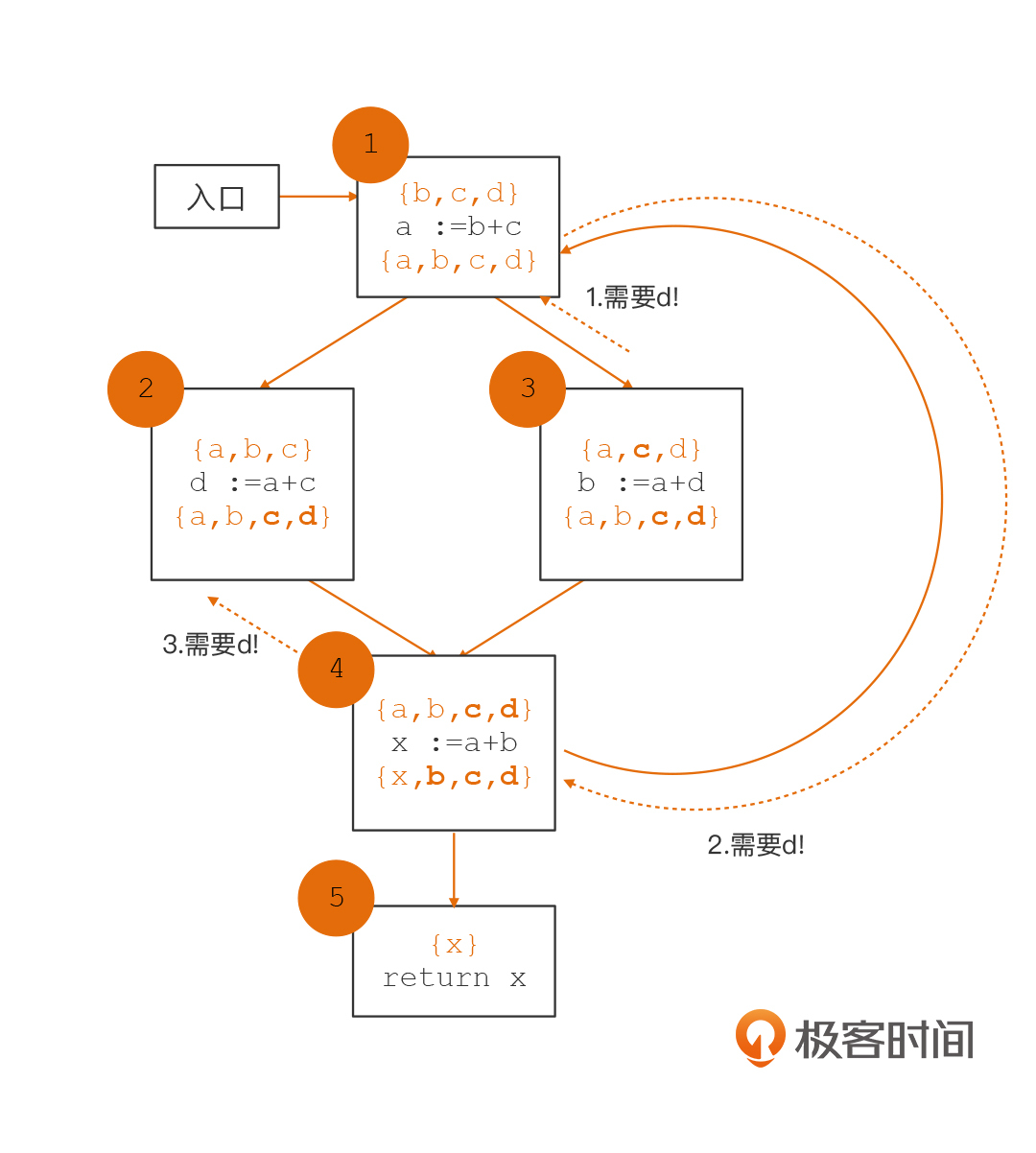
但是,这并没有计算完毕。你看,由于存在着从4到1的环路,所以1的输出,会形成对4的活跃变量的需求。所以,我们这里又要重新计算一遍基本块4的活跃变量,进而导致我们需要对基本块3、2和1都再次计算一遍,引起它们的活跃变量集合的变化。
|
||
|
||
这样的循环可能会重复多次,直到每个基本块的活跃变量集合不再有变化为止。
|
||
|
||
上面这些就是我们对基于CFG的变量活跃性分析的算法思路的分析。你会看到,它比针对单个基本块的分析确实复杂了不少,接下来就让我们实现一下吧。
|
||
|
||
**首先,我们要对数据结构做一个调整。**在这部分,我们需要记录下每个基本块初始的活跃变量集合。这个集合可能不再是一个空集,因为后序基本块可能要求前序基本块必须提供某些活跃变量。
|
||
|
||
所以,我们要记下每个基本块初始的活跃变量集合。在打印活跃变量的时候,把这个初始的集合显示在最下面。
|
||
|
||
```plain
|
||
/**
|
||
* 变量活跃性分析的结果
|
||
*/
|
||
class LivenessResult{
|
||
liveVars:Map<Inst, number[]> = new Map();
|
||
initialVars:Map<BasicBlock, number[]> = new Map();
|
||
}
|
||
|
||
```
|
||
|
||
**第二,我们要为每个函数构建CFG。**当前,每个函数里已经保存了一些基本块,但它们并没有表达成直观的CFG。比如,我们现在还没有简单的方法知道每个基本块都有哪些前序基本块和后续基本块。因此,我们专门设计一个CFG的类,来体现图的数据结构。
|
||
|
||
```plain
|
||
class CFG{
|
||
//基本块的列表。第一个和最后一个BasicBlock是图的root。
|
||
bbs:BasicBlock[];
|
||
|
||
//每个BasicBlock输出的边
|
||
edgesOut:Map<BasicBlock, BasicBlock[]>=new Map();
|
||
|
||
//每个BasicBlock输入的边
|
||
edgesIn:Map<BasicBlock,BasicBlock[]> = new Map();
|
||
...
|
||
}
|
||
|
||
```
|
||
|
||
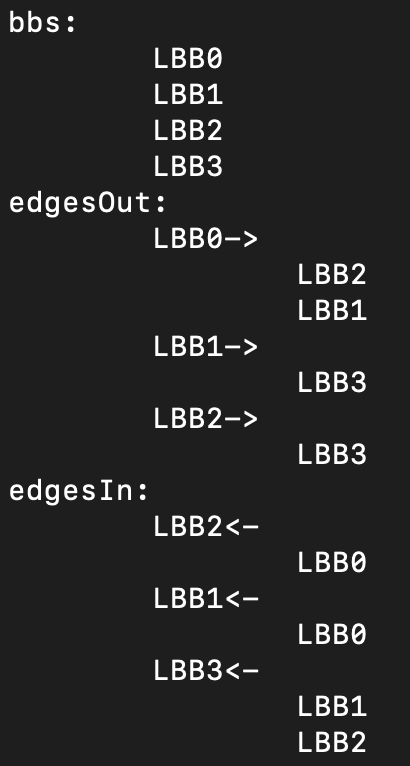
在这个CFG类中,有两个Map很有用。一个Map记录了所有进入某个基本块的边,另一个Map则记录了从该基本块到其他基本块的边。通过这两个Map,我们可以很容易地沿着这些边进行正向或逆向的遍历。
|
||
在这里,我们通过了一个专门的buildCFG方法来构建CFG。如果你用node play example\_if.ts -v --dumpAsm命令,可以打印出为每个函数构建的CFG出来。 我附了一张截图:
|
||
|
||
|
||
|
||
**第三,我们实现要实现基于CFG的活跃变量分析算法。**这个算法的思路,是逆向遍历整个CFG,而且只要某个基本块的分析结果会影响到前序的基本块,那我们就需要持续不停地进行迭代分析,直到每个基本块的活跃变量集合都不再变化为止。
|
||
|
||
我放了一块比较关键的代码,具体实现你可以参考代码库中的[analyzeFunction](https://gitee.com/richard-gong/craft-a-language/blob/master/20/asm_x86-64.ts#L1809)方法。
|
||
|
||
```plain
|
||
//持续遍历图,直到没有BasicBlock的活跃变量需要被更新
|
||
let bbsToDo:BasicBlock[] = bbs.slice(0);
|
||
while (bbsToDo.length>0){
|
||
let bb = bbsToDo.pop() as BasicBlock;
|
||
this.analyzeBasicBlock(bb, result);
|
||
//取出第一行的活跃变量集合,作为对前面的BasicBlock的输入
|
||
let liveVars = bb.insts.length == 0? [] : (result.liveVars.get(bb.insts[0]) as number[]);
|
||
let fromBBs = cfg.edgesIn.get(bb);
|
||
if (typeof fromBBs != 'undefined'){
|
||
for (let bb2 of fromBBs){
|
||
let liveVars2 = result.initialVars.get(bb2) as number[];
|
||
//如果能向上面的BB提供不同的活跃变量,则需要重新分析bb2
|
||
if (!this.isSubsetOf(liveVars, liveVars2)){
|
||
if (bbsToDo.indexOf(bb2) == -1)
|
||
bbsToDo.push(bb2);
|
||
let unionVars = this.unionOf(liveVars, liveVars2);
|
||
result.initialVars.set(bb2, unionVars);
|
||
}
|
||
}
|
||
}
|
||
}
|
||
|
||
```
|
||
|
||
这里你仍然可以用node play example\_if.ts -v --dumpAsm命令来显示分析后的结果。
|
||
|
||
好了,在实现了基于CFG的分析算法以后,现在我们已经彻底完成了变量活跃性分析。接下来,就是具体实现线性扫描算法了!
|
||
|
||
## 实现线性扫描算法
|
||
|
||
根据我们上节课原理篇的安排,在原来的简单寄存器分配算法的基础上,我们要进行一些调整,把它改成线性扫描算法。
|
||
|
||
**第一个重要的技术点,也是其中****最主要的修改,是对lowerOprand方法的修改。**在这个方法中,我们会把变量下标类型的操作数(也就是逻辑寄存器)映射成物理寄存器。
|
||
|
||
在lowerOprand方法中,我们会调用[getFreeRegister](https://gitee.com/richard-gong/craft-a-language/blob/master/20/asm_x86-64.ts#L1582)方法来获取一个寄存器。在这个方法里呢,算法会首先试图复用已分配过的寄存器,也就是检查现在已经被分配了寄存器的变量,看看现在哪个变量的生存期已经结束了,这样就可以腾出这个寄存器来了。
|
||
|
||
如果没有可复用的寄存器,那么就需要从未分配的寄存器里分配出一个来。那如果所有寄存器都用完了呢?
|
||
|
||
这个时候,我们就需要溢出(Spill)一个现成的寄存器。我们现在溢出寄存器的算法比较简单,只要找到第一个可用的寄存器,就把它溢出就好了。
|
||
|
||
**第二个重要的技术点,是在调用函数的前后,要对寄存器做保护和重载。**对寄存器做保护,实际上就是把它溢出到内存中就可以了,等函数调用完毕,我们再把它们从内存加载到寄存器里来。这里你可以参考spillVar和reloadVar方法。
|
||
|
||
这里还有个技术细节要讨论一下。在调用函数的时候,我们到底需要保护哪些寄存器呢?这个是需要计算一下的,我们这里还是要利用变量活跃性分析的结果,也就是函数调用时的活跃变量。
|
||
|
||
但是,如果在调用\_foo前后,变量活跃性集合是不同的,我们应该以哪个集合为准呢?你可以看看下面的例子,并思考一下。
|
||
|
||
```plain
|
||
[x1, x2, x3]
|
||
foo(x1);
|
||
[x2, x3]
|
||
|
||
```
|
||
|
||
答案是函数调用之后的活跃变量集合。因为在例子中,x1作为参数使用过以后,后面就不再用它了,所以就没有必要保护它的值了。
|
||
|
||
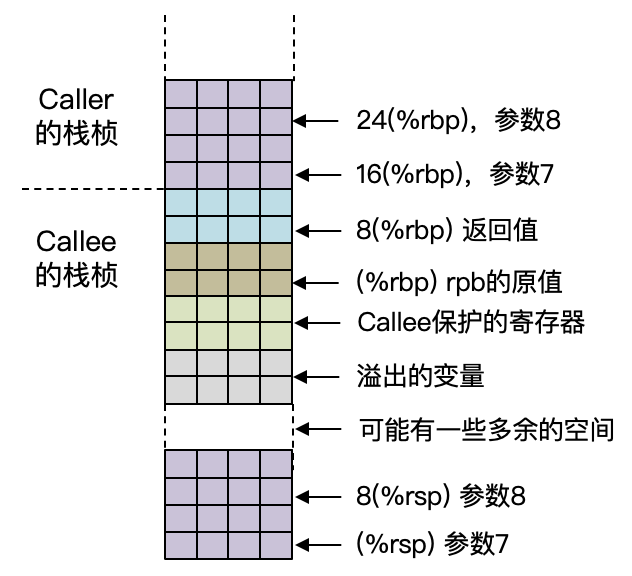
**第三个重要的技术点,就是栈桢的维护。**采用新的寄存器分配算法以后,我们栈桢的内容会有所不同。这个时候了,我们就没有必要再在内存里逐个保存参数和本地变量了,而是只为溢出的变量提供空间就可以了。
|
||
|
||
我们以这张图为例分析一下:
|
||
|
||
|
||
|
||
这里栈帧维护的重点,是要能够准确计算出每个被溢出的变量的地址相对于rbp的偏移量。
|
||
|
||
而这里就有一个不确定的因素了,就是在溢出变量的存储空间上部,是为Callee保护的寄存器而留出的空间。但是我们到底需要保存几个Callee保护的寄存器,这要在寄存器分配算法执行完毕以后才能知道。
|
||
|
||
所以你会看到,所有被Spill的变量的准确内存地址,是需要在算法的最后调整一次的。你可以看一下lowerFunction中的这段代码:
|
||
|
||
```plain
|
||
//把spilledVars中的地址修改一下,加上CalleeProtectedReg所占的空间
|
||
if (this.usedCalleeProtectedRegs.length >0){
|
||
let offset = this.usedCalleeProtectedRegs.length*8;
|
||
for (let address of this.spilledVars2Address.values()){
|
||
let oldValue = address.value as number;
|
||
address.value = oldValue+offset;
|
||
}
|
||
}
|
||
|
||
```
|
||
|
||
好了,关于各种技术实现的细节,讲到这里就差不多了。现在我们已经拥有了一个升级版的寄存器分配算法。采用这个算法生成的汇编文件,看上去就很顺眼了,你会看到大部分指令的操作数都是寄存器了。
|
||
|
||
那么,现在又到了检验我们的成果的时候了。是不是现在这个版本的性能会提升很多呢?毕竟,在之前的版本中,我们在使用本地变量和参数的时候,都要访问内存。而且根据我们前面的经验,内存会比寄存器慢差不多100倍呀。
|
||
|
||
## 再次进行性能比拼
|
||
|
||
与其在这猜测,不如直接动手验证吧。
|
||
|
||
你可以运行make example\_fibo命令,再来构建一次斐波那契数列的例子,然后用./example\_fibo命令来执行它。并且,你还可以用make fibo命令来编译一遍fibo.c,也就是C语言版本的斐波那契数列程序。
|
||
|
||
在这节课的Makefile文件中,我给fibo命令添加了-O2编译选项,也就是生成的代码是优化过的,也会使用寄存器。
|
||
|
||
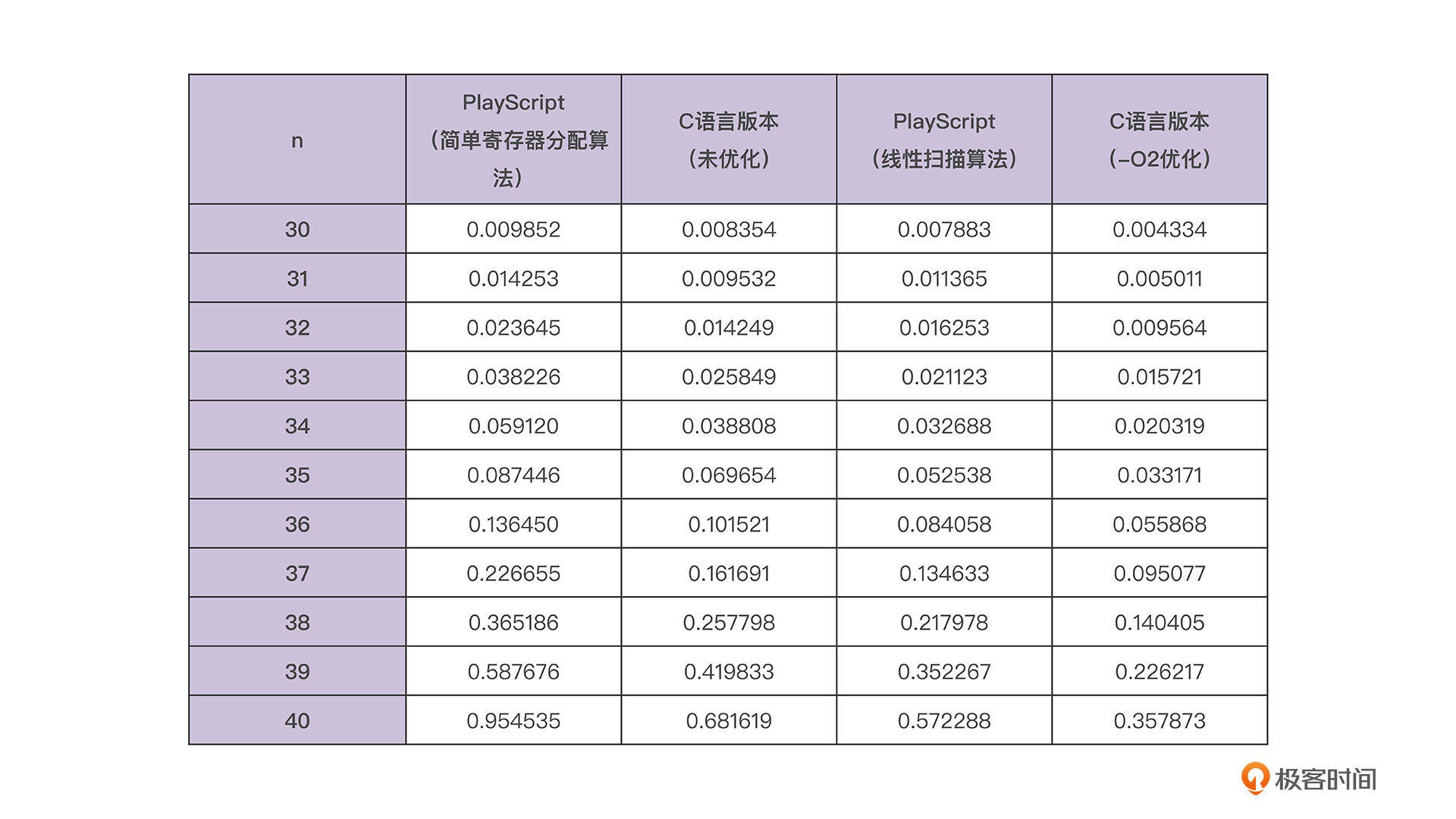
我再一次把计算结果贴上来,你可以看看下面的表格。不过这里你要注意一下,在表格里,我把当前实现的这个TypeScript的版本叫做PlayScript,称呼起来更加方便一些。这是我比较喜欢的一个名称,我在[《编译原理之美》](https://time.geekbang.org/column/intro/100034101)课程中就用过这个名称。
|
||
|
||
|
||
|
||
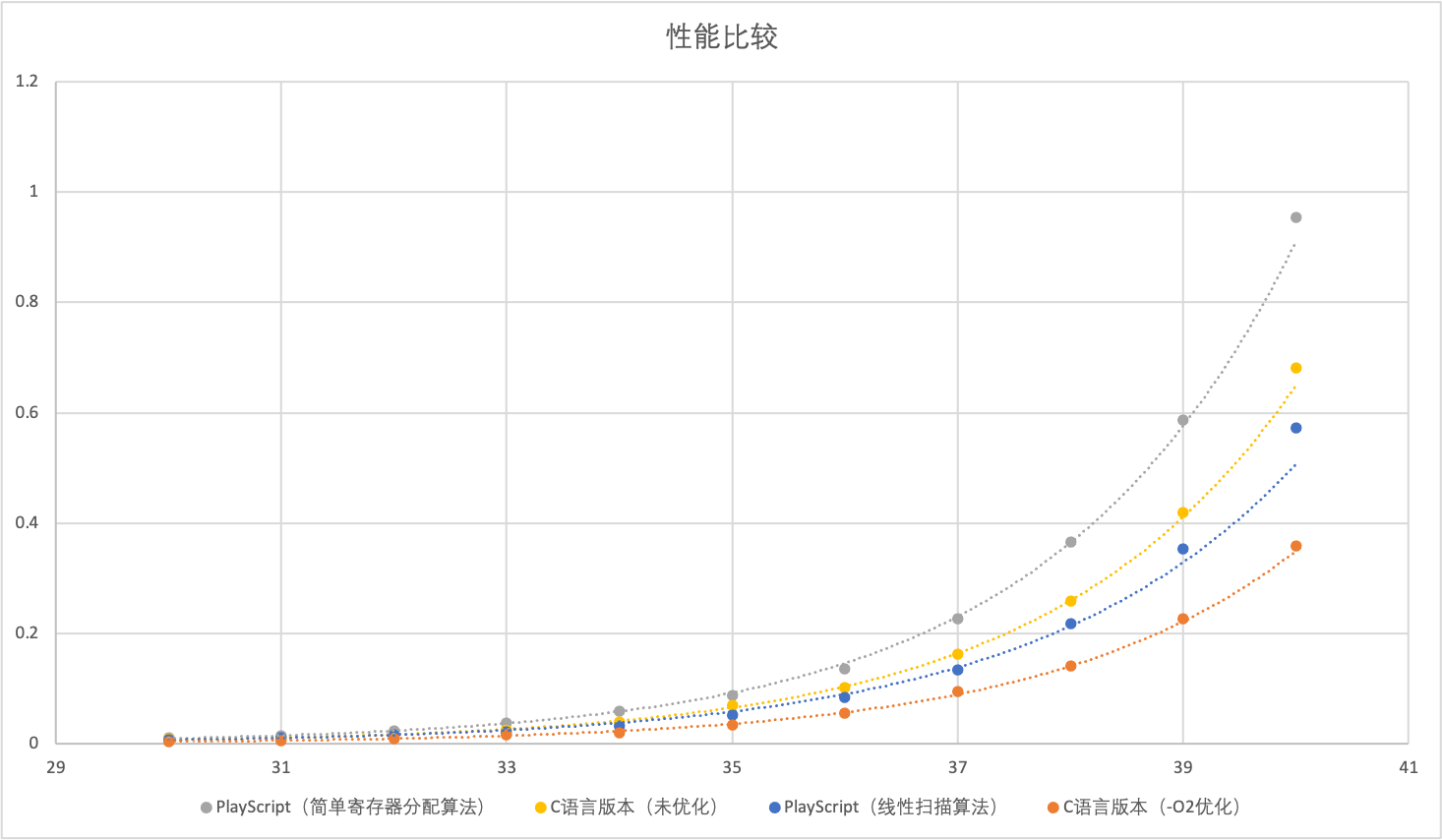
而且,我仍然做了一张曲线图,让你能够更直观地看到各个版本之间的差别。
|
||
|
||
|
||
|
||
从这些数据和图表中,你能得到什么结论呢?你可以停一两分钟,自己先想一下。
|
||
|
||
首先,采用了线性扫描算法以后,我们程序的性能果然有提升(图中的蓝线),超过了采用简单寄存器算法的版本,也超过未优化的C语言版本。
|
||
|
||
不过,你有没有觉得有点不对劲?哪里不对劲呢?**看上去,这性能的提升也没有特别大呀,还不到1倍**。在我内心中,其实期待着更大的性能提升。毕竟我们说过,内存读写的速度可比寄存器的速度慢上百倍呢。
|
||
|
||
那么,是什么原因导致了这个结果?你可以想一下。其实,你想想我们前面介绍过的关于CPU的架构的知识就知道了。导致这个结果的原因,其实是**CPU的高速缓存**。
|
||
|
||
在程序运行期间,我们栈桢里的那点数据,都被放到高速缓存去了,导致读写速度要比内存快得多。这个例子也从侧面反映出了,保证数据的局部性有多么重要。
|
||
|
||
那是不是我们费这么大劲升级的寄存器分配算法其实没啥用呢?
|
||
|
||
也不是的。在我测试的时候,我的电脑只运行了这一个比较占用CPU的程序。而如果你写的是一个服务器程序,有大量并发访问,每个并发访问都要访问内存中不同地方的数据,那么CPU的高速缓存的内容就要不断地刷新,它对内存访问的增速作用就会大打折扣。
|
||
|
||
这个时候,采用优化的寄存器分配算法的程序,在性能上一定会有碾压。如果你有兴趣,可以搭建一个这样的测试环境测一下,看看实际的性能差别到底会多大。
|
||
|
||
好了,这是我从数据中看到的第一个疑问,以及对这个疑问的分析。
|
||
|
||
**然后呢,还有第二个疑问:用-O2参数优化了的C语言的版本,还是比PlayScript的优化版快,快了大约50%,这又是什么原因导致的呢?**按理说,这两个版本都是用寄存器来作为操作数的,性能差异应该不大才对呀。
|
||
|
||
你可以比较一下[example\_fibo.s](https://gitee.com/richard-gong/craft-a-language/blob/master/20/example_fibo.s)和[fibo.s](https://gitee.com/richard-gong/craft-a-language/blob/master/20/fibo.s)这两个汇编代码的差别。你现在看这些汇编代码应该越来越亲切了吧?
|
||
|
||
你看,虽然实现的都是相同的功能,但我们生成的汇编代码,确实跟C语言(也就是llvm)生成的不一样,区别有几个方面。
|
||
|
||
首先是使用的具体寄存器不一样,但这个其实对性能没有什么影响。
|
||
|
||
第二方面的差别呢,是使用的某些指令不同。比如我们做减法的时候用的是subl指令,而fibo.s中用的是leal指令。leal指令能用一条指令完成计算和给另一个寄存器赋值的动作,所以性能确实更高一点。
|
||
|
||
但这也不是导致50%那么多的性能差异的原因啊。如果你不信,你可以把example\_fibo.s中的subl和movl两条指令用leal指令来替换一下,然后再编译一下看看,性能其实没有太大区别。
|
||
|
||
那这个主要的原因到底在哪呢?你如果再仔细看fibo.s,你会发现其实它是在**运行逻辑**上做了比较大的优化。
|
||
|
||
比如,斐波那契数列的公式是:f(n) = f(n-1) + f(n-2)。
|
||
|
||
把f(n-2)展开后,又得到:f(n) = f(n-1)+f(n-3)+f(n-4)。
|
||
|
||
像这样把最后一项持续展开,又得到:f(n) = f(n-1) + f(n-3) + f(n-5) + … + f(2)或f(1)。
|
||
|
||
你会注意到,采用上面这样的算法,fibo.s中的递归调用变成了循环调用,每个循环要把n的值减少2。
|
||
|
||
把递归转化为循环,其实是编译技术中常见的一个技术,它能有效地减少总的函数调用次数,从而减少每次函数调用由于建立新栈桢、保护寄存器等引起的开销,看来这就是我们性能不如人的主要原因了。
|
||
|
||
当然了,我们目前对优化技术的接触还不太多。其实我们这两节课学习到的寄存器分配算法,算是后端优化技术的一种,其他优化技术其实还很多。
|
||
|
||
看来,我们仍然有不少知识点需要探索呀!不过也没关系,就把这些挑战当成我们进一步学习的动力吧!
|
||
|
||
## 课程小结
|
||
|
||
今天这节课我们就讲到这里了,通过这节课,我希望你记住这几个知识点:
|
||
|
||
首先,在变量活跃性分析的具体实现上,我们需要能够知道每个变量是在什么时候定义的、什么使用使用的。在我们原来的LIR中,能够获取变量使用的信息,但缺少变量定义的信息。所以我增加了一个伪指令,用来弥补这个缺陷。
|
||
|
||
第二,在存在多个基本块的情况下,我们要首先计算出CFG,然后采用基于图的算法来计算每个基本块的变量活跃性集合。这个计算过程可能要迭代多次,直到所有基本块的变量活跃性集合不再变化为止。
|
||
|
||
第三,在具体实现线性扫描算法时,其中的重点就是根据变量的活跃性寻找可用的寄存器。如果寄存器数量不足,我们就要选择一个变量溢出到内存中。而且在调用函数时,也是通过溢出到内存的方法,来保存Caller需要保护的寄存器。最后,我们要计算清楚每个溢出的变量的准确内存地址和所占空间,从而正确的维护栈桢。
|
||
|
||
## 思考题
|
||
|
||
你能否研究一下PlayScript当前生成的汇编代码,看看它还有哪些地方可以进一步优化的?优化的思路是什么呢?欢迎在留言区分享你的观点。
|
||
|
||
欢迎你把这节课分享给更多感兴趣的朋友。我是宫文学,我们下节课见。
|
||
|
||
## 资源链接
|
||
|
||
[这节课的示例代码在这里!](https://gitee.com/richard-gong/craft-a-language/tree/master/20)
|
||
|