12 KiB
25 | 动态规划(下):背包问题与动态规划算法优化
你好,我是胡光,欢迎回来。
上节课呢,我们学习了动态规划算法的一般求解步骤:状态定义,推导状态转移方程、正确性证明,以及程序设计与实现。在这个过程中,我们又一次用到了之前我们讲的重要数学思维:数学归纳法 。
今天这节课,将是我们“算法数据结构篇”的最后一篇,其实从这个章节开始,我都在试图用我的语言和有序的课程设计,让你感受算法数据结构在思维层面的魅力。我还希望,你能通过这部分知识的学习,能对算法和数据结构产生兴趣,并且消除对算法学习的畏难心理。
好了,进入正题,今天我将借由动态规划算法,向你展示算法中追求极致的那一部分基因:算法优化。
初识:0/1 背包问题
想要感受算法优化,我们先从一类经典的动态规划问题,背包类问题开始。
简单的背包类问题,可以分成三类:0/1背包问题,完全背包问题与多重背包问题。我们今天要讲的就是 0/1背包与多重背包这两个问题。
0/1背包问题可以说是所有背包问题的基础,它描述的场景是这样的:假设你有一个背包,载重上限是 W,你面前有 n 个物品,第 i 个物品的重量是 wi,价值是 vi,那么,在不超过背包重量上限的前提下,你能获得的最大物品价值总和是多少?
按照动态规划问题的四步走,咱们来分析一下这个问题。
1. 状态定义
关于状态定义,我们首先来分析0/1背包问题中的自变量和因变量。
因变量比较好确定,就是问题中所求的最大价值总和。自变量呢?经过分析你会发现,物品种类和背包承重上限就是自变量,因为它们都能够影响价值总和的最大值。这样我们就可以设置一个二维的状态,状态定义如下:
0/1背包状态定义:dp[i][j] 代表使用前 i 个物品,背包最大载重为 j 的情况下的最大价值总和。
2. 推导状态转移方程
推导状态转移方程,也就是推导 dp[i][j] 的表达式。根据 dp[i][j] 的含义,我们可以将 dp[i][j] 可能达到最大值时的方案分成两类:一类是方案中不选择第 i 个物品的最大价值和,另一类是方案中选择了第 i 个物品的最大价值和。只需要在这两类方案的最大值中,选择一个价值和较大的方案,转移到 dp[i][j] 即可。下面,我们就分别表示一下这两种方案的公式。
不选择第 i 个物品的最大价值和,就是 dp[i - 1][j]。也就是说,在背包最大载重为 j 的情况下,前 i 个物品中,不选择第 i 个物品的最大价值和,就等于在前 i - 1 个物品中选择的最大价值和。
选择第 i 个物品的最大价值和就是 dp[i - 1][j - wi] + vi。关于这个公式的理解,可以参考我们前面讲的凑钱币问题,既然要求一定选择了第 i 个物品,那我们就可以先给第 i 个物品预留出来一个位置,然后给剩余的 i - 1 个物品留的载重空间就只剩下 j - wi 了,那么 i - 1 个物品选择的最大价值和是 dp[i - 1][j - wi],再加上 vi 就是选择第 i 个物品时,我们能够获得最大价值和。
最终,我们得到 dp[i][j] 的状态转移方程,如下所示:
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - w[i]] + v[i])
3. 正确性证明
动规算法的正确性证明,还是需要依赖于数学归纳法,下面我们开始数学归纳法的三步走。
首先,dp[0][j] = 0,就是当没有物品的时候,无论背包限重是多少,能得到的最大价值和都是0,这也就是已知 k0 正确。
其次,假设我们已经正确计算得到了,在 i - 1 个物品的任意一种背包容量下的价值最大和值,也就是所有 dp[i - 1] 中的值。那么根据状态转移方程,我们也肯定可以正确的得到所有 dp[i] 中的值。
最后两步联立,整个求解过程对于任意 dp[i][j],均正确。
请你认真理解这个证明过程,因为接下来的程序处理过程,其实和这个证明过程是一致的。
4. 程序设计与实现
完成了关于0/1背包问题的求解过程后,最后我们来看看程序的设计与实现。下面呢,是我给出的一段参考代码:
#define MAX_N 100
#define MAX_V 10000
int v[MAX_N + 5], w[MAX_N + 5];
int dp[MAX_N + 5][MAX_V + 5];
int get_dp(int n, int W) {
// 初始化 dp[0] 阶段
for (int i = 0; i <= W; i++) dp[0][i] = 0;
// 假设 dp[i - 1] 成立,计算得到 dp[i]
// 状态转移过程,i 代表物品,j 代表背包限重
for (int i = 1; i <= n; i++) {
for (int j = 0; j <= W; j++) {
// 不选择第 i 种物品时的最大值
dp[i][j] = dp[i - 1][j];
// 与选择第 i 种物品的最大值作比较,并更新
if (j >= w[i] && dp[i][j] < dp[i - 1][j - w[i]] + v[i]) {
dp[i][j] = dp[i - 1][j - w[i]] + v[i];
}
}
}
return dp[n][W];
}
可以看到,get_dp 函数就是求解0/1背包问题的过程,函数传入两个整形参数 n 和 W,分别代表了物品数量与背包最大限重。程序中有三个数组:v、w 与 dp,v[i] 代表第 i 个物品的价值,w[i]代表第 i 个物品的重量,dp[i][j] 代表背包问题相关的状态。
这一段代码,采用了正向递推的程序实现。而且,如果你注意观察 get_dp 函数的实现过程,你会惊奇地发现,这就是数学归纳法的证明过程。
首先,初始化 dp[0] 阶段的所有值,也就是保证了 k0 成立;然后从 dp[1] 开始迭代计算到 dp[n] 中所有值,每一次 dp[i]依赖的就是 dp[i - 1] 中的值,只有 dp[i - 1] 中所有值是正确的,才能保证 dp[i]中所有值是正确的,这就是数学归纳法的第二步。最后,两步联立,就证明了以 dp 数组的第一维作为阶段,进行状态转移,计算得到的所有 dp 值均是正确的。
面对这种更加广义的数学归纳法,我们也有一个名称,叫做“结构归纳法”。
进阶:多重背包问题
接下来我们提高一下问题的复杂度,说说多重背包问题。
其实这个问题,整体和0/1背包问题类似,只不过从 n 个物品变成了 n 种物品,且每种物品都有不同的数量,我们可以设定第 i 种物品的数量是 ci。
现在你有一个载重上限为 15kg 的背包,有如下 4 件物品:
- 镀金极客币,每个4kg,每个价值 10 块钱,一共有 5 个;
- 胡船长手办,每个3kg ,每个价值 7 块钱,一共有 4 个;
- 西瓜,每个12kg ,每个价值 12 块钱,一共有 2 个;
- 哈密瓜,每个9kg ,每个价值 8 块钱,一共有 7 个。
经过分析,在不超过背包载重上限的情况下,你可以选择3个镀金极客币和1个胡船长手办装到背包里面,这种选择方案能获得最大价值为:37 块钱。
回到我们说的这个多重背包问题,你想如何求解呢?
其实最简单的解决办法,就是把 n 种物品中的每一个,都看成是0/1背包中的一个物品,然后按照 0/1背包问题的求解过程来做即可。这也就是说,如果一种物品有 12 件,就相当于0/1背包中多了 12 件物品,我们就多做 12 轮运算,要是有 120 件呢,那就是多做 120 轮运算。
这种做法虽然可行,可显然太浪费我们计算机的计算资源了。下面就让我们看看怎么做,才能更优化。
1. 二进制拆分法
我们先来想象另外一个场景,假设你是一个卖白菜的老农,手上有23斤白菜和若干个筐,出于某种不知名的原因,你今天不能把称重器带到菜市场,只能提前把白菜称好装入不同的筐里贩卖给顾客。问题来了,白菜要如何分到这些筐里面,才能使得第一个顾客无论要多少斤白菜,你都能通过挑选其中的几筐白菜,从而满足顾客的需求呢?
一种最直接的装筐方法,就是每个筐里面装 1 斤白菜,共需要23个筐。这样,第一个顾客要多少斤白菜,你就给他多少筐就行。这种方法简单粗暴,可是用的筐太多了。
我们转换一个思路去想这件事:当你准备挑几个筐满足第一个顾客需求的时候,对于每个筐来说,都有两种状态,选或者不选,这不就是二进制每位上的数字么?我们就可以把每个筐,看成是二进制相应的位权。
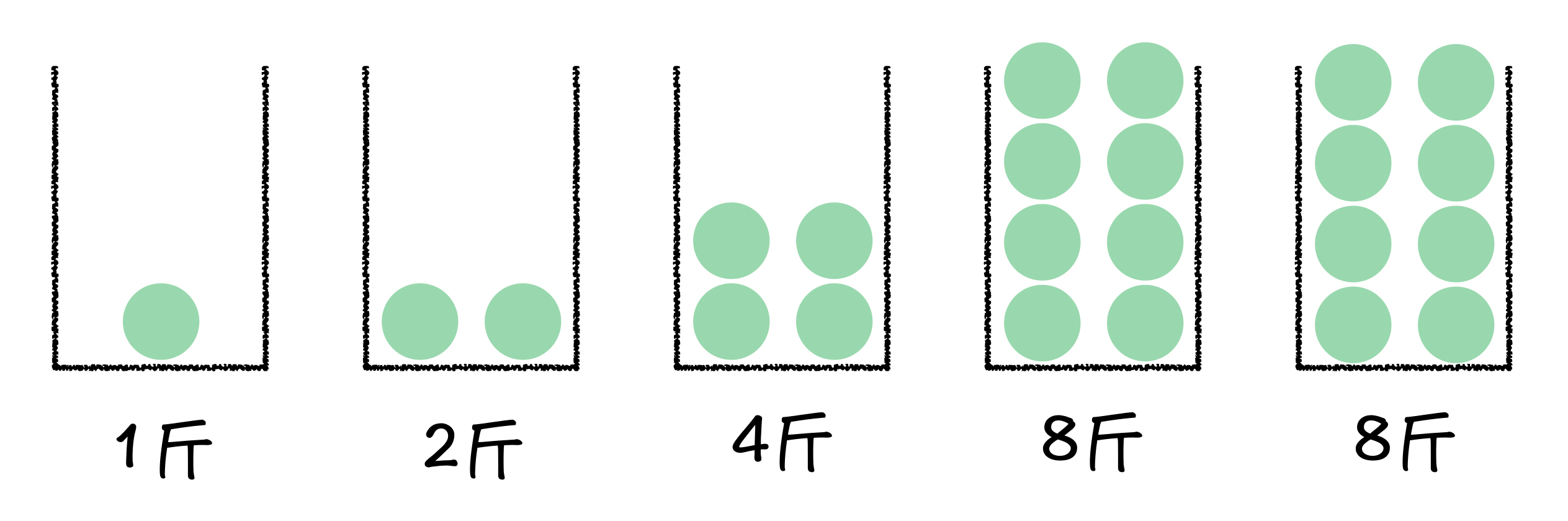
可以看到,从第一个筐开始,我们依次装上 1 斤、2 斤、4斤、8 斤,第五个筐应该装16斤的,可剩下的白菜不够 16 斤,所以就一起放到最后一个筐里面。这样,我们只需要 5 个筐,就装了 23 斤白菜,并且可以保证无论第一个客人要几斤白菜,都能满足他的需求。
以上,就是我讲的二进制拆分法。
2. 多重背包的拆分优化
看完二进制拆分法以后,我们再看看多重背包转0/1背包的这种解题思路有什么问题。
假设多重背包中,某一种物品有 23 件,转换到0/1背包问题中,就是 23 个物品,就跟前面一斤白菜装一筐的做法是一样的。我们虽然不知道,在0/1背包问题的最优方案中,这种物品被具体选择了多少件,可是只要我们通过一种合理的拆分方法,使得无论最优方案中选择了多少件这种商品,我们都可以组合出来。
简单粗暴地拆分成 23 份,是一种拆分方法,而二进制拆分法也是一种拆分方法,并且二进制拆分法只需要拆成 5 份物品,作为0/1背包问题中的 5 个单独的物品即可,这么做可以达到和拆分成 23 件物品等价的效果,并且节省了大量的计算资源。
例如,前面多重背包问题的那个例子中,按照原本简单粗暴的方式,我们是把 5 个镀金极客币、4 个胡船长手办、2 个西瓜、7 个哈密瓜,当作 18 个物品的0/1背包问题来求解的。但如果采用二进制拆分法,我们就会得到如下拆分方案:
1个镀金极客币,4kg每个,价值 10 块钱
2个镀金极客币,8kg每个,价值 20 块钱
2个镀金极客币,8kg每个,价值 20 块钱
1个胡船长手办,3kg每个,价值 7 块钱
2个胡船长手办,6kg每个,价值 14 块钱
1个胡船长手办,3kg每个,价值 7 块钱
1个西瓜,12kg每个,价值 12 块钱
1个西瓜,12kg每个,价值 12 块钱
1个哈密瓜,9kg每个,价值 8 块钱
2个哈密瓜,18kg每个,价值 16 块钱
4个哈密瓜,36kg每个,价值 32
这种拆分方案等价于求解 11 个物品的0/1背包问题,比之前求解的18个物品的 0/1背包问题显然要优秀。
实际上,随着某个物品数量的增加,二进制拆分法的优势会愈加地明显。想一想 32 个二进制位能表示的数字大小,你就明白了。
3. 程序设计与实现
关于多重背包优化版本的程序,给你留作一个作业题,请你根据本节所讲的内容,用二进制拆分法实现多重背包的优化程序。相信你没问题的!
课程小结
按照惯例,最后我来做一下这节课的知识点总结:
- 0/1背包问题中的自变量是物品的种类和背包限重,所以我们把这两维设计到了状态定义中。
- 多重背包问题可以转换成 0/1背包进行求解,转换过程不同,效率也就不同。
- 二进制拆分法,本质思想就是二进制的数字表示法,0/1 表示两种状态,表示选或不选。
好了,“算法数据结构篇”到这里就结束了,日后若有机会,我希望跟你分享更多编程中的美妙思维过程。
我是胡光,我们最后一章见。