14 KiB
14 | 框架思维(上):将素数筛算法写成框架算法
你好,我是胡光,咱们又见面了。
上一节呢,我们提到了一个词,叫做“算法思维”,就是用算法去解决问题的思维方式,并且说明了算法思维有别于我们通常所说的“算法”。那么如何锻炼算法思维呢?
今天我要说的这个方法,就叫做“照猫画虎”。什么意思呢?如果我们把一个个具体的算法称之为猫,而每个具体算法中所能锻炼的“算法思维”就是那只虎。也就是说,我们可以通过学习一些简单具体的算法,来总结一些重要的算法思维。
接下来的两节中,我先带你锻炼的是算法思维中的“框架思维”,所谓框架思维就是将一个具体的算法学成一个框架,变成一个可以解决多个问题的利器。废话不多说,开始今天的课程吧。
今日任务
在开始今天的学习之前,先让我们来看看今天这 10 分钟的任务吧。这个任务很简单,就是求 1 万以内所有素数的和。
素数,也叫做质数,就是只能被 1 和其本身整除的数字。举例说,30 以内的素数依次是:2、3、5、7、11、13、17、19、23、29,这几个数字相加之和,等于 129。
而与素数相对的概念,就是合数,它指的是除了能被1和其本身整除以外,还可以被其他数字整除的数字。你可以简单理解为合数是由若干个素数相乘得到的数字,也就是说一个合数,一定能被某个素数整除。例如,6 就是合数,能被 2 和 3 这两个素数整除。
这里我多说几句,素数在数论当中(关于什么是数论,感兴趣的同学可以自行搜索了解),是一个很重要的概念,而数论可以说直接奠定了我们当代互联网经济的基础,那就是“信息安全”。试想,如果不能保证信息安全,你敢在网上使用你的手机号,进行某些登录操作么?如果不能保证信息安全,你敢在网络上购物,支付买单么?如果信息不安全,你敢和你的朋友在聊天工具上畅所欲言么?这一切的一切,都与我们今天说的素数有关系,你说素数重不重要?下面让我们正式开始今天的学习吧。
必知必会,查缺补漏
今天我将给你介绍一个算法,就是素数筛算法。这个算法呢,思想很直接,也很简单,相信我,你肯定可以学会的。
1. 素数筛算法介绍
所谓素数筛,是将其产出的信息存储在一个标记数组中,数组的第 i 位,标记的是 i 这个数字是否是合数的信息。如果 i 这个数字是合数,数组下标为 i 的位置就被标记成为 1,如果 i 不是合数,则数组下标为 i 的位置就是 0。素数筛就是通过一套算法流程,产生一个这样的数组。
可以看到,素数筛的作用就是把所有合数标记出来,在知道了这个范围内所有的合数之后,也就很容易找出这个范围内所有的素数了。
沿着这个思路,算法中要解决的第一个问题,就是如何标记合数?这个就要回忆一下合数的特征了,根据前面的解释,我们知道一个合数一定能被某个素数整除,也就是一定是某个素数的整数倍。也就是说,如果 2 是素数,那么 2 的 2 倍、3 倍、4 倍等等,一定不是素数,我们就可以把 4、6、8 这些数字分别标记为合数。
这个做法里面,你会发现好像有一个死结,我们要标记掉所有合数,就需要找到所有素数,这就又回到最开始素数筛要解决的问题,这不就变成了一个先有鸡,还是先有蛋的问题了么?其实不然,下图是我整理的算法流程:
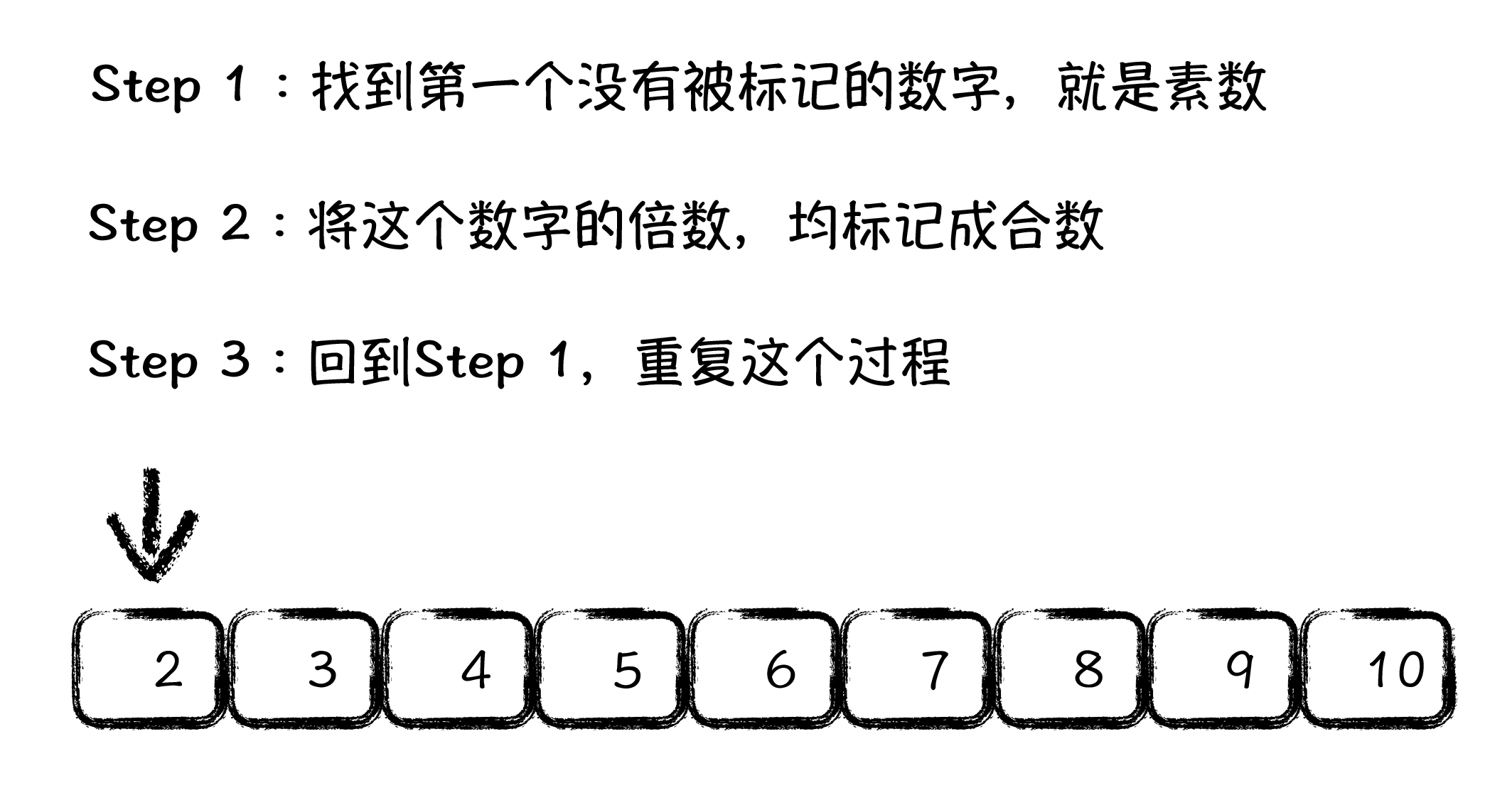
素数筛算法从 2 开始,执行若干轮,每一轮呢,找到第一个没有被标记掉的数字,可以猜想到,这个数字就一定是素数。为什么呢?其实用我们之前说的“数学归纳法”就可以证明。
首先,2 是第一个没有被标记的数字,所以 2 肯定是素数,然后我们可以正确的标记掉所有 2 的倍数。假设在数字 n 之前,我们正确找到了所有素数,并且将这些素数的倍数均标记掉了,那么 n 作为后续第一个没有被标记掉的数字,n 就一定素数,最后,我们可以用 n 标记掉 n 所有的倍数,这也就保证了后续过程的正确性。在这个过程中,其实也证明了整个素数筛算法的正确性。
为了让你有个更直观的感受,我给你整理了10以内,素数筛算法前三轮的示意图:
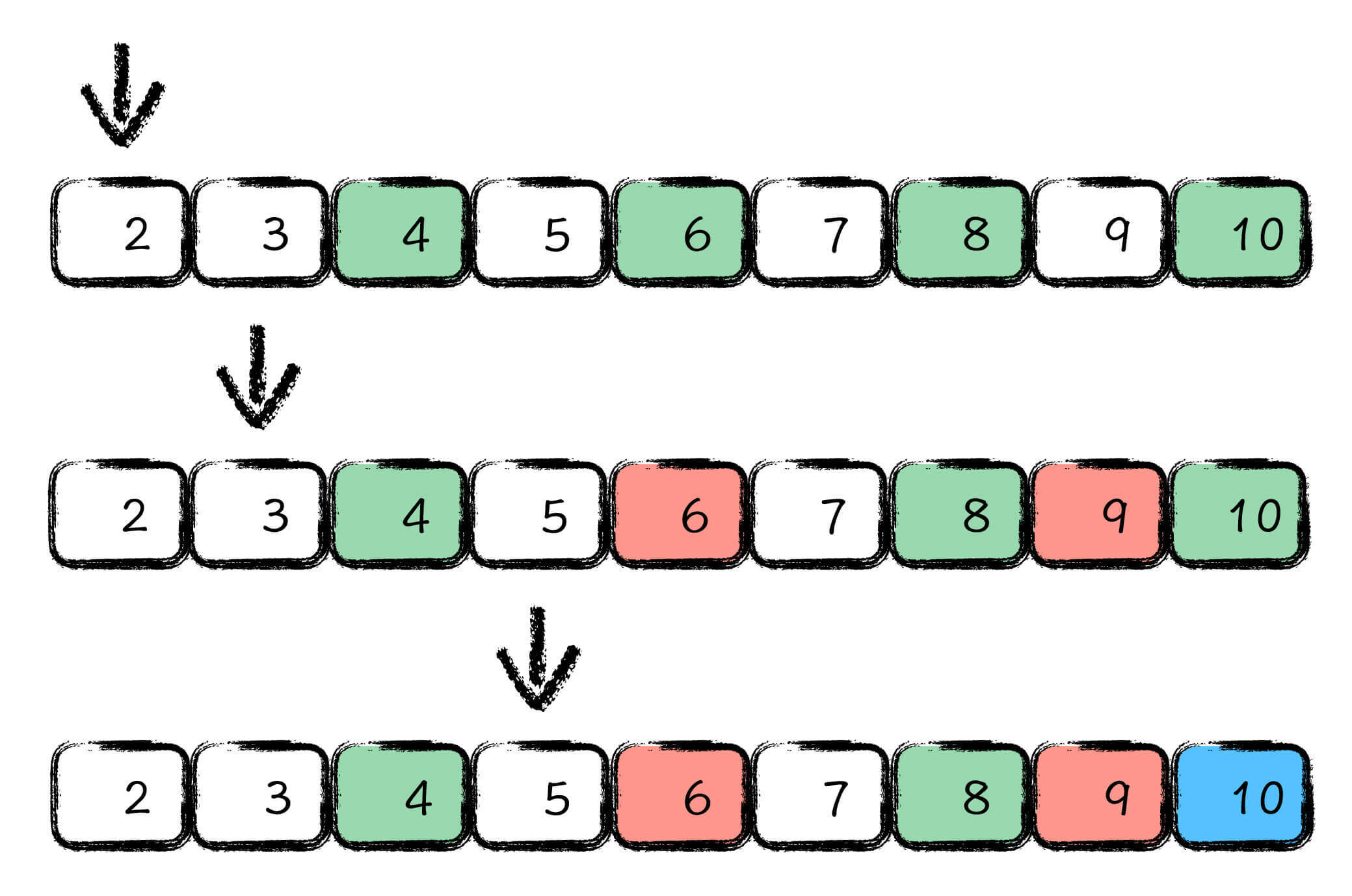
如图所示,第一轮的时候,2没有被标记掉,我们就使用2 标记掉所有2的倍数,标记掉的就是 4、6、8、10 这四个数字;第二轮的时候,继续向后找,第一个没有被标记掉的数字是 3,那么我们接着标记掉范围内所有 3 的倍数,就是 6、9 这两个;第三轮,发现 5 没有标记掉,那么就用 5 去标记了 10 这个数字。
2. 素数筛代码框架总结
在认识了基本的素数筛算法以后,让我们看看素数筛的具体代码实现,下面的示例代码呢,演示了如何标记 10000 以内所有合数,以此来找到这个范围内所有的素数。
int prime[10005] = {0};
void init_prime() {
// 素数筛的标记过程
for (int i = 2; i * i <= 10000; i++) {
if (prime[i]) continue;
// 用 j 枚举所有素数 i 的倍数
for (int j = 2 * i; j <= 10000; j += i) {
prime[j] = 1; // 将 j 标记为合数
}
}
return ;
}
如代码所示,init_prime 就是素数筛算法的过程,并把最终生成的信息都存储在了 prime 数组中,如果prime[i] 为 1 ,说明 i 是合数。
这个算法流程中呢,包含了两层循环结构,外层循环结构,从 2 开始遍历到根号 10000,也就是 100。其中这里还用到了一个编程技巧,原本代码应该写成:i <= sqrt(10000) 的这个不等式,而加上了左右平方,就变成了上面的 i * i <= 10000 这样的代码。这种改变是有好处的,会在代码运行速度上做提升,毕竟开方运算是很慢的,远远没有单独做一个乘法操作要快。
第 5 行代码,是判断 i 这个数字是否被标记过的,如果被标记过,就说明是合数,就不执行后续操作。当代码到了第6行的时候,说明此时 i 这个数字,一定是素数,我们就用内部的 j 循环,遍历所有数字 i 的倍数,并且将 prime[j] 标记为 1,也就是将 j 这个数字标记为合数。
执行完 init_prime 函数以后,prime 数组中就是所有合数的标记信息,反向思维就能找到所有素数,就是那些没有被标记掉的数字。
在这份代码中,你需要注意以下两点:一是到了代码的第 6 行,数字 i 有什么特性?二是为什么外层循环 i 只需要遍历到根号 10000 即可?
第一点比较好理解,到了代码第6行,这时候访问到的 i 一定是素数。第二点呢,就要从合数的特点思考了,合数一定可以表示为两个非 1 整数的乘积形式,否则那就是素数了。例如,6可以拆解成 2 * 3,39 可以拆解成 3 * 13 等等。而质数 7 呢,只能表示成 1 * 7,这不是两个非 1 整数。
而用来表示合数 n 的这两个数字,一定是一个小于等于根号 n,一个大于等于根号 n。我们再具体看那个小于等于根号 n 的数字,假设它是数字a ,如果a是素数,那么在素数筛算法中,i 遍历到根号 n,数字 a 一定可以正确的标记掉数字 n;而如果数字a不是素数,而是一个合数,那说明数字 n 可以被一个更小的数字标记掉。这也就说明,外层循环 i 只需要遍历到根号 n,就可以正确的标记掉 n 这个范围内所有的合数。
在你学习这份代码的时候,或者以后自学某些其他算法代码的时候,清晰地知道这份代码到了第几行,某些变量的取值有什么性质,这是理解框架性思维的最重要的一步。只有这样,你才能游刃有余地使用你所会的所有的算法代码。
最后,我们来说一下素数筛这个代码中最重要的性质吧,其实就是前面提到的“当代码到了第 6 行的时候,i 一定是素数”。这是你理解算法代码的第一步,所以我也不打算给你灌输太多内容,就这一点就够了,在后续的学习中,你会看到这一点所能扩展出来的其他代码形式。
一起动手,搞事情
思考题:因子分解程序正确性证明
今天的思考题呢,和整数的素因子分解有关。所谓的素因子分解,就是把一个整数,表示成为若干个素数相乘的形式,并且我们可以轻松的证明,这种只由素数表示的分解表示法,对于某个特定整数 N 来说,一定是唯一的。例如,67689 这个数字就可以分解为:3 * 3 * 3 * 23 * 109 = 67689,其中3、23、109 都是素数。
下面呢,我给你准备了一段素因子分解的程序:
#include <stdio.h>
// 打印一个素因子,并且在中间输出 * 乘号
void print_num(int num, int *flag) {
if (*flag == 1) printf(" * ");
printf("%d", num);
*flag = 1;
return ;
}
int main() {
int n, i = 2, flag = 0, raw_n;
scanf("%d", &n);
raw_n = n;
// 循环终止条件,循环到 n 的平方根结束
while (i * i <= n) {
//①:只要 n 可以被 i 整除,就认为 i 是 n 的一个素因子
while (n % i == 0) {
print_num(i, &flag);
n /= i;
}
i += 1;
}
//②:如果最后 n 不等于 1,就说明 n 是最后一个素数
if (n != 1) print_num(n, &flag);
printf(" = %d\n", raw_n);
return 0;
}
今天的任务呢,就是请你解释 ① 处和 ② 处所写注释的正确性,也就是证明:
- 第 18 行代码中,只要 n 可以被 i 整除,i 就一定是素数,为什么?
- 第 25 行代码中,为什么只要 n 不等于1,n 就一定是素数呢?
由于程序中用了循环,那么循环程序正确性的证明,你还记得吧?需要用到“数学归纳法”。而今天这两个程序过程中具体的证明,我可以给你一个小提示,尝试用“反证法”证明一下。
计算素数和
准备完了前面这些基础知识以后,最后让我们回到今天的任务:求出 1 万以内所有素数的和。如果你掌握了素数打表相关的算法以后,就很容易整理出解题思路,那就是利用素数打表算法标记掉 1 万以内所有的合数,然后将剩余的所有未被标记的数字相加,即可得到我们想要的结果。代码也不难,如下所示:
#include <stdio.h>
#define MAX_N 10000
int prime[MAX_N + 5];
// 初始化素数表
void init_prime() {
prime[0] = prime[1] = 1;
for (int i = 2; i * i <= MAX_N; i++) {
if (prime[i]) continue;
for (int j = 2 * i; j <= MAX_N; j += i) {
prime[j] = 1; // 将 j 标记为合数
}
}
return ;
}
int main() {
init_prime();
int sum = 0;
for (int i = 2; i <= MAX_N; i++) {
sum += i * (1 - prime[i]); // 素数累加
}
printf("%d\n", sum);
return 0;
}
如上这段程序中,首先调用 init_prime 过程初始化 prime 数组。正如你看到的,init_prime 中,用到的是素数筛法,你可以自行改写成欧拉筛法,关于欧拉筛法,你可以自行查阅相关资料,如果经过你修改的程序,输出结果没有变,说明你的实现是没有问题的。
然后在主程序中,依次将每个素数累加到 sum 变量中,这里用到了一个我们之前讲过的技巧,就是用 1 - prime[i] 计算的结果,充当条件选择器:结果为 1 的时候,说明 i 为素数,就会往 sum 中累加一个 i * 1 ,也就是 i;如果结果为 0,说明 i 不是素数,就会往 sum 中累加一个 i * 0,也就是 0。最后,就是把所有素数全部累加到了 sum 变量中。
其实这段代码中,我最想讲的,是那个 MAX_N 宏的定义与使用。你会发现,程序中有三处用到了 MAX_N 宏,试想一下,如果我们现在想要修改程序的求解范围,修改成求解 100 万以内的所有素数累加之和,如果没有 MAX_N 宏的话,程序中我们最少要修改三个地方。
为什么说是最少修改三个地方呢?因为100万以内素数的和,很有可能超过 int 的表示范围,所以可能连 sum 的类型也要改掉。而使用了 MAX_N 宏这个技巧以后呢,我们只需要修改代码的一个地方,就可以确保,程序中所有和范围相关的地方,都被修改掉了。
课程小结
最后我们来做一下今天的课程总结,我希望你记住如下三点:
- 想把具体“算法”升华成“算法思维”,首先要习惯性地总结算法的“框架思维”。
- 素数筛是用素数去标记掉这个素数所有的倍数。
- 清楚地知道素数筛在执行过程中,每一行的性质。
这里,我希望你一定要熟记素数筛的算法框架,下一节我们将使用素数筛这个框架,解决几个其他问题,让你好好体会一下算法代码的“框架思维”。
好了,今天就到这里了,我是胡光,我们下期见。