414 lines
19 KiB
Markdown
414 lines
19 KiB
Markdown
|
|
# 15 | 如何用极坐标系绘制有趣图案?
|
|||
|
|
|
|||
|
|
你好,我是月影。
|
|||
|
|
|
|||
|
|
在前面的课程中,我们一直是使用直角坐标系来绘图的。但在图形学中,除了直角坐标系之外,还有一种比较常用的坐标系就是极坐标系。
|
|||
|
|
|
|||
|
|
[](http://zh.wikipedia.org)
|
|||
|
|
|
|||
|
|
你对极坐标系应该也不陌生,它是一个二维坐标系。与二维直角坐标系使用x、y分量表示坐标不同,极坐标系使用相对极点的距离,以及与x轴正向的夹角来表示点的坐标,如(3,60°)。
|
|||
|
|
|
|||
|
|
在图形学中,极坐标的应用比较广泛,它不仅可以简化一些曲线方程,甚至有些曲线只能用极坐标来表示。不过,虽然用极坐标可以简化许多曲线方程,但最终渲染的时候,我们还是需要转换成图形系统默认支持的直角坐标才可以进行绘制。在这种情况下,我们就必须要知道直角坐标和极坐标是怎么相互转换的。两个坐标系具体转换比较简单,我们可以用两个简单的函数,toPolar和fromPolar来实现,函数代码如下:
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
// 直角坐标影射为极坐标
|
|||
|
|
function toPolar(x, y) {
|
|||
|
|
const r = Math.hypot(x, y);
|
|||
|
|
const θ= Math.atan2(y, x);
|
|||
|
|
return [r, θ];
|
|||
|
|
}
|
|||
|
|
|
|||
|
|
// 极坐标映射为直角坐标
|
|||
|
|
function fromPolar(r, θ) {
|
|||
|
|
const x = r * cos(θ);
|
|||
|
|
const y = r * sin(θ);
|
|||
|
|
return [x, y];
|
|||
|
|
}
|
|||
|
|
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
那今天,我们就通过参数方程结合极坐标,来绘制一些不太好用直角坐标系绘制的曲线,让你认识极坐标的优点,从而帮助你掌握极坐标的用法。
|
|||
|
|
|
|||
|
|
## 如何用极坐标方程绘制曲线
|
|||
|
|
|
|||
|
|
在[第6节课](https://time.geekbang.org/column/article/256827)中,为了更方便地绘制曲线,我们用parametric.js函数实现了一个参数方程的绘图模块,它非常方便。所以在使用极坐标方程绘制曲线的时候,我们也要用到parametric.js函数。不过,在使用之前,我们还要对它进行扩展,让它支持坐标映射。这样,我们就可以写出对应的坐标映射函数,从而将极坐标映射为绘图需要的直角坐标了。
|
|||
|
|
|
|||
|
|
具体的操作就是,给parametric增加一个参数**rFunc**。rFunc是一个坐标映射函数,通过它我们可以将任意坐标映射为直角坐标,修改后的代码如下:
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
export function parametric(sFunc, tFunc, rFunc) {
|
|||
|
|
return function (start, end, seg = 100, ...args) {
|
|||
|
|
const points = [];
|
|||
|
|
for(let i = 0; i <= seg; i++) {
|
|||
|
|
const p = i / seg;
|
|||
|
|
const t = start * (1 - p) + end * p;
|
|||
|
|
const x = sFunc(t, ...args);
|
|||
|
|
const y = tFunc(t, ...args);
|
|||
|
|
if(rFunc) {
|
|||
|
|
points.push(rFunc(x, y));
|
|||
|
|
} else {
|
|||
|
|
points.push([x, y]);
|
|||
|
|
}
|
|||
|
|
}
|
|||
|
|
return {
|
|||
|
|
draw: draw.bind(null, points),
|
|||
|
|
points,
|
|||
|
|
};
|
|||
|
|
};
|
|||
|
|
}
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
看到这里,你可能想问,直角坐标和极坐标转换的函数,我们在一开始不是已经讲过了吗?为什么这里又要拓展一个rFunc参数呢?其实啊,开头我给出的函数虽然足够简单,但不够灵活,也不便于扩展。而先使用rFunc来抽象坐标映射,再把其他函数作为rFunc参数传给parametric,是一种更通用的坐标映射方法,它属于函数式编程思想。
|
|||
|
|
|
|||
|
|
说到这,我再多说几句。虽然函数式设计思想不是我们这个课程的核心,但它对框架和库的设计很重要,所以,我讲它也是希望你能通过这个例子,尽可能地理解代码中的精髓,学会使用最佳的设计方法和思路去解决问题,获得更多额外的收获,而不只是去理解眼前的基本概念。
|
|||
|
|
|
|||
|
|
那接下来,我们用极坐标参数方程画一个半径为200的半圆。在这里,我们把fromPolar作为rFunc参数传给parametric,就可以使用极坐标的参数方程来绘制图形了,代码如下所示。
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
const fromPolar = (r, θ) => {
|
|||
|
|
return [r * Math.cos(θ), r * Math.sin(θ)];
|
|||
|
|
};
|
|||
|
|
|
|||
|
|
const arc = parametric(
|
|||
|
|
t => 200,
|
|||
|
|
t => t,
|
|||
|
|
fromPolar,
|
|||
|
|
);
|
|||
|
|
|
|||
|
|
arc(0, Math.PI).draw(ctx);
|
|||
|
|
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
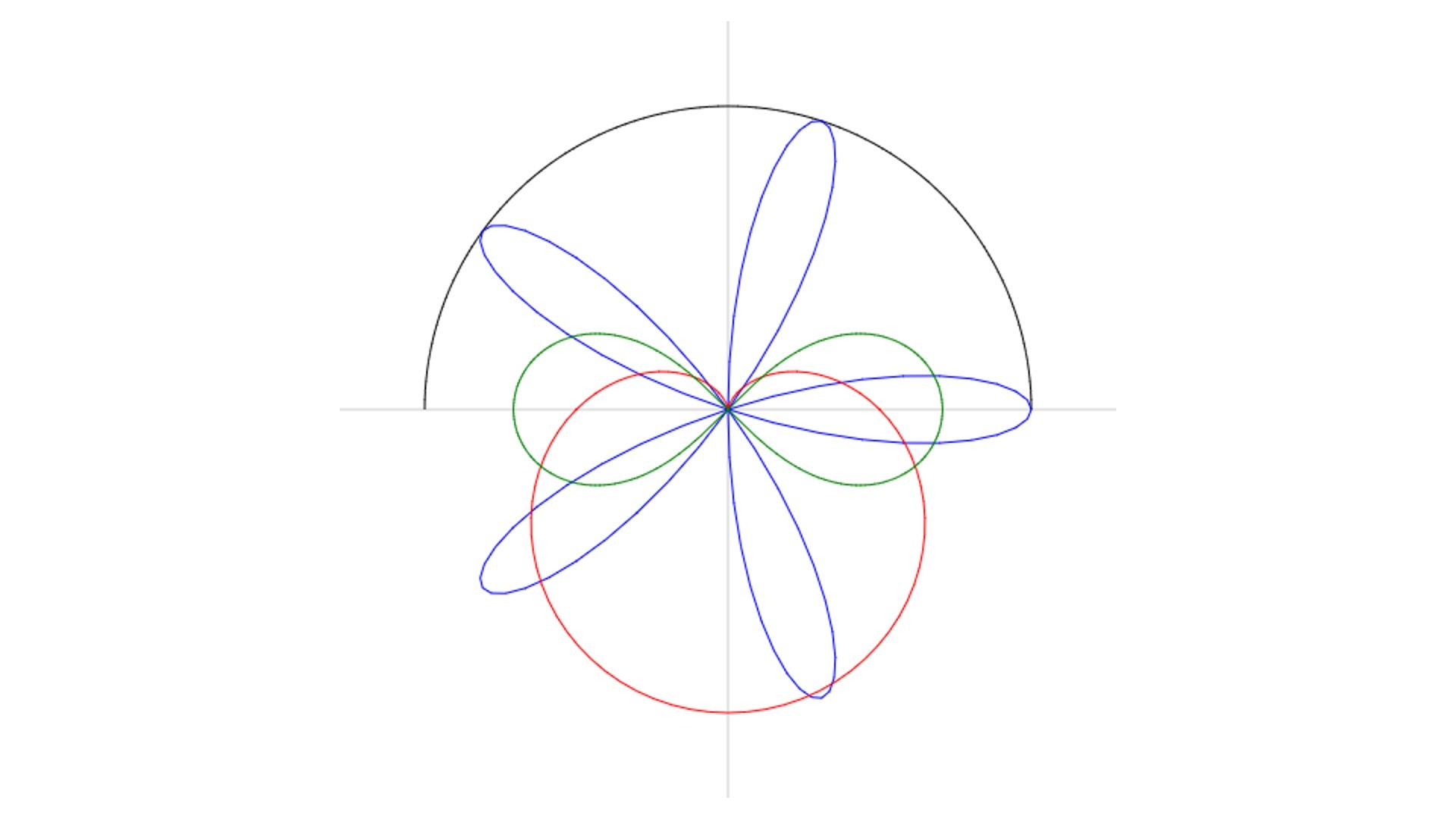
此外,我们还可以添加其他的极坐标参数方程来绘制更多曲线,比如玫瑰线、心形线或者双纽线。因为这些操作都比较简单,我就直接在下面给出代码了。
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
const rose = parametric(
|
|||
|
|
(t, a, k) => a * Math.cos(k * t),
|
|||
|
|
t => t,
|
|||
|
|
fromPolar,
|
|||
|
|
);
|
|||
|
|
|
|||
|
|
rose(0, Math.PI, 100, 200, 5).draw(ctx, {strokeStyle: 'blue'});
|
|||
|
|
|
|||
|
|
const heart = parametric(
|
|||
|
|
(t, a) => a - a * Math.sin(t),
|
|||
|
|
t => t,
|
|||
|
|
fromPolar,
|
|||
|
|
);
|
|||
|
|
|
|||
|
|
heart(0, 2 * Math.PI, 100, 100).draw(ctx, {strokeStyle: 'red'});
|
|||
|
|
|
|||
|
|
const foliumRight = parametric(
|
|||
|
|
(t, a) => Math.sqrt(2 * a ** 2 * Math.cos(2 * t)),
|
|||
|
|
t => t,
|
|||
|
|
fromPolar,
|
|||
|
|
);
|
|||
|
|
|
|||
|
|
const foliumLeft = parametric(
|
|||
|
|
(t, a) => -Math.sqrt(2 * a ** 2 * Math.cos(2 * t)),
|
|||
|
|
t => t,
|
|||
|
|
fromPolar,
|
|||
|
|
);
|
|||
|
|
|
|||
|
|
foliumRight(-Math.PI / 4, Math.PI / 4, 100, 100).draw(ctx, {strokeStyle: 'green'});
|
|||
|
|
foliumLeft(-Math.PI / 4, Math.PI / 4, 100, 100).draw(ctx, {strokeStyle: 'green'});
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
最终,我们能够绘制出如下的效果:
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
总的来说,我们看到,使用极坐标系中参数方程来绘制曲线的方法,其实和我们学过的直角坐标系中参数方程绘制曲线差不多,唯一的区别就是在具体实现的时候,我们需要额外增加一个坐标映射函数,将极坐标转为直角坐标才能完成最终的绘制。
|
|||
|
|
|
|||
|
|
## 如何使用片元着色器与极坐标系绘制图案?
|
|||
|
|
|
|||
|
|
在前面的例子中,我们主要还是通过参数方程来绘制曲线,用Canvas2D进行渲染。那如果我们使用shader来渲染,又该怎么使用极坐标系绘图呢?
|
|||
|
|
|
|||
|
|
这里,我们还是以圆为例,来看一下用shader渲染,再以极坐标画圆的做法。你可以先尝试自己理解下面的代码,然后再看我后面的讲解。
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
#ifdef GL_ES
|
|||
|
|
precision highp float;
|
|||
|
|
#endif
|
|||
|
|
|
|||
|
|
varying vec2 vUv;
|
|||
|
|
|
|||
|
|
vec2 polar(vec2 st) {
|
|||
|
|
return vec2(length(st), atan(st.y, st.x));
|
|||
|
|
}
|
|||
|
|
|
|||
|
|
void main() {
|
|||
|
|
vec2 st = vUv - vec2(0.5);
|
|||
|
|
st = polar(st);
|
|||
|
|
gl_FragColor.rgb = smoothstep(st.x, st.x + 0.01, 0.2) * vec3(1.0);
|
|||
|
|
gl_FragColor.a = 1.0;
|
|||
|
|
}
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
在上面的代码中,我们先通过坐标转换公式实现polar函数。这个函数作用是将直角坐标转换为极坐标,相当于课程一开始,我们用JavaScript写的toPolar函数。这里有一个细节需要注意,我们使用的是GLSL内置的float atan(float, float)方法,对应的方法是Math.atan,而在JavaScript版本的toPolar函数中,对应的方法是Math.atan2。
|
|||
|
|
|
|||
|
|
然后,我们将像素坐标转换为极坐标:st = polar(st); ,转换后的st.x实际上是极坐标的r分量,而st.y就是极坐标的θ分量。
|
|||
|
|
|
|||
|
|
我们知道,对于极坐标下过极点的圆,实际上的r值就是一个常量值,对应圆的半径,所以我们取smoothstep(st.x, st.x + 0.01, 0.2),就能得到一个半径为0.2的圆了。这一步,我们用的还是上节课的**距离场**方法。只不过,在直角坐标系下,点到圆心的距离d需要用x、y平方和的开方来计算,而在极坐标下,点的极坐标r值正好表示了点到圆心的距离d,所以计算起来就比直角坐标系简单了很多。
|
|||
|
|
|
|||
|
|
其实,我们无论是用直角坐标还是极坐标来画图,方法都差不多。但是,一些其他的曲线用极坐标绘制会很方便。比如说,要绘制玫瑰线,我们就可以用以下代码:
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
void main() {
|
|||
|
|
vec2 st = vUv - vec2(0.5);
|
|||
|
|
st = polar(st);
|
|||
|
|
float d = 0.5 * cos(st.y * 3.0) - st.x;
|
|||
|
|
gl_FragColor.rgb = smoothstep(-0.01, 0.01, d) * vec3(1.0);
|
|||
|
|
gl_FragColor.a = 1.0;
|
|||
|
|
}
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
这样,在画布上绘制出来的结果是三瓣玫瑰线:
|
|||
|
|
|
|||
|
|

|
|||
|
|
|
|||
|
|
可能你还是会有疑问,为什么d = 0.5 \* cos(st.y \* 3.0) - st.x; 绘制出的图形就是三瓣玫瑰线的图案呢?
|
|||
|
|
|
|||
|
|
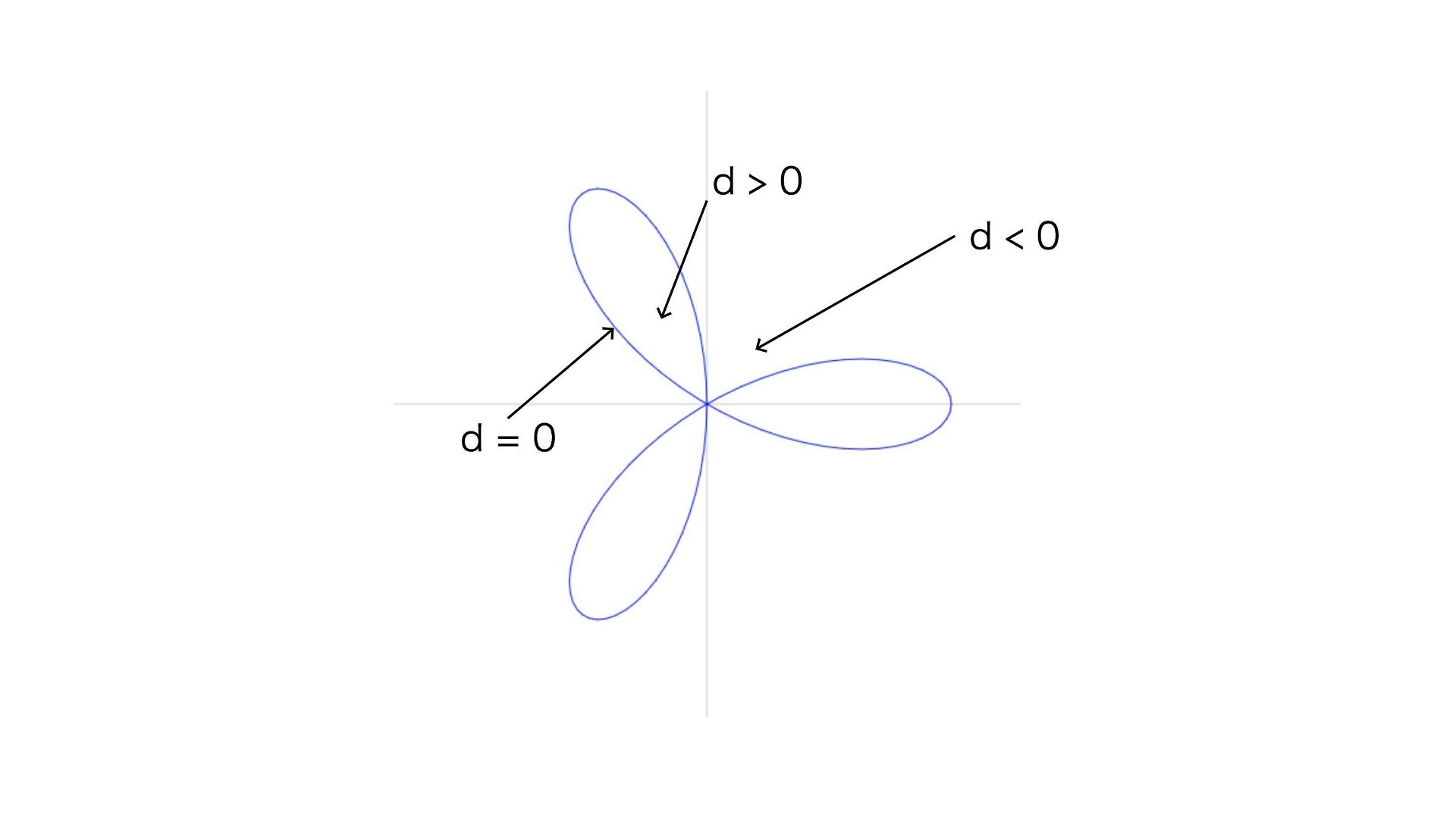
这是因为玫瑰线的极坐标方程r = a \* cos(k \* θ),所以玫瑰线上的所有点都满足0 = a \* cos(k \* θ) - r 这个方程式。如果我们再把它写成距离场的形式:d = a \* cos(k \* θ) - r。这个时候就有三种情况:玫瑰线上点的 d 等于 0;玫瑰线围出的图形外的点的 d 小于0,玫瑰线围出的图形内的点的 d 大于 0。
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
因此,smoothstep(-0.01, 0.01, d) 能够将 d >= 0,也就是玫瑰线内的点选出来,这样也就绘制出了三瓣图形。
|
|||
|
|
|
|||
|
|
那玫瑰线有什么用呢?它是一种很有趣图案,我们只要修改u\_k的值,并且保证它是正整数,就可以绘制出不同瓣数的玫瑰线图案。
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
uniform float u_k;
|
|||
|
|
|
|||
|
|
void main() {
|
|||
|
|
vec2 st = vUv - vec2(0.5);
|
|||
|
|
st = polar(st);
|
|||
|
|
float d = 0.5 * cos(st.y * u_k) - st.x;
|
|||
|
|
gl_FragColor.rgb = smoothstep(-0.01, 0.01, d) * vec3(1.0);
|
|||
|
|
gl_FragColor.a = 1.0;
|
|||
|
|
}
|
|||
|
|
|
|||
|
|
|
|||
|
|
renderer.uniforms.u_k = 3;
|
|||
|
|
|
|||
|
|
setInterval(() => {
|
|||
|
|
renderer.uniforms.u_k += 2;
|
|||
|
|
}, 200);
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|

|
|||
|
|
|
|||
|
|
类似的图案还有花瓣线:
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
void main() {
|
|||
|
|
vec2 st = vUv - vec2(0.5);
|
|||
|
|
st = polar(st);
|
|||
|
|
float d = 0.5 * abs(cos(st.y * u_k * 0.5)) - st.x;
|
|||
|
|
gl_FragColor.rgb = smoothstep(-0.01, 0.01, d) * vec3(1.0);
|
|||
|
|
gl_FragColor.a = 1.0;
|
|||
|
|
}
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
在u\_k=3的时候,我们可以得到如下图案:
|
|||
|
|
|
|||
|
|

|
|||
|
|
|
|||
|
|
有趣的是,它和玫瑰线不一样,u\_k的取值不一定要是整数。这让它能绘制出来的图形更加丰富,比如说我们可以取u\_k=1.3,这时得到的图案就像是一个横放的苹果。
|
|||
|
|
|
|||
|
|

|
|||
|
|
|
|||
|
|
在此基础上,我们还可以再添加几个uniform变量,如u\_scale、u\_offset作为参数,来绘制出更多图形。代码如下:
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
varying vec2 vUv;
|
|||
|
|
uniform float u_k;
|
|||
|
|
uniform float u_scale;
|
|||
|
|
uniform float u_offset;
|
|||
|
|
|
|||
|
|
void main() {
|
|||
|
|
vec2 st = vUv - vec2(0.5);
|
|||
|
|
st = polar(st);
|
|||
|
|
float d = u_scale * 0.5 * abs(cos(st.y * u_k * 0.5)) - st.x + u_offset;
|
|||
|
|
gl_FragColor.rgb = smoothstep(-0.01, 0.01, d) * vec3(1.0);
|
|||
|
|
gl_FragColor.a = 1.0;
|
|||
|
|
}
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
当我们取u\_k=1.7,u\_scale=0.5,u\_offset=0.2时,就能得到一个横置的葫芦图案。
|
|||
|
|
|
|||
|
|

|
|||
|
|
|
|||
|
|
如果我们继续修改 d 的计算方程,还能绘制出其他有趣的图形。
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
void main() {
|
|||
|
|
vec2 st = vUv - vec2(0.5);
|
|||
|
|
st = polar(st);
|
|||
|
|
float d = smoothstep(-0.3, 1.0, u_scale * 0.5 * cos(st.y * u_k) + u_offset) - st.x;
|
|||
|
|
gl_FragColor.rgb = smoothstep(-0.01, 0.01, d) * vec3(1.0);
|
|||
|
|
gl_FragColor.a = 1.0;
|
|||
|
|
}
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
比如,当继续修改 d 的计算方程时,我们可以绘制出花苞图案:
|
|||
|
|
|
|||
|
|

|
|||
|
|
|
|||
|
|
方法已经知道了,你可以在课后结合三角函数、abs、smoothstep,来尝试绘制一些更有趣的图案。如果有什么特别好玩的图案,你也可以分享出来。
|
|||
|
|
|
|||
|
|
## 极坐标系如何实现角向渐变?
|
|||
|
|
|
|||
|
|
除了绘制有趣的图案之外,极坐标的另一个应用是**角向渐变**(Conic Gradients)。那角向渐变是什么呢?如果你对CSS比较熟悉,一定知道角向渐变就是以图形中心为轴,顺时针地实现渐变效果。而且新的 [CSS Image Values and Replaced Content](https://www.w3.org/TR/css-images-4/#conic-gradients) 标准 level4 已经添加了角向渐变,我们可以使用它来创建一个基于极坐标的颜色渐变,代码如下:
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
div.conic {
|
|||
|
|
width: 150px;
|
|||
|
|
height: 150px;
|
|||
|
|
border-radius: 50%;
|
|||
|
|
background: conic-gradient(red 0%, green 45%, blue);
|
|||
|
|
}
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|

|
|||
|
|
|
|||
|
|
我们可以通过角向渐变创建一个颜色由角度过渡的元素。在WebGL中,我们可以通过极坐标用片元着色器实现类似的角向渐变效果,代码如下:
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
void main() {
|
|||
|
|
vec2 st = vUv - vec2(0.5);
|
|||
|
|
st = polar(st);
|
|||
|
|
float d = smoothstep(st.x, st.x + 0.01, 0.2);
|
|||
|
|
// 将角度范围转换到0到2pi之间
|
|||
|
|
if(st.y < 0.0) st.y += 6.28;
|
|||
|
|
// 计算p的值,也就是相对角度,p取值0到1
|
|||
|
|
float p = st.y / 6.28;
|
|||
|
|
if(p < 0.45) {
|
|||
|
|
// p取0到0.45时从红色线性过渡到绿色
|
|||
|
|
gl_FragColor.rgb = d * mix(vec3(1.0, 0, 0), vec3(0, 0.5, 0), p / 0.45);
|
|||
|
|
} else {
|
|||
|
|
// p超过0.45从绿色过渡到蓝色
|
|||
|
|
gl_FragColor.rgb = d * mix(vec3(0, 0.5, 0), vec3(0, 0, 1.0), (p - 0.45) / (1.0 - 0.45));
|
|||
|
|
}
|
|||
|
|
gl_FragColor.a = 1.0;
|
|||
|
|
}
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
如上面代码所示,我们将像素坐标转变为极坐标之后,st.y就是与x轴的夹角。因为polar函数里计算的atan(y, x)的取值范围是-π到π,所以我们在st.y小于0的时候,将它加上2π,这样就能把取值范围转换到0到2π了。
|
|||
|
|
|
|||
|
|
然后,我们根据角度换算出对应的比例对颜色进行线性插值。比如,比例在0%~45%之间,我们让颜色从红色过渡为绿色,那在45%到100%之间,我们让颜色从绿色过渡到蓝色。这样,我们最终就会得到如下效果:
|
|||
|
|
|
|||
|
|

|
|||
|
|
|
|||
|
|
这个效果与CSS角向渐变得到的基本上一致,除了CSS角向渐变的起始角度是与Y轴的夹角,而shader是与X轴的夹角以外,没有其他的不同。这样,我们就可以在WebGL中利用极坐标系实现与CSS角向渐变一致的视觉效果了。
|
|||
|
|
|
|||
|
|
## 极坐标如何绘制HSV色轮?
|
|||
|
|
|
|||
|
|
想要实现丰富的视觉效果离不开颜色,通过前面的课程,我们已经知道各种颜色的表示方法,为了更方便地调试颜色,我们可以进一步来实现色轮。什么是色轮呢?色轮可以帮助我们,把某种颜色表示法所能表示的所有颜色方便、直观地显示出来。
|
|||
|
|
|
|||
|
|
那在WebGL中,我们该怎么绘制HSV色轮呢?我们可以用极坐标结合HSV颜色来绘制它。
|
|||
|
|
|
|||
|
|
接下来,就让我们一起在片元着色器中实现它吧。实现的过程其实并不复杂,我们只需要将像素坐标转换为极坐标,再除以2π,就能得到HSV的H值。然后我们用鼠标位置的x、y坐标来决定S和V的值,完整的片元着色器代码如下:
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
#ifdef GL_ES
|
|||
|
|
precision highp float;
|
|||
|
|
#endif
|
|||
|
|
|
|||
|
|
varying vec2 vUv;
|
|||
|
|
uniform vec2 uMouse;
|
|||
|
|
|
|||
|
|
vec3 hsv2rgb(vec3 c){
|
|||
|
|
vec3 rgb = clamp(abs(mod(c.x*6.0+vec3(0.0,4.0,2.0), 6.0)-3.0)-1.0, 0.0, 1.0);
|
|||
|
|
rgb = rgb * rgb * (3.0 - 2.0 * rgb);
|
|||
|
|
return c.z * mix(vec3(1.0), rgb, c.y);
|
|||
|
|
}
|
|||
|
|
|
|||
|
|
vec2 polar(vec2 st) {
|
|||
|
|
return vec2(length(st), atan(st.y, st.x));
|
|||
|
|
}
|
|||
|
|
|
|||
|
|
void main() {
|
|||
|
|
vec2 st = vUv - vec2(0.5);
|
|||
|
|
st = polar(st);
|
|||
|
|
float d = smoothstep(st.x, st.x + 0.01, 0.2);
|
|||
|
|
if(st.y < 0.0) st.y += 6.28;
|
|||
|
|
float p = st.y / 6.28;
|
|||
|
|
gl_FragColor.rgb = d * hsv2rgb(vec3(p, uMouse.x, uMouse.y));
|
|||
|
|
gl_FragColor.a = 1.0;
|
|||
|
|
}
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
最终的效果如下图所示:
|
|||
|
|
|
|||
|
|

|
|||
|
|
|
|||
|
|
## 圆柱坐标与球坐标
|
|||
|
|
|
|||
|
|
最后,我还想和你说说极坐标和圆柱坐标系以及球坐标系之间的关系。我们知道极坐标系是二维坐标系,如果我们将极坐标系延z轴扩展,可以得到圆柱坐标系。圆柱坐标系是一种三维坐标系,可以用来绘制一些三维曲线,比如螺旋线、圆内螺旋线、费马曲线等等。
|
|||
|
|
|
|||
|
|
[](https://zh.wikipedia.org/)
|
|||
|
|
|
|||
|
|
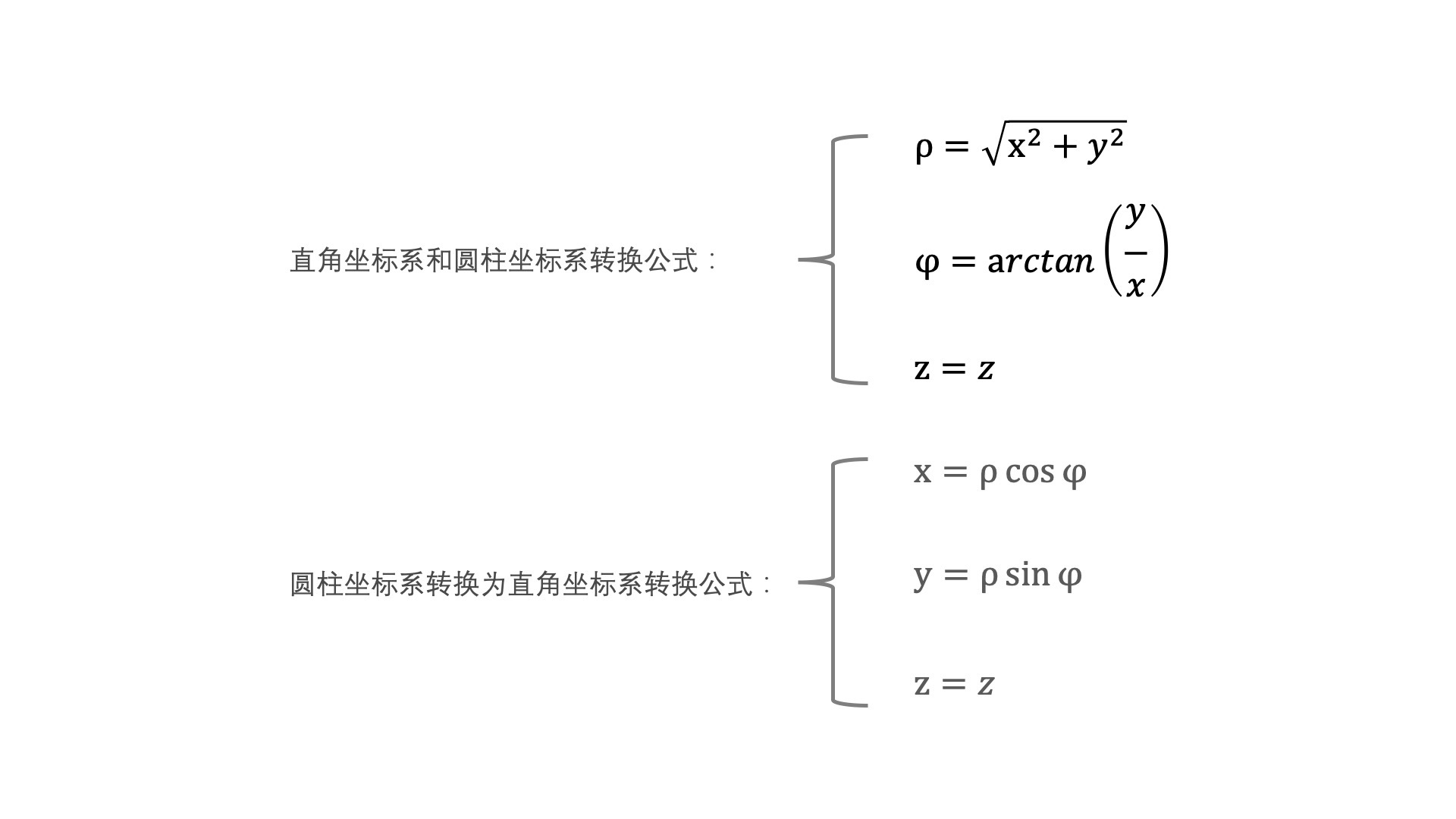
因为极坐标系可以和直角坐标系相互转换,所以直角坐标系和圆柱坐标系也可以相互转换,公式如下:
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
从上面的公式中你会发现,我们只转换了x、y的坐标,因为它们是极坐标,而z的坐标因为本身就是直角坐标不用转换。因此圆柱坐标系又被称为**半极坐标系。**
|
|||
|
|
|
|||
|
|
在此基础上,我们还可以进一步将圆柱坐标系转为球坐标系。
|
|||
|
|
|
|||
|
|
[](https://zh.wikipedia.org)
|
|||
|
|
|
|||
|
|
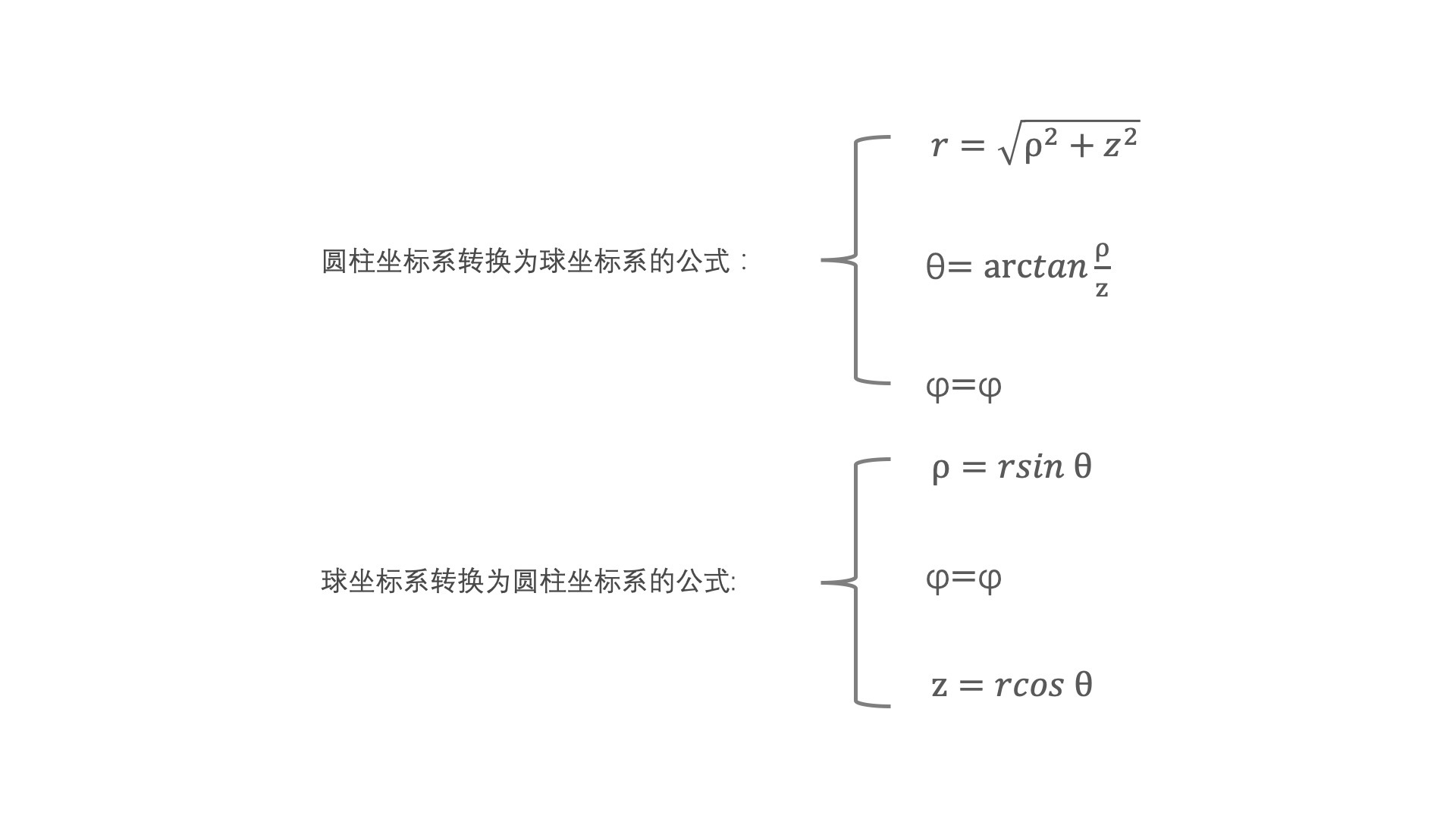
同样地,圆柱坐标系也可以和球坐标系相互转换,公式如下:
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
球坐标系在三维图形绘制、球面定位、碰撞检测等等可视化实现时都很有用,在后续的课程中,我们会有机会用到球坐标系,在这里你需要先记住它的转换公式。
|
|||
|
|
|
|||
|
|
## 要点总结
|
|||
|
|
|
|||
|
|
这一节课,我们学习了一个新的坐标系统也就是极坐标系,并且理解了直角坐标系与极坐标系的相互转换。
|
|||
|
|
|
|||
|
|
极坐标系是使用相对极点的距离,以及与x轴正向的夹角来表示点的坐标。极坐标系想要转换为直角坐标系需要用到fromPolar函数,反过来需要用到toPolar函数。
|
|||
|
|
|
|||
|
|
那在具体使用极坐标来绘制曲线的时候,有两种渲染方式。第一种是用Cavans渲染,这时候,我们可以用到之前学过的parametric高阶函数,将极坐标参数方程和坐标映射函数fromPolar传入,得到绘制曲线的函数,再用它来执行绘制。这样,极坐标系就能实现直角坐标系不太好描述的曲线了,比如,玫瑰线、心形线等等。
|
|||
|
|
|
|||
|
|
第二种是使用shader渲染,一般的方法是先将像素坐标转换为极坐标,然后使用极坐标构建距离场并着色。它能实现更多复杂的图案。
|
|||
|
|
|
|||
|
|
除了绘图,使用极坐标还可以实现角向渐变和HSV色轮。角向渐变通常可以用在构建饼图,而HSV色轮一般用在颜色可视化和择色交互等场合里。
|
|||
|
|
|
|||
|
|
此外,你还需要了解圆柱坐标、球坐标与直角坐标系的相互转换。在后续课程里,我们会使用圆柱坐标或球坐标来处理三维图形,到时候它们会非常有用。
|
|||
|
|
|
|||
|
|
## 小试牛刀
|
|||
|
|
|
|||
|
|
1. 用极坐标绘制小图案时,我们绘制了苹果和葫芦的图案,但它们是横置的。你可以试着修改它们,让它们的方向变为正向吗?具体怎么做呢?
|
|||
|
|
|
|||
|
|
2. 在角向渐变的例子中,CSS角向渐变是与Y轴的夹角,而使用着色器绘制的版本是与X轴的夹角。那如果要让着色器绘制版本的效果与CSS角向渐变效果完全一致,我们该怎么做呢?
|
|||
|
|
|
|||
|
|
3. 我们已经学过了随机数、距离场以及极坐标,你是不是可以利用它们绘制出一个画布,并且呈现随机的剪纸图案,类似的效果如下所示。
|
|||
|
|
|
|||
|
|
|
|||
|
|

|
|||
|
|
|
|||
|
|
欢迎在留言区和我讨论,分享你的答案和思考,也欢迎你把这节课分享给你的朋友,我们下节课再见!
|
|||
|
|
|
|||
|
|
* * *
|
|||
|
|
|
|||
|
|
## 源码
|
|||
|
|
|
|||
|
|
[parametric-shader](https://github.com/akira-cn/graphics/tree/master/parametric-polar)
|
|||
|
|
[ploar-shader](https://github.com/akira-cn/graphics/tree/master/polar-shader)
|
|||
|
|
|