255 lines
14 KiB
Markdown
255 lines
14 KiB
Markdown
|
|
# 19 | 图像分割(上):详解图像分割原理与图像分割模型
|
|||
|
|
|
|||
|
|
你好,我是方远。
|
|||
|
|
|
|||
|
|
在前两节课我们完成了有关图像分类的学习与实践。今天,让我们进入到计算机视觉另外一个非常重要的应用场景——图像分割。
|
|||
|
|
|
|||
|
|
你一定用过或听过腾讯会议或者Zoom之类的产品吧?在进行会议的时候,我们可以选择对背景进行替换,如下图所示。
|
|||
|
|
|
|||
|
|

|
|||
|
|
|
|||
|
|
在华为手机中也曾经有过人像留色的功能。
|
|||
|
|
|
|||
|
|

|
|||
|
|
|
|||
|
|
这些应用背后的实现都离不开今天要讲的图像分割。
|
|||
|
|
|
|||
|
|
我们同样用两节课的篇幅进行学习,这节课主攻分割原理,下节课再把这些技能点活用到实战上,从头开始搭建一个图像分割模型。
|
|||
|
|
|
|||
|
|
## 图像分割
|
|||
|
|
|
|||
|
|
我们不妨用对比的视角,先从概念理解一下图像分割是什么。图像分类是将一张图片自动分成某一类别,而图像分割是需要将图片中的每一个像素进行分类。
|
|||
|
|
|
|||
|
|
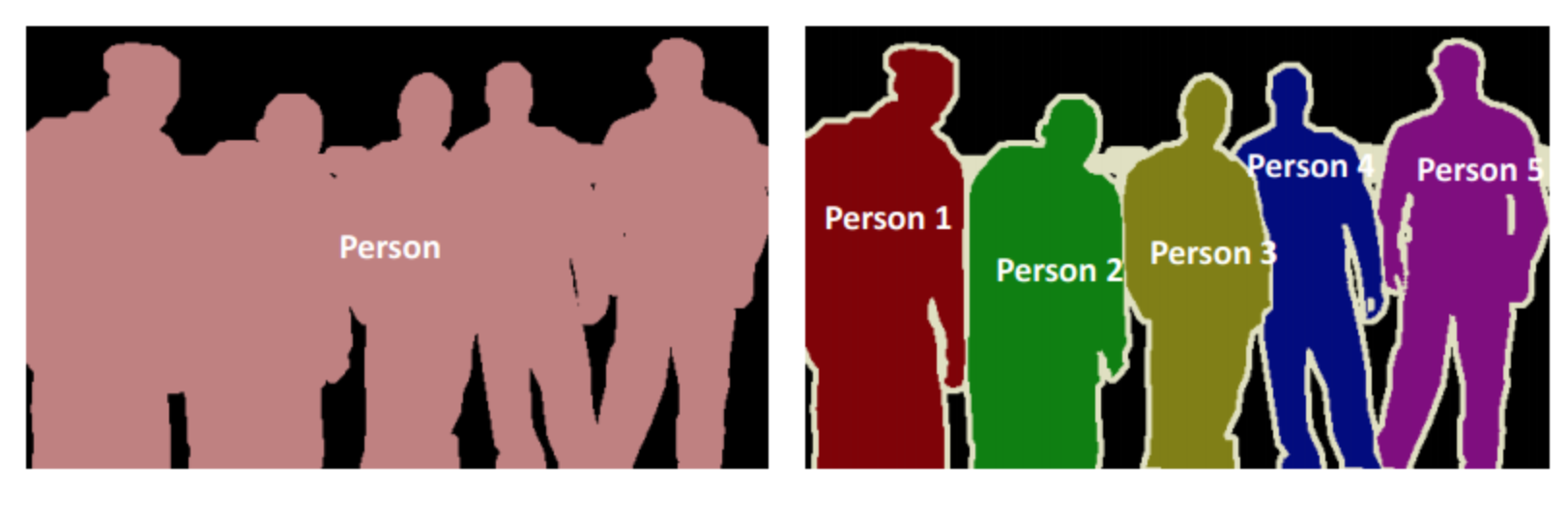
图像分割可以分为语义分割与实例分割,两者的区别是语义分割中只需要把每个像素点进行分类就可以了,不需要区分是否来自同一个实例,而实例分割不仅仅需要对像素点进行分类,还需要判断来自哪个实例。
|
|||
|
|
|
|||
|
|
如下图所示,左侧为语义分割,右侧为实例分割。我们这两节课都会以语义分割来展开讲解。
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
## 语义分割原理
|
|||
|
|
|
|||
|
|
语义分割原理其实与图像分类大致类似,主要有两点区别。首先是分类端(这是我自己起的名字,就是经过卷积提取特征后分类的那一块)不同,其次是网络结构有所不同。先看第一点,也就是分类端的不同。
|
|||
|
|
|
|||
|
|
### 分类端
|
|||
|
|
|
|||
|
|
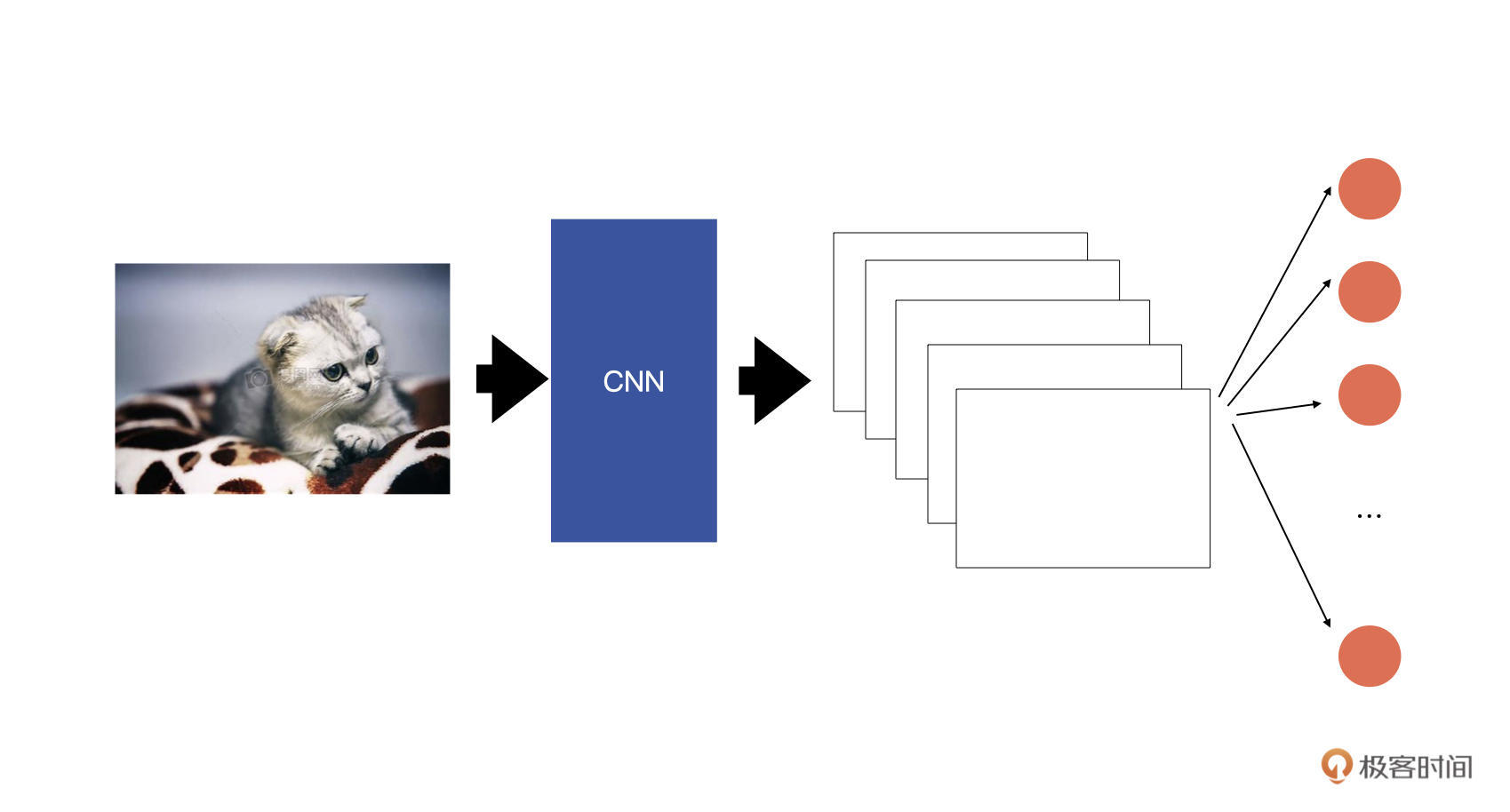
我们先回想一下图像分类的原理。你可以结合下面的示意图做理解。
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
输入图片经过卷积层提取特征后,最终会生成若干特征图,然后在这些特征图之后会接一个全连接层(上图中红色的圆圈),全连接层中的节点数就对应着要将图片分为几类。我们将全连接层的输出送入到softmax中,就可以获得每个类别的概率,然后通过概率就可以判断输入图片属于哪一个类别了。
|
|||
|
|
|
|||
|
|
在图像分割中,同样是利用卷积层来提取特征,最终生成若干特征图。只不过最后生成的特征图
|
|||
|
|
|
|||
|
|
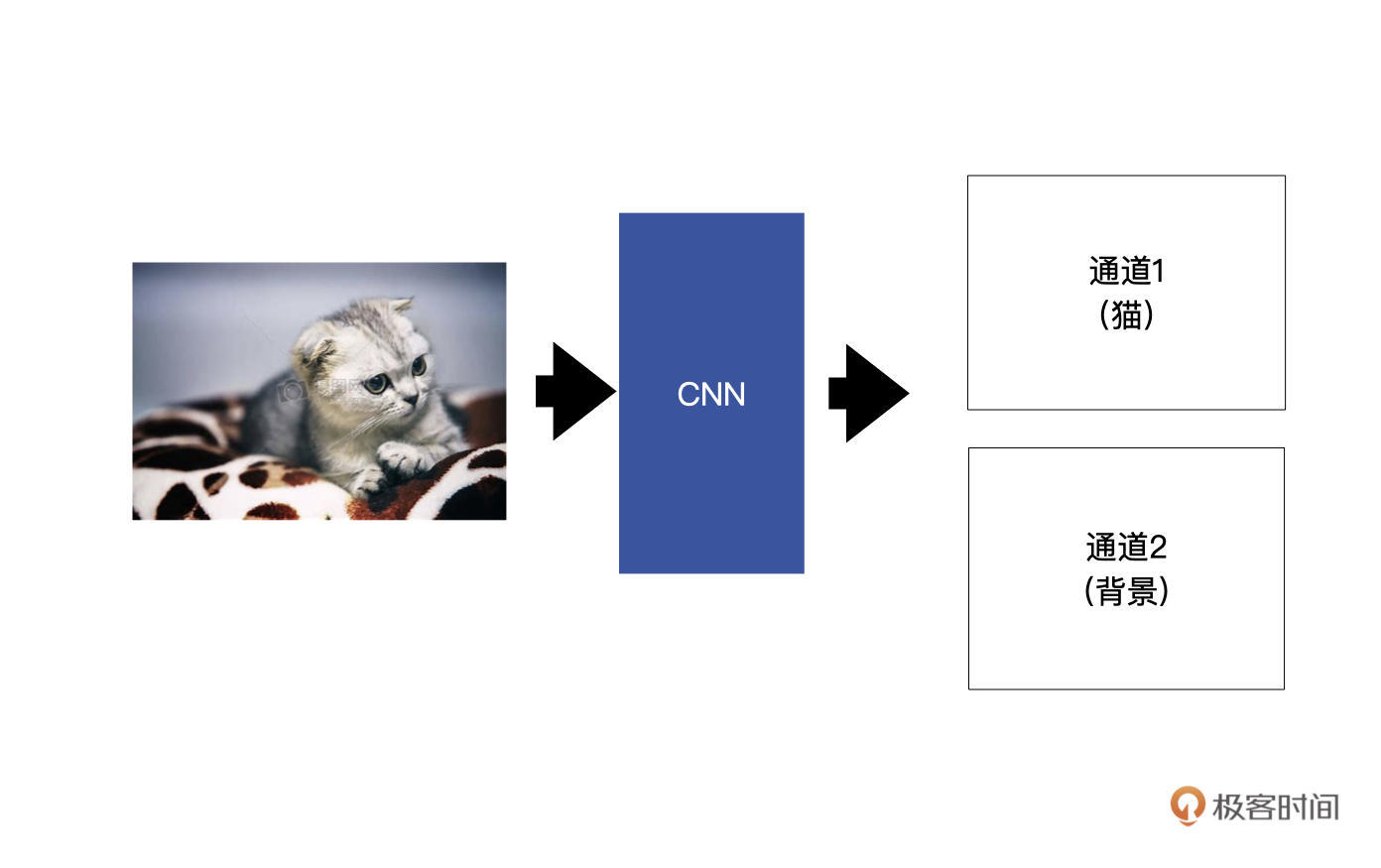
的数目对应着要分割成的类别数。举一个例子,假设我们想要将输入的小猫分割出来,也就是说,这个图像分割模型有两个类别,分别是小猫与背景,如下图所示。
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
最终的两个特征图中,通道1代表的小猫的信息,通道2对应着背景的信息。
|
|||
|
|
|
|||
|
|
这里我给你再举一个例子,来说明一下如何判断每个像素的类别。假设,通道1中(0,0)这个位置的输出是2,通道2中(0,0)这个位置的输出是30。
|
|||
|
|
|
|||
|
|
经过softmax转为概率后,通道1(0, 0)这个位置的概率为0,而对应通道2中(0,0)这个位置的概率为1,我们通过概率可以判断出,在(0,0)这个位置是背景,而不是小猫。
|
|||
|
|
|
|||
|
|
### 网络结构
|
|||
|
|
|
|||
|
|
在分割网络中最终输出的特征图的大小要么是与输入的原图相同,要么就是接近输入。
|
|||
|
|
|
|||
|
|
这么做的原因是,我们要对原图中的每个像素进行判断。当输出特征图与原图尺寸相同时,可以直接进行分割判断。当输出特征图与原图尺寸不相同时,需要将输出的特征图resize到原图大小。
|
|||
|
|
|
|||
|
|
如果是从一个比较小的特征图resize到一个比较大的尺寸的时候,必定会丢失掉一部分信息的。所以,输出特征图的大小不能太小。
|
|||
|
|
|
|||
|
|
这也是图像分割网络与图像分类网络的第二个不同点,在图像分类中,经过多层的特征提取,最后生成的特征图都是很小的。而**在图像分割中,最后生成的特征图通常来说是接近原图的**。
|
|||
|
|
|
|||
|
|
前文也说过,图像分割网络也是通过卷积进行提取特征的,按照之前的理论特征提取后,特征图尺寸是减小的。如果说把特征提取看做Encoder的话,那在图像分割中还有一步是Decoder。
|
|||
|
|
|
|||
|
|
Decoder的作用就是对特征图尺寸进行还原的过程,将尺寸还原到一个比较大的尺寸。这个还原的操作对应的就是上采样。而在上采样中我们通常使用的是转置卷积。
|
|||
|
|
|
|||
|
|
#### 转置卷积
|
|||
|
|
|
|||
|
|
接下来我就带你研究一下转置卷积的计算原理,这也是这节课的重点内容。
|
|||
|
|
|
|||
|
|
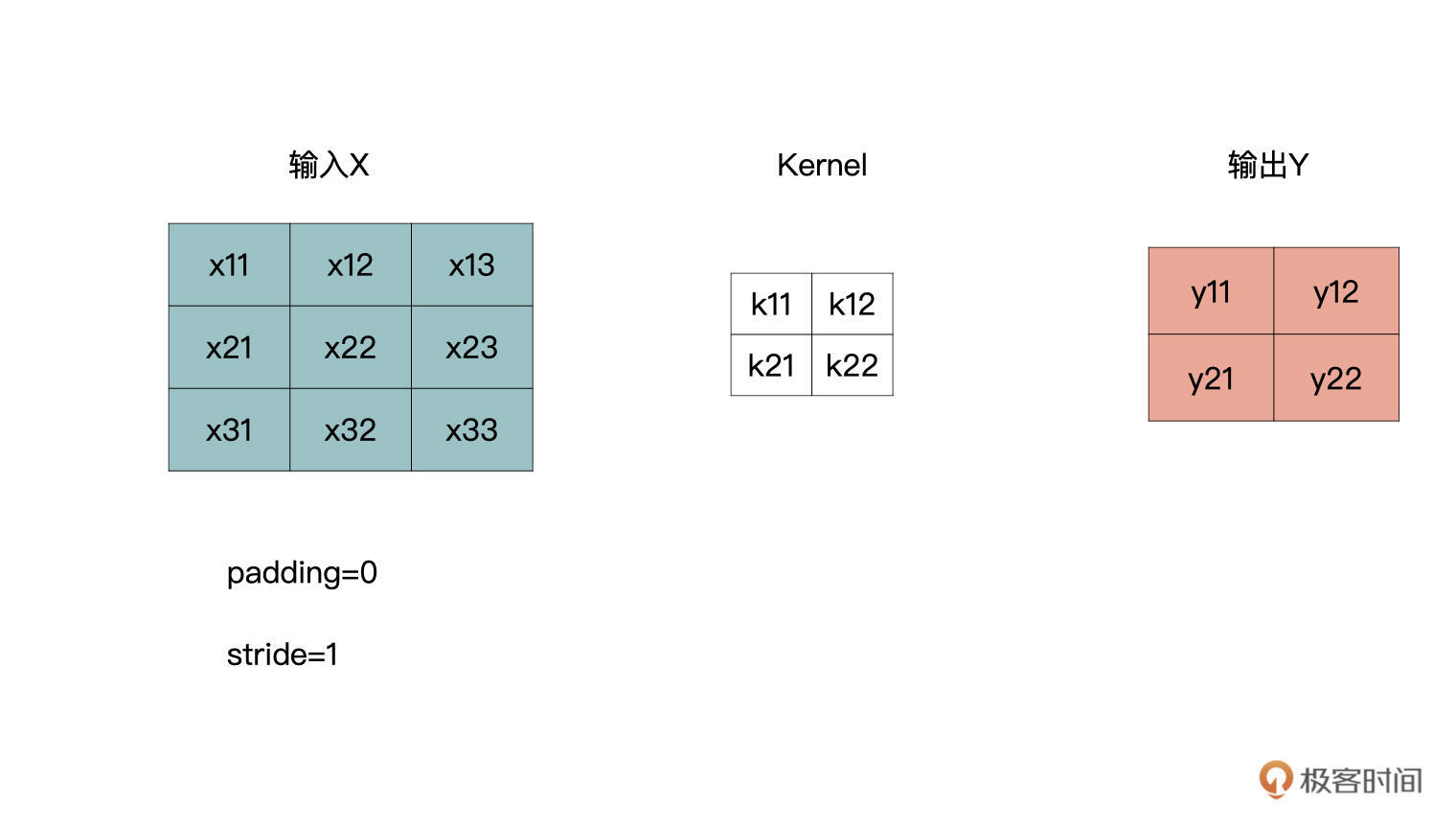
我们看下面图这个卷积计算,padding为0,stride为1。
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
从之前的学习我们可以知道,卷积操作是一个多对一的运算,输出中的每一个y都与输入中的4个x有关。其实,转置卷积从逻辑上是卷积的一个逆过程,而**不是卷积的逆运算。**
|
|||
|
|
|
|||
|
|
也就是说,转置卷积并不是使用上图中的输出Y与卷积核Kernel来获得上图中的输入X,转置卷积只能还原出一个与输入特征图**尺寸**相同的特征图。
|
|||
|
|
|
|||
|
|
我们将转置卷积中的卷积核用k’表示,那么一个y会与四个k’进行还原,如下所示:
|
|||
|
|
|
|||
|
|
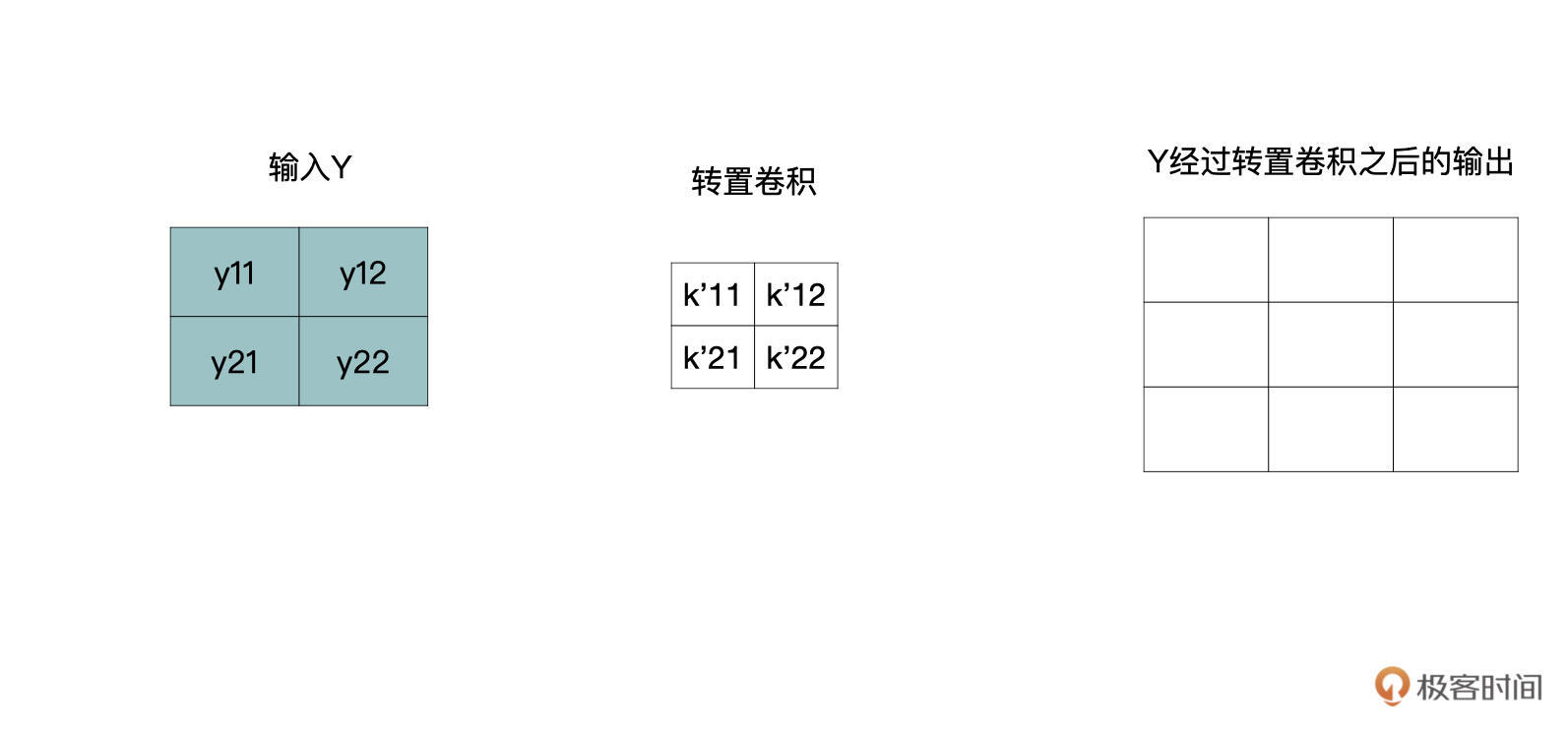
|
|||
|
|
|
|||
|
|
还原尺寸的过程如下所示,下图中每个还原后的结果都对应着原始3x3的输入。
|
|||
|
|
|
|||
|
|

|
|||
|
|
|
|||
|
|
通过观察你可以发现,有些部分是重合的,对于重合部分把它们加起来就可以了,最终还原后的特征图如下:
|
|||
|
|
|
|||
|
|
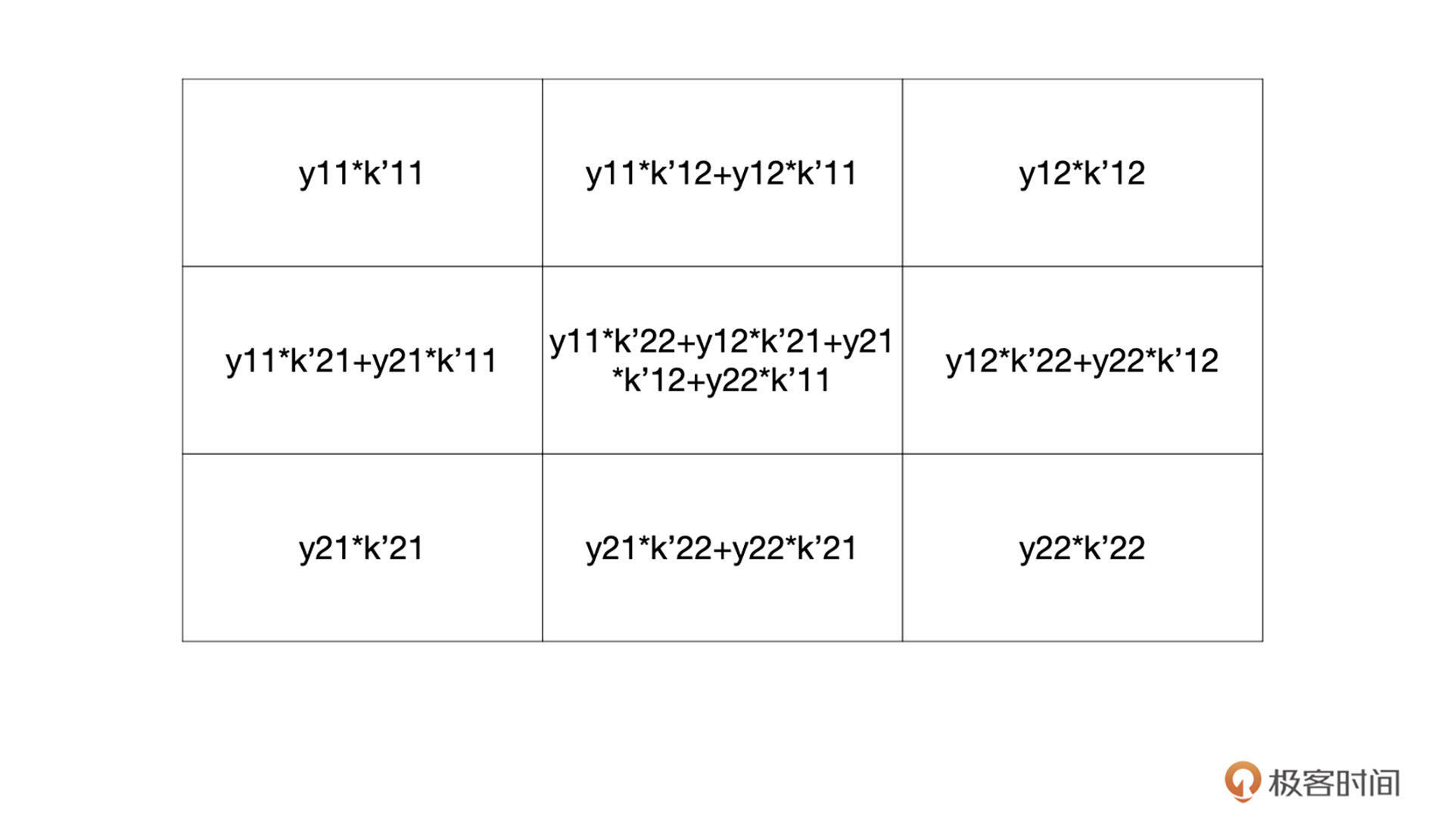
|
|||
|
|
|
|||
|
|
将上图的结果稍作整理,整理为下面的结果,也没有做什么特殊处理,只是补了一些零:
|
|||
|
|
|
|||
|
|

|
|||
|
|
|
|||
|
|
上面的结果,我们又可以通过下面的卷积获得:
|
|||
|
|
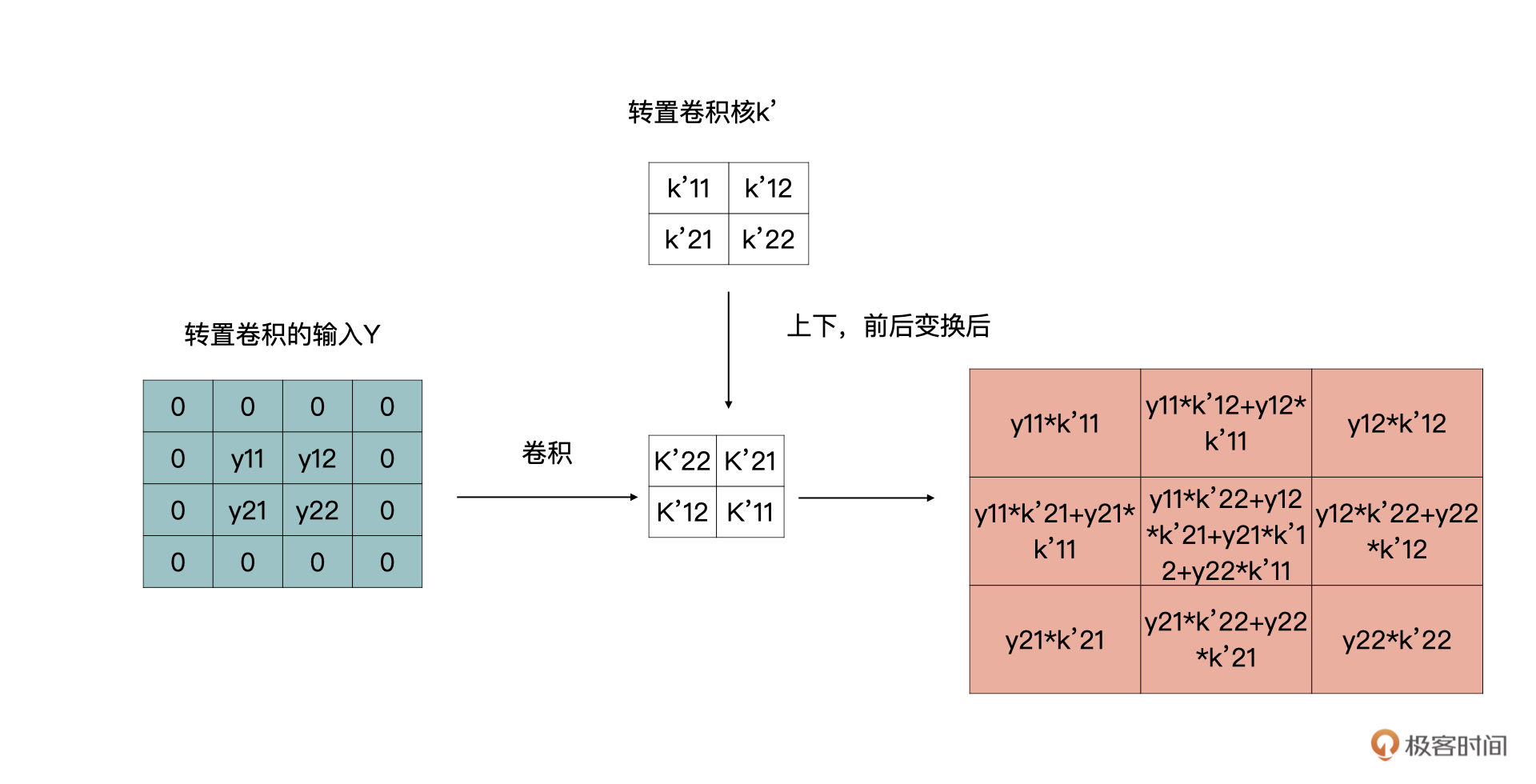
|
|||
|
|
|
|||
|
|
你有没有发现一件很神奇的事情,转置卷积计算又变回了卷积计算。
|
|||
|
|
|
|||
|
|
所以,我们一起梳理一下,转置卷积的计算过程如下:
|
|||
|
|
|
|||
|
|
1.对输入特征图进行补零操作。
|
|||
|
|
2.将转置卷积的卷积核上下、左右变换作为新的卷积核。
|
|||
|
|
3.利用新的卷积核在1的基础上进行**步长为1**,**padding为0**的卷积操作。
|
|||
|
|
|
|||
|
|
我们先来看一下,PyTorch中转置卷积以及它的主要参数,再根据参数解释一下第一步1是如何补零的。
|
|||
|
|
|
|||
|
|
```python
|
|||
|
|
class torch.nn.ConvTranspose2d(in_channels,
|
|||
|
|
out_channels,
|
|||
|
|
kernel_size,
|
|||
|
|
stride=1,
|
|||
|
|
padding=0,
|
|||
|
|
groups=1,
|
|||
|
|
bias=True,
|
|||
|
|
dilation=1)
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
其中,in\_channels、out\_channels、kernel\_size、groups、bias以及dilation与我们之前讲卷积时的参数含义是一样的(你可以回顾卷积的第[9](https://time.geekbang.org/column/article/432042)、[10](https://time.geekbang.org/column/article/433801)两节课),这里我们就不赘述了。
|
|||
|
|
|
|||
|
|
首先,我们看一下stride。因为转置卷积是卷积的一个逆向过程,所以这里的stride指的是在原图上的stride。
|
|||
|
|
|
|||
|
|
在我们刚才的例子里,stride是等于1的,如果等于2时,按照同样的套路,可以转换为如下的卷积变换。 同时,我们也可以得到结论,上文中第一步,补零的操作是,在输入的特征图的行与列之间补stride-1个行与列的零。
|
|||
|
|
|
|||
|
|
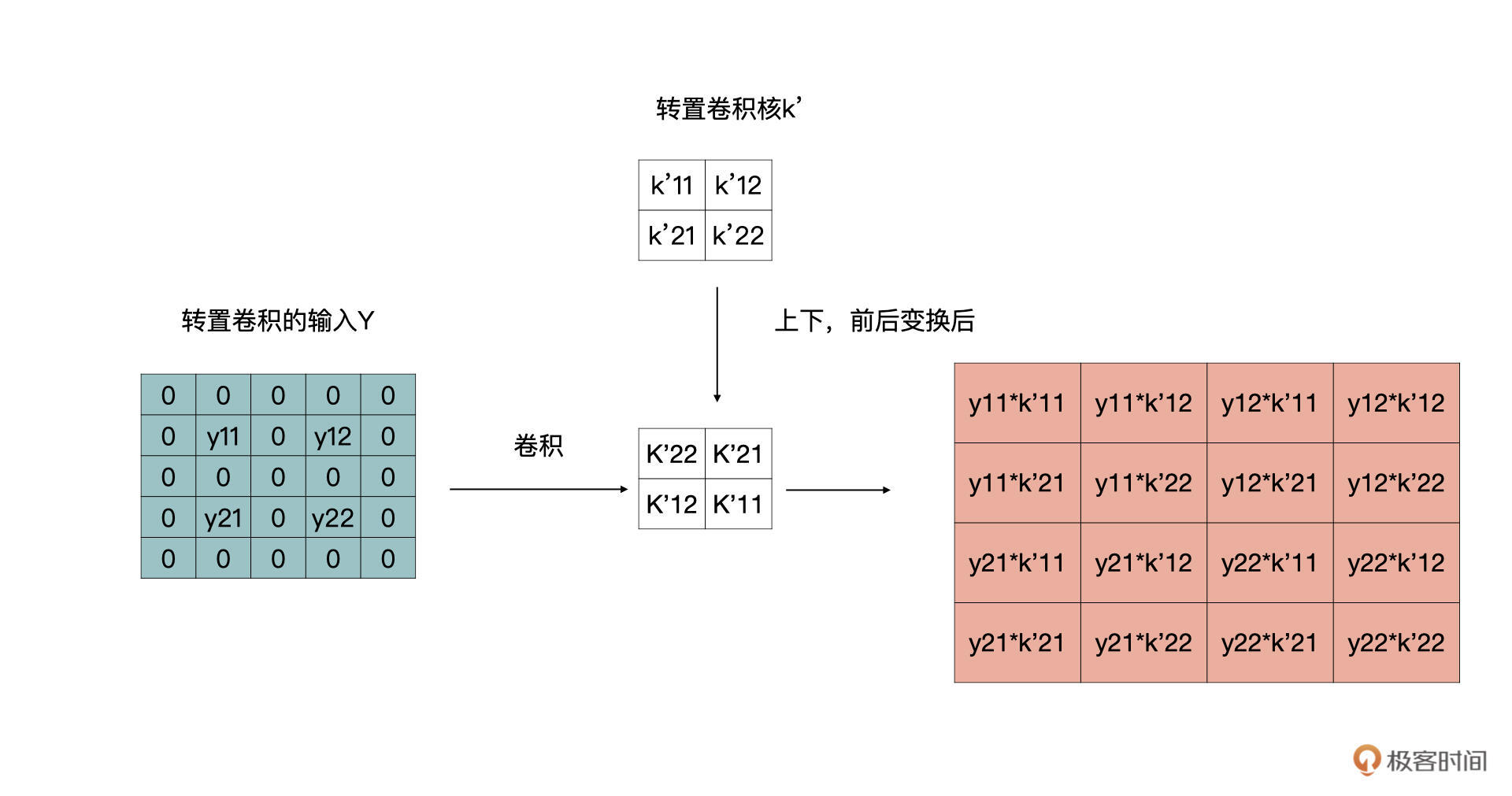
|
|||
|
|
|
|||
|
|
再来看padding操作,padding是指要在输入特征图的周围补dilation \* (kernel\_size - 1) - padding圈零。这里用到了dliation参数,但是通常在转置卷积中dilation、groups参数使用的比较少。
|
|||
|
|
|
|||
|
|
以上就是转置卷积的补零操作了,图片和文字双管齐下,我相信你一定能够理解它。
|
|||
|
|
|
|||
|
|
通过上述的讲解,我们可以推导出输出特征图尺寸与输入特征图尺寸的关系:
|
|||
|
|
|
|||
|
|
$$h\_{out} = (h\_{in} - 1) \* stride\[0\] - padding\[0\] + kernel\\\_size\[0\]$$
|
|||
|
|
|
|||
|
|
$$w\_{out} = (w\_{in} - 1) \* stride\[1\] - padding\[1\] + kernel\\\_size\[1\]$$
|
|||
|
|
|
|||
|
|
下面,我们借助代码来验证一下,我们讲的转置卷积是否是向我们所说的那样计算。
|
|||
|
|
|
|||
|
|
现在有特征图input\_feat:
|
|||
|
|
|
|||
|
|
```python
|
|||
|
|
import torch
|
|||
|
|
import torch.nn as nn
|
|||
|
|
import numpy as np
|
|||
|
|
input_feat = torch.tensor([[[[1, 2], [3, 4]]]], dtype=torch.float32)
|
|||
|
|
input_feat
|
|||
|
|
输出:
|
|||
|
|
tensor([[[[1., 2.],
|
|||
|
|
[3., 4.]]]])
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
卷积核k:
|
|||
|
|
|
|||
|
|
```python
|
|||
|
|
kernels = torch.tensor([[[[1, 0], [1, 1]]]], dtype=torch.float32)
|
|||
|
|
kernels
|
|||
|
|
输出:
|
|||
|
|
tensor([[[[1., 0.],
|
|||
|
|
[1., 1.]]]])
|
|||
|
|
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
stride为1,padding为0的转置卷积:
|
|||
|
|
|
|||
|
|
```python
|
|||
|
|
convTrans = nn.ConvTranspose2d(1, 1, kernel_size=2, stride=1, padding=0, bias = False)
|
|||
|
|
convTrans.weight=nn.Parameter(kernels)
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
按照我们刚才讲的,第一步是补零操作,输入的特征图补零后为:
|
|||
|
|
|
|||
|
|
$$input\\\_feat = \\begin{bmatrix}
|
|||
|
|
0 & 0 & 0 & 0 \\\\\\
|
|||
|
|
0 & 1 & 2 & 0 \\\\\\
|
|||
|
|
0 & 3 & 4 & 0 \\\\\\
|
|||
|
|
0 & 0 & 0 & 0\\\\\\
|
|||
|
|
\\end{bmatrix} $$
|
|||
|
|
|
|||
|
|
然后再与变换后的卷积核:
|
|||
|
|
$$\\begin{bmatrix}
|
|||
|
|
1 & 1 \\\\\\
|
|||
|
|
0 & 1
|
|||
|
|
\\end{bmatrix}$$
|
|||
|
|
做卷积运算后,获得输出:
|
|||
|
|
$$output = \\begin{bmatrix}
|
|||
|
|
1 & 2 & 0 \\\\\\
|
|||
|
|
4 & 7 & 2 \\\\\\
|
|||
|
|
3 & 7 & 4
|
|||
|
|
\\end{bmatrix} $$
|
|||
|
|
|
|||
|
|
我们再看看代码的输出,如下所示:
|
|||
|
|
|
|||
|
|
```python
|
|||
|
|
convTrans(input_feat)
|
|||
|
|
输出:
|
|||
|
|
tensor([[[[1., 2., 0.],
|
|||
|
|
[4., 7., 2.],
|
|||
|
|
[3., 7., 4.]]]], grad_fn=<SlowConvTranspose2DBackward>)
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
你看看是不是一样呢?
|
|||
|
|
|
|||
|
|
### 损失函数
|
|||
|
|
|
|||
|
|
说完网络结构,我们再开启图像分割里的另一个话题:损失函数。
|
|||
|
|
|
|||
|
|
在图像分割中依然可以使用在图像分类中经常使用的交叉熵损失。在图像分类中,一张图片有一个预测结果,预测结果与真实值就可以计算出一个Loss。而在图像分割中,真实的标签是一张二维特征图,这张特征图记录着每个像素的真实分类结果。在分割中,含有像素类别的特征图,我们一般称为Mask。
|
|||
|
|
|
|||
|
|
我们结合一张小猫图片的例子解释一下。对于下图中的小猫进行标记,标记后会生成它的GT,这个GT就是一个Mask。
|
|||
|
|
|
|||
|
|
GT是Ground Truth的缩写,在图像分割中我们经常使用这个词。在图像分类中与之对应的就是数据的真实标签,在图像分割中则GT是每个像素的真实分类,如下面的例子所示。
|
|||
|
|
|
|||
|
|

|
|||
|
|
|
|||
|
|
GT如下所示:
|
|||
|
|
|
|||
|
|

|
|||
|
|
|
|||
|
|
那在我们模型预测的Mask中,每个位置都会有一个预测结果,这个预测结果与GT中的Mask做比较,然后会生成一个Loss。
|
|||
|
|
|
|||
|
|
当然,在图像分割中不光有交叉熵损失可以用,还可以用更加有针对性的Dice Loss,下节课我再继续展开。
|
|||
|
|
|
|||
|
|
#### 公开数据集
|
|||
|
|
|
|||
|
|
刚才我们也看到了,图像分割的数据标注还是比较耗时的,具体如何标注一张语义分割所需要的图片,下节课我们再一起通过实践探索。
|
|||
|
|
|
|||
|
|
除此之外业界也有很多比较有权威性且质量很高的公开数据集。最著名的就是COCO了,链接如下:[https://cocodataset.org/#detection-2016](https://cocodataset.org/#detection-2016)。一共有80个类别,超过2万张图片。感兴趣的话,课后你可以尝试着使用它训练来看看。
|
|||
|
|
|
|||
|
|

|
|||
|
|
|
|||
|
|
## 小结
|
|||
|
|
|
|||
|
|
恭喜你完成了今天的学习。
|
|||
|
|
|
|||
|
|
今天我们首先明确了语义分割要解决的问题是什么,它可以对图像中的每个像素都进行分类。
|
|||
|
|
|
|||
|
|
然后我们对比图像分类原理,说明了语义分割的原理。它与图像分类主要有两个不同点:
|
|||
|
|
|
|||
|
|
1.在分类端有所不同,在图像分类中,经过卷积的特征提取后,最后会以若干个神经元的形式作为输出,每个神经元代表着对一个类别的判断情况。而语义分割,则是会输出若干的特征图,每个特征图代表着对应类别判断。
|
|||
|
|
|
|||
|
|
2.在图像分类的网络中,特征图是不断减小的。但是在语义分割的网络中,特征图还会有decoder这一步,它是将特征图进行放大的过程。实现decoder的方式称为上采样,在上采样中我们最常使用的就是转置卷积。
|
|||
|
|
|
|||
|
|
对于转置卷积,我们除了要知道它是怎么计算的之外,最重要的是要记住**它不是卷积的逆运算,只是能将特征图的大小进行放大的一种卷积运算**。
|
|||
|
|
|
|||
|
|
## 每课一练
|
|||
|
|
|
|||
|
|
对于本文的小猫分割问题,最终只输出1个特征图是否可以?
|
|||
|
|
|
|||
|
|
欢迎你在留言区跟我交流互动,也推荐你把这节课分享给更多同事、朋友。
|
|||
|
|
|