472 lines
18 KiB
Markdown
472 lines
18 KiB
Markdown
|
|
# 05 | Tensor变形记:快速掌握Tensor切分、变形等方法
|
|||
|
|
|
|||
|
|
你好,我是方远。
|
|||
|
|
|
|||
|
|
上节课我们一起学习了Tensor的基础概念,也熟悉了创建、转换、维度变换等操作,掌握了这些基础知识,你就可以做一些简单的Tensor相关的操作了。
|
|||
|
|
|
|||
|
|
不过,要想在实际的应用中更灵活地用好Tensor,Tensor的连接、切分等操作也是必不可少的。今天这节课,咱们就通过一些例子和图片来一块学习下。虽然这几个操作比较有难度,但只要你耐心听我讲解,然后上手练习,还是可以拿下的。
|
|||
|
|
|
|||
|
|
## Tensor的连接操作
|
|||
|
|
|
|||
|
|
在项目开发中,深度学习某一层神经元的数据可能有多个不同的来源,那么就需要将数据进行组合,这个组合的操作,我们称之为**连接**。
|
|||
|
|
|
|||
|
|
### cat
|
|||
|
|
|
|||
|
|
连接的操作函数如下。
|
|||
|
|
|
|||
|
|
```python
|
|||
|
|
torch.cat(tensors, dim = 0, out = None)
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
cat是concatnate的意思,也就是拼接、联系的意思。该函数有两个重要的参数需要你掌握。
|
|||
|
|
|
|||
|
|
第一个参数是tensors,它很好理解,就是若干个我们准备进行拼接的Tensor。
|
|||
|
|
|
|||
|
|
第二个参数是dim,我们回忆一下Tensor的定义,Tensor的维度(秩)是有多种情况的。比如有两个3维的Tensor,可以有几种不同的拼接方式(如下图),dim参数就可以对此作出约定。
|
|||
|
|
|
|||
|
|

|
|||
|
|
|
|||
|
|
看到这里,你可能觉得上面画的图是三维的,看起来比较晦涩,所以咱们先从简单的二维的情况说起,我们先声明两个3x3的矩阵,代码如下:
|
|||
|
|
|
|||
|
|
```python
|
|||
|
|
>>> A=torch.ones(3,3)
|
|||
|
|
>>> B=2*torch.ones(3,3)
|
|||
|
|
>>> A
|
|||
|
|
tensor([[1., 1., 1.],
|
|||
|
|
[1., 1., 1.],
|
|||
|
|
[1., 1., 1.]])
|
|||
|
|
>>> B
|
|||
|
|
tensor([[2., 2., 2.],
|
|||
|
|
[2., 2., 2.],
|
|||
|
|
[2., 2., 2.]])
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
我们先看看dim=0的情况,拼接的结果是怎样的:
|
|||
|
|
|
|||
|
|
```python
|
|||
|
|
>>> C=torch.cat((A,B),0)
|
|||
|
|
>>> C
|
|||
|
|
tensor([[1., 1., 1.],
|
|||
|
|
[1., 1., 1.],
|
|||
|
|
[1., 1., 1.],
|
|||
|
|
[2., 2., 2.],
|
|||
|
|
[2., 2., 2.],
|
|||
|
|
[2., 2., 2.]])
|
|||
|
|
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
你会发现,两个矩阵是按照“行”的方向拼接的。
|
|||
|
|
|
|||
|
|
我们接下来再看看,dim=1的情况是怎样的:
|
|||
|
|
|
|||
|
|
```python
|
|||
|
|
>>> D=torch.cat((A,B),1)
|
|||
|
|
>>> D
|
|||
|
|
tensor([[1., 1., 1., 2., 2., 2.],
|
|||
|
|
[1., 1., 1., 2., 2., 2.],
|
|||
|
|
[1., 1., 1., 2., 2., 2.]])
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
显然,两个矩阵,是按照“列”的方向拼接的。那如果Tensor是三维甚至更高维度的呢?其实道理也是一样的,dim的数值是多少,两个矩阵就会按照相应维度的方向链接两个Tensor。
|
|||
|
|
|
|||
|
|
看到这里你可能会问了,cat实际上是将多个Tensor在已有的维度上进行连接,那如果想增加新的维度进行连接,又该怎么做呢?这时候就需要stack函数登场了。
|
|||
|
|
|
|||
|
|
### stack
|
|||
|
|
|
|||
|
|
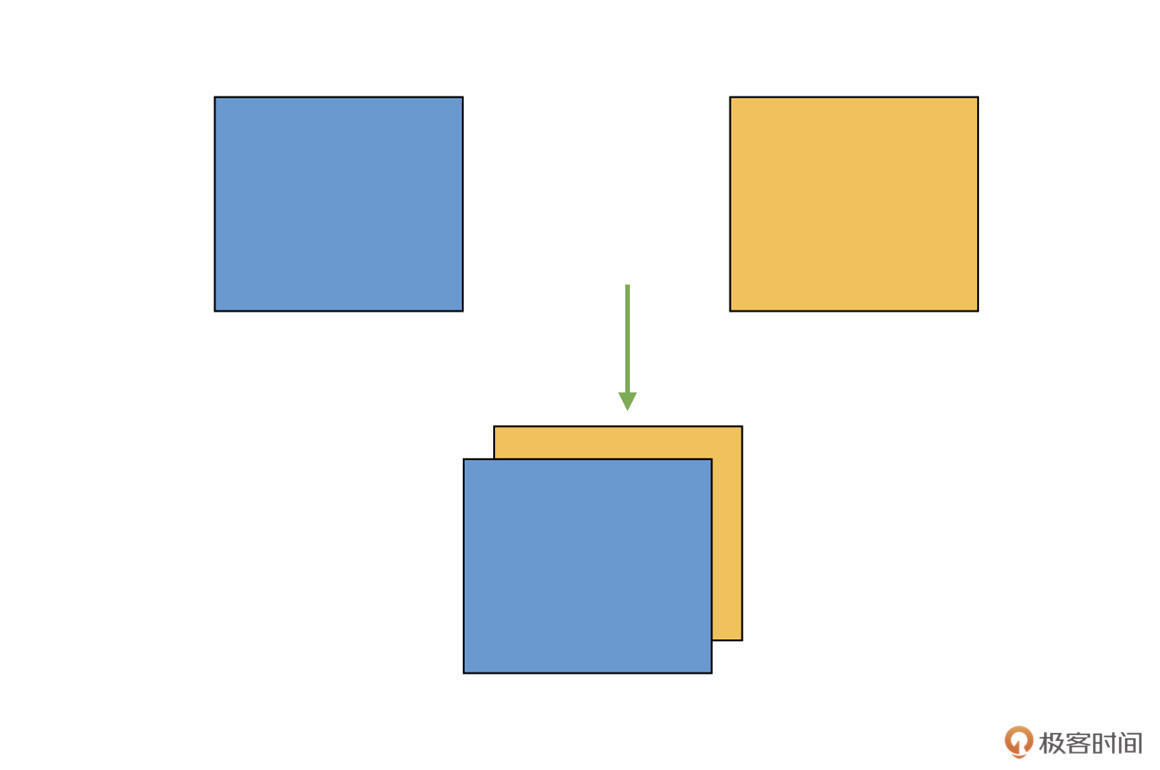
为了让你加深理解,我们还是结合具体例子来看看。假设我们有两个二维矩阵Tensor,把它们“堆叠”放在一起,构成一个三维的Tensor,如下图:
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
这相当于原来的维度(秩)是2,现在变成了3,变成了一个立体的结构,增加了一个维度。你需要注意的是,这跟前面的cat不同,cat中示意图的例子,原来就是3维的,cat之后仍旧是3维的,而现在咱们是**从2维变成了3维**。
|
|||
|
|
|
|||
|
|
在实际图像算法开发中,咱们有时候需要将多个单通道Tensor(2维)合并,得到多通道的结果(3维)。而实现这种增加维度拼接的方法,我们把它叫做stack。
|
|||
|
|
|
|||
|
|
stack函数的定义如下:
|
|||
|
|
|
|||
|
|
```python
|
|||
|
|
torch.stack(inputs, dim=0)
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
其中,inputs表示需要拼接的Tensor,dim表示新建立维度的方向。
|
|||
|
|
|
|||
|
|
那stack如何使用呢?我们一块来看一个例子:
|
|||
|
|
|
|||
|
|
```python
|
|||
|
|
>>> A=torch.arange(0,4)
|
|||
|
|
>>> A
|
|||
|
|
tensor([0, 1, 2, 3])
|
|||
|
|
>>> B=torch.arange(5,9)
|
|||
|
|
>>> B
|
|||
|
|
tensor([5, 6, 7, 8])
|
|||
|
|
>>> C=torch.stack((A,B),0)
|
|||
|
|
>>> C
|
|||
|
|
tensor([[0, 1, 2, 3],
|
|||
|
|
[5, 6, 7, 8]])
|
|||
|
|
>>> D=torch.stack((A,B),1)
|
|||
|
|
>>> D
|
|||
|
|
tensor([[0, 5],
|
|||
|
|
[1, 6],
|
|||
|
|
[2, 7],
|
|||
|
|
[3, 8]])
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
结合代码,我们可以看到,首先我们构建了两个4元素向量A和B,它们的维度是1。然后,我们在dim=0,也就是“行”的方向上新建一个维度,这样维度就成了2,也就得到了C。而对于D,我们则是在dim=1,也就是“列”的方向上新建维度。
|
|||
|
|
|
|||
|
|
## Tensor的切分操作
|
|||
|
|
|
|||
|
|
学完了连接操作之后,我们再来看看连接的逆操作:**切分**。
|
|||
|
|
|
|||
|
|
切分就是连接的逆过程,有了刚才的经验,你很容易就会想到,切分的操作也应该有很多种,比如切片、切块等。没错,切分的操作主要分为三种类型:chunk、split、unbind。
|
|||
|
|
|
|||
|
|
乍一看有不少,其实是因为它们各有特点,适用于不同的使用情景,让我们一起看一下。
|
|||
|
|
|
|||
|
|
### chunk
|
|||
|
|
|
|||
|
|
chunk的作用就是将Tensor按照声明的dim,进行尽可能平均的划分。
|
|||
|
|
|
|||
|
|
比如说,我们有一个32channel的特征,需要将其按照channel均匀分成4组,每组8个channel,这个切分就可以通过chunk函数来实现。具体函数如下:
|
|||
|
|
|
|||
|
|
```python
|
|||
|
|
torch.chunk(input, chunks, dim=0)
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
我们挨个来看看函数中涉及到的三个参数:
|
|||
|
|
|
|||
|
|
首先是input,它表示要做chunk操作的Tensor。
|
|||
|
|
|
|||
|
|
接着,我们看下chunks,它代表将要被划分的块的数量,而不是每组的数量。请注意,**chunks必须是整型**。
|
|||
|
|
|
|||
|
|
最后是dim,想想这个参数是什么意思呢?对,就是按照哪个维度来进行chunk。
|
|||
|
|
|
|||
|
|
还是跟之前一样,我们通过几个代码例子直观感受一下。我们从一个简单的一维向量开始:
|
|||
|
|
|
|||
|
|
```python
|
|||
|
|
>>> A=torch.tensor([1,2,3,4,5,6,7,8,9,10])
|
|||
|
|
>>> B = torch.chunk(A, 2, 0)
|
|||
|
|
>>> B
|
|||
|
|
(tensor([1, 2, 3, 4, 5]), tensor([ 6, 7, 8, 9, 10]))
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
这里我们通过chunk函数,将原来10位长度的Tensor A,切分成了两个一样5位长度的向量。(注意,B是两个切分结果组成的tuple)。
|
|||
|
|
|
|||
|
|
那如果chunk参数不能够整除的话,结果会是怎样的呢?我们接着往下看:
|
|||
|
|
|
|||
|
|
```python
|
|||
|
|
>>> B = torch.chunk(A, 3, 0)
|
|||
|
|
>>> B
|
|||
|
|
(tensor([1, 2, 3, 4]), tensor([5, 6, 7, 8]), tensor([ 9, 10]))
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
我们发现,10位长度的Tensor A,切分成了三个向量,长度分别是4,4,2位。这是怎么分的呢,不应该是3,3,4这样更为平均的方式么?
|
|||
|
|
|
|||
|
|
想要解决问题,就得找到规律。让我们再来看一个更大一点的例子,将A改为17位长度。
|
|||
|
|
|
|||
|
|
```python
|
|||
|
|
>>> A=torch.tensor([1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17])
|
|||
|
|
>>> B = torch.chunk(A, 4, 0)
|
|||
|
|
>>> B
|
|||
|
|
(tensor([1, 2, 3, 4, 5]), tensor([ 6, 7, 8, 9, 10]), tensor([11, 12, 13, 14, 15]), tensor([16, 17]))
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
17位长度的Tensor A,切分成了四个分别为5,5,5,2位长度的向量。这时候你就会发现,其实在计算每个结果元素个数的时候,chunk函数是先做除法,然后再向上取整得到每组的数量。
|
|||
|
|
|
|||
|
|
比如上面这个例子,17/4=4.25,向上取整就是5,那就先逐个生成若干个长度为5的向量,最后不够的就放在一块,作为最后一个向量(长度2)。
|
|||
|
|
|
|||
|
|
那如果chunk参数大于Tensor可以切分的长度,又要怎么办呢?我们实际操作一下,代码如下:
|
|||
|
|
|
|||
|
|
```python
|
|||
|
|
>>> A=torch.tensor([1,2,3])
|
|||
|
|
>>> B = torch.chunk(A, 5, 0)
|
|||
|
|
>>> B
|
|||
|
|
(tensor([1]), tensor([2]), tensor([3]))
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
显然,被切分的Tensor只能分成若干个长度为1的向量。
|
|||
|
|
|
|||
|
|
由此可以推论出二维的情况,我们再举一个例子, 看看二维矩阵Tensor的情况 :
|
|||
|
|
|
|||
|
|
```python
|
|||
|
|
>>> A=torch.ones(4,4)
|
|||
|
|
>>> A
|
|||
|
|
tensor([[1., 1., 1., 1.],
|
|||
|
|
[1., 1., 1., 1.],
|
|||
|
|
[1., 1., 1., 1.],
|
|||
|
|
[1., 1., 1., 1.]])
|
|||
|
|
>>> B = torch.chunk(A, 2, 0)
|
|||
|
|
>>> B
|
|||
|
|
(tensor([[1., 1., 1., 1.],
|
|||
|
|
[1., 1., 1., 1.]]),
|
|||
|
|
tensor([[1., 1., 1., 1.],
|
|||
|
|
[1., 1., 1., 1.]]))
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
还是跟前面的cat一样,这里的dim参数,表示的是第dim维度方向上进行切分。
|
|||
|
|
|
|||
|
|
刚才介绍的chunk函数,是按照“切分成确定的份数”来进行切分的,那如果想按照“每份按照确定的大小”来进行切分,该怎样做呢?PyTorch也提供了相应的方法,叫做split。
|
|||
|
|
|
|||
|
|
### split
|
|||
|
|
|
|||
|
|
split的函数定义如下,跟前面一样,我们还是分别看看这里涉及的参数。
|
|||
|
|
|
|||
|
|
```python
|
|||
|
|
torch.split(tensor, split_size_or_sections, dim=0)
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
首先是tensor,也就是待切分的Tensor。
|
|||
|
|
|
|||
|
|
然后是split\_size\_or\_sections这个参数。当它为整数时,表示将tensor按照每块大小为这个整数的数值来切割;当这个参数为列表时,则表示将此tensor切成和列表中元素一样大小的块。
|
|||
|
|
|
|||
|
|
最后同样是dim,它定义了要按哪个维度切分。
|
|||
|
|
|
|||
|
|
同样的,我们举几个例子来看一下split的具体操作。首先是split\_size\_or\_sections是整数的情况。
|
|||
|
|
|
|||
|
|
```python
|
|||
|
|
>>> A=torch.rand(4,4)
|
|||
|
|
>>> A
|
|||
|
|
tensor([[0.6418, 0.4171, 0.7372, 0.0733],
|
|||
|
|
[0.0935, 0.2372, 0.6912, 0.8677],
|
|||
|
|
[0.5263, 0.4145, 0.9292, 0.5671],
|
|||
|
|
[0.2284, 0.6938, 0.0956, 0.3823]])
|
|||
|
|
>>> B=torch.split(A, 2, 0)
|
|||
|
|
>>> B
|
|||
|
|
(tensor([[0.6418, 0.4171, 0.7372, 0.0733],
|
|||
|
|
[0.0935, 0.2372, 0.6912, 0.8677]]),
|
|||
|
|
tensor([[0.5263, 0.4145, 0.9292, 0.5671],
|
|||
|
|
[0.2284, 0.6938, 0.0956, 0.3823]]))
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
在这个例子里,我们看到,原来4x4大小的Tensor A,沿着第0维度,也就是沿“行”的方向,按照每组2“行”的大小进行切分,得到了两个2x4大小的Tensor。
|
|||
|
|
|
|||
|
|
那么问题来了,如果split\_size\_or\_sections不能整除对应方向的大小的话,会有怎样的结果呢?我们将代码稍作修改就好了:
|
|||
|
|
|
|||
|
|
```python
|
|||
|
|
>>> C=torch.split(A, 3, 0)
|
|||
|
|
>>> C
|
|||
|
|
(tensor([[0.6418, 0.4171, 0.7372, 0.0733],
|
|||
|
|
[0.0935, 0.2372, 0.6912, 0.8677],
|
|||
|
|
[0.5263, 0.4145, 0.9292, 0.5671]]),
|
|||
|
|
tensor([[0.2284, 0.6938, 0.0956, 0.3823]]))
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
根据刚才的代码我们就能发现,原来,PyTorch会尽可能凑够每一个结果,使得其对应dim的数据大小等于split\_size\_or\_sections。如果最后剩下的不够,那就把剩下的内容放到一块,作为最后一个结果。
|
|||
|
|
|
|||
|
|
接下来,我们再看一下split\_size\_or\_sections是列表时的情况。刚才提到了,当split\_size\_or\_sections为列表的时候,表示将此tensor切成和列表中元素大小一样的大小的块,我们来看一段对应的代码:
|
|||
|
|
|
|||
|
|
```python
|
|||
|
|
>>> A=torch.rand(5,4)
|
|||
|
|
>>> A
|
|||
|
|
tensor([[0.1005, 0.9666, 0.5322, 0.6775],
|
|||
|
|
[0.4990, 0.8725, 0.5627, 0.8360],
|
|||
|
|
[0.3427, 0.9351, 0.7291, 0.7306],
|
|||
|
|
[0.7939, 0.3007, 0.7258, 0.9482],
|
|||
|
|
[0.7249, 0.7534, 0.0027, 0.7793]])
|
|||
|
|
>>> B=torch.split(A,(2,3),0)
|
|||
|
|
>>> B
|
|||
|
|
(tensor([[0.1005, 0.9666, 0.5322, 0.6775],
|
|||
|
|
[0.4990, 0.8725, 0.5627, 0.8360]]),
|
|||
|
|
tensor([[0.3427, 0.9351, 0.7291, 0.7306],
|
|||
|
|
[0.7939, 0.3007, 0.7258, 0.9482],
|
|||
|
|
[0.7249, 0.7534, 0.0027, 0.7793]]))
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
这部分代码怎么解释呢?其实也很好理解,就是将Tensor A,沿着第0维进行切分,每一个结果对应维度上的尺寸或者说大小,分别是2(行),3(行)。
|
|||
|
|
|
|||
|
|
### unbind
|
|||
|
|
|
|||
|
|
通过学习前面的几个函数,咱们知道了怎么按固定大小做切分,或者按照索引index来进行选择。现在我们想象一个应用场景,如果我们现在有一个3 channel图像的Tensor,想要逐个获取每个channel的数据,该怎么做呢?
|
|||
|
|
|
|||
|
|
假如用chunk的话,我们需要将chunks设为3;如果用split的话,需要将split\_size\_or\_sections设为1。
|
|||
|
|
|
|||
|
|
虽然它们都可以实现相同的目的,但是如果channel数量很大,逐个去取也比较折腾。这时候,就需要用到另一个函数:unbind,它的函数定义如下:
|
|||
|
|
|
|||
|
|
```python
|
|||
|
|
torch.unbind(input, dim=0)
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
其中,input表示待处理的Tensor,dim还是跟前面的函数一样,表示切片的方向。
|
|||
|
|
|
|||
|
|
我们结合例子来理解:
|
|||
|
|
|
|||
|
|
```python
|
|||
|
|
>>> A=torch.arange(0,16).view(4,4)
|
|||
|
|
>>> A
|
|||
|
|
tensor([[ 0, 1, 2, 3],
|
|||
|
|
[ 4, 5, 6, 7],
|
|||
|
|
[ 8, 9, 10, 11],
|
|||
|
|
[12, 13, 14, 15]])
|
|||
|
|
>>> b=torch.unbind(A, 0)
|
|||
|
|
>>> b
|
|||
|
|
(tensor([0, 1, 2, 3]),
|
|||
|
|
tensor([4, 5, 6, 7]),
|
|||
|
|
tensor([ 8, 9, 10, 11]),
|
|||
|
|
tensor([12, 13, 14, 15]))
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
在这个例子中,我们首先创建了一个4x4的二维矩阵Tensor,随后我们从第0维,也就是“行”的方向进行切分 ,因为矩阵有4行,所以就会得到4个结果。
|
|||
|
|
|
|||
|
|
接下来,我们看一下:如果从第1维,也就是“列”的方向进行切分,会是怎样的结果呢:
|
|||
|
|
|
|||
|
|
```python
|
|||
|
|
>>> b=torch.unbind(A, 1)
|
|||
|
|
>>> b
|
|||
|
|
(tensor([ 0, 4, 8, 12]),
|
|||
|
|
tensor([ 1, 5, 9, 13]),
|
|||
|
|
tensor([ 2, 6, 10, 14]),
|
|||
|
|
tensor([ 3, 7, 11, 15]))
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
不难发现,这里是按照“列”的方向进行拆解的。所以,**unbind是一种降维切分的方式**,相当于删除一个维度之后的结果。
|
|||
|
|
|
|||
|
|
## Tensor的索引操作
|
|||
|
|
|
|||
|
|
你有没有发现,刚才我们讲的chunk和split操作,我们都是将数据整体进行切分,并获得全部结果。但有的时候,我们只需要其中的一部分,这要怎么做呢?一个很自然的想法就是,直接告诉Tensor我想要哪些部分,这种方法我们称为索引操作。
|
|||
|
|
|
|||
|
|
索引操作有很多方式,有提供好现成API的,也有用户自行定制的操作,其中最常用的两个操作就是index\_select和masked\_select,我们分别去看看用法。
|
|||
|
|
|
|||
|
|
### index\_select
|
|||
|
|
|
|||
|
|
这里就需要index\_select这个函数了,其定义如下:
|
|||
|
|
|
|||
|
|
```python
|
|||
|
|
torch.index_select(tensor, dim, index)
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
这里的tensor、dim跟前面函数里的一样,不再赘述。我们重点看一看index,它表示从dim维度中的哪些位置选择数据,这里需要注意,index**是torch.Tensor类型**。
|
|||
|
|
|
|||
|
|
还是跟之前一样,我们来看几个示例代码:
|
|||
|
|
|
|||
|
|
```python
|
|||
|
|
>>> A=torch.arange(0,16).view(4,4)
|
|||
|
|
>>> A
|
|||
|
|
tensor([[ 0, 1, 2, 3],
|
|||
|
|
[ 4, 5, 6, 7],
|
|||
|
|
[ 8, 9, 10, 11],
|
|||
|
|
[12, 13, 14, 15]])
|
|||
|
|
>>> B=torch.index_select(A,0,torch.tensor([1,3]))
|
|||
|
|
>>> B
|
|||
|
|
tensor([[ 4, 5, 6, 7],
|
|||
|
|
[12, 13, 14, 15]])
|
|||
|
|
>>> C=torch.index_select(A,1,torch.tensor([0,3]))
|
|||
|
|
>>> C
|
|||
|
|
tensor([[ 0, 3],
|
|||
|
|
[ 4, 7],
|
|||
|
|
[ 8, 11],
|
|||
|
|
[12, 15]])
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
在这个例子中,我们先创建了一个4x4大小的矩阵Tensor A。然后,我们从第0维选择第1(行)和3(行)的数据,并得到了最终的Tensor B,其大小为2x4。随后我们从Tensor A中选择第0(列)和3(列)的数据,得到了最终的Tensor C,其大小为4x2。
|
|||
|
|
|
|||
|
|
怎么样,是不是非常简单?
|
|||
|
|
|
|||
|
|
### masked\_select
|
|||
|
|
|
|||
|
|
刚才介绍的indexed\_select,它是基于给定的索引来进行数据提取的。但有的时候,我们还想通过一些判断条件来进行选择,比如提取深度学习网络中某一层中数值大于0的参数。
|
|||
|
|
|
|||
|
|
这时候,就需要用到PyTorch提供的masked\_select函数了,我们先来看它的定义:
|
|||
|
|
|
|||
|
|
```python
|
|||
|
|
torch.masked_select(input, mask, out=None)
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
这里我们只需要关心前两个参数,input和mask。
|
|||
|
|
|
|||
|
|
input表示待处理的Tensor。mask代表掩码张量,也就是满足条件的特征掩码。这里你需要注意的是,mask须跟input张量有相同数量的元素数目,但形状或维度不需要相同。
|
|||
|
|
|
|||
|
|
你是不是还感觉有些云里雾里?让我来举一个例子,你看了之后,一下子就能明白。
|
|||
|
|
|
|||
|
|
你在平时的练习中有没有想过,如果我们让Tensor和数字做比较,会有什么样的结果?比如后面这段代码,我们随机生成一个5位长度的Tensor A:
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
>>> A=torch.rand(5)
|
|||
|
|
>>> A
|
|||
|
|
tensor([0.3731, 0.4826, 0.3579, 0.4215, 0.2285])
|
|||
|
|
>>> B=A>0.3
|
|||
|
|
>>> B
|
|||
|
|
tensor([ True, True, True, True, False])
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
在这段代码里,我们让A跟0.3做比较,得到了一个新的Tensor,内部每一个数值表示的是A中对应数值是否大于0.3。
|
|||
|
|
|
|||
|
|
比如第一个数值原来是0.3731,大于0.3,所以是True;最后一个数值0.2285小于0.3,所以是False。
|
|||
|
|
|
|||
|
|
这个新的Tensor其实就是一个掩码张量,它的每一位表示了一个判断条件是否成立的结果。
|
|||
|
|
|
|||
|
|
然后,我们继续写一段代码,看看基于掩码B的选择是怎样的结果 :
|
|||
|
|
|
|||
|
|
```python
|
|||
|
|
>>> C=torch.masked_select(A, B)
|
|||
|
|
>>> C
|
|||
|
|
tensor([0.3731, 0.4826, 0.3579, 0.4215])
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
你会发现,C实际上得到的就是:A中“**满足B里面元素值为True的”**对应位置的数据。
|
|||
|
|
|
|||
|
|
好了,这下你应该知道了masked\_select的作用了吧?其实就是我们根据要筛选的条件,得到一个掩码张量,然后用这个张量去提取Tensor中的数据。
|
|||
|
|
|
|||
|
|
根据这个思路,上面的例子就可以简化为:
|
|||
|
|
|
|||
|
|
```python
|
|||
|
|
>>> A=torch.rand(5)
|
|||
|
|
>>> A
|
|||
|
|
tensor([0.3731, 0.4826, 0.3579, 0.4215, 0.2285])
|
|||
|
|
>>> C=torch.masked_select(A, A>0.3)
|
|||
|
|
>>> C
|
|||
|
|
tensor([0.3731, 0.4826, 0.3579, 0.4215])
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
是不是非常简单呢?
|
|||
|
|
|
|||
|
|
## 小结
|
|||
|
|
|
|||
|
|
恭喜你完成了这节课的学习。这节课,我们一同学习了Tensor里更加高级的操作,包括Tensor之间的连接操作,Tensor内部的切分操作,以及基于索引或者筛选条件的数据选择操作。
|
|||
|
|
|
|||
|
|
当然了,在使用这些函数的时候,你最需要关注的就是边界的数值大小,具体来说就是维度和大小相关的参数,一定要提前仔细计算好,要不然就会产生错误的结果。
|
|||
|
|
|
|||
|
|
结合众多的例子,我相信你一定可以拿下这些操作。
|
|||
|
|
|
|||
|
|
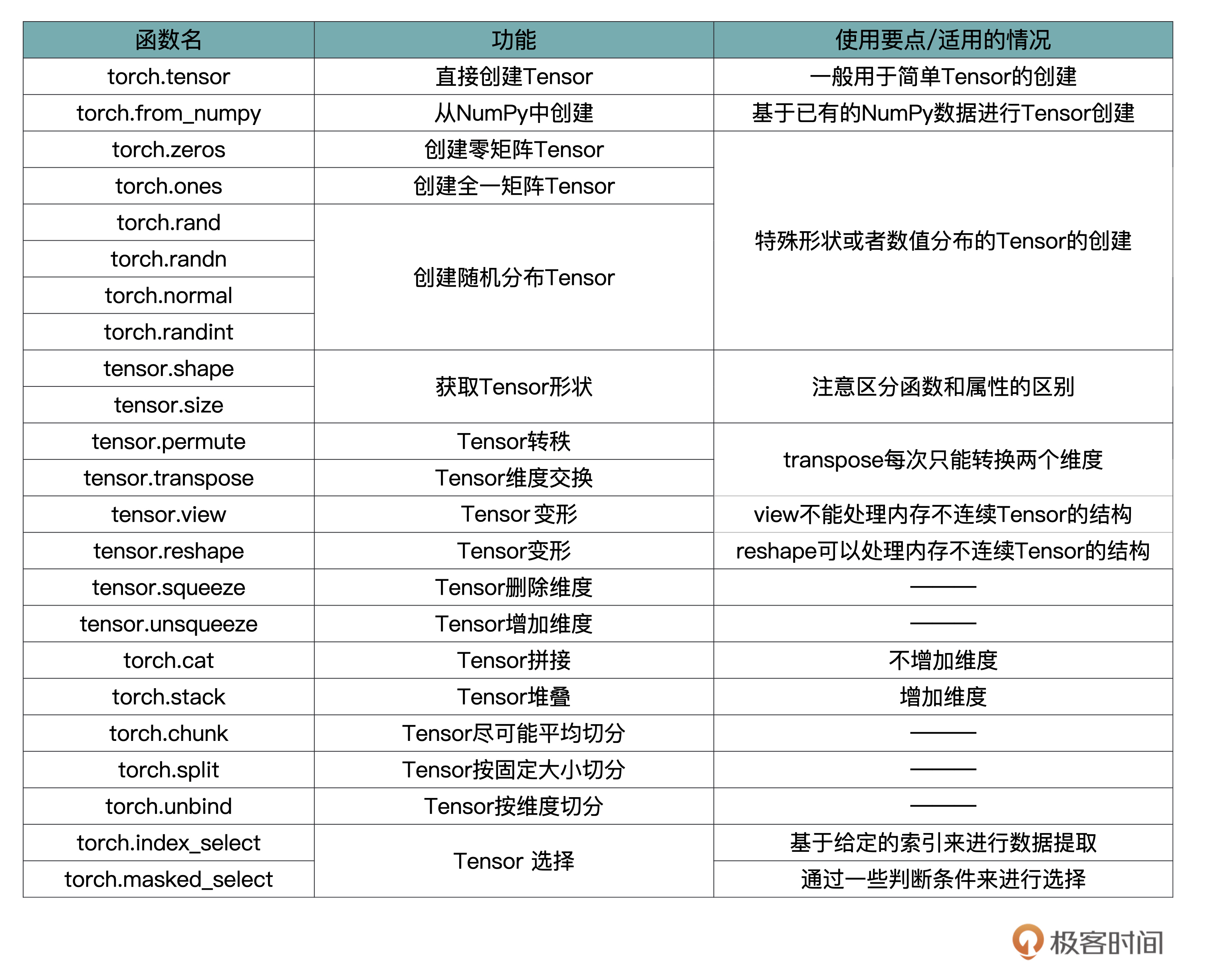
这里我特意给你梳理了一张表格,总结归纳了Tensor中的主要函数跟用法。不过这些参数咱们也不用死记硬背,我们在使用的时候,根据需要灵活查询相关的参数列表即可。
|
|||
|
|
|
|||
|
|
通过这两节课,我们搞懂了Tensor的一系列操作,在以后的项目中,你就可以游刃有余地对Tensor进行各种花式操作了,加油!
|
|||
|
|
|
|||
|
|
## 每课一练
|
|||
|
|
|
|||
|
|
现在有个Tensor,如下:
|
|||
|
|
|
|||
|
|
```python
|
|||
|
|
>>> A=torch.tensor([[4,5,7], [3,9,8],[2,3,4]])
|
|||
|
|
>>> A
|
|||
|
|
tensor([[4, 5, 7],
|
|||
|
|
[3, 9, 8],
|
|||
|
|
[2, 3, 4]])
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
我们想提取出其中第一行的第一个,第二行的第一、第二个,第三行的最后一个,该怎么做呢?
|
|||
|
|
|
|||
|
|
欢迎你在留言区跟我交流互动,也推荐你把这节课分享给更多同事、朋友!
|
|||
|
|
|