463 lines
19 KiB
Markdown
463 lines
19 KiB
Markdown
|
|
# 02 | NumPy(上):核心数据结构详解
|
|||
|
|
|
|||
|
|
你好,我是方远。
|
|||
|
|
|
|||
|
|
通过前面两节课,我们已经对PyTorch有了初步的了解,你是不是迫不及待想要动手玩转PyTorch了?先别着急,我们有必要先品尝一道“前菜”,它就是NumPy。
|
|||
|
|
|
|||
|
|
为什么我们要先拿下NumPy呢?我相信,无论你正在从事或打算入门机器学习,不接触NumPy几乎不可能。现在的主流深度学习框架PyTorch与TensorFlow中最基本的计算单元Tensor,都与NumPy数组有着类似的计算逻辑,可以说掌握了NumPy对学习这两种框架都有很大帮助。
|
|||
|
|
|
|||
|
|
另外,NumPy还被广泛用在Pandas,SciPy等其他数据科学与科学计算的Python模块中。而我们日常用得越来越多的人脸识别技术(属于计算机视觉领域),其原理本质上就是先把图片转换成NumPy的数组,然后再进行一系列处理。
|
|||
|
|
|
|||
|
|
为了让你真正吃透NumPy,我会用两节课的内容讲解NumPy。这节课,我们先介绍NumPy的数组、数组的关键属性以及非常重要的轴的概念。
|
|||
|
|
|
|||
|
|
## 什么是NumPy
|
|||
|
|
|
|||
|
|
NumPy是用于Python中科学计算的一个基础包。它提供了一个多维度的数组对象(稍后展开),以及针对数组对象的各种快速操作,例如排序、变换,选择等。NumPy的安装方式非常简单,可以使用Conda安装,命令如下:
|
|||
|
|
|
|||
|
|
```plain
|
|||
|
|
conda install numpy
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
或使用pip进行安装,命令如下:
|
|||
|
|
|
|||
|
|
```plain
|
|||
|
|
pip install numpy
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
## NumPy数组
|
|||
|
|
|
|||
|
|
刚才所说的数组对象是NumPy中最核心的组成部分,这个数组叫做ndarray,是“N-dimensional array”的缩写。其中的N是一个数字,指代维度,例如你常常能听到的1-D数组、2-D数组或者更高维度的数组。
|
|||
|
|
|
|||
|
|
在NumPy中,数组是由numpy.ndarray 类来实现的,它是NumPy的核心数据结构。我们今天的内容就是围绕它进行展开的。
|
|||
|
|
|
|||
|
|
学习一个新知识,我们常用的方法就是跟熟悉的东西做对比。NumPy数组从逻辑上来看,与其他编程语言中的数组是一样的,索引也是从0开始。而Python中的列表,其实也可以达到与NumPy数组相同的功能,但它们又有差异,做个对比你就能体会到NumPy数组的特点了。
|
|||
|
|
|
|||
|
|
1.Python中的列表可以动态地改变,而NumPy数组是不可以的,它在创建时就有固定大小了。改变Numpy数组长度的话,会新创建一个新的数组并且删除原数组。
|
|||
|
|
2.NumPy数组中的数据类型必须是一样的,而列表中的元素可以是多样的。
|
|||
|
|
3.NumPy针对NumPy数组一系列的运算进行了优化,使得其速度特别快,并且相对于Python中的列表,同等操作只需使用更少的内存。
|
|||
|
|
|
|||
|
|
## 创建数组
|
|||
|
|
|
|||
|
|
好,那就让我们来看看NumPy数组是怎么创建的吧?
|
|||
|
|
|
|||
|
|
最简单的方法就是把一个列表传入到np.array()或np.asarray()中,这个列表可以是任意维度的。np.array()属于深拷贝,np.asarray()则是浅拷贝,它们的区别我们下节课再细讲,这里你有个印象就行。
|
|||
|
|
|
|||
|
|
我们可以先试着创建一个一维的数组,代码如下。
|
|||
|
|
|
|||
|
|
```plain
|
|||
|
|
>>>import numpy as np
|
|||
|
|
>>>#引入一次即可
|
|||
|
|
|
|||
|
|
>>>arr_1_d = np.asarray([1])
|
|||
|
|
>>>print(arr_1_d)
|
|||
|
|
[1]
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
再创建一个二维数组:
|
|||
|
|
|
|||
|
|
```plain
|
|||
|
|
>>>arr_2_d = np.asarray([[1, 2], [3, 4]])
|
|||
|
|
>>>print(arr_2_d)
|
|||
|
|
[[1 2]
|
|||
|
|
[3 4]]
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
你也可以试试自己创建更高维度的数组。
|
|||
|
|
|
|||
|
|
### 数组的属性
|
|||
|
|
|
|||
|
|
作为一个数组,NumPy有一些固有的属性,我们今天来介绍非常常用且关键的数组维度、形状、size与数据类型。
|
|||
|
|
|
|||
|
|
#### ndim
|
|||
|
|
|
|||
|
|
ndim表示数组维度(或轴)的个数。刚才创建的数组arr\_1\_d的轴的个数就是1,arr\_2\_d的轴的个数就是2。
|
|||
|
|
|
|||
|
|
```plain
|
|||
|
|
>>>arr_1_d.ndim
|
|||
|
|
1
|
|||
|
|
>>>arr_2_d.ndim
|
|||
|
|
2
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
#### shape
|
|||
|
|
|
|||
|
|
shape表示数组的维度或形状, 是一个整数的元组,元组的长度等于ndim。
|
|||
|
|
|
|||
|
|
arr\_1\_d的形状就是(1,)(一个向量), arr\_2\_d的形状就是(2, 2)(一个矩阵)。
|
|||
|
|
|
|||
|
|
```plain
|
|||
|
|
>>>arr_1_d.shape
|
|||
|
|
(1,)
|
|||
|
|
>>>arr_2_d.shape
|
|||
|
|
(2, 2)
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
shape这个属性在实际中用途还是非常广的。比如说,我们现在有这样的数据(B, W, H, C),熟悉深度学习的同学肯定会知道,这代表一个batch size 为B的(W,H,C)数据。
|
|||
|
|
|
|||
|
|
现在我们需要根据(W,H,C)对数据进行变形或者其他处理,这时我们可以直接使用input\_data.shape\[1:3\]获取到数据的形状,而不需要直接在程序中硬编程、直接写好输入数据的宽高以及通道数。
|
|||
|
|
|
|||
|
|
在实际的工作当中,我们经常需要对数组的形状进行变换,就可以使用arr.reshape()函数,在不改变数组元素内容的情况下变换数组的形状。但是你需要注意的是,**变换前与变换后数组的元素个数需要是一样的**,请看下面的代码。
|
|||
|
|
|
|||
|
|
```plain
|
|||
|
|
>>>arr_2_d.shape
|
|||
|
|
(2, 2)
|
|||
|
|
>>>arr_2_d
|
|||
|
|
[[1 2]
|
|||
|
|
[3 4]]
|
|||
|
|
# 将arr_2_d reshape为(4,1)的数组
|
|||
|
|
>>>arr_2_d.reshape((4,1))
|
|||
|
|
array([[1],
|
|||
|
|
[2],
|
|||
|
|
[3],
|
|||
|
|
[4]])
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
我们还可以使用np.reshape(a, newshape, order)对数组a进行reshape,新的形状在newshape中指定。
|
|||
|
|
|
|||
|
|
这里需要注意的是,reshape函数有个**order参数**,它是指以什么样的顺序读写元素,其中有这样几个参数。
|
|||
|
|
|
|||
|
|
* ‘C’:默认参数,使用类似C-like语言(行优先)中的索引方式进行读写。
|
|||
|
|
* ‘F’:使用类似Fortran-like语言(列优先)中的索引方式进行读写。
|
|||
|
|
* ‘A’:原数组如果是按照‘C’的方式存储数组,则用‘C’的索引对数组进行reshape,否则使用’F’的索引方式。
|
|||
|
|
|
|||
|
|
reshape的过程你可以这样理解,首先需要根据指定的方式(‘C’或’F’)将原数组展开,然后再根据指定的方式写入到新的数组中。
|
|||
|
|
|
|||
|
|
这是什么意思呢?先看一个简单的2维数组的例子。
|
|||
|
|
|
|||
|
|
```plain
|
|||
|
|
>>>a = np.arange(6).reshape(2,3)
|
|||
|
|
array([[0, 1, 2],
|
|||
|
|
[3, 4, 5]])
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
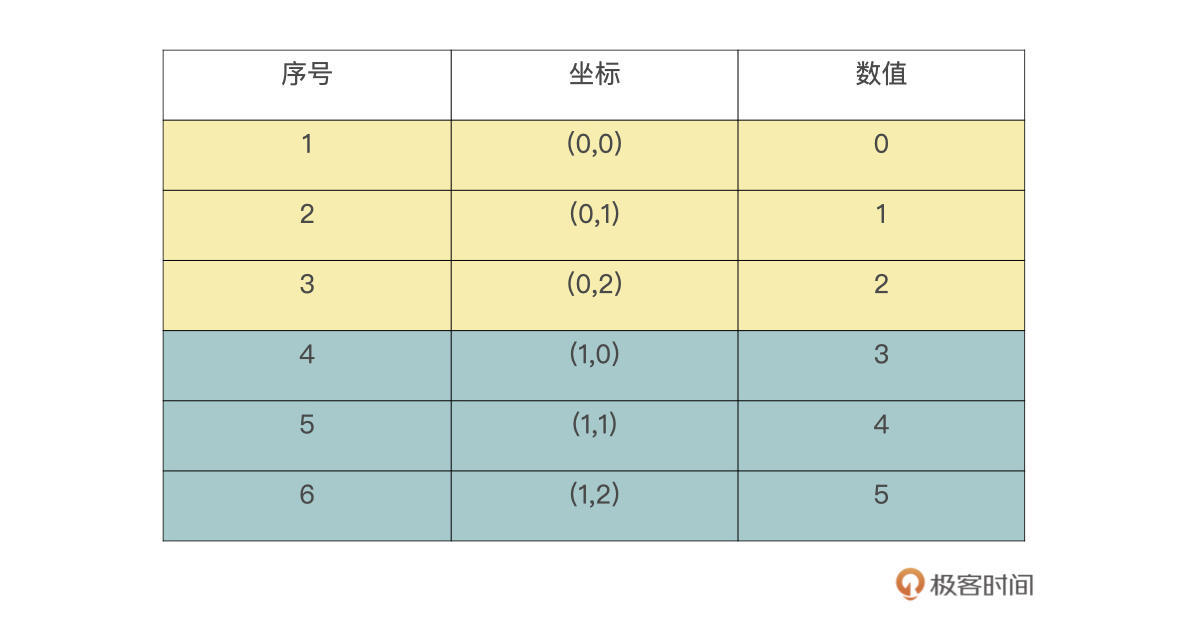
我们要将数组a,按照’C’的方式reshape成(3,2),可以这样操作。首先将原数组展开,对于‘C’的方式来说是行优先,最后一个维度最优先改变,所以展开结果如下,序号那一列代表展开顺序。
|
|||
|
|
|
|||
|
|
|
|||
|
|
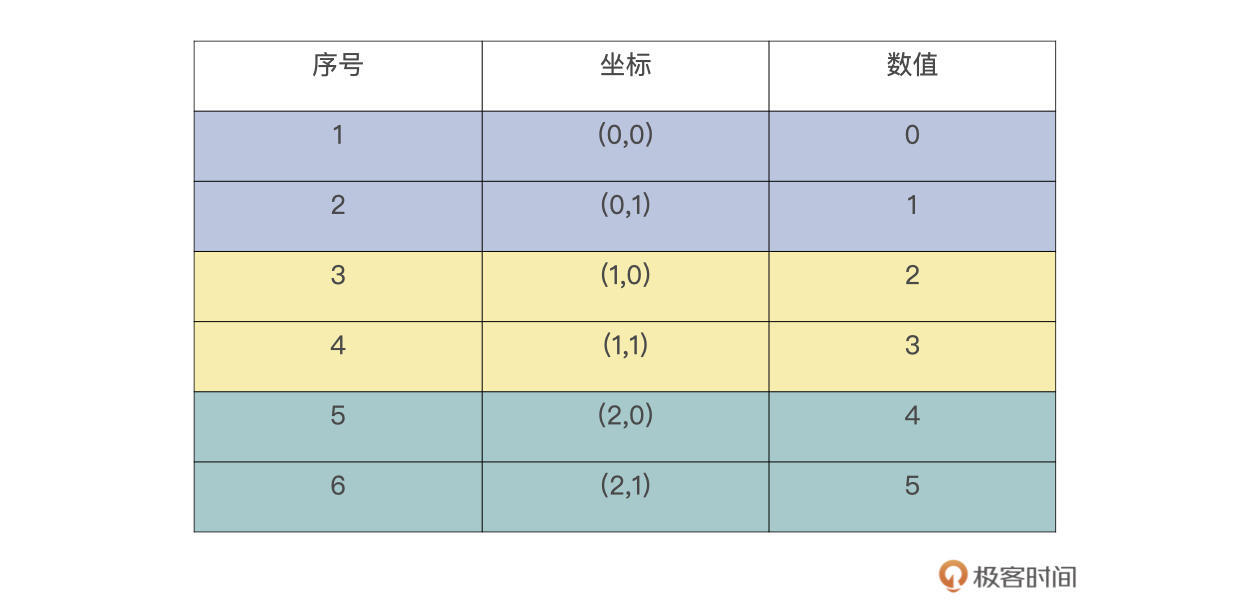
所以,reshape后的数组,是按照0,1,2,3,4,5这个序列进行写入数据的。reshape后的数组如下表所示,序号代表写入顺序。
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
接下来,再看看将数组a,按照’F’的方式reshape成(3,2)要如何处理。
|
|||
|
|
|
|||
|
|
对于行优先的方式,我们应该是比较熟悉的,而‘F’方式是列优先的方式,这一点对于没有使用过列优先的同学来说,可能比较难理解一点。
|
|||
|
|
|
|||
|
|
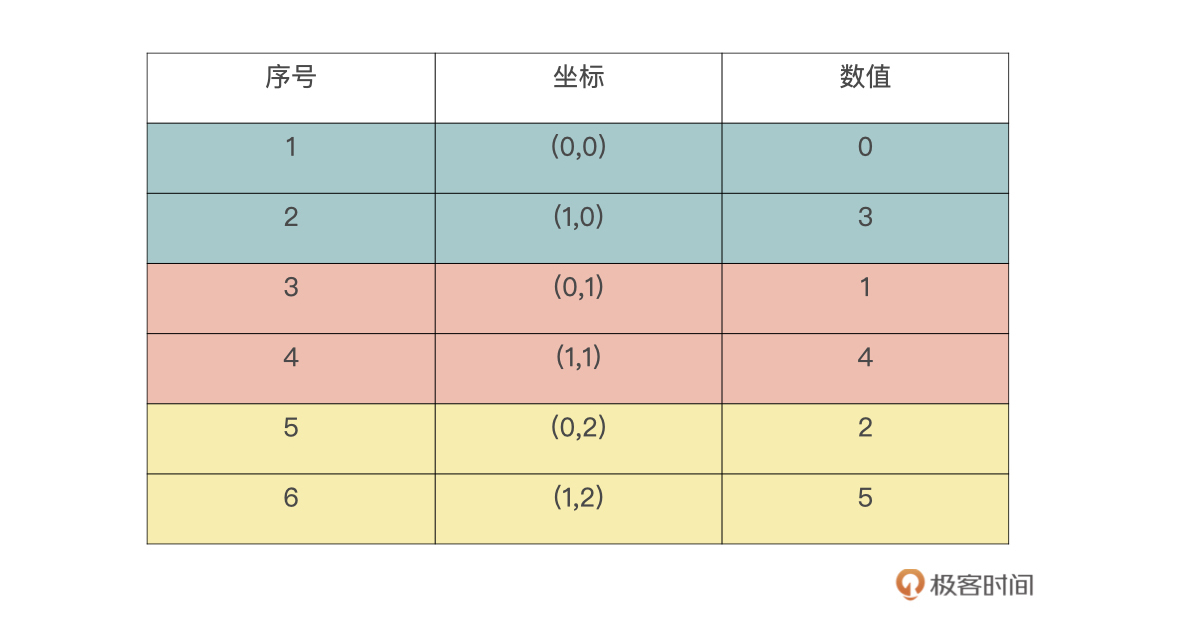
首先是按列优先展开原数组,列优先意味着最先变化的是数组的第一个维度。下表是展开后的结果,序号是展开顺序,这里请注意下**坐标的变换方式**(第一个维度最先变化)。
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
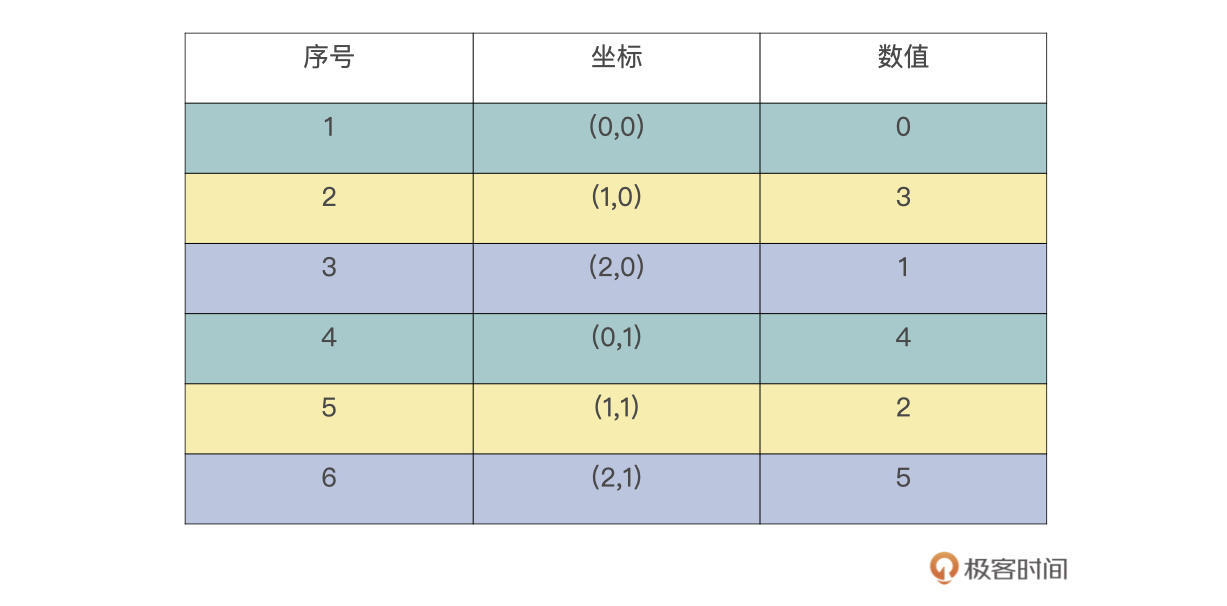
所以,reshape后的数组,是按照0,3,1,4,2,5这个序列进行写入数据的。reshape后的数组如下表所示,序号代表写入顺序,为了显示直观,我将相同行以同样颜色显示了。
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
这里我给你留一个小练习,你可以试试对多维数组的reshape吗?
|
|||
|
|
|
|||
|
|
不过,大部分时候还是使用’C’的方式比较多,也就是行优先的形式。至少目前为止我还没有使用过’F’与’A’的方式。
|
|||
|
|
|
|||
|
|
#### size
|
|||
|
|
|
|||
|
|
size,也就是数组元素的总数,它就等于shape属性中元素的乘积。
|
|||
|
|
|
|||
|
|
请看下面的代码,arr\_2\_d的size是4。
|
|||
|
|
|
|||
|
|
```plain
|
|||
|
|
>>>arr_2_d.size
|
|||
|
|
4
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
#### dtype
|
|||
|
|
|
|||
|
|
最后要说的是dtype,它是一个描述数组中元素类型的对象。使用dtype属性可以查看数组所属的数据类型。
|
|||
|
|
|
|||
|
|
NumPy中大部分常见的数据类型都是支持的,例如int8、int16、int32、float32、float64等。dtype是一个常见的属性,在创建数组,数据类型转换时都可以看到它。
|
|||
|
|
|
|||
|
|
首先我们看看arr\_2\_d的数据类型:
|
|||
|
|
|
|||
|
|
```plain
|
|||
|
|
>>>arr_2_d.dtype
|
|||
|
|
dtype('int64')
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
你可以回头看一下刚才创建arr\_2\_d的时候,我们并没有指定数据类型,如果没有指定数据类型,NumPy会自动进行判断,然后给一个默认的数据类型。
|
|||
|
|
|
|||
|
|
我们再看下面的代码,我们在创建arr\_2\_d时,对数据类型进行了指定。
|
|||
|
|
|
|||
|
|
```plain
|
|||
|
|
>>>arr_2_d = np.asarray([[1, 2], [3, 4]], dtype='float')
|
|||
|
|
>>>arr_2_d.dtype
|
|||
|
|
dtype('float64')
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
数组的数据类型当然也可以改变,我们可以使用astype()改变数组的数据类型,不过改变数据类型会创建一个新的数组,而不是改变原数组的数据类型。
|
|||
|
|
|
|||
|
|
请看后面的代码。
|
|||
|
|
|
|||
|
|
```plain
|
|||
|
|
>>>arr_2_d.dtype
|
|||
|
|
dtype('float64')
|
|||
|
|
>>>arr_2_d.astype('int32')
|
|||
|
|
array([[1, 2],
|
|||
|
|
[3, 4]], dtype=int32)
|
|||
|
|
>>>arr_2_d.dtype
|
|||
|
|
dtype('float64')
|
|||
|
|
# 原数组的数据类型并没有改变
|
|||
|
|
>>>arr_2_d_int = arr_2_d.astype('int32')
|
|||
|
|
>>>arr_2_d_int.dtype
|
|||
|
|
dtype('int32')
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
但是,我想提醒你,**不能通过直接修改数据类型来修改数组的数据类型**,这样代码虽然不会报错,但是数据会发生改变,请看下面的代码:
|
|||
|
|
|
|||
|
|
```plain
|
|||
|
|
>>>arr_2_d.dtype
|
|||
|
|
dtype('float64')
|
|||
|
|
>>>arr_2_d.size
|
|||
|
|
4
|
|||
|
|
>>>arr_2_d.dtype='int32'
|
|||
|
|
>>>arr_2_d
|
|||
|
|
array([[ 0, 1072693248, 0, 1073741824],
|
|||
|
|
[ 0, 1074266112, 0, 1074790400]], dtype=int32)
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
1个float64相当于2个int32,所以原有的4个float32,会变为8个int32,然后直接输出这个8个int32。
|
|||
|
|
|
|||
|
|
### 其他创建数组的方式
|
|||
|
|
|
|||
|
|
除了使用np.asarray或np.array来创建一个数组之外,NumPy还提供了一些按照既定方式来创建数组的方法,我们只需按照要求,提供一些必要的参数即可。
|
|||
|
|
|
|||
|
|
#### np.ones() 与np.zeros()
|
|||
|
|
|
|||
|
|
np.ones()用来创建一个全1的数组,必须参数是指定数组的形状,可选参数是数组的数据类型,你可以结合下面的代码进行理解。
|
|||
|
|
|
|||
|
|
```plain
|
|||
|
|
>>>np.ones()
|
|||
|
|
Traceback (most recent call last):
|
|||
|
|
File "<stdin>", line 1, in <module>
|
|||
|
|
TypeError: ones() takes at least 1 argument (0 given)
|
|||
|
|
# 报错原因是没有给定形状的参数
|
|||
|
|
>>>np.ones(shape=(2,3))
|
|||
|
|
array([[1., 1., 1.],
|
|||
|
|
[1., 1., 1.]])
|
|||
|
|
>>>np.ones(shape=(2,3), dtype='int32')
|
|||
|
|
array([[1, 1, 1],
|
|||
|
|
[1, 1, 1]], dtype=int32)
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
创建全0的数组是np.zeros(),用法与np.ones()类似,我们就不举例了。
|
|||
|
|
|
|||
|
|
那这两个函数一般什么时候用呢?例如,如果需要初始化一些权重的时候就可以用上,比如说生成一个2x3维的数组,每个数值都是0.5,可以这样做。
|
|||
|
|
|
|||
|
|
```plain
|
|||
|
|
>>>np.ones((2, 3)) * 0.5
|
|||
|
|
array([[0.5, 0.5, 0.5],
|
|||
|
|
[0.5, 0.5, 0.5]]
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
#### np.arange()
|
|||
|
|
|
|||
|
|
我们还可以使用np.arange(\[start, \]stop, \[step, \]dtype=None)创建一个在\[start, stop)区间的数组,元素之间的跨度是step。
|
|||
|
|
|
|||
|
|
start是可选参数,默认为0。stop是必须参数,区间的终点,请注意,刚才说的区间是一个**左闭右开区间**,所以数组并不包含stop。step是可选参数,默认是1。
|
|||
|
|
|
|||
|
|
```plain
|
|||
|
|
# 创建从0到4的数组
|
|||
|
|
>>>np.arange(5)
|
|||
|
|
array([0, 1, 2, 3, 4])
|
|||
|
|
# 从2开始到4的数组
|
|||
|
|
>>>np.arange(2, 5)
|
|||
|
|
array([2, 3, 4])
|
|||
|
|
# 从2开始,到8的数组,跨度是3
|
|||
|
|
>>>np.arange(2, 9, 3)
|
|||
|
|
array([2, 5, 8])
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
#### np.linspace()
|
|||
|
|
|
|||
|
|
最后,我们也可以用np.linspace(start, stop, num=50, endpoint=True, retstep=False, dtype=None)创建一个数组,具体就是创建一个从开始数值到结束数值的等差数列。
|
|||
|
|
|
|||
|
|
* start:必须参数,序列的起始值。
|
|||
|
|
* stop:必须参数,序列的终点。
|
|||
|
|
* num:序列中元素的个数,默认是50。
|
|||
|
|
* endpoint:默认为True,如果为True,则数组最后一个元素是stop。
|
|||
|
|
* retstep:默认为False,如果为True,则返回数组与公差。
|
|||
|
|
|
|||
|
|
```plain
|
|||
|
|
# 从2到10,有3个元素的等差数列
|
|||
|
|
>>>np.linspace(start=2, stop=10, num=3)
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
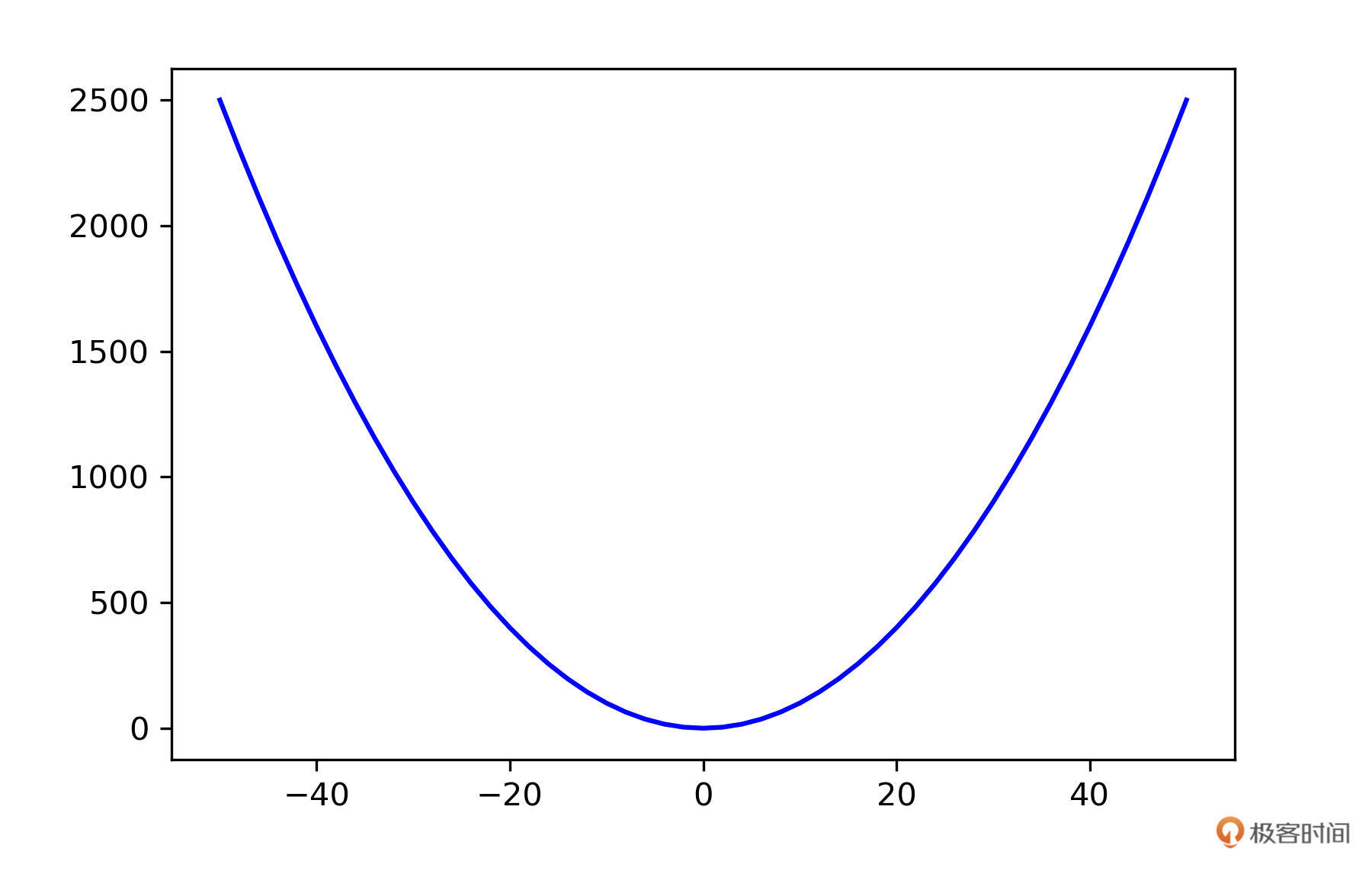
np.arange与np.linspace也是比较常见的函数,比如你要作图的时候,可以用它们生成x轴的坐标。例如,我要生成一个$y=x^{2}$的图片,x轴可以用np.linespace()来生成。
|
|||
|
|
|
|||
|
|
```plain
|
|||
|
|
import numpy as np
|
|||
|
|
import matplotlib.pyplot as plt
|
|||
|
|
|
|||
|
|
X = np.arange(-50, 51, 2)
|
|||
|
|
Y = X ** 2
|
|||
|
|
|
|||
|
|
plt.plot(X, Y, color='blue')
|
|||
|
|
plt.legend()
|
|||
|
|
plt.show()
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
## 数组的轴
|
|||
|
|
|
|||
|
|
这是一个非常重要的概念,也是NumPy数组中最不好理解的一个概念。它经常出现在np.sum()、np.max()这样关键的聚合函数中。
|
|||
|
|
|
|||
|
|
我们用这样一个问题引出,同一个函数如何根据轴的不同来获得不同的计算结果呢?比如现在有一个(4,3)的矩阵,存放着4名同学关于3款游戏的评分数据。
|
|||
|
|
|
|||
|
|
```plain
|
|||
|
|
>>>interest_score = np.random.randint(10, size=(4, 3))
|
|||
|
|
>>>interest_score
|
|||
|
|
array([[4, 7, 5],
|
|||
|
|
[4, 2, 5],
|
|||
|
|
[7, 2, 4],
|
|||
|
|
[1, 2, 4]])
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
第一个需求是,计算每一款游戏的评分总和。这个问题如何解决呢,我们一起分析一下。
|
|||
|
|
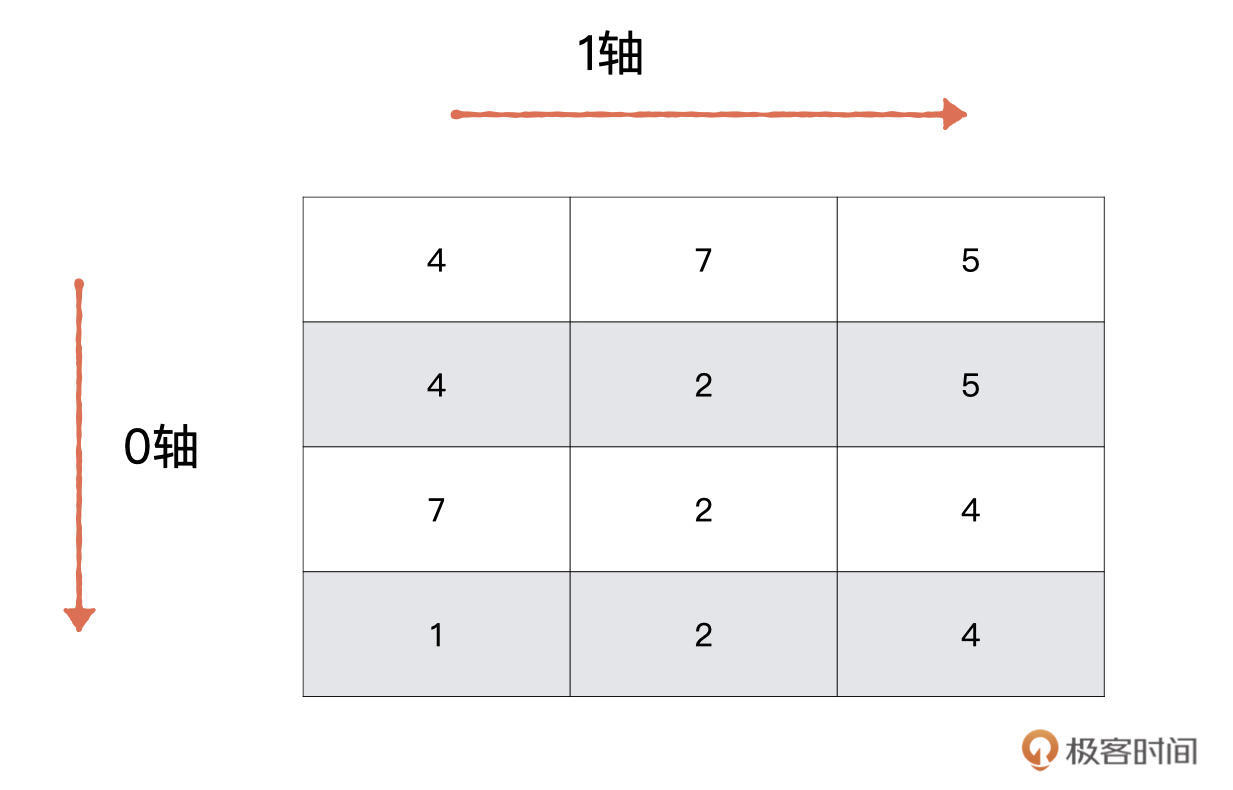
数组的轴即数组的维度,它是从0开始的。对于我们这个二维数组来说,有两个轴,分别是代表行的0轴与代表列的1轴。如下图所示。
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
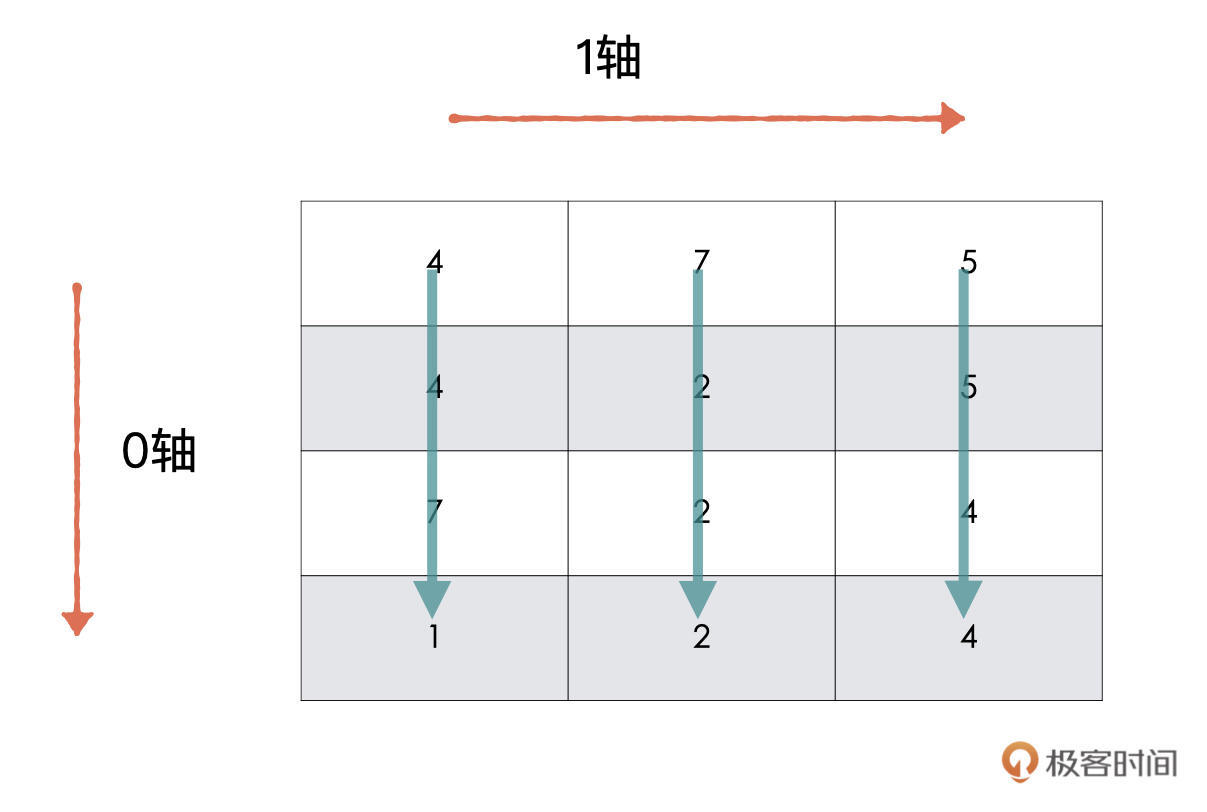
我们的问题是要计算每一款游戏的评分总和,也就是沿着0轴的方向进行求和。所以,我们只需要在求和函数中指定沿着0轴的方向求和即可。
|
|||
|
|
|
|||
|
|
```plain
|
|||
|
|
>>> np.sum(interest_score, axis=0)
|
|||
|
|
array([16, 13, 18])
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
计算方向如绿色箭头所示:
|
|||
|
|
|
|||
|
|
|
|||
|
|
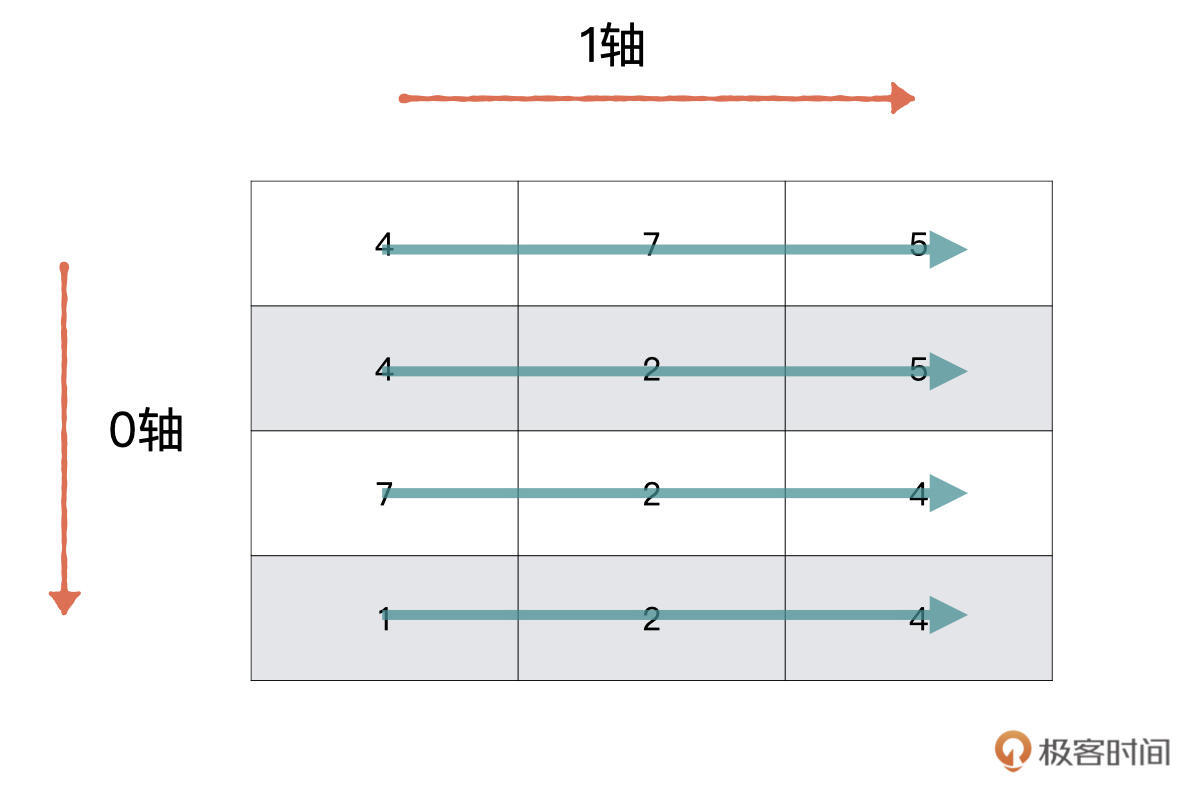
第二个问题是要计算每名同学的评分总和,也就是要沿着1轴方向对二维数组进行操作。所以,我们只需要将axis参数设定为1即可。
|
|||
|
|
|
|||
|
|
```plain
|
|||
|
|
>>> np.sum(interest_score, axis=1)
|
|||
|
|
array([16, 11, 13, 7])
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
计算方向如绿色箭头所示。
|
|||
|
|
|
|||
|
|
|
|||
|
|
二维数组还是比较好理解的,那多维数据该怎么办呢?你有没有发现,其实当axis=i时,就是按照第i个轴的方向进行计算的,或者可以理解为第i个轴的数据将会被折叠或聚合到一起。
|
|||
|
|
|
|||
|
|
形状为(a, b, c)的数组,沿着0轴聚合后,形状变为(b, c);沿着1轴聚合后,形状变为(a, c);
|
|||
|
|
|
|||
|
|
沿着2轴聚合后,形状变为(a, b);更高维数组以此类推。
|
|||
|
|
|
|||
|
|
接下来,我们再看一个多维数组的例子。对数组a,求不同维度上的最大值。
|
|||
|
|
|
|||
|
|
```plain
|
|||
|
|
>>> a = np.arange(18).reshape(3,2,3)
|
|||
|
|
>>> a
|
|||
|
|
array([[[ 0, 1, 2],
|
|||
|
|
[ 3, 4, 5]],
|
|||
|
|
|
|||
|
|
[[ 6, 7, 8],
|
|||
|
|
[ 9, 10, 11]],
|
|||
|
|
|
|||
|
|
[[12, 13, 14],
|
|||
|
|
[15, 16, 17]]])
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
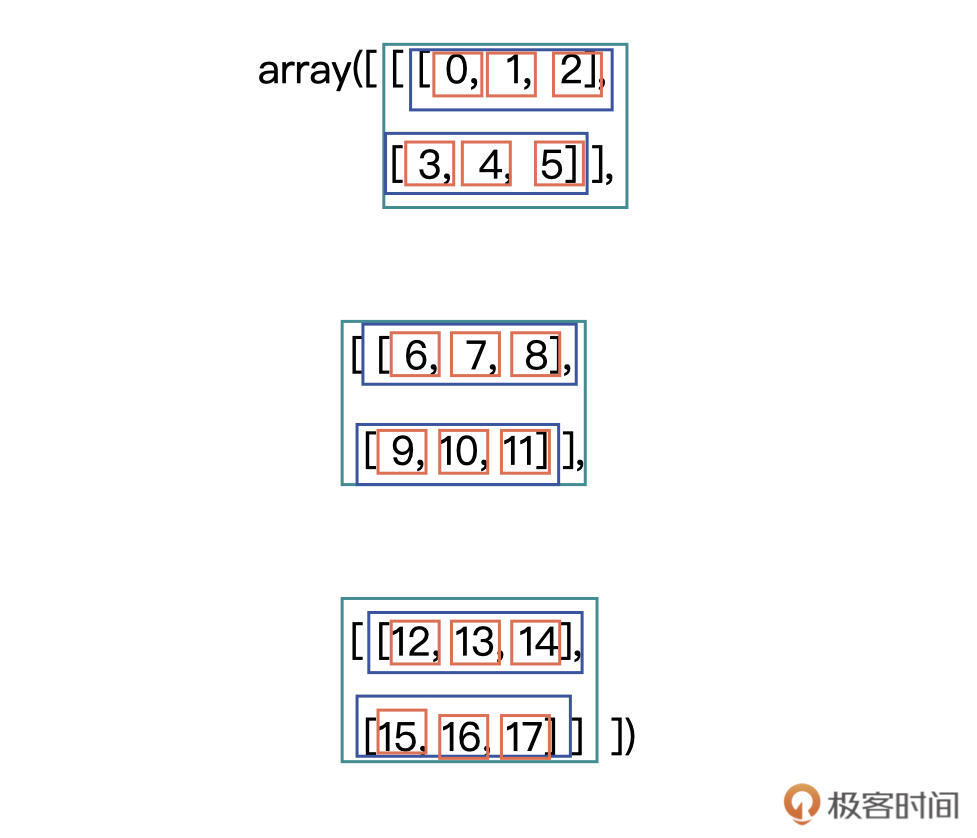
我们可以将同一个轴上的数据看做同一个单位,那聚合的时候,我们只需要在同级别的单位上进行聚合就可以了。
|
|||
|
|
如下图所示,绿框代表沿着0轴方向的单位,蓝框代表着沿着1轴方向的单位,红框代表着2轴方向的单位。
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
当axis=0时,就意味着将三个绿框的数据聚合在一起,结果是一个(2,3)的数组,数组内容为:$$\\begin{matrix}
|
|||
|
|
\[ \\ \[(max(a\_{000},a\_{100},a\_{200}), max(a\_{001},a\_{101},a\_{201}), max(a\_{002},a\_{102},a\_{202}))\], \\\\\\
|
|||
|
|
\[(max(a\_{010},a\_{110},a\_{210}), max(a\_{011},a\_{111},a\_{211}), max(a\_{012},a\_{112},a\_{212}))\] \\ \] \\
|
|||
|
|
\\end{matrix}$$
|
|||
|
|
|
|||
|
|
代码如下:
|
|||
|
|
|
|||
|
|
```plain
|
|||
|
|
>>> a.max(axis=0)
|
|||
|
|
array([[12, 13, 14],
|
|||
|
|
[15, 16, 17]])
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
当axis=1时,就意味着每个绿框内的蓝框聚合在一起,结果是一个(3,3)的数组,数组内容为:
|
|||
|
|
$$\\begin{matrix}
|
|||
|
|
\[ \\ \[(max(a\_{000},a\_{010}), max(a\_{001},a\_{011}), max(a\_{002},a\_{012}))\], \\\\\\
|
|||
|
|
\[(max(a\_{100},a\_{110}), max(a\_{101},a\_{111}), max(a\_{102},a\_{112}))\], \\\\\\
|
|||
|
|
\[(max(a\_{200},a\_{210}), max(a\_{201},a\_{211}), max(a\_{202},a\_{212}))\], \\ \] \\
|
|||
|
|
\\end{matrix}
|
|||
|
|
$$
|
|||
|
|
|
|||
|
|
代码如下:
|
|||
|
|
|
|||
|
|
```plain
|
|||
|
|
>>> a.max(axis=1)
|
|||
|
|
array([[ 3, 4, 5],
|
|||
|
|
[ 9, 10, 11],
|
|||
|
|
[15, 16, 17]])
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
当axis=2时,就意味着每个蓝框中的红框聚合在一起,结果是一个(3,2)的数组,数组内容如下所示:
|
|||
|
|
$$\\begin{matrix}
|
|||
|
|
\[ \\ \[(max(a\_{000},a\_{001},a\_{002}), max(a\_{010},a\_{011},a\_{012}))\], \\\\\\
|
|||
|
|
\[(max(a\_{100},a\_{101},a\_{102}), max(a\_{110},a\_{111},a\_{112}))\], \\\\\\
|
|||
|
|
\[(max(a\_{200},a\_{201},a\_{202}), max(a\_{210},a\_{211},a\_{212}))\], \\ \] \\\\\\
|
|||
|
|
\\end{matrix}
|
|||
|
|
$$
|
|||
|
|
|
|||
|
|
代码如下:
|
|||
|
|
|
|||
|
|
```plain
|
|||
|
|
>>> a.max(axis=2)
|
|||
|
|
array([[ 2, 5],
|
|||
|
|
[ 8, 11],
|
|||
|
|
[14, 17]])
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
axis参数非常常见,不光光出现在刚才介绍的sum与max,还有很多其他的聚合函数也会用到,例如min、mean、argmin(求最小值下标)、argmax(求最大值下标)等。
|
|||
|
|
|
|||
|
|
## 小结
|
|||
|
|
|
|||
|
|
恭喜你完成了这节课的学习。其实你只要有一些其他语言的编程基础,学Numpy还是非常容易的。这里我想再次强调一下为什么NumPy这道前菜必不可少。
|
|||
|
|
|
|||
|
|
其实Numpy的很多知识点是与PyTorch融会贯通的,例如PyTorch中的Tensor。而且Numpy在机器学习中常常被用到,很多模块都要基于NumPy展开,尤其是在数据的预处理和膜后处理中。
|
|||
|
|
|
|||
|
|
NumPy是用于Python中科学计算的一个基础包。它提供了一个多维度的数组对象,以及针对数组对象的各种快速操作。为了让你有更直观的体验,我们学习了创建数组的四种方式。
|
|||
|
|
|
|||
|
|
其中你重点要掌握的方法,就是如何使用**np.asarray**创建一个数组。这里涉及数组属性(ndim、shape、dtype、size)的灵活使用,特别是数组的形状变化与数据类型转换。
|
|||
|
|
|
|||
|
|
最后,我为你介绍了数组轴的概念,我们需要在数组的聚合函数中灵活运用它。虽然这个概念十分常用,但却不好理解,建议你根据我课程里的例子仔细揣摩一下,从2维数组一步步推理到多维数组,根据轴的不同,数组聚合的方向是如何变化的。
|
|||
|
|
|
|||
|
|
下一节课,我们要继续学习NumPy中常用且重要的功能。
|
|||
|
|
|
|||
|
|
## 每课一练
|
|||
|
|
|
|||
|
|
在刚才用户对游戏评分的那个问题中,你能计算一下每位用户对三款游戏的打分的平均分吗?
|
|||
|
|
|
|||
|
|
欢迎你在留言区记录你的疑问或者收获,也推荐你把这节课分享给你的朋友。
|
|||
|
|
|