462 lines
26 KiB
Markdown
462 lines
26 KiB
Markdown
|
|
# 05|HashMap:一个优秀的散列表是怎么来的?
|
|||
|
|
|
|||
|
|
你好,我是微扰君。
|
|||
|
|
|
|||
|
|
过去四讲我们学习了STL中全部的序列式容器,数组、链表、队列、栈;今天来谈一谈另一类容器,关联式容器。所谓“关联式”,就是存储数据的时候,不只是存储元素的值本身,同时对要存储的元素关联一个键,形成一组键值对。这样在访问的时候,我们就可以基于键,访问到容器内的元素。
|
|||
|
|
|
|||
|
|
关联式容器本身其实是STL中的概念,其他高级语言中也有类似的概念。我们这次就以JDK为例,讲解几种关联式容器的原理和实现。
|
|||
|
|
|
|||
|
|
## 统计单词次数
|
|||
|
|
|
|||
|
|
我们就从一个实际需求讲起。现在有一篇很长的英文文档,如果希望统计每个单词在文档中出现了多少次,应该怎么做呢?
|
|||
|
|
|
|||
|
|
如果熟悉HashMap的小伙伴一定会很快说出来,我们开一个HashMap,以string类型为key,int类型为value;遍历文档中的每个单词 `word` ,找到键值对中key为 `word` 的项,并对相关的value进行自增操作。如果该key= `word` 的项在 HashMap中不存在,我们就插入一个(word,1)的项表示新增。
|
|||
|
|
|
|||
|
|
这样每组键值对表示的就是某个单词对应的数量,等整个文档遍历完成,我们就可以得到每个单词的数量了。用Java语言实现这个逻辑也不难。
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
import java.util.HashMap;
|
|||
|
|
import java.util.Map;
|
|||
|
|
public class Test {
|
|||
|
|
public static void main(String[] args) {
|
|||
|
|
Map<String, Integer> map = new HashMap<>();
|
|||
|
|
String doc = "aaa bbb ccc aaa bbb ccc ccc bbb ccc ddd";
|
|||
|
|
String[] words = doc.split(" ");
|
|||
|
|
for (String s : words) {
|
|||
|
|
if (!map.containsKey(s)) {
|
|||
|
|
map.put(s, 1);
|
|||
|
|
} else {
|
|||
|
|
map.put(s, map.get(s) + 1);
|
|||
|
|
}
|
|||
|
|
}
|
|||
|
|
System.out.println(map);
|
|||
|
|
}
|
|||
|
|
}
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
**但是HashMap是怎么做到高效统计单词对应数量的?它设计思路的核心究竟是什么呢**?这个问题非常有意思,我们一起来思考一下。
|
|||
|
|
|
|||
|
|
### 一个单词
|
|||
|
|
|
|||
|
|
要统计每个单词的数量有点复杂,如果只统计某一个单词的数量呢,是不是就很好做了?
|
|||
|
|
|
|||
|
|
只需要开一个变量,同样遍历所有单词,遇到和目标单词一样的,才对这个变量进行自增操作;等遍历完成,我们就可以得到该单词的数量了。
|
|||
|
|
|
|||
|
|
按这个思路,一种很简单的想法当然是直接对每一个单词都统计一遍数量,**我们把能想到的所有可能出现的单词都列出来,每个单词,单独用一个变量去统计它出现的数量,遍历所有单词,写一堆if-else来判断当前单词应该被累计到哪个变量中**。
|
|||
|
|
|
|||
|
|
下面的代码是一个例子:
|
|||
|
|
|
|||
|
|
```java
|
|||
|
|
import java.util.HashMap;
|
|||
|
|
import java.util.Map;
|
|||
|
|
public class Main {
|
|||
|
|
public static void main(String[] args) {
|
|||
|
|
int[] cnt = new int[20000];
|
|||
|
|
String doc = "aaa bbb ccc aaa bbb ccc ccc bbb ccc ddd";
|
|||
|
|
String[] words = doc.split(" ");
|
|||
|
|
int aaa = 0;
|
|||
|
|
int bbb = 0;
|
|||
|
|
int ccc = 0;
|
|||
|
|
int ddd = 0;
|
|||
|
|
|
|||
|
|
for (String s : words) {
|
|||
|
|
if (s == "aaa") aaa++;
|
|||
|
|
if (s == "bbb") bbb++;
|
|||
|
|
if (s == "ccc") ccc++;
|
|||
|
|
if (s == "ddd") ddd++;
|
|||
|
|
}
|
|||
|
|
}
|
|||
|
|
}
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
在代码中就对目标文本统计了aaa、bbb、ccc、ddd这四个单词出现的次数。
|
|||
|
|
但这样的代码显然有两个很大的问题:
|
|||
|
|
|
|||
|
|
1. 对单词和计数器的映射关系是通过一堆if-else写死的,维护性很差;
|
|||
|
|
2. 必须已知所有可能出现的单词,如果遇到一个新的单词,就没有办法处理它了。
|
|||
|
|
|
|||
|
|
解决办法有没有呢?这个时候我们不禁想到了老朋友——数组。
|
|||
|
|
|
|||
|
|
我们可以开一个数组去维护计数器。具体做法就是,给每个单词编个号,直接用编号对应下标的数组元素作为它的计数器就好啦。唯一麻烦的地方在于,**如何能把单词对应到一个数字,并且可以不同的单词有不同的编号,且每个单词都可以通过计算或者查找等手段对应到一个唯一的编号上**?
|
|||
|
|
|
|||
|
|

|
|||
|
|
|
|||
|
|
### 解决思路
|
|||
|
|
|
|||
|
|
一种思路就是把文档中出现的字符串,也放在数组里,按照单词出现的顺序对应从0开始连续编号。
|
|||
|
|
|
|||
|
|
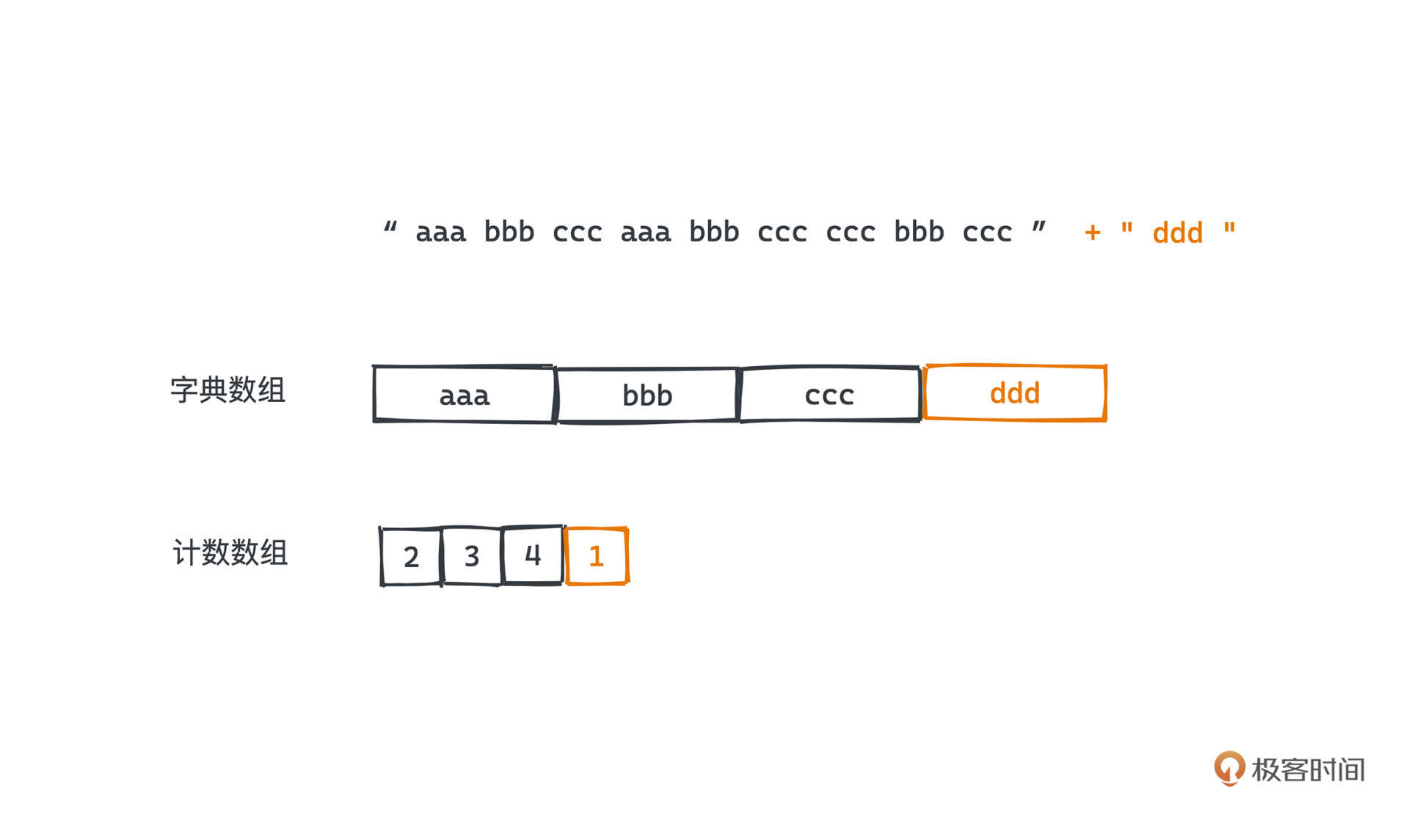
所以,一共要建立两个数组,第一个数组用于存放所有单词,数组下标就是单词编号了,我们称之为字典数组;第二个数组用于存放每个单词对应的计数器,我们称之为计数数组。**这样,单词的下标和计数器的下标是一一对应的**。
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
每遇到一个新的单词,都遍历一遍字典数组,如果没有出现过,我们就将当前单词插入到字典数组结尾。显然,通过遍历字典数组,可以获得当前单词的序号,而有了序号之后,计数数组对应位置的统计计数也非常简单。这样,我们就可以非常方便地对任意文本的任意单词进行计数了,再也不用提前知道文档中有哪些单词了。
|
|||
|
|
|
|||
|
|
至于数组开多大,可以根据英文词典的常用单词数来考虑,相信大部分文档中出现的单词很难超过1w个,那么绝大部分时候,开一个长度为1w的数组肯定就可以满足我们的需求。这样的字典数组,也有人叫做符号表,比如Haskell中的内置map就是基于这个思路实现的。
|
|||
|
|
|
|||
|
|
但很显然,这样的编号方式代价还是非常高,因为基于这么大的数组判断每个单词是否出现过,显然是一个O(D)的操作,其中D代表整个字典空间的大小,也就是一个文档中有多少个不同的单词。整体的时间复杂度是O(D\*N),这并不令人满意。
|
|||
|
|
|
|||
|
|

|
|||
|
|
|
|||
|
|
那这里的本质问题是什么呢?这个问题,其实可以抽象成一个给字符串动态编码的问题,**为了让我们不需要遍历整个符号表来完成指定键的查找操作,我们需要找到一个更高效的给字符串编码的方式**。
|
|||
|
|
|
|||
|
|
### 优化思路
|
|||
|
|
|
|||
|
|
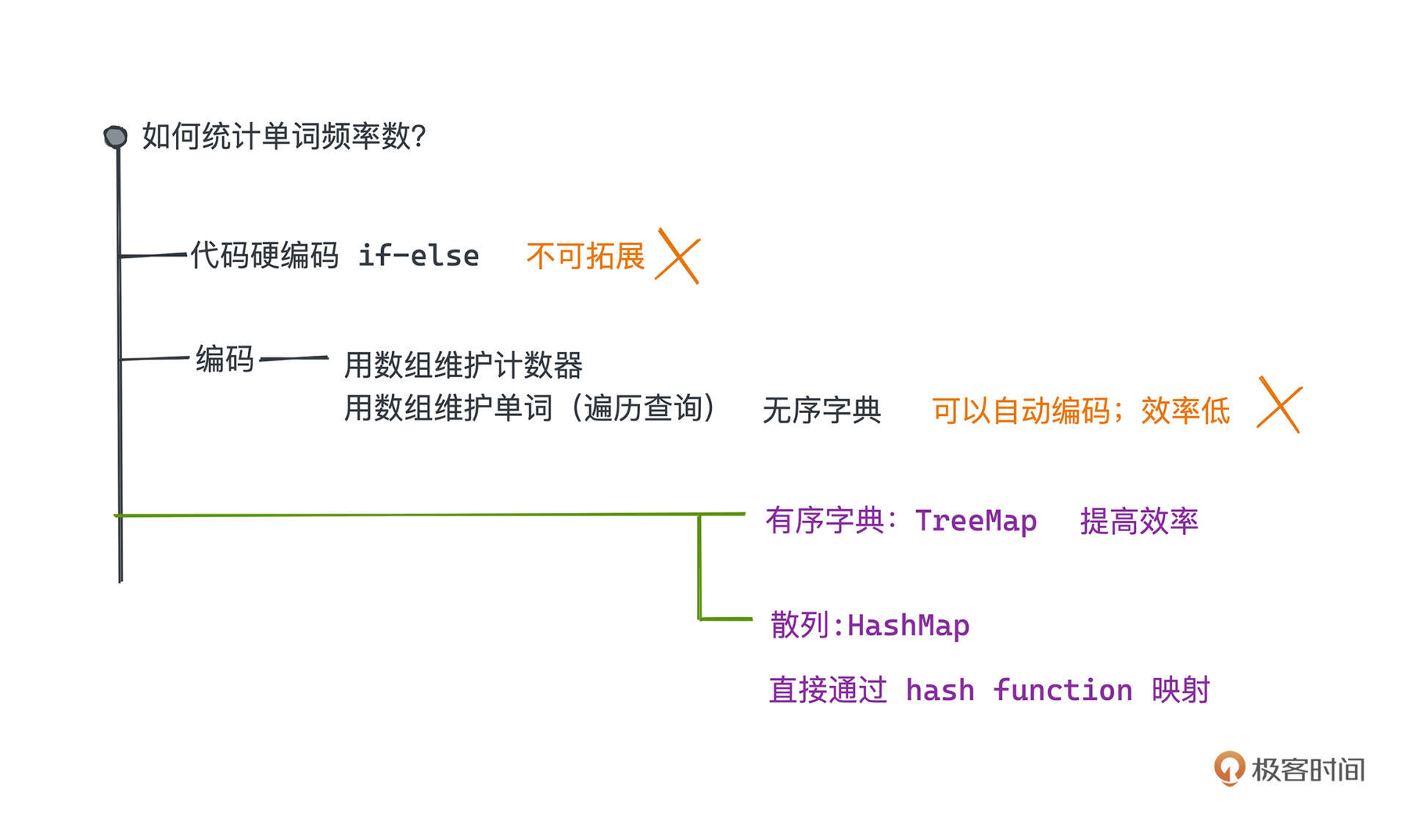
整体的优化方式大概分成两类。
|
|||
|
|
|
|||
|
|
* 一种是我们维护一个有序的数据结构,让比较和插入的过程更加高效,而不是需要遍历每一个元素判断逐一判断,下一讲会介绍的关联式容器TreeMap就是这样实现的。
|
|||
|
|
* 另一种思路就是我们是否能寻找到一种直接基于字符串快速计算出编号的方式,并将这个编号“映射”到一个可以在O(1)时间内基于下标访问的数组中呢?
|
|||
|
|
|
|||
|
|
当然是有的,并且方式很多。
|
|||
|
|
|
|||
|
|
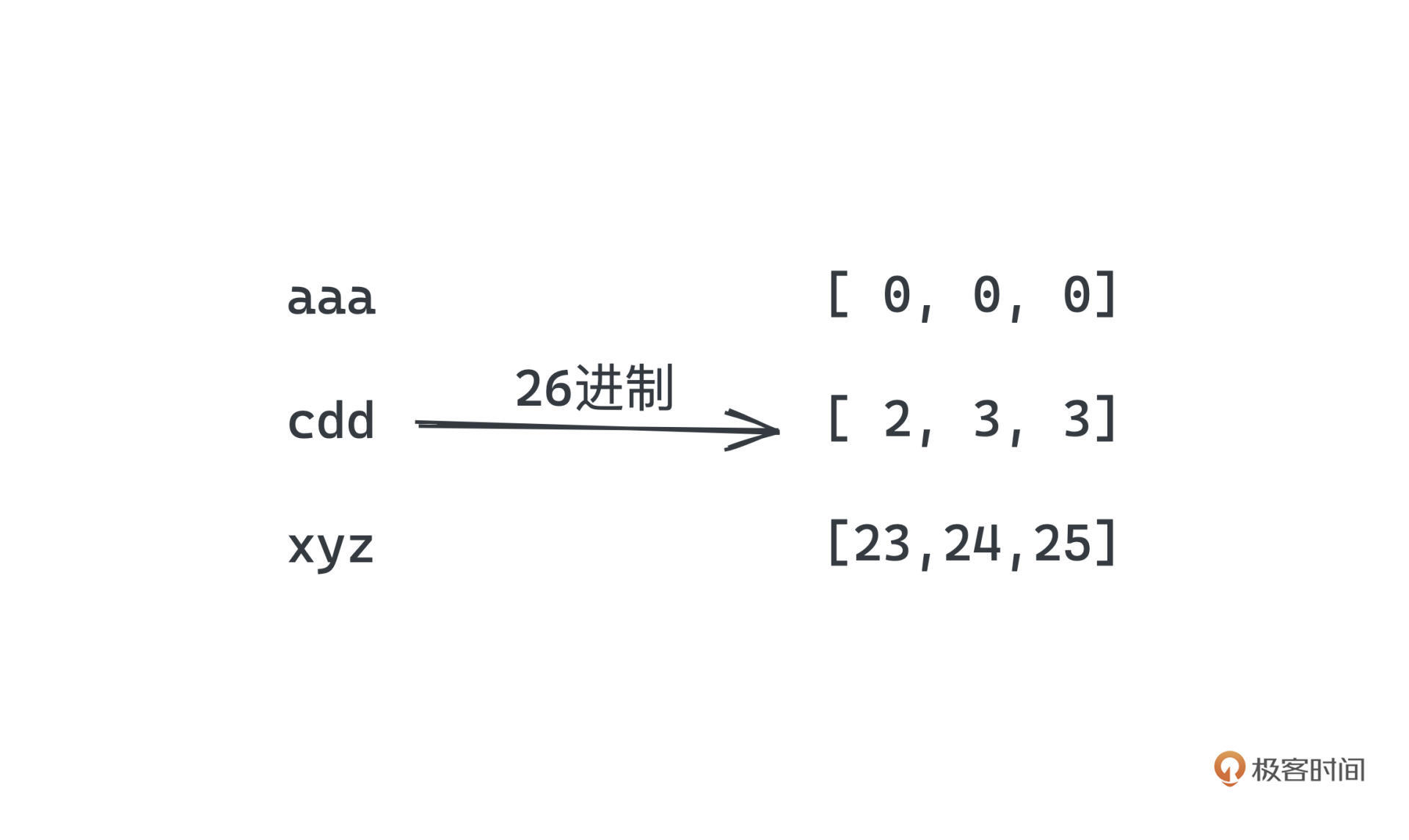
以单词为例,英文单词的每个字母只可能是 a-z,那如果想用数字表示单词,最简单的方式莫过于用26进制来表示这个单词了。具体来说就是,我们用0表示a、1表示b,以此类推,用25表示z,然后将一个单词看成一个26进制的数字即可。
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
基于前面的思路,我们可以开一个比较大的数组来统计每个单词的数量,单词对应的计数器就是计数数组中下标为字符串所对应的二十六进制数的元素。翻译成代码如下:
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
import java.util.HashMap;
|
|||
|
|
import java.util.Map;
|
|||
|
|
public class Main {
|
|||
|
|
public static void main(String[] args) {
|
|||
|
|
|
|||
|
|
int[] cnt = new int[20000];
|
|||
|
|
String doc = "aaa bbb ccc aaa bbb ccc ccc bbb ccc ddd";
|
|||
|
|
String[] words = doc.split(" ");
|
|||
|
|
for (String s : words) {
|
|||
|
|
int tmp = 0;
|
|||
|
|
for (char c: s.toCharArray()) {
|
|||
|
|
tmp *= 26;
|
|||
|
|
tmp += (c - 'a');
|
|||
|
|
}
|
|||
|
|
cnt[tmp]++;
|
|||
|
|
}
|
|||
|
|
String target = "aaa";
|
|||
|
|
int hash = 0;
|
|||
|
|
for (char c: target.toCharArray()) {
|
|||
|
|
hash *= 26;
|
|||
|
|
hash += c - 'a';
|
|||
|
|
}
|
|||
|
|
System.out.println(cnt[hash]);
|
|||
|
|
}
|
|||
|
|
}
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
这样,我们就得到了统计单词数的非常优秀的时间复杂度了,在近似认为单词26进制计算复杂度为O(1)的前提下,我们统计N个单词出现数量的时候,整体甚至只需要O(N)的复杂度,相比于原来的需要遍历字典O(D\*N)的做法就明显高效的多。
|
|||
|
|
|
|||
|
|
这其实就是散列的思想。
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
### 散列
|
|||
|
|
|
|||
|
|
在散列表中,我们所做的也就是为每一个key找到一种类似于上述26进制的函数,使得key可以映射到一个数字中,这样就可以利用数组基于下标随机访问的高效性,迅速在散列表中找到所关联的键值对。
|
|||
|
|
|
|||
|
|
所以散列函数的本质,就是**将一个更大且可能不连续空间(比如所有的单词),映射到一个空间有限的数组里,从而借用数组基于下标O(1)快速随机访问数组元素的能力**。
|
|||
|
|
|
|||
|
|
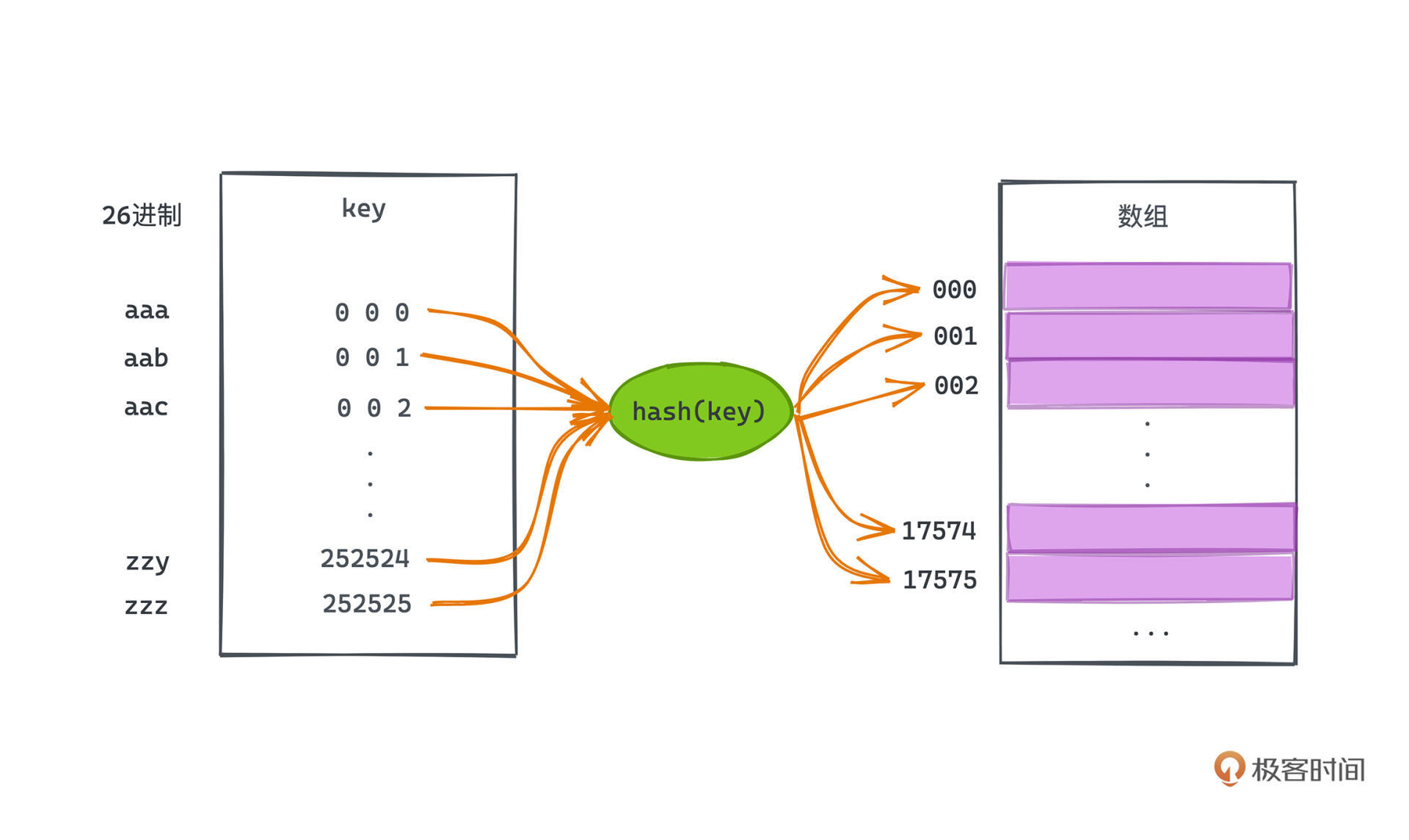
但设计一个合理的散列函数是一个非常有挑战的事情。比如,26进制的散列函数就有一个巨大的缺陷,就是它所需要的数组空间太大了,在刚刚的示例代码中,仅表示长度为3位的、只有a-z构成的字符串,就需要开一个接近20000(26^3)大小的计数数组。假设我们有一个单词是有10个字母,那所需要的26^10的计数数组,其下标甚至不能用一个长整型表示出来。
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
这种时候我们不得不做的事情可能是,对26进制的哈希值再进行一次对大质数取mod的运算,只有这样才能用比较有限的计数数组空间去表示整个哈希表。
|
|||
|
|
|
|||
|
|
然而,取了mod之后,我们很快就会发现,现在可能出现一种情况,把两个不同的单词用26进制表示并取模之后,得到的值很可能是一样的。这个问题被称之为**哈希碰撞**,当然也是一个需要处理的问题。
|
|||
|
|
|
|||
|
|
比如如果我们设置的数组大小只有16,那么AA和Q这两个字符串在26进制的哈希函数作用下就是,所对应的哈希表的数组下标就都是0。
|
|||
|
|
|
|||
|
|
好吧,计算机的世界问题总是这样接踵而至。就让我们来逐一解决吧。
|
|||
|
|
|
|||
|
|
## JDK的实现
|
|||
|
|
|
|||
|
|
现在,我们来好好考虑一下散列函数到底需要怎么设计。
|
|||
|
|
|
|||
|
|
* 整个散列表是建立在数组上的,显然首先要保证散列函数**输出的数值是一个非负整数**,因为这个整数将是散列表底层数组的下标。
|
|||
|
|
* 其次,底层数组的空间不可能是无限的。我们应该要让散列函数**在使用有限数组空间的前提下,导致的哈希冲突尽量少**。
|
|||
|
|
* 最后,我们当然也希望散列函数本身的**计算不过于复杂**。计算哈希虽然是一个常数的开销,但是反复执行一个复杂的散列函数显然也会拖慢整个程序。
|
|||
|
|
|
|||
|
|
带着这些思考,一起来看看JDK中对散列函数的选择吧。
|
|||
|
|
|
|||
|
|
在JDK(以JDK14为例)中Map的实现非常多,我们讲解的HashMap主要实现在 `java.util` 下的 `HashMap` 中,这是一个最简单的不考虑并发的、基于散列的Map实现。
|
|||
|
|
|
|||
|
|
找到用于计算哈希值的hash方法:
|
|||
|
|
|
|||
|
|
```java
|
|||
|
|
static final int hash(Object key) {
|
|||
|
|
int h;
|
|||
|
|
return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
|
|||
|
|
}
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
可以发现非常简短,就是对key.hashCode()进行了一次特别的位运算。你可能会对这里的,key.hashcode 和 h>>>16,有一些疑惑,我们来看一看。
|
|||
|
|
|
|||
|
|
### hashcode
|
|||
|
|
|
|||
|
|
而这里的hashCode,其实是Java一个非常不错的设计。在Java中每个对象生成时都会产生一个对应的hashcode。**当然数据类型不同,hashcode的计算方式是不一样的,但一定会保证的是两个一样的对象,对应的hashcode也是一样的**;
|
|||
|
|
|
|||
|
|
所以在比较两个对象是否相等时,我们可以先比较hashcode是否一致,如果不一致,就不需要继续调用equals,从统计意义上来说就大大降低了比较对象相等的代价。当然equals和hashcode的方法也是支持用户重写的。
|
|||
|
|
|
|||
|
|
既然今天要解决的问题是如何统计文本单词数量,我们就一起来看看JDK中对String类型的hashcode是怎么计算的吧,我们进入 `java.lang` 包查看String类型的实现:
|
|||
|
|
|
|||
|
|
```java
|
|||
|
|
public int hashCode() {
|
|||
|
|
// The hash or hashIsZero fields are subject to a benign data race,
|
|||
|
|
// making it crucial to ensure that any observable result of the
|
|||
|
|
// calculation in this method stays correct under any possible read of
|
|||
|
|
// these fields. Necessary restrictions to allow this to be correct
|
|||
|
|
// without explicit memory fences or similar concurrency primitives is
|
|||
|
|
// that we can ever only write to one of these two fields for a given
|
|||
|
|
// String instance, and that the computation is idempotent and derived
|
|||
|
|
// from immutable state
|
|||
|
|
int h = hash;
|
|||
|
|
if (h == 0 && !hashIsZero) {
|
|||
|
|
h = isLatin1() ? StringLatin1.hashCode(value)
|
|||
|
|
: StringUTF16.hashCode(value);
|
|||
|
|
if (h == 0) {
|
|||
|
|
hashIsZero = true;
|
|||
|
|
} else {
|
|||
|
|
hash = h;
|
|||
|
|
}
|
|||
|
|
}
|
|||
|
|
return h;
|
|||
|
|
}
|
|||
|
|
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
Latin和UTF16是两种字符串的编码格式,实现思路其实差不多,我们就来看`StringUTF16`中hashcode的实现:
|
|||
|
|
|
|||
|
|
```java
|
|||
|
|
public static int hashCode(byte[] value) {
|
|||
|
|
int h = 0;
|
|||
|
|
int length = value.length >> 1;
|
|||
|
|
for (int i = 0; i < length; i++) {
|
|||
|
|
h = 31 * h + getChar(value, i);
|
|||
|
|
}
|
|||
|
|
return h;
|
|||
|
|
}
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
啊哈!我们发现也没有多么高深嘛,就是对字符串逐位按照下面的方式进行计算,和展开成26进制的想法本质上是相似的。
|
|||
|
|
|
|||
|
|
```plain
|
|||
|
|
s[0]*31^(n-1) + s[1]*31^(n-2) + ... + s[n-1]
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
不过一个非常有趣的问题是为什么选择了31?
|
|||
|
|
|
|||
|
|
答案并不是那么直观。首先在各种哈希计算中,我们比较倾向使用奇素数进行乘法运算,而不是用偶数。因为用偶数,尤其是2的幂次,进行乘法,相当于直接对原来的数据进行移位运算;这样溢出的时候,部分位的信息就完全丢失了,可能增加哈希冲突的概率。
|
|||
|
|
|
|||
|
|
而为什么选择了31这个奇怪的数,这是因为计算机在进行移位运算要比普通乘法运算快得多,而31\*i可以直接转化为`(i << 5)- i` ,这是一个性能比较好的乘法计算方式,现代的编译器都可以推理并自动完成相关的优化。StackOverflow上有一个相关的[讨论](https://stackoverflow.com/a/299748)非常不错,也可以参考《effective Java》中的相关章节。
|
|||
|
|
|
|||
|
|
### h>>>16
|
|||
|
|
|
|||
|
|
好,我们现在来看 `^ h >>> 16` 又是一个什么样的作用呢?它的意思是就是将h右移16位并进行异或操作,不熟悉相关概念的同学可以参考[百度百科](https://baike.baidu.hk/item/%E7%A7%BB%E4%BD%8D%E9%81%8B%E7%AE%97%E7%AC%A6/5622348)。为什么要这么做呢?
|
|||
|
|
|
|||
|
|
哦,这里要先跟你解释一下,刚刚那个hash值计算出来这么大,怎么把它连续地映射到一个小一点的连续数组空间呢?想必你已经猜到了,就是前面说的取模,我们需要将hash值对数组的大小进行一次取模。
|
|||
|
|
|
|||
|
|
那数组大小是多少呢?在 HashMap 中,用于存储所有的{Key,Value}对的真实数组 table ,有一个初始化的容量,但随着插入的元素越来越多,数组的resize机制会被触发,而扩容时,容量永远是2的幂次,这也是为了保证取模运算的高效。马上讲具体实现的时候会展开讲解。
|
|||
|
|
|
|||
|
|
总而言之,我们需要对2的幂次大小的数组进行一次取模计算。但前面也说了**对二的幂次取模相当于直接截取数字比较低的若干位,这在数组元素较少的时候,相当于只使用了数字比较低位的信息**,而放弃了高位的信息,可能会增加冲突的概率。
|
|||
|
|
|
|||
|
|
所以,JDK的代码引入了`^ h >>> 16` 这样的位运算,其实就是把高16位的信息叠加到了低16位,这样我们在取模的时候就可以用到高位的信息了。
|
|||
|
|
|
|||
|
|
当然,无论我们选择多优秀的hash函数,只要是把一个更大的空间映射到一个更小的连续数组空间上,那哈希冲突一定是无可避免的。那如何处理冲突呢?
|
|||
|
|
|
|||
|
|
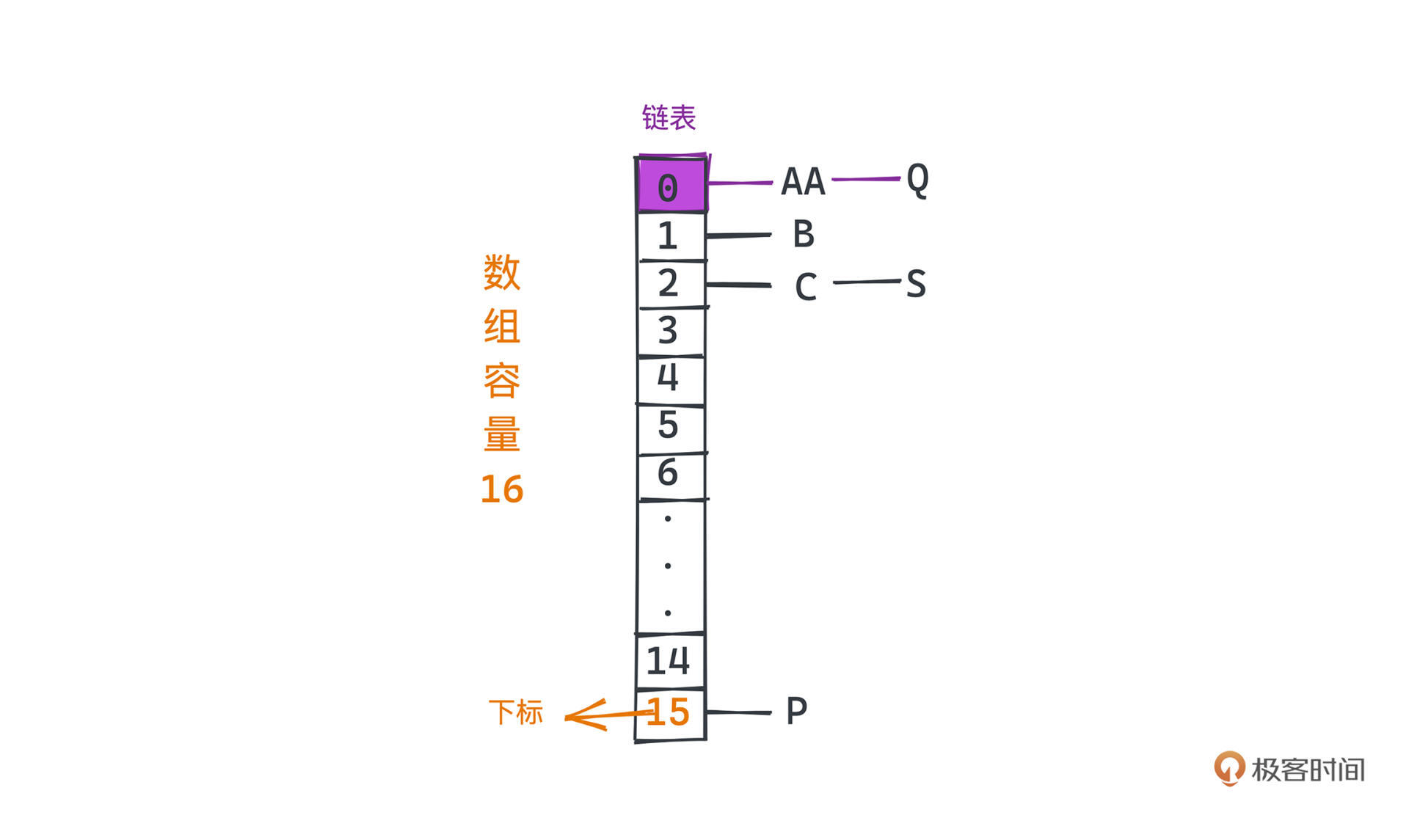
JDK中采用的是开链法。
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
哈希表内置数组中的每个槽位,存储的是一个链表,链表节点的值存放的就是需要存储的键值对。如果碰到哈希冲突,也就是两个不同的key映射到了数组中的同一个槽位,我们就将该元素直接放到槽位对应链表的尾部。
|
|||
|
|
|
|||
|
|
### JDK代码实现
|
|||
|
|
|
|||
|
|
现在,在JDK中具体实现的代码就很好理解啦,table 就是经过散列之后映射到的内部连续数组:
|
|||
|
|
|
|||
|
|
```java
|
|||
|
|
transient Node<K,V>[] table;
|
|||
|
|
final V putVal(int hash, K key, V value, boolean onlyIfAbsent,
|
|||
|
|
boolean evict) {
|
|||
|
|
Node<K,V>[] tab; Node<K,V> p; int n, i;
|
|||
|
|
//在tab尚未初始化、或者对应槽位链表未初始化时,进行相应的初始化操作
|
|||
|
|
if ((tab = table) == null || (n = tab.length) == 0)
|
|||
|
|
n = (tab = resize()).length;
|
|||
|
|
if ((p = tab[i = (n - 1) & hash]) == null)
|
|||
|
|
tab[i] = newNode(hash, key, value, null);
|
|||
|
|
else {
|
|||
|
|
Node<K,V> e; K k;
|
|||
|
|
// 查找 key 对应的节点
|
|||
|
|
if (p.hash == hash &&
|
|||
|
|
((k = p.key) == key || (key != null && key.equals(k))))
|
|||
|
|
e = p;
|
|||
|
|
else if (p instanceof TreeNode)
|
|||
|
|
e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value);
|
|||
|
|
else {
|
|||
|
|
// 遍历所有节点 依次查找
|
|||
|
|
for (int binCount = 0; ; ++binCount) {
|
|||
|
|
if ((e = p.next) == null) {
|
|||
|
|
p.next = newNode(hash, key, value, null);
|
|||
|
|
if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st
|
|||
|
|
treeifyBin(tab, hash);
|
|||
|
|
break;
|
|||
|
|
}
|
|||
|
|
if (e.hash == hash &&
|
|||
|
|
((k = e.key) == key || (key != null && key.equals(k))))
|
|||
|
|
break;
|
|||
|
|
p = e;
|
|||
|
|
}
|
|||
|
|
}
|
|||
|
|
if (e != null) { // existing mapping for key
|
|||
|
|
V oldValue = e.value;
|
|||
|
|
if (!onlyIfAbsent || oldValue == null)
|
|||
|
|
e.value = value;
|
|||
|
|
afterNodeAccess(e);
|
|||
|
|
return oldValue;
|
|||
|
|
}
|
|||
|
|
}
|
|||
|
|
++modCount;
|
|||
|
|
if (++size > threshold)
|
|||
|
|
resize();
|
|||
|
|
afterNodeInsertion(evict);
|
|||
|
|
return null;
|
|||
|
|
}
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
通过hash函数的计算,我们可以基于这个数组的下标快速访问到key对应的元素,元素存储的是Node类型。
|
|||
|
|
|
|||
|
|
估计你会注意到第21行进行了一个treeifyBin的操作,就是说当哈希冲突产生的链表足够长时,我们就会把它转化成有序的红黑树,以提高对同样hash值的不同key的查找速度。
|
|||
|
|
|
|||
|
|
这是因为在HashMap中Node具体的实现可以是链表或者红黑树。用红黑树的整体思想和开链是一样的,这只是在冲突比较多、链表比较长的情况下的一个优化,具体结构和JDK中另一种典型的Map实现TreeMap一致,我们会在下一讲详细介绍。
|
|||
|
|
|
|||
|
|
好,我们回头看整体的逻辑。
|
|||
|
|
|
|||
|
|
开始的5-8行主要是为了在tab尚未初始化、或者对应槽位链表未初始化时进行相应的初始化操作。**从16行开始,就进入了和待插入key的hash值所对应的链表逐一对比的阶段**,目标是找到一个合适的槽位,找到当前链表中的key和待插入的key相同的节点,或者直到遍历到链表的尾部;而如果节点类型是红黑树的话,底层就直接调用了红黑树的查找方法。
|
|||
|
|
|
|||
|
|
这里还有一个比较重要的操作就是第40行的resize函数,帮助动态调整数组所占用的空间,也就是底层的连续数组table的大小。
|
|||
|
|
|
|||
|
|
```java
|
|||
|
|
if (++size > threshold)
|
|||
|
|
resize();
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
随着插入的数据越来越多,如果保持table大小不变,一定会遇到更多的哈希冲突,这会让哈希表性能大大下降。所以我们有必要在插入数据越来越多的时候进行哈希表的扩容,也就是resize操作。
|
|||
|
|
|
|||
|
|
这里的threshold就是我们触发扩容机制的阈值,每次插入数据时,如果发现表内的元素多于threshold之后,就会进行resize操作:
|
|||
|
|
|
|||
|
|
```java
|
|||
|
|
final Node<K,V>[] resize() {
|
|||
|
|
Node<K,V>[] oldTab = table;
|
|||
|
|
int oldCap = (oldTab == null) ? 0 : oldTab.length;
|
|||
|
|
int oldThr = threshold;
|
|||
|
|
int newCap, newThr = 0;
|
|||
|
|
if (oldCap > 0) {
|
|||
|
|
if (oldCap >= MAXIMUM_CAPACITY) {
|
|||
|
|
threshold = Integer.MAX_VALUE;
|
|||
|
|
return oldTab;
|
|||
|
|
}
|
|||
|
|
else if ((newCap = oldCap << 1) < MAXIMUM_CAPACITY &&
|
|||
|
|
oldCap >= DEFAULT_INITIAL_CAPACITY)
|
|||
|
|
newThr = oldThr << 1; // 翻倍扩容
|
|||
|
|
}
|
|||
|
|
else if (oldThr > 0) // 初始化的时候 capacity 设置为初始化阈值
|
|||
|
|
newCap = oldThr;
|
|||
|
|
else { // 没有初始化 采用默认值
|
|||
|
|
newCap = DEFAULT_INITIAL_CAPACITY;
|
|||
|
|
newThr = (int)(DEFAULT_LOAD_FACTOR * DEFAULT_INITIAL_CAPACITY);
|
|||
|
|
}
|
|||
|
|
if (newThr == 0) {
|
|||
|
|
float ft = (float)newCap * loadFactor; // 用容量乘负载因子表示扩容阈值
|
|||
|
|
newThr = (newCap < MAXIMUM_CAPACITY && ft < (float)MAXIMUM_CAPACITY ?
|
|||
|
|
(int)ft : Integer.MAX_VALUE);
|
|||
|
|
}
|
|||
|
|
threshold = newThr;
|
|||
|
|
@SuppressWarnings({"rawtypes","unchecked"})
|
|||
|
|
Node<K,V>[] newTab = (Node<K,V>[])new Node[newCap];
|
|||
|
|
table = newTab;
|
|||
|
|
if (oldTab != null) {
|
|||
|
|
for (int j = 0; j < oldCap; ++j) {
|
|||
|
|
Node<K,V> e;
|
|||
|
|
if ((e = oldTab[j]) != null) {
|
|||
|
|
oldTab[j] = null;
|
|||
|
|
if (e.next == null)
|
|||
|
|
newTab[e.hash & (newCap - 1)] = e;
|
|||
|
|
else if (e instanceof TreeNode)
|
|||
|
|
((TreeNode<K,V>)e).split(this, newTab, j, oldCap);
|
|||
|
|
else {
|
|||
|
|
// 新扩容部分,标识为hi,原来的部分标识为lo
|
|||
|
|
// JDK 1.8 之后引入用于解决多线程死循环问题 可参考:https://stackoverflow.com/questions/35534906/java-hashmap-getobject-infinite-loop
|
|||
|
|
Node<K,V> loHead = null, loTail = null;
|
|||
|
|
Node<K,V> hiHead = null, hiTail = null;
|
|||
|
|
Node<K,V> next;
|
|||
|
|
// 整体操作就是将j所对应的链表拆成两个部分
|
|||
|
|
// 分别放到 j 和 j + oldCap 的槽位
|
|||
|
|
do {
|
|||
|
|
next = e.next;
|
|||
|
|
if ((e.hash & oldCap) == 0) {
|
|||
|
|
if (loTail == null)
|
|||
|
|
loHead = e;
|
|||
|
|
else
|
|||
|
|
loTail.next = e;
|
|||
|
|
loTail = e;
|
|||
|
|
}
|
|||
|
|
else {
|
|||
|
|
if (hiTail == null)
|
|||
|
|
hiHead = e;
|
|||
|
|
else
|
|||
|
|
hiTail.next = e;
|
|||
|
|
hiTail = e;
|
|||
|
|
}
|
|||
|
|
} while ((e = next) != null);
|
|||
|
|
if (loTail != null) {
|
|||
|
|
loTail.next = null;
|
|||
|
|
newTab[j] = loHead;
|
|||
|
|
}
|
|||
|
|
if (hiTail != null) {
|
|||
|
|
hiTail.next = null;
|
|||
|
|
newTab[j + oldCap] = hiHead;
|
|||
|
|
}
|
|||
|
|
}
|
|||
|
|
}
|
|||
|
|
}
|
|||
|
|
}
|
|||
|
|
return newTab;
|
|||
|
|
}
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
看起来 resize 的代码比较复杂,但核心在做的事情很简单,就是要将哈希桶也就是内置的table数组,搬到一个更大的数组中去。主要有两块逻辑我们需要关注一下。
|
|||
|
|
|
|||
|
|
第一部分在第6-26行,主要的工作就是计算当前扩容的数组大小和触发下一次扩容的阈值threshold。
|
|||
|
|
|
|||
|
|
可以看到命中扩容条件的分支都会进入13行的逻辑,也就是每次扩容我们都会扩容一倍的容量。这和c++中STL动态数组的扩容逻辑是相似的,都是为了平衡扩容带来的时间复杂度和占用空间大小的权衡;当然这也是因为我们仍然需要保持数组大小为2的幂次,以提高取模运算的速度。其他行主要是为了处理一些默认参数和初始化的逻辑。
|
|||
|
|
|
|||
|
|
在第22行中,我们还会看到一个很重要的变量loadfactor,也就是负载因子。这是创建HashMap时的一个可选参数,用来帮助我们计算下一次触发扩容的阈值。假设 length 是table的长度,threshold = length \* Load factor。在内置数组大小一定的时候,负载因子越高,触发resize的阈值也就越高;
|
|||
|
|
|
|||
|
|
负载因子默认值0.75,是基于经验对空间和时间效率的平衡,如果没有特殊的需求可以不用修改。loadfactor越高,随着插入的元素越来越多,可能导致冲突的概率也会变高;当然也会让我们有机会使用更小的内存,避免更多次的扩容操作。
|
|||
|
|
|
|||
|
|
## 总结
|
|||
|
|
|
|||
|
|
好,今天关于HashMap源码的分析就到这里啦。红黑树的部分我们下一节讲解TreeMap的时候再好好讨论,到时候你就会知道红黑树和链表之间的性能差距,也能体会到构造可快速访问键值对集合的另一种思路。
|
|||
|
|
|
|||
|
|

|
|||
|
|
|
|||
|
|
现在,如果不借助系统自带的HashMap,相信你应该也可以手写数据结构统计单词的数量了吧?正确的思路就是,根据全文长度大概预估一下会有多少个单词,开一个数倍于它的数组,再设计一个合理的hash函数,把每个单词映射到数组的某个下标,用这个数组计数统计就好啦。
|
|||
|
|
|
|||
|
|
当然在实际工程中,我们不会为每个场景都单独写一个这样的散列表实现,也不用自己去处理复杂的扩容场景。JDK的HashMap或者STL的unordered\_map都是非常优秀的散列表实现,你可以好好学习一下相关源码。当然,你也可能会注意到我们在代码中没有任何处理并发的逻辑,这当然导致了线程不安全,在需要保证线程安全的场合可以用ConcurrentHashMap替换。
|
|||
|
|
|
|||
|
|
## 课后作业
|
|||
|
|
|
|||
|
|
前面我们有提到loadfactor,建议不要修改,那你知道什么时候需要修改吗?欢迎你在评论区和我一起讨论。
|
|||
|
|
|
|||
|
|
### 拓展资料
|
|||
|
|
|
|||
|
|
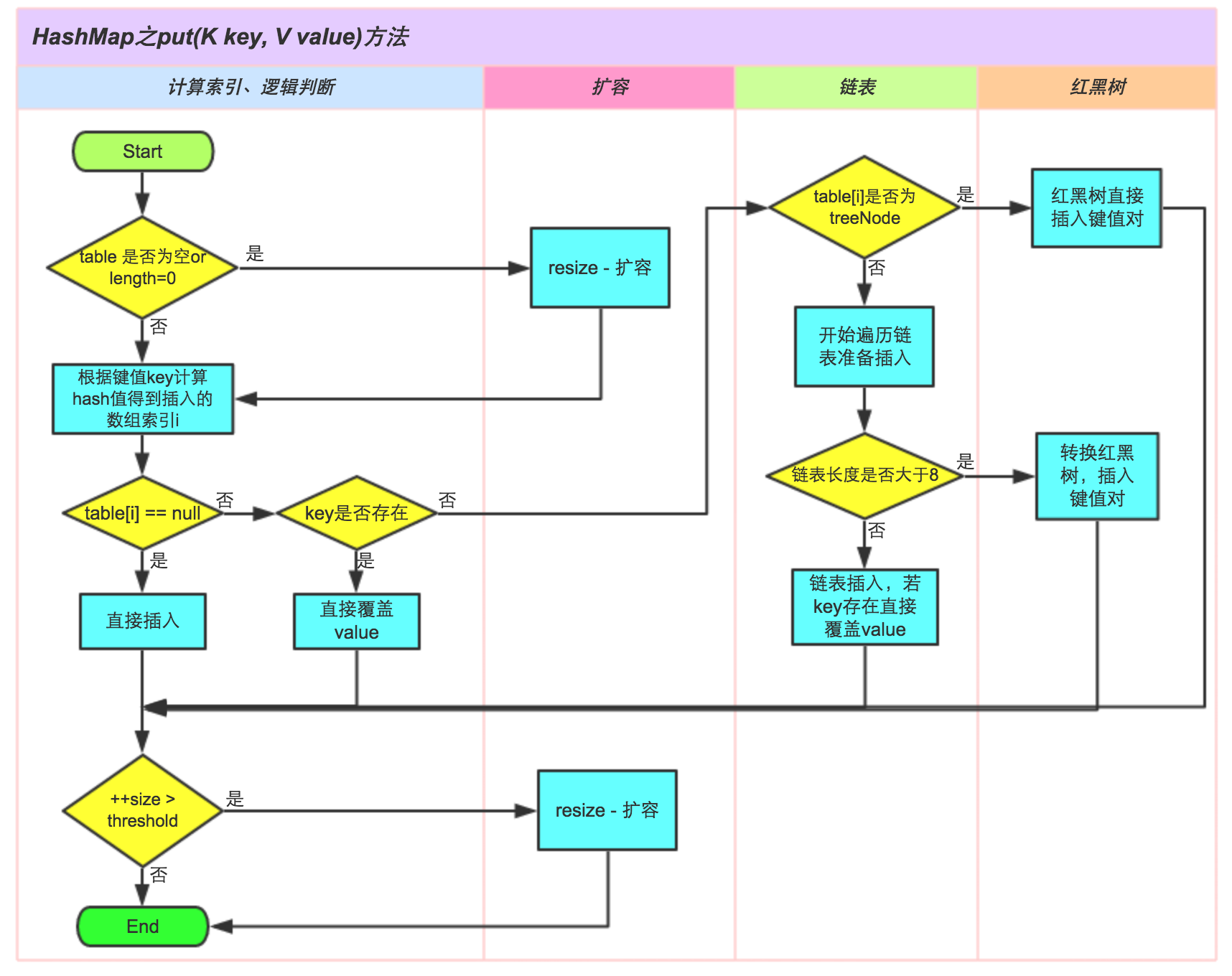
关于HashMap的put操作,美团总结了一个非常不错的[流程图](https://tech.meituan.com/2016/06/24/java-hashmap.html),可以参考。
|
|||
|
|
|
|||
|
|
|