304 lines
22 KiB
Markdown
304 lines
22 KiB
Markdown
|
|
# 11|忘记加“盐”:加密结果强度不够吗?
|
|||
|
|
|
|||
|
|
你好,我是王昊天。今天我来和你一起来聊聊“盐”。
|
|||
|
|
|
|||
|
|
什么是盐?
|
|||
|
|
|
|||
|
|
食盐是一种调味品,可以在烹饪食物时添加到菜肴中,给寡淡的食材增添风味。恰好我对烹饪也有一点研究,所以对食盐的作用也稍有理解。食盐是菜品中咸味的主要来源,在烹饪中加入适量的食盐,一方面可以提鲜,另一方面也可以去除掉原料的一些异味。
|
|||
|
|
|
|||
|
|
那么盐和安全有什么关系呢?
|
|||
|
|
|
|||
|
|
盐又称为Salt,在密码学中我们常常会用到散列算法对字符串进行处理,散列算法可以为数据创建相对精简的数据指纹,具体我们会在后面详细介绍。为了提高安全性,**在进行散列操作之前会对字符串进行一些拼接、混淆操作,这个过程我们就称为“加盐”**。虽然不知道“加盐”的本意是否如此,但加盐处理字符串的过程与使用盐处理食物的过程非常相似,**一方面去除了字符串本身的特征,另一方面增强了字符串的复杂度。**
|
|||
|
|
|
|||
|
|
经过加盐处理的散列结果与未加盐处理的散列结果,极大概率是不相同的,这一过程大大提高了散列算法的安全性。
|
|||
|
|
|
|||
|
|
## HASH
|
|||
|
|
|
|||
|
|
在了解调味品该如何使用之前,我们要先了解原材料是什么。因此,在了解如何用盐之前,我们先来了解HASH函数是什么。
|
|||
|
|
|
|||
|
|
**HASH函数,又称散列函数,是为一段数据创建数字指纹的方法,创建生成的数字指纹叫散列值。**由于经过了压缩,它的长度较原始输入短了很多,因此我们也称之为摘要。
|
|||
|
|
|
|||
|
|
由HASH函数计算出来的散列值**具有不可逆的特性**,这里说的不可逆,是指攻击者无法从散列值进行逆向推导,进而获得原始输入。得益于不可逆特性,在Web业务系统开发过程中,我们通常使用散列值作为用户密码存储进数据库。在这种情况下,Web业务系统既可以校验用户密码的正确性,又无法真正得知用户密码明文。
|
|||
|
|
|
|||
|
|
**HASH的应用**
|
|||
|
|
|
|||
|
|
HASH函数具备很多优秀的特性,比如计算不可逆、难以伪造、数据压缩等,因此它具备很多应用场景。
|
|||
|
|
|
|||
|
|
**基于计算不可逆和难以伪造这两个优秀的安全特性,HASH函数的一个主要应用场景,就是校验数据传递的完整性。**将要传递的数据作为HASH函数的输入,生成散列值A;再在接收端将A作为HASH函数的输入,生成散列值B。通过对比A和B,就可以快速判断出数据传输的完整性和数据的真实性。
|
|||
|
|
|
|||
|
|
许多官方发布的应用、开发组件和二进制可执行程序,都会在下载链接旁边附上对应的散列值,方便终端用户在下载完成之后进行对比。这种方式可以保证终端用户,即使遭遇了DNS污染,中间人攻击,或者官方遭遇入侵导致安装包被替换的情况,也可以清晰地判断出恶意应用。
|
|||
|
|
|
|||
|
|
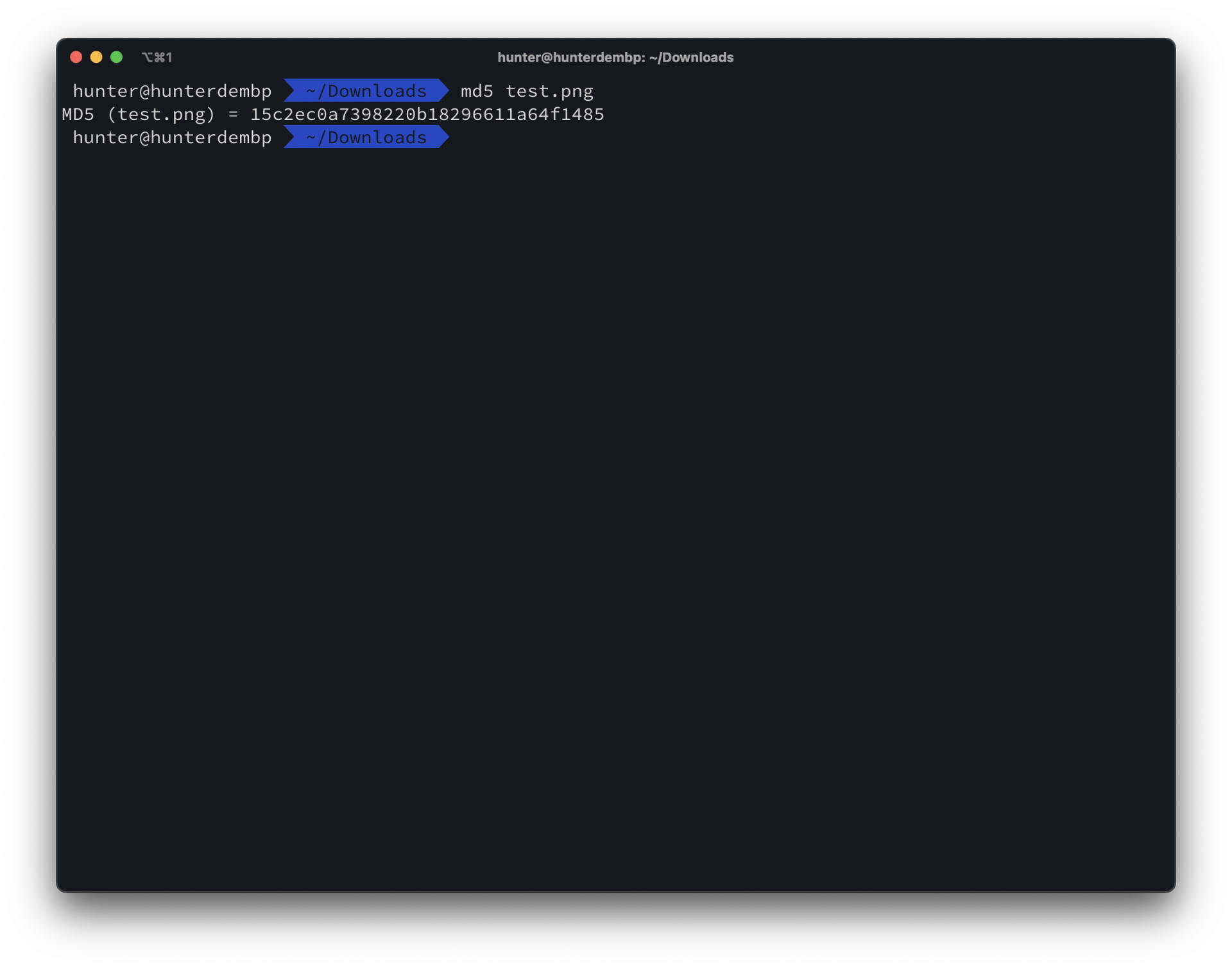
这是一个我经常玩的游戏(没有收广告费),在官网下载链接页面可以看到提供的MD5散列值:
|
|||
|
|
|
|||
|
|

|
|||
|
|
|
|||
|
|
下载之后要如何操作呢?其实是非常简单的,以Mac OS为例,在Terminal里已经集成了md5命令,我们可以通过md5命令快速计算出一个文件的md5散列值,将其与官网展示的散列值进行对比即可:
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
**基于数据压缩特性,则会有散列表和错误校正等应用场景。**
|
|||
|
|
|
|||
|
|
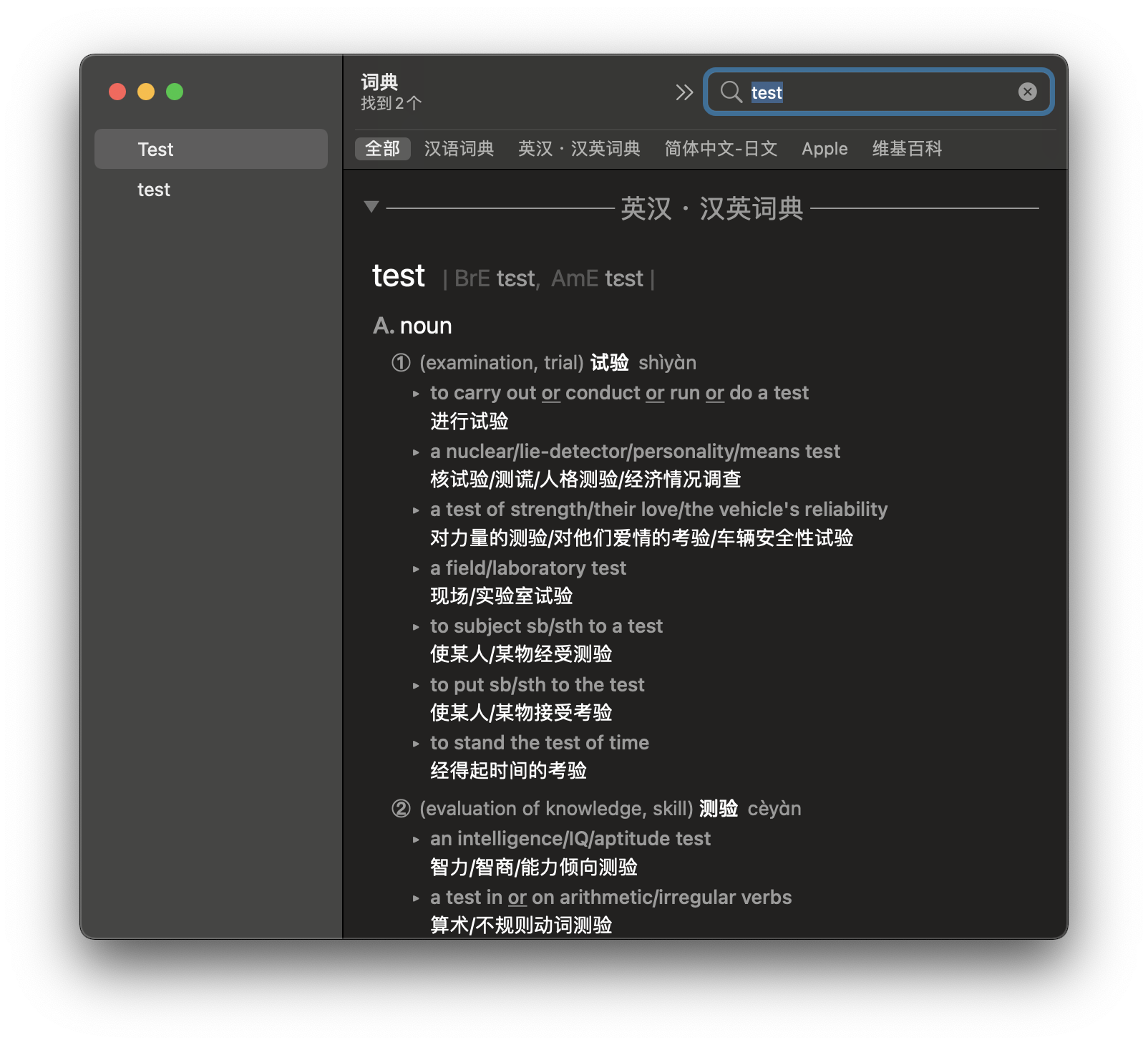
散列表是一种开发中常用的技术手段,它通常被用来根据关键字快速查找数据记录。比较形象的例子是字典,它的关键词是英文单词,而完整的记录则包含了单词的拼写、音标、解释以及例句,这个场景可以理解为一种,从完整的数据记录到单词的映射关系。
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
错误校正,是开发中常用的另一种技术手段,在数据传输、存储的过程中经常会用到。在数据传输、存储的过程中,由于信号的干扰、物理介质的不稳定性等原因,经常会出现数据错误的情况。这时,我们可以通过计算散列值的方法来判断数据完整性,这种方案就称为**冗余校验**。更进一步,我们甚至可以通过定义不同的HASH函数,使得冗余校验具备纠错能力。
|
|||
|
|
|
|||
|
|
## 盐
|
|||
|
|
|
|||
|
|
用户账户认证过程,通常涉及到密码的存储,**这就是盐的主要应用场景之一**。
|
|||
|
|
|
|||
|
|
我们都知道,密码的存储通常是放在数据库中,关于密码的存储形态有很多种,通常可选的方案包括明文、散列值等。
|
|||
|
|
|
|||
|
|
如果采用明文存储的方案,一旦发生了入侵事件,或者系统存在漏洞使得数据库外泄,就会导致大规模的用户账户外泄,这种安全事件是灾难性的。所以目前大部分系统采取的方案都是存储散列值,在这种情况下,即使是系统也无法得知用户的密码是什么。
|
|||
|
|
|
|||
|
|
通常在采用存储散列值的情况下,系统会通过比较散列值来认证用户。系统通过用户输入获得密码后,会让密码经过HASH函数处理产生一个散列值,并将该散列值与存储在数据库中的散列值进行对比,如果相同则表示认证成功。
|
|||
|
|
|
|||
|
|
我们可以设想一下,在这种方案下,即使黑客通过漏洞成功获得了数据库内的全部数据,他获得的,也仅仅是密码经过HASH函数运算得出的散列值,而这个散列值并不能够帮助他登录系统。
|
|||
|
|
|
|||
|
|
## 暴力破解和字典攻击
|
|||
|
|
|
|||
|
|
为了达到登录的目的,黑客必须找到一段数据,这段数据的HASH运算结果需要与黑客获得的散列值一致。**此时黑客可选的方案是暴力破解、字典攻击和彩虹表攻击。**
|
|||
|
|
|
|||
|
|
这三种攻击方式执行的难度由简单到困难,效果也是从差到好。暴力破解和字典攻击的实施过程都非常简单,**基本思路都是通过遍历用户密码所有取值来直接找到答案,区别是暴力破解采用遍历的方式是实时计算,而字典攻击会根据预先计算好的结果直接查找。**虽然这两种方案执行上非常简单,但实际操作效果却并不理想,主要原因是用户密码的取值空间过于庞大。
|
|||
|
|
|
|||
|
|
这里我们通过简单的计算,来对取值空间有一个更加直观的认识。一般用户密码的单字符可选范围是26个小写字母、26个大写字母、10个数字以及少数特殊字符,我们假设用户密码是8位(要知道8位密码并不算强度很高的设置),那么经过计算,密码合计取值范围就是72万亿。
|
|||
|
|
|
|||
|
|
```plain
|
|||
|
|
单字符取值范围 ≈ 26 + 26 + 10 + 10 = 72
|
|||
|
|
8个字符的密码取值空间 = 72 ^ 8 = 722204136308736 ≈ 72万亿
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
按照每秒能够计算100万个密码的散列值来计算,需要大约8358天,相当于22.9年才能完成密码空间的遍历,很显然这种攻击是无法真正实施的,**因此暴力破解攻击无效**。
|
|||
|
|
|
|||
|
|
```plain
|
|||
|
|
722204136308736 / (1000000 * 3600 * 24) ≈ 8358
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
按照每个8位密码占据8个字节的存储空间来计算,72万亿的密码空间大约会占据5254TB的存储空间,很显然这种攻击也是无法真正实施的,**因此字典攻击也是无效的**。
|
|||
|
|
|
|||
|
|
```plain
|
|||
|
|
722204136308736 * 8.0 / (1024 * 1024 * 1024 * 1024) ≈ 5254
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
综合上面的分析,我们可以发现,暴力破解没有空间占用但时间消耗过大,而字典攻击几乎没有时间占用但空间消耗过大。因此,为了有效地对散列值进行攻击,我们需要一种更可行的方案。在这种方案里,我们能够接受多一些的解密时间,但希望它不要占用过大的空间。目前,这种平衡了时间和空间的攻击方案就是**彩虹表攻击**。
|
|||
|
|
|
|||
|
|
## 彩虹表攻击
|
|||
|
|
|
|||
|
|
### HASH链
|
|||
|
|
|
|||
|
|
以字典攻击为基础,通过算法设计来实现时间换取空间的效果,就是彩虹表攻击的原理。
|
|||
|
|
|
|||
|
|
彩虹表攻击中所涉及的算法就是**预计算的HASH链**。
|
|||
|
|
|
|||
|
|
为了实现预计算的HASH链,我们需要一个新型函数的辅助,一般会称之为归约函数或者约简函数。但是千万不要为这个名字感到困惑,它其实并没有真实地表达什么含义,你可以简单地理解为一个新函数R。**R函数与HASH函数执行相反的运算流程**,比如,HASH函数将原始输入映射到HASH散列值,而R函数则是将HASH散列值映射回原始输入,并且R函数的映射关系是可以任意指定的。
|
|||
|
|
|
|||
|
|
接下来我来带你实际构建一个HASH链,在这个过程中,你将对稍显复杂的彩虹表攻击有更直观的理解。
|
|||
|
|
|
|||
|
|
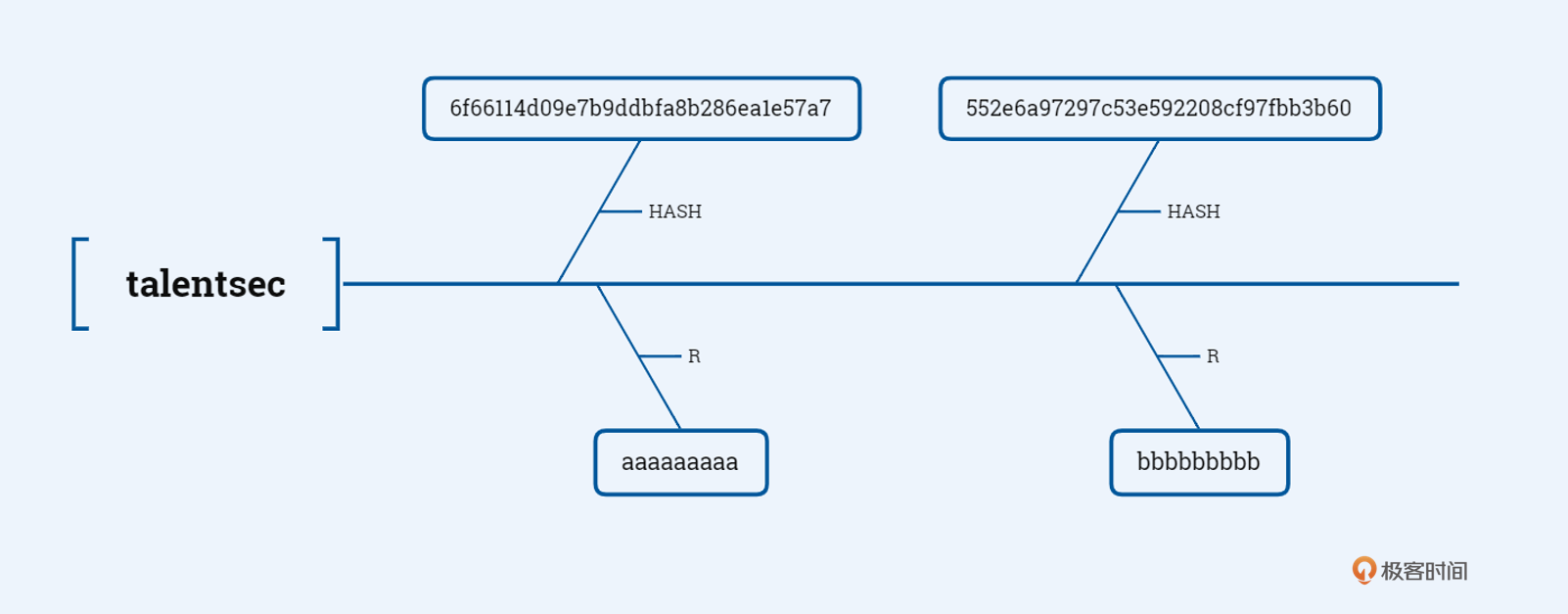
以MD5散列为例,首先我们随机选择一段明文`talentsec`并对其取md5散列,获得结果`6f66114d09e7b9ddbfa8b286ea1e57a7`,接下来我们按照自己的喜好定义一个R函数,并且使用R函数对散列值`6f66114d09e7b9ddbfa8b286ea1e57a7`进行运算,获得结果`aaaaaaaaa`。继续重复上述过程,即不断使用HASH函数和R函数进行计算,产生的如下链条就是HASH链:
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
通过随机选择多段明文重复执行这个过程,会产生多个HASH链,这些HASH链我们称为预计算的HASH链集。需要注意的是,存储的过程中我们只需要保存HASH链的头和尾,对于上述示例HASH链,我们只进行了2轮计算,所以其存储形态应该是`(talentsec,bbbbbbbbb)`。
|
|||
|
|
|
|||
|
|
那么我们要如何使用预计算的HASH链来进行攻击呢?
|
|||
|
|
|
|||
|
|
作为攻击者,我们需要破解一个HASH散列值。通过对该散列值进行多轮次的R函数、HASH函数计算,我们可以取得多个原始输入,如果原始输入与HASH链的头或者尾产生碰撞,HASH散列值的破解结果则很有可能存在于该链条中。
|
|||
|
|
|
|||
|
|
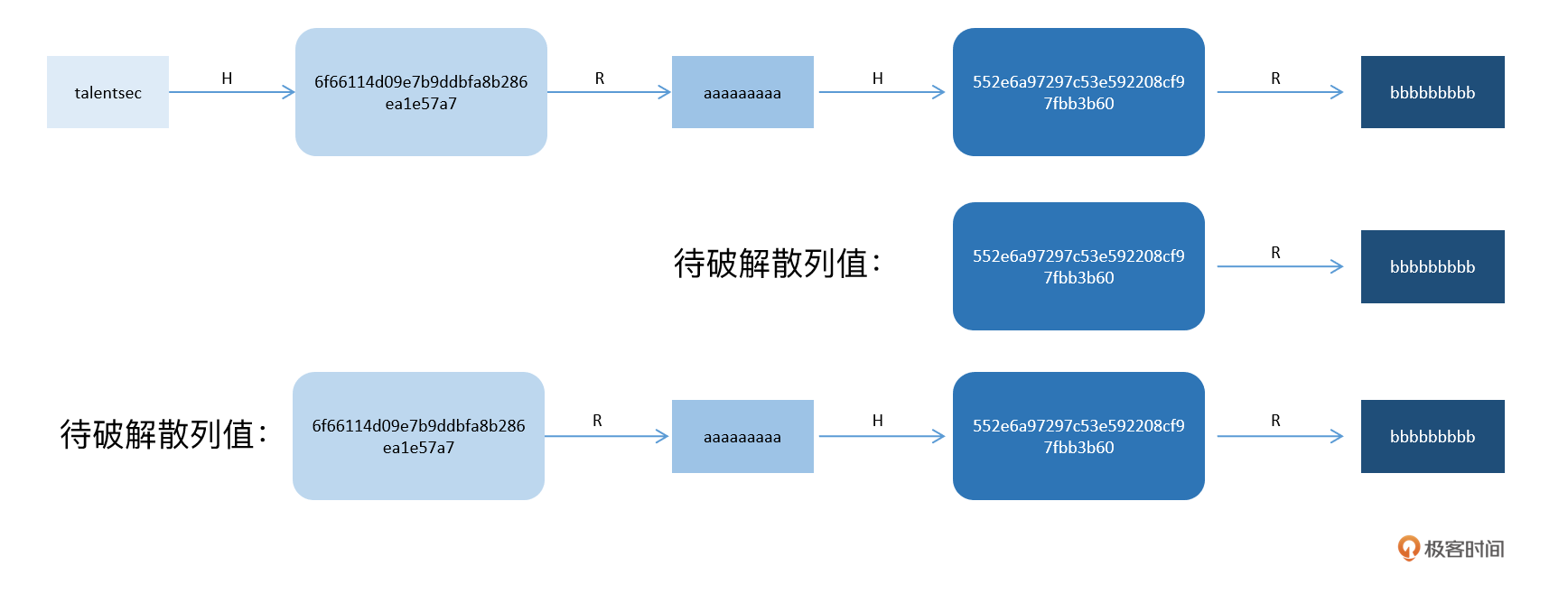
这里我们通过2个场景示例来直接感受一下,对于上述场景,如果我们希望破解的散列值是`552e6a97297c53e592208cf97fbb3b6`,通过1次R函数可以获得原始输入`bbbbbbbbb`,成功匹配到HASH链`(talentsec,bbbbbbbbb)`,通过从头执行HASH链的计算过程,可以得出破解结果是`aaaaaaaaa`;同样是上述场景,如果我们希望破解的散列值是`6f66114d09e7b9ddbfa8b286ea1e57a7`,通过R函数-HASH函数-R函数计算可以获得原始输入`bbbbbbbbb`,依然成功匹配到HASH链`(talentsec,bbbbbbbbb)`,通过从头执行HASH链的计算过程,可以得出破解结果是`talentsec`。
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
值得一提的是,破解中需要的运算轮次,一般与HASH链的计算轮次相同,如果达到了计算轮次却并未找到匹配的HASH链,则直接返回破解失败。
|
|||
|
|
|
|||
|
|
关于预计算HASH链的理想性能表现,我们可以通过简单的计算来分析。依然是8位密码的情况,假设我们定义了一个R函数,让每条HASH链能够执行1亿次计算,那么完成HASH链集的存储只需要大约220MB的空间。
|
|||
|
|
|
|||
|
|
```plain
|
|||
|
|
722204136308736 / 50000000 ≈ 14444082 条HASH链
|
|||
|
|
722204136308736 * 16 / (50000000 * 1024 * 1024) ≈ 220 MB
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
依然按照每秒100万次的速度来计算,单一HASH散列值从生成一条新的HASH链到完成匹配的时间预计不超过2分钟。
|
|||
|
|
|
|||
|
|
```plain
|
|||
|
|
100000000 / (1000000 * 60) ≈ 1.67 mins
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
### 彩虹表
|
|||
|
|
|
|||
|
|
那么,预计算的HASH链集就是彩虹表吗?其实并非如此。
|
|||
|
|
|
|||
|
|
预计算的HASH链集仍然存在着一些不足,主要是在性能表现方面。我们刚刚计算的攻击时间都是在理想情况下推演出来的,但是未经优秀设计就生成的预计算HASH链集,实际上并不能达到这个性能水平,因此才会出现彩虹表。**我们可以将彩虹表理解为是一种经过精密设计的预计算HASH链集,在攻击时能发挥出理想的性能表现。**
|
|||
|
|
|
|||
|
|
那么预计算HASH链集需要优化的核心点是哪里呢?接下来我们就一起来分析一下。
|
|||
|
|
|
|||
|
|
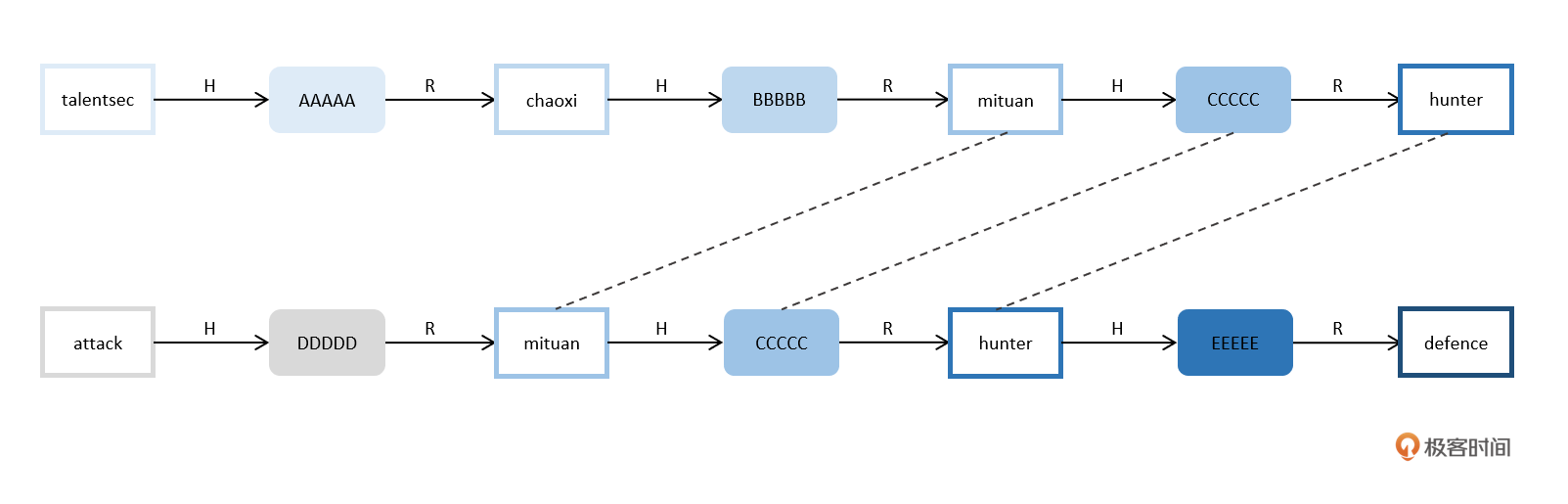
通过前面我们所讨论的攻击过程,不难判断,**预计算的HASH链集包含多条HASH链**,这一点我们从它的名字也不难看出,而每条HASH链能够覆盖的攻击范围,与它执行的计算次数呈现线性相关。最理想的情况当然是,每条HASH链所覆盖的攻击范围彼此互斥,这样在n条链的情况下,覆盖的攻击范围就是`n x 单链计算次数/2`。但现实往往没有这么理想,R函数的选择与设计可能会导致碰撞情况的发生:
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
通过上述示例可以发现,存在设计缺陷的R函数会导致大量碰撞的发生,而一旦中间某节点发生碰撞,就会导致后续节点全部碰撞,这样会大大缩小预计算HASH链集能够覆盖的攻击范围。又因为预计算HASH链只保存收尾节点,因此想要发现两条链的高度相似性是非常难的。
|
|||
|
|
|
|||
|
|
**彩虹表的出现正是为了解决R函数引起的链碰撞问题。**
|
|||
|
|
|
|||
|
|
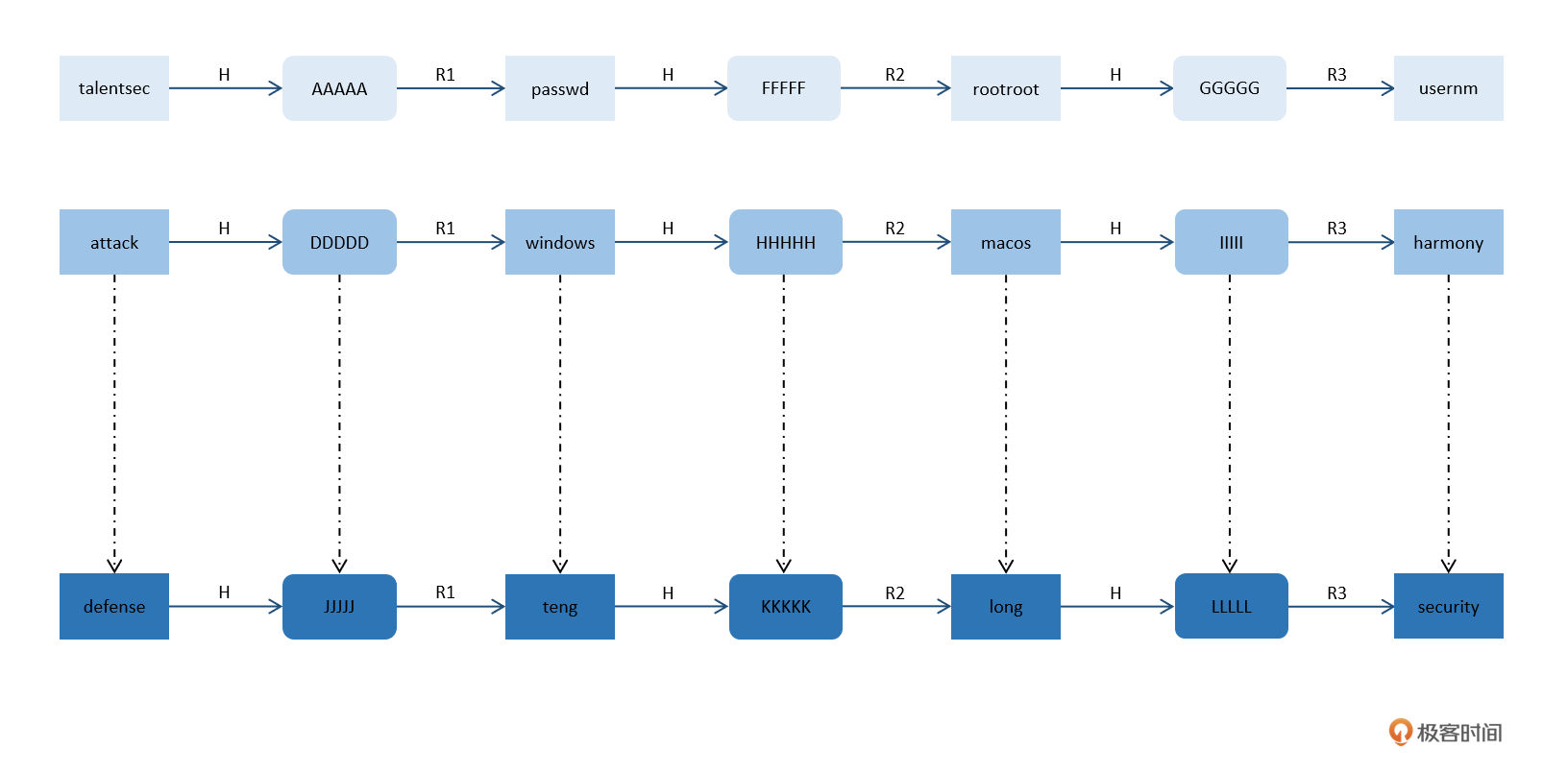
彩虹表的设计理念是,在生成预计算的HASH链时采用多种R函数,也就是在每个轮次的计算中分别使用R1、R2、R3函数等,大致含义如下:
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
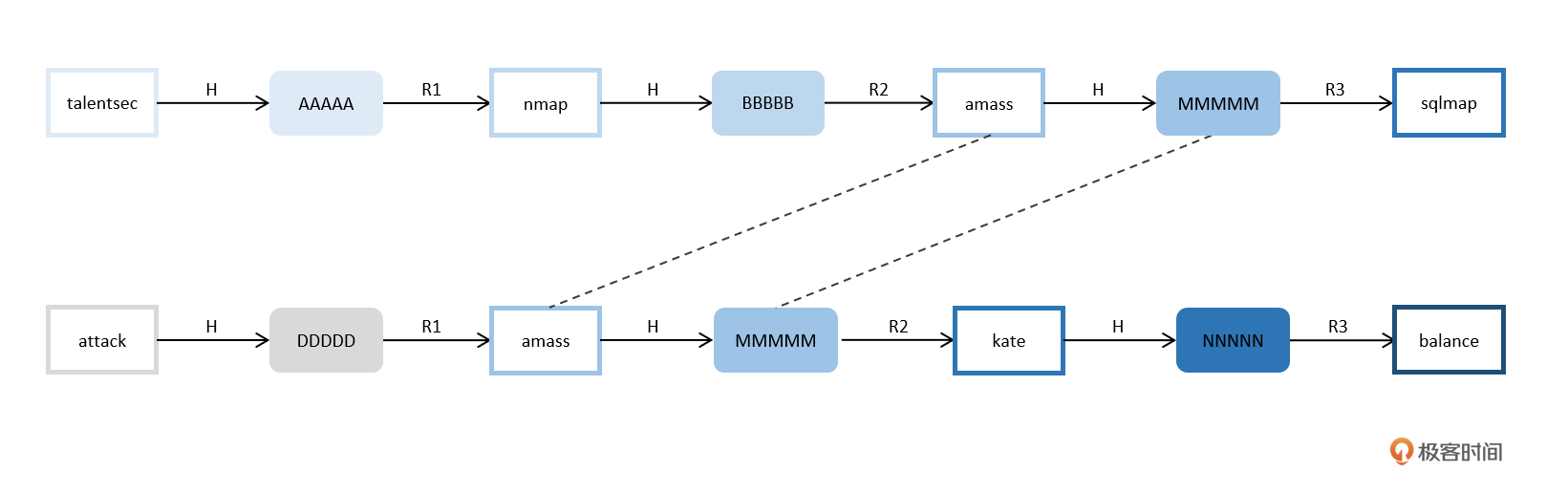
这样即使发生了之前我们所描述的碰撞情况,通常会是以下这种情况:
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
可以看到,虽然部分节点发生了碰撞,但是由于发生碰撞的位置并非在同一序列,使用的R函数也不是同一个,因此后续产生的节点也不相同。
|
|||
|
|
|
|||
|
|
这样,即使同一序列位置发生碰撞,导致后续节点完全相同,但是因为末节点是相同的,所以我们仍然可以非常快速地找出这条相似链,删除它来优化存储空间。
|
|||
|
|
|
|||
|
|
而关于彩虹表的使用方法,本质上与HASH链集并无二致,核心思想仍然是计算得出R函数的结果并与HASH链进行匹配。它们的区别在于,**计算出的序列结果是否唯一**。因为HASH链集使用的是相同的R函数,所以,如果我们对待破解的HASH散列进行R函数计算,所产生的序列结果是唯一的;但是彩虹表使用的是不同的R函数,因此计算时需要将待破解的HASH散列带入不同位置,从而得出多个序列结果。
|
|||
|
|
|
|||
|
|
## 案例实战
|
|||
|
|
|
|||
|
|
了解了彩虹表的原理和用法,接下来,我们就进入一个真实场景中实战一下。
|
|||
|
|
|
|||
|
|
打开[MiTuan](https://mituan.zone/#/)并选择【极客时间-漏洞挖掘与智能攻防实战】靶场,进入后选择【忘记加“盐”:加密结果强度不够吗?】靶机环境。
|
|||
|
|
|
|||
|
|
可以看到,这是一个很简单的登录界面。
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
接下来,我们使用简单的注入来获取用户密码信息:
|
|||
|
|
|
|||
|
|
```sql
|
|||
|
|
User = ' union select username,password from users;
|
|||
|
|
Password = 1
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
如果你不理解这个注入过程,不要担心,下一节课我们就会深入探讨SQL注入漏洞。
|
|||
|
|
通过简单的注入操作,我们可以获得用户名以及密码信息如下:
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
```plain
|
|||
|
|
Dumb
|
|||
|
|
2b161cb042f799e5f43ae6efc9e57926
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
接下来我们就尝试使用彩虹表攻击来破解这个HASH散列值。
|
|||
|
|
|
|||
|
|
首先解压我们提供的压缩包,进入rainbow目录后运行如下命令:
|
|||
|
|
|
|||
|
|
```bash
|
|||
|
|
docker build -t rainbow:v0 . # 构建镜像
|
|||
|
|
docker run -it rainbow:v0 # 启动容器并获得交互式shell
|
|||
|
|
|
|||
|
|
# 生成 md5哈希函数的 1-9a-zA-Z 最短1位 最长5位 10种不同R函数组合 每条链5000长度 10000条链 0偏移 的彩虹表
|
|||
|
|
./rtgen md5 mixalpha-numeric 1 5 10 10000 60000 0
|
|||
|
|
|
|||
|
|
# 生成彩虹表之后排序,方便结果查找
|
|||
|
|
./rtsort .
|
|||
|
|
|
|||
|
|
# 执行彩虹表破解,极小概率失败,主要是由于彩虹表具有不确定性,因此不能确保成功
|
|||
|
|
./rcrack . -h 2b161cb042f799e5f43ae6efc9e57926
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
在我的电脑上大约不到1秒就完成破解了,密码明文是`t1sec`,破解结果如下:
|
|||
|
|
|
|||
|
|
```bash
|
|||
|
|
1 rainbow tables found
|
|||
|
|
memory available: 1033964748 bytes
|
|||
|
|
memory for rainbow chain traverse: 160000 bytes per hash, 160000 bytes for 1 hashes
|
|||
|
|
memory for rainbow table buffer: 2 x 960016 bytes
|
|||
|
|
disk: ./md5_mixalpha-numeric#1-5_10_10000x60000_0.rt: 960000 bytes read
|
|||
|
|
disk: finished reading all files
|
|||
|
|
plaintext of 2b161cb042f799e5f43ae6efc9e57926 is t1sec
|
|||
|
|
|
|||
|
|
statistics
|
|||
|
|
----------------------------------------------------------------
|
|||
|
|
plaintext found: 1 of 1
|
|||
|
|
total time: 0.90 s
|
|||
|
|
time of chain traverse: 0.90 s
|
|||
|
|
time of alarm check: 0.00 s
|
|||
|
|
time of disk read: 0.00 s
|
|||
|
|
hash & reduce calculation of chain traverse: 49990000
|
|||
|
|
hash & reduce calculation of alarm check: 49990
|
|||
|
|
number of alarm: 257
|
|||
|
|
performance of chain traverse: 55.54 million/s
|
|||
|
|
performance of alarm check: 16.66 million/s
|
|||
|
|
|
|||
|
|
result
|
|||
|
|
----------------------------------------------------------------
|
|||
|
|
2b161cb042f799e5f43ae6efc9e57926 t1sec hex:7431736563
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
可以看到彩虹表的查询速度是非常快的,每秒可以执行约5500万条链的查询,实际上本次爆破仅使用了0.9s就已经攻击完成。
|
|||
|
|
|
|||
|
|
## 安全实践
|
|||
|
|
|
|||
|
|
好,学习了这么多,那么如何存储密码才是安全的呢?
|
|||
|
|
|
|||
|
|
安全级别从低到高,来看看我们都有哪些选择。
|
|||
|
|
|
|||
|
|
首先,最简单也是安全级别最低的方案,是**直接存储明文密码secret**,这种方式一旦系统遭遇攻击,会导致所有账户密码泄露,因此毫无安全性可言,在实际应用中已经被抛弃了。
|
|||
|
|
|
|||
|
|
接下来,目前一种常见的密码存储方案,就**是将明文密码带入一个HASH函数,并将散列值HASH(secret)作为结果存储到数据库**,使用这种方案,系统即使受到了入侵,攻击者获得的也只是HASH散列值。但是由于彩虹表的存在,密码依然很容易被破解。
|
|||
|
|
|
|||
|
|
更进一步地,我们可以**将明文密码加盐**,对加盐结果进行Hush运算HASH(secret+salt),然后将运算的散列值结果存储到数据库中。在保证每个用户的salt不一样的情况下,这种方案的安全性是可接受的,为了保证这一点,我们可以选择用户名、手机号等信息作为salt。
|
|||
|
|
|
|||
|
|
最后我们来看看,如何从**最佳安全实践**的角度处理数据。
|
|||
|
|
|
|||
|
|
一般来说,加盐会通过在原始字段的特定位置增加特定的字符,使其与原始输入不一致,比如用户使用了一个密码:
|
|||
|
|
|
|||
|
|
```plain
|
|||
|
|
talentsec
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
经过MD5处理后,可以得出结果:
|
|||
|
|
|
|||
|
|
```plain
|
|||
|
|
MD5 ("talentsec") = 0fd2671a7c179391e3e3ebb6ec70fa8f
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
很明显,该密码长度仅有9位,且完全使用小写英文字母。这样的密码取值空间很小,因此是很容易被彩虹表攻击的。因此,我们选择在用户的密码后添加特定的字符串,来增加它的安全性,比如新增用户的用户名:
|
|||
|
|
|
|||
|
|
```plain
|
|||
|
|
MD5 ("talentsecwwwhhhttt") = 91a9740ca090824cb00c4be0a319fb89
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
可以看到加盐之后密码位数变长了,同时散列结果也发生了变化。
|
|||
|
|
考虑到数据长度大幅增加,攻击者直接使用彩虹表攻击难度非常高。如果想要成功攻击散列值,攻击者则需要了解加盐的逻辑,并且以此逻辑重新生成彩虹表。即便如此,因为每个用户的加盐都是不一样的,攻击复杂度也只能针对单一密码降低,攻击者仍然无法使用彩虹表实现批量攻击,从结果上看,这将大大提高密码存储的安全性。
|
|||
|
|
|
|||
|
|
## 总结
|
|||
|
|
|
|||
|
|
回顾一下,这节课我们认识了一种系统开发中的调味品——“盐“。
|
|||
|
|
|
|||
|
|
首先,我们对“盐“是什么有了一个形象的认知,与做菜相似,**系统中通过使用“盐“(salt)来混淆输入**。而关于盐的使用,又不得不提HASH函数。作为一种特殊的密码学算法,**HASH函数具备计算不可逆、数据长度压缩、难以伪造等特性**,这些优秀的特性给它带来了非常多的应用场景,比如数据传递过程中的完整性校验、数据压缩与摘要、数据纠错与散列表等等。
|
|||
|
|
|
|||
|
|
正如人们由于烧菜时味道不够而生产了盐,在系统开发中,由于过去存储密码的方案安全性不足,因此引入了”盐“的概念。过去在系统中,普遍采用经过HASH函数运算的散列值来存储用户密码,这一过程面临的攻击主要包括暴力破解、字典攻击,但是这两种攻击方式因为在时间和空间上的损耗过高,所以难以真正实施。
|
|||
|
|
|
|||
|
|
彩虹表的出现打破了平静,它推翻了直接将用户密码运算出HASH散列值的方案,通过特殊设计的算法实现了时空平衡,这让攻击HASH散列值成为可能。
|
|||
|
|
|
|||
|
|
于是我们进一步分析了这种设计巧妙的攻击算法,验证了它对传统密码存储方案的威胁。而且我们不甘心于纸上谈兵,通过一个实战案例成功完成了一次彩虹表攻击。掌握了这种攻击方法,你就可以将它集成到自己的个性化智能攻击系统中。
|
|||
|
|
|
|||
|
|
最后,我们再次站在安全开发的角度,从目前普遍接受的安全实践出发,复现了最佳实践方案。
|
|||
|
|
|
|||
|
|
通过这节课的学习,相信你不仅掌握了HASH函数、盐、散列函数应用和安全最佳实践,还丰富了自己的智能攻击系统,使其功能更加强大。有了这些知识和装备的加持,相信你可以在安全领域进一步探索前行,发现更多二进制世界的秘密!
|
|||
|
|
|
|||
|
|
## 思考
|
|||
|
|
|
|||
|
|
在使用HASH链进行HASH散列值破解的过程中,如果原始输入与HASH链的头或者尾产生碰撞,为什么是很大可能性而不是一定在该链条中存在HASH散列值的破解结果呢?
|
|||
|
|
|
|||
|
|
欢迎在评论区留下你的思考,我们下节课再见。
|
|||
|
|
|
|||
|
|
相关工具:
|
|||
|
|
[https://github.com/talentsec/rainbow](https://github.com/talentsec/rainbow)
|
|||
|
|
|