352 lines
13 KiB
Markdown
352 lines
13 KiB
Markdown
|
|
# 13 | 如何通过有限向量空间加持的希尔密码,提高密码被破译的难度?
|
|||
|
|
|
|||
|
|
你好,我是朱维刚。欢迎你继续跟我学习线性代数。
|
|||
|
|
|
|||
|
|
今天我要讲的内容是“如何通过有限向量空间加持的希尔密码,提高密码被破译的难度”。
|
|||
|
|
|
|||
|
|
这篇的内容会非常有趣,是和密码加密、解密有关的。不知道你有没有看过电影《模仿游戏》,故事描述的是阿兰·图灵在二战期间破译德军的恩尼格玛密码机(Enigma),很精彩,我看了很多遍。
|
|||
|
|
|
|||
|
|

|
|||
|
|
|
|||
|
|
不过电影毕竟是电影,有许多内容是不现实的,好在表达出来的破译恩尼格玛密码的核心观点是正确的。要破译一份被恩尼格玛机加密的密文,需要这三类信息:
|
|||
|
|
|
|||
|
|
1. 恩格玛机的工作原理及内部构造,包括每个转子的线路连接;
|
|||
|
|
2. 德军对恩格玛机的操作守则;
|
|||
|
|
3. 德军所使用的每日初始设置。恩格玛机的每日初始设置包含了三个信息:即转子的排列顺序、每个转子的初始位置,以及插线板的设置。这些信息被印刷在密码本上分发至德军全军,每24小时更换一次设置,每月更换一次密码本。
|
|||
|
|
|
|||
|
|
这些在电影里确实都交代了,我也不过多剧透了。其实,恩尼格玛密码机的本质就是**替换密码**。而今天我要讲的也是一种替换密码——希尔密码。因为我们专栏讲的是线性代数,所以,这篇应用我们会以矩阵论原理为基础,来进行讲解。
|
|||
|
|
|
|||
|
|
## 为什么需要希尔密码?
|
|||
|
|
|
|||
|
|
要讲密码,我们得先知道人们为什么需要它。
|
|||
|
|
|
|||
|
|
最古老、最原始的加密算法,会把明文的字母按照某种配对关系替换成其他的字母,从而得到一段别人看不懂的密文,许多谍战剧用到过这类方法。看起来,这个方法好像很难人为进行破解,但从语言和统计学角度看,它其实是漏洞百出的。
|
|||
|
|
|
|||
|
|
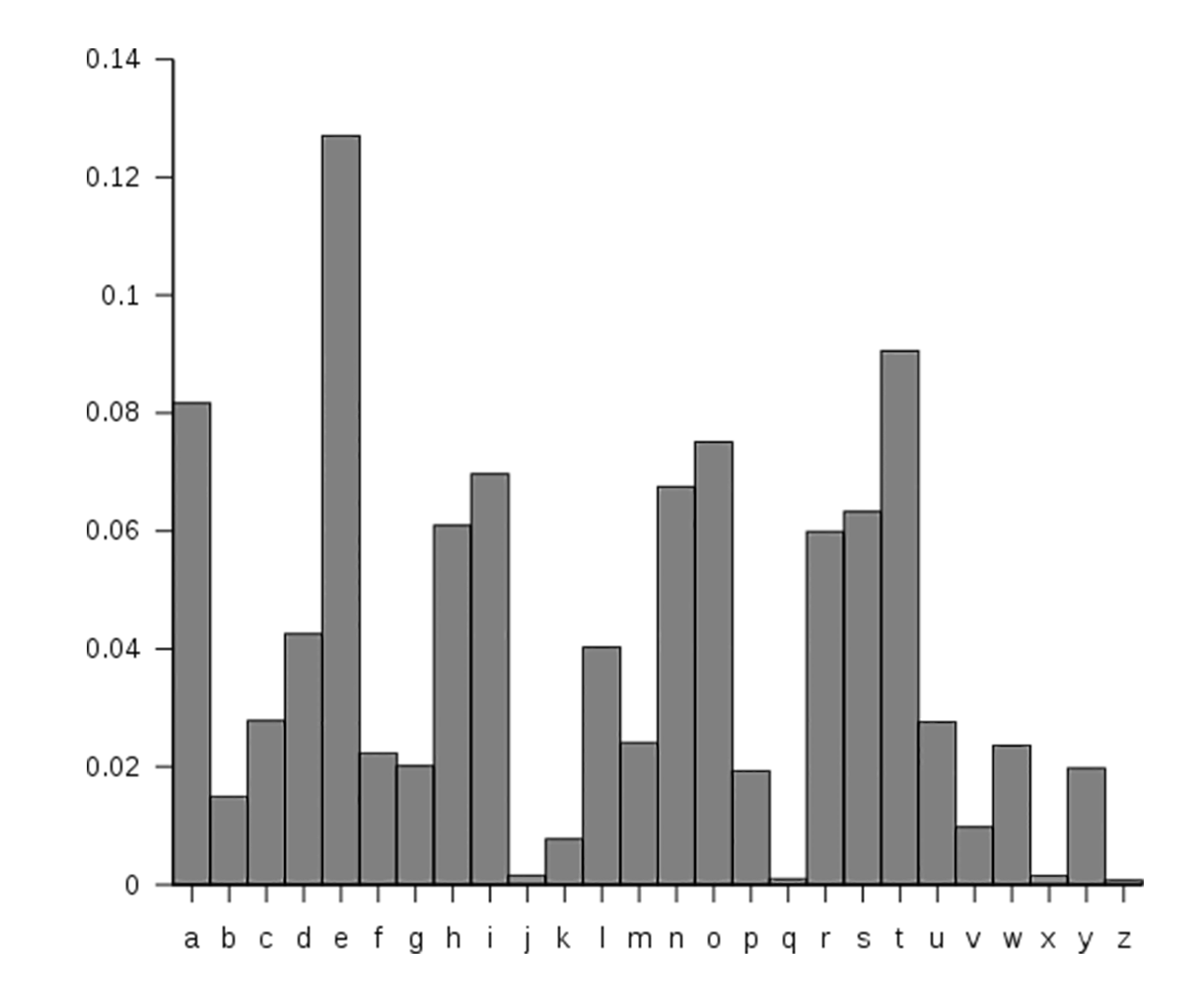
举个例子,在一篇普通英语文章中,各字母出现的概率有很大的不同。如果我们对足够多的文本进行分析,就可以统计出每一个字母在英文文本中出现的平均概率。
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
上面这张图来自维基百科,显示的是26个字母在普通的英文文本中出现的概率。
|
|||
|
|
|
|||
|
|
只要我们能够获取足够长的密文进行分析的话,通过字母出现的频率,我们同样能够猜到相应的原始字母,这并不安全。所以,随着安全性需求的提高,人们有必要寻找一种容易将字母的自然频度隐蔽或均匀化,并使得统计分析足够安全可靠的加密方法。而希尔密码能基本满足这一要求,那么希尔密码是怎么做到这一点的呢?
|
|||
|
|
|
|||
|
|
## 希尔密码原理
|
|||
|
|
|
|||
|
|
我们先来看一下希尔密码的原理。根据百度百科的定义,希尔密码(Hill Cipher)是运用基本矩阵论原理的替换密码,由Lester S. Hill在1929年发明。每个字母当作26进制数字:A=0,B=1,C=2… ,把一串字母当成$n$维向量,和一个$n×n$的矩阵相乘,再将得出的结果和26进行模运算。
|
|||
|
|
|
|||
|
|
所以,希尔加密算法的基本思想是,通过线性变换将固定数量的明文字母转换为同样数量的密文字母,解密只要作一次逆变换就可以了,而密钥就是变换矩阵本身。
|
|||
|
|
|
|||
|
|
现在,我们再通过数学的方式来表达一下,希尔密码是如何通过三步来实现加密的。
|
|||
|
|
|
|||
|
|
第一步,设置加密矩阵$E$。
|
|||
|
|
|
|||
|
|
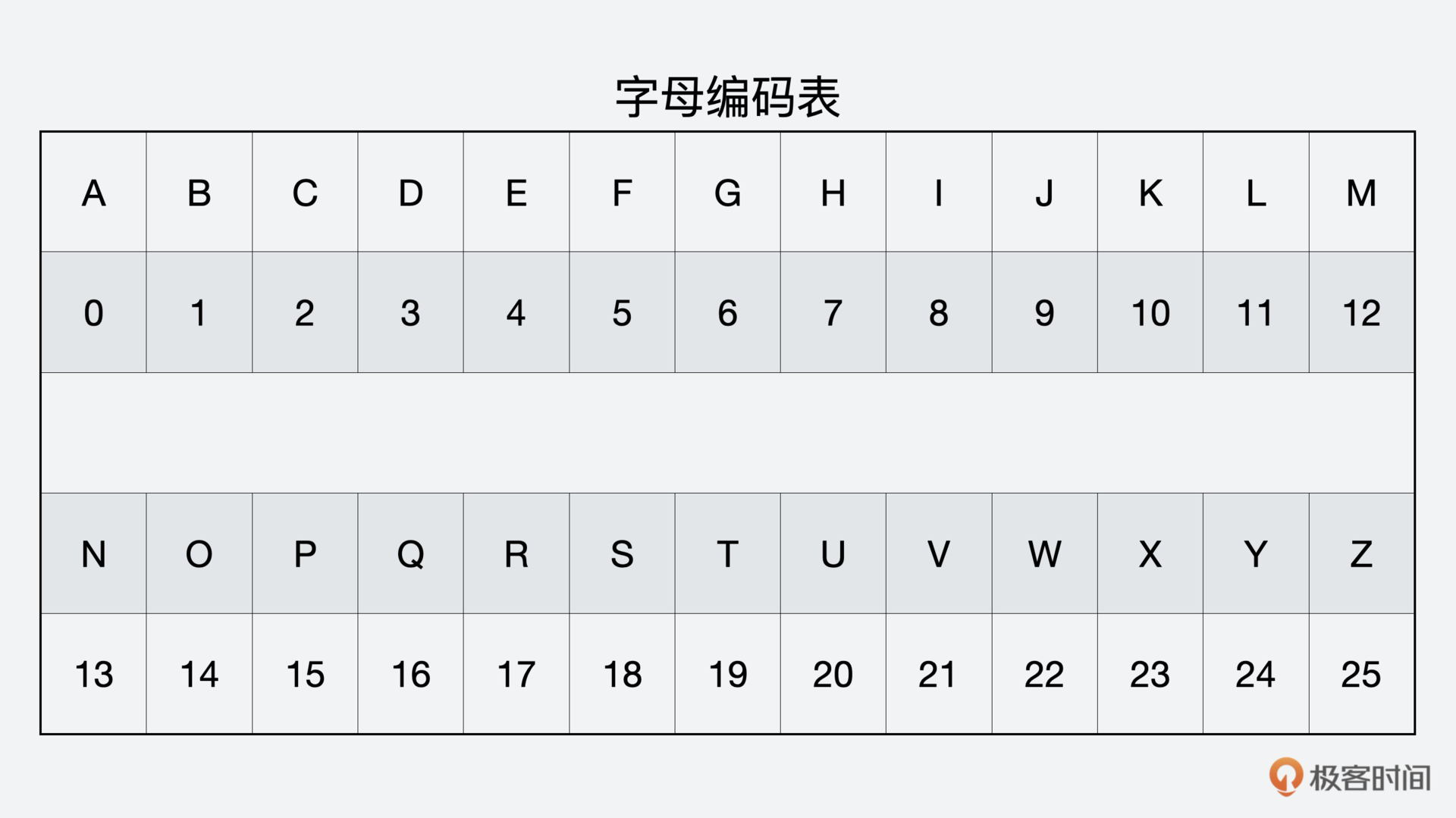
第二步,对照字母编码表(自行设定)得到数字,并把明文消息分割成大小为n的多个块:$v\_{1},v\_{2},…$,并且忽略空格。这里之所以忽略空格,是因为一般情况下密码传递的信息不会过于复杂。如果密码过于复杂,是可以分多次传递的。这里的n表示的密钥的阶数,密钥的阶数越高,也就是n越大的话,破译的难度也就越大,所需要的计算量也就越大。
|
|||
|
|
|
|||
|
|
第三步,每个消息块和加密矩阵$E$相乘:$Ev\_{1}, Ev\_{2},…$,并和26进行模运算,最后对照字母编码表得到密文。
|
|||
|
|
|
|||
|
|
同样,我们把这三步倒过来,就能实现解密了。
|
|||
|
|
|
|||
|
|
第一步,计算加密矩阵$E$的逆矩阵$D \\equiv E^{-1}(\\bmod 26)$。
|
|||
|
|
|
|||
|
|
第二步,对照字母编码表得到数字,把它和解密矩阵$D$相乘,并和26进行模运算。
|
|||
|
|
|
|||
|
|
第三步,对照编码表,得到原始明文。
|
|||
|
|
|
|||
|
|
这里你需要注意的是,加密矩阵很关键,它就是我们通常意义上所说的“密钥”,也就是打开密码的钥匙。
|
|||
|
|
|
|||
|
|
通过前面讲解的加密解密步骤,我们可以看出,希尔密码之所以很难被破译,是因为它设置了三道关卡:
|
|||
|
|
|
|||
|
|
1. 列矩阵的维度未知;
|
|||
|
|
2. 对应字母表的排列未知;
|
|||
|
|
3. 加密矩阵(或者说密钥)未知。
|
|||
|
|
|
|||
|
|
想要破解希尔密码,就需要同时获取到通过这三道关卡的钥匙,这谈何容易。
|
|||
|
|
|
|||
|
|
## 希尔密码实例
|
|||
|
|
|
|||
|
|
好了,原理都讲完了,现在我们通过一个例子来实际地看下希尔密码加密和解密的过程。
|
|||
|
|
|
|||
|
|
假设:A和B双方有一条重要消息要沟通,双方很早就建立了密钥沟通机制,每过一段时间都会更新密钥。在这次的密钥更新周期中,正确的密钥,也就是加密矩阵是一个3×3矩阵。
|
|||
|
|
|
|||
|
|
$$
|
|||
|
|
E=\\left\[\\begin{array}{ccc}
|
|||
|
|
6 & 24 & 1 \\\\\\
|
|||
|
|
13 & 16 & 10 \\\\\\
|
|||
|
|
20 & 17 & 15
|
|||
|
|
\\end{array}\\right\]
|
|||
|
|
$$
|
|||
|
|
|
|||
|
|
这一次A要给B的消息是“ILIKEBODYCOMBAT”,我们用之前的三步在A方先来加密:
|
|||
|
|
|
|||
|
|
第一步,定义加密矩阵,也就是刚才的$E$矩阵。
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
第二步,对照字母编码表得到数字:8、11、8、10、4、1、14、3、24、2、14、12、1、0、19。接下来,把明文消息分割成大小为3的5个块,也就是维度为3的5个列矩阵。
|
|||
|
|
|
|||
|
|
$$
|
|||
|
|
v\_{1}=\\left\[\\begin{array}{c}
|
|||
|
|
8 \\\\\\
|
|||
|
|
11 \\\\\\
|
|||
|
|
8
|
|||
|
|
\\end{array}\\right\], v\_{2}=\\left\[\\begin{array}{c}
|
|||
|
|
10 \\\\\\
|
|||
|
|
4 \\\\\\
|
|||
|
|
1
|
|||
|
|
\\end{array}\\right\], v\_{3}=\\left\[\\begin{array}{c}
|
|||
|
|
14 \\\\\\
|
|||
|
|
3 \\\\\\
|
|||
|
|
24
|
|||
|
|
\\end{array}\\right\], v\_{4}=\\left\[\\begin{array}{c}
|
|||
|
|
2 \\\\\\
|
|||
|
|
14 \\\\\\
|
|||
|
|
12
|
|||
|
|
\\end{array}\\right\], v\_{5}=\\left\[\\begin{array}{c}
|
|||
|
|
1 \\\\\\
|
|||
|
|
0 \\\\\\
|
|||
|
|
19
|
|||
|
|
\\end{array}\\right\]
|
|||
|
|
$$
|
|||
|
|
|
|||
|
|
第三步,将每个消息块和加密矩阵$E$相乘:
|
|||
|
|
|
|||
|
|
$$
|
|||
|
|
E v\_{1}=\\left\[\\begin{array}{ccc}
|
|||
|
|
6 & 24 & 1 \\\\\\
|
|||
|
|
13 & 16 & 10 \\\\\\
|
|||
|
|
20 & 17 & 15
|
|||
|
|
\\end{array}\\right\]\\left\[\\begin{array}{c}
|
|||
|
|
8 \\\\\\
|
|||
|
|
11 \\\\\\
|
|||
|
|
8
|
|||
|
|
\\end{array}\\right\]=\\left\[\\begin{array}{c}
|
|||
|
|
320 \\\\\\
|
|||
|
|
360 \\\\\\
|
|||
|
|
467
|
|||
|
|
\\end{array}\\right\] \\bmod 26=\\left\[\\begin{array}{c}
|
|||
|
|
8 \\\\\\
|
|||
|
|
22 \\\\\\
|
|||
|
|
25
|
|||
|
|
\\end{array}\\right\]
|
|||
|
|
$$
|
|||
|
|
|
|||
|
|
$$
|
|||
|
|
E v\_{2}=\\left\[\\begin{array}{ccc}
|
|||
|
|
6 & 24 & 1 \\\\\\
|
|||
|
|
13 & 16 & 10 \\\\\\
|
|||
|
|
20 & 17 & 15
|
|||
|
|
\\end{array}\\right\]\\left\[\\begin{array}{c}
|
|||
|
|
10 \\\\\\
|
|||
|
|
4 \\\\\\
|
|||
|
|
1
|
|||
|
|
\\end{array}\\right\]=\\left\[\\begin{array}{c}
|
|||
|
|
157 \\\\\\
|
|||
|
|
204 \\\\\\
|
|||
|
|
283
|
|||
|
|
\\end{array}\\right\] \\bmod 26=\\left\[\\begin{array}{c}
|
|||
|
|
1 \\\\\\
|
|||
|
|
22 \\\\\\
|
|||
|
|
23
|
|||
|
|
\\end{array}\\right\]
|
|||
|
|
$$
|
|||
|
|
|
|||
|
|
$$
|
|||
|
|
E v\_{3}=\\left\[\\begin{array}{ccc}
|
|||
|
|
6 & 24 & 1 \\\\\\
|
|||
|
|
13 & 16 & 10 \\\\\\
|
|||
|
|
20 & 17 & 15
|
|||
|
|
\\end{array}\\right\]\\left\[\\begin{array}{c}
|
|||
|
|
14 \\\\\\
|
|||
|
|
3 \\\\\\
|
|||
|
|
24
|
|||
|
|
\\end{array}\\right\]=\\left\[\\begin{array}{c}
|
|||
|
|
180 \\\\\\
|
|||
|
|
470 \\\\\\
|
|||
|
|
691
|
|||
|
|
\\end{array}\\right\] \\bmod 26=\\left\[\\begin{array}{c}
|
|||
|
|
24 \\\\\\
|
|||
|
|
2 \\\\\\
|
|||
|
|
15
|
|||
|
|
\\end{array}\\right\]
|
|||
|
|
$$
|
|||
|
|
|
|||
|
|
$$
|
|||
|
|
E v\_{4}=\\left\[\\begin{array}{ccc}
|
|||
|
|
6 & 24 & 1 \\\\\\
|
|||
|
|
13 & 16 & 10 \\\\\\
|
|||
|
|
20 & 17 & 15
|
|||
|
|
\\end{array}\\right\]\\left\[\\begin{array}{c}
|
|||
|
|
2 \\\\\\
|
|||
|
|
14 \\\\\\
|
|||
|
|
12
|
|||
|
|
\\end{array}\\right\]=\\left\[\\begin{array}{c}
|
|||
|
|
360 \\\\\\
|
|||
|
|
370 \\\\\\
|
|||
|
|
458
|
|||
|
|
\\end{array}\\right\] \\bmod 26=\\left\[\\begin{array}{c}
|
|||
|
|
22 \\\\\\
|
|||
|
|
6 \\\\\\
|
|||
|
|
16
|
|||
|
|
\\end{array}\\right\]
|
|||
|
|
$$
|
|||
|
|
|
|||
|
|
$$
|
|||
|
|
E v\_{5}=\\left\[\\begin{array}{ccc}
|
|||
|
|
6 & 24 & 1 \\\\\\
|
|||
|
|
13 & 16 & 10 \\\\\\
|
|||
|
|
20 & 17 & 15
|
|||
|
|
\\end{array}\\right\]\\left\[\\begin{array}{c}
|
|||
|
|
1 \\\\\\
|
|||
|
|
0 \\\\\\
|
|||
|
|
19
|
|||
|
|
\\end{array}\\right\]=\\left\[\\begin{array}{c}
|
|||
|
|
25 \\\\\\
|
|||
|
|
203 \\\\\\
|
|||
|
|
305
|
|||
|
|
\\end{array}\\right\] \\bmod 26=\\left\[\\begin{array}{c}
|
|||
|
|
25 \\\\\\
|
|||
|
|
21 \\\\\\
|
|||
|
|
19
|
|||
|
|
\\end{array}\\right\]
|
|||
|
|
$$
|
|||
|
|
|
|||
|
|
最后,对照字母编码表得到密文:“IWZBWXBCGWGQZVT”。
|
|||
|
|
|
|||
|
|
B拿到这个密文后,使用三步来解密:
|
|||
|
|
|
|||
|
|
第一步,计算加密矩阵E的逆矩阵$D$:
|
|||
|
|
|
|||
|
|
$$
|
|||
|
|
D \\equiv\\left\[\\begin{array}{ccc}
|
|||
|
|
6 & 24 & 1 \\\\\\
|
|||
|
|
13 & 16 & 10 \\\\\\
|
|||
|
|
20 & 17 & 15
|
|||
|
|
\\end{array}\\right\]^{-1}(\\bmod 26) \\equiv\\left\[\\begin{array}{ccc}
|
|||
|
|
8 & 5 & 10 \\\\\\
|
|||
|
|
21 & 8 & 21 \\\\\\
|
|||
|
|
21 & 12 & 8
|
|||
|
|
\\end{array}\\right\]
|
|||
|
|
$$
|
|||
|
|
|
|||
|
|
第二步,对照字母编码表得到数字,把它和解密矩阵D相乘,并和26进行模运算,得到相应结果。
|
|||
|
|
|
|||
|
|
$$
|
|||
|
|
\\left\[\\begin{array}{ccc}
|
|||
|
|
8 & 5 & 10 \\\\\\
|
|||
|
|
21 & 8 & 21 \\\\\\
|
|||
|
|
21 & 12 & 8
|
|||
|
|
\\end{array}\\right\]\\left\[\\begin{array}{c}
|
|||
|
|
8 \\\\\\
|
|||
|
|
22 \\\\\\
|
|||
|
|
25
|
|||
|
|
\\end{array}\\right\]=\\left\[\\begin{array}{c}
|
|||
|
|
424 \\\\\\
|
|||
|
|
869 \\\\\\
|
|||
|
|
632
|
|||
|
|
\\end{array}\\right\] \\bmod 26=\\left\[\\begin{array}{c}
|
|||
|
|
8 \\\\\\
|
|||
|
|
11 \\\\\\
|
|||
|
|
8
|
|||
|
|
\\end{array}\\right\]
|
|||
|
|
$$
|
|||
|
|
|
|||
|
|
$$
|
|||
|
|
\\left\[\\begin{array}{ccc}
|
|||
|
|
8 & 5 & 10 \\\\\\
|
|||
|
|
21 & 8 & 21 \\\\\\
|
|||
|
|
21 & 12 & 8
|
|||
|
|
\\end{array}\\right\]\\left\[\\begin{array}{c}
|
|||
|
|
1 \\\\\\
|
|||
|
|
22 \\\\\\
|
|||
|
|
23
|
|||
|
|
\\end{array}\\right\]=\\left\[\\begin{array}{c}
|
|||
|
|
348 \\\\\\
|
|||
|
|
680 \\\\\\
|
|||
|
|
469
|
|||
|
|
\\end{array}\\right\] \\bmod 26=\\left\[\\begin{array}{c}
|
|||
|
|
10 \\\\\\
|
|||
|
|
4 \\\\\\
|
|||
|
|
1
|
|||
|
|
\\end{array}\\right\]
|
|||
|
|
$$
|
|||
|
|
|
|||
|
|
$$
|
|||
|
|
\\left\[\\begin{array}{ccc}
|
|||
|
|
8 & 5 & 10 \\\\\\
|
|||
|
|
21 & 8 & 21 \\\\\\
|
|||
|
|
21 & 12 & 8
|
|||
|
|
\\end{array}\\right\]\\left\[\\begin{array}{c}
|
|||
|
|
24 \\\\\\
|
|||
|
|
2 \\\\\\
|
|||
|
|
15
|
|||
|
|
\\end{array}\\right\]=\\left\[\\begin{array}{c}
|
|||
|
|
352 \\\\\\
|
|||
|
|
835 \\\\\\
|
|||
|
|
648
|
|||
|
|
\\end{array}\\right\] \\bmod 26=\\left\[\\begin{array}{c}
|
|||
|
|
14 \\\\\\
|
|||
|
|
3 \\\\\\
|
|||
|
|
24
|
|||
|
|
\\end{array}\\right\]
|
|||
|
|
$$
|
|||
|
|
|
|||
|
|
$$
|
|||
|
|
\\left\[\\begin{array}{ccc}
|
|||
|
|
8 & 5 & 10 \\\\\\
|
|||
|
|
21 & 8 & 21 \\\\\\
|
|||
|
|
21 & 12 & 8
|
|||
|
|
\\end{array}\\right\]\\left\[\\begin{array}{c}
|
|||
|
|
22 \\\\\\
|
|||
|
|
6 \\\\\\
|
|||
|
|
16
|
|||
|
|
\\end{array}\\right\]=\\left\[\\begin{array}{c}
|
|||
|
|
366 \\\\\\
|
|||
|
|
846 \\\\\\
|
|||
|
|
662
|
|||
|
|
\\end{array}\\right\] \\bmod 26=\\left\[\\begin{array}{c}
|
|||
|
|
2 \\\\\\
|
|||
|
|
14 \\\\\\
|
|||
|
|
12
|
|||
|
|
\\end{array}\\right\]
|
|||
|
|
$$
|
|||
|
|
|
|||
|
|
$$
|
|||
|
|
\\left\[\\begin{array}{ccc}
|
|||
|
|
8 & 5 & 10 \\\\\\
|
|||
|
|
21 & 8 & 21 \\\\\\
|
|||
|
|
21 & 12 & 8
|
|||
|
|
\\end{array}\\right\]\\left\[\\begin{array}{c}
|
|||
|
|
25 \\\\\\
|
|||
|
|
21 \\\\\\
|
|||
|
|
19
|
|||
|
|
\\end{array}\\right\]=\\left\[\\begin{array}{c}
|
|||
|
|
495 \\\\\\
|
|||
|
|
1092 \\\\\\
|
|||
|
|
929
|
|||
|
|
\\end{array}\\right\] \\bmod 26=\\left\[\\begin{array}{c}
|
|||
|
|
1 \\\\\\
|
|||
|
|
0 \\\\\\
|
|||
|
|
19
|
|||
|
|
\\end{array}\\right\]
|
|||
|
|
$$
|
|||
|
|
|
|||
|
|
最后,B通过对照编码表,得到了原始明文:“ILIKEBODYCOMBAT”。
|
|||
|
|
|
|||
|
|
这里,你也许会问,密钥为什么用的是3×3的可逆矩阵?那是我为了例子方便而设置的,你完全可以设置更高阶的矩阵。就像之前说的,密钥的阶数越高,也就是$n$越大的话,破译的难度也就越大,所需要的计算量也就越大。
|
|||
|
|
|
|||
|
|
所以,从破译密码的角度来看,传统的密码有一个致命弱点,就是破译者可从统计出来的字符频率中找到规律,进而找出破译的突破口。尤其是在计算机技术高度发达的今天,破译的速度更快。而希尔密码算法则完全克服了这一缺陷,它通过采用线性代数中的矩阵乘法运算和逆运算,能够较好地抵抗频率分析,很难被攻破。
|
|||
|
|
|
|||
|
|
## 本节小结
|
|||
|
|
|
|||
|
|
这一节课的内容都和密码学有关,感觉像是搞谍战一样。但其实它的核心很简单,就是通过基础篇中学到的矩阵和逆矩阵的知识,来实现希尔密码。希尔密码的关键就是定义加密矩阵,或者说密钥、字母表排列方式和列矩阵的维度,通过线性变换将固定数量的明文字母转换为同样数量的密文字母,而解密则只要作一次逆变换就可以了。
|
|||
|
|
|
|||
|
|
当然,现实中还有更复杂的加密算法,其中最著名的,且用到线性代数的加密算法是AES,想必你平时也经常看到或用到过。AES是一个迭代的、对称密钥分组的密码,它可以使用128、192和256位密钥,并且用128、192和256位分组加密和解密数据,其中密钥长度与分组长度是独立的。
|
|||
|
|
|
|||
|
|
## 线性代数练习场
|
|||
|
|
|
|||
|
|
请你做一回“特工”,尝试使用希尔密码来给明文“MACHINELEARNING”做加密和解密。
|
|||
|
|
|
|||
|
|
> 提醒:你可以自行定义加密矩阵、字母表排列方式和列矩阵的维度。加密矩阵可以使用之前介绍的3×3可逆矩阵,也可以使用其它n×n的可逆矩阵。
|
|||
|
|
|
|||
|
|
欢迎在留言区晒出你的加密和解密过程,我会及时回复。同时,也欢迎你把这篇文章分享给你的朋友,一起讨论、学习。
|
|||
|
|
|