195 lines
11 KiB
Markdown
195 lines
11 KiB
Markdown
|
|
# 41 | 线性回归(下):如何使用最小二乘法进行效果验证?
|
|||
|
|
|
|||
|
|
你好,我是黄申。
|
|||
|
|
|
|||
|
|
上一节我们已经解释了最小二乘法的核心思想和具体推导过程。今天我们就用实际的数据操练一下,这样你的印象就会更加深刻。我会使用几个具体的例子,演示一下如何使用最小二乘法的结论,通过观测到的自变量和因变量值,来推算系数,并使用这个系数来进行新的预测。
|
|||
|
|
|
|||
|
|
## 基于最小二乘法的求解
|
|||
|
|
|
|||
|
|
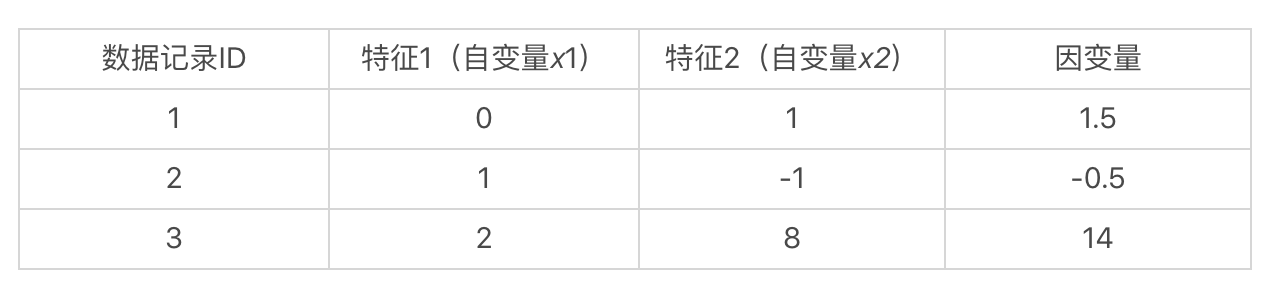
假想我们手头上有一个数据集,里面有3条数据记录。每条数据记录有2维特征,也就是2个自变量,和1个因变量。
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
如果我们假设这些自变量和因变量都是线性的关系,那么我们就可以使用如下这种线性方程,来表示数据集中的样本:
|
|||
|
|
|
|||
|
|
$b\_1·0+b\_2·1=1.5$
|
|||
|
|
$b\_1·1-b\_2·1=-0.5$
|
|||
|
|
$b\_1·2+b\_2·8=14$
|
|||
|
|
|
|||
|
|
也就是说,我们通过观察数据已知了自变量$x\_1$、$x\_2$和因变量$y$的值,而要求解的是$b\_1$和$b\_2$这两个系数。如果我们能求出$b\_1$和$b\_2$,那么在处理新数据的时候,就能根据新的自变量$x\_1$和$x\_2$的取值,来预测$y$的值。
|
|||
|
|
|
|||
|
|
可是我们说过,由实际项目中的数据集所构成的这类方程组,在绝大多数情况下,都没有精确解。所以这个时候我们没法使用之前介绍的高斯消元法,而是要考虑最小二乘法。根据上一节的结论,我们知道对于系数矩阵$B$,有:
|
|||
|
|
|
|||
|
|
$B=(X’X)^{-1}X’Y$
|
|||
|
|
|
|||
|
|
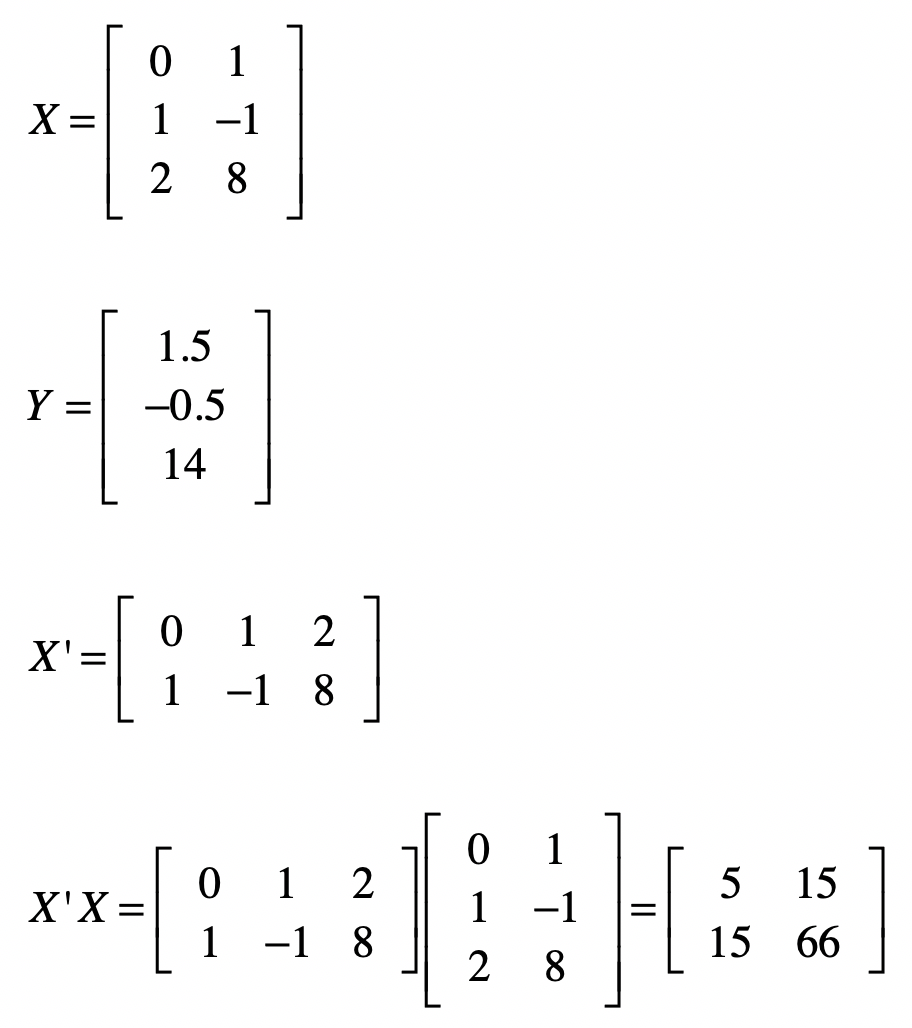
既然有了这个公式,要求$B$就不难了,让我们从最基本的几个矩阵开始。
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
矩阵$(X’X)^{-1}$的求解稍微繁琐一点。逆矩阵的求法我还没讲解过,之前我们说过线性方程组之中,高斯消元和回代的过程,就是把系数矩阵变为单位矩阵的过程。我们可以利用这点,来求解$X^{-1}$。我们把原始的系数矩阵$X$列在左边,然后把单位矩阵列在右边,像$\[X | I\]$这种形式,其中$I$表示单位矩阵。
|
|||
|
|
|
|||
|
|
然后我们对左侧的矩阵进行高斯消元和回代,把左边矩阵X变为单位矩阵。同时,我们也把这个相应的矩阵操作运用在右侧。这样当左侧变为单位矩阵之后,那么右侧的矩阵就是原始矩阵$X$的逆矩阵$X^{-1}$,具体证明如下:
|
|||
|
|
|
|||
|
|
$\[X | I\]$
|
|||
|
|
$\[X^{-1}X | X^{-1}I\]$
|
|||
|
|
$\[I | X^{-1}I\]$
|
|||
|
|
$\[I | X^{-1}\]$
|
|||
|
|
|
|||
|
|
好了,给定下面的$X’X$矩阵之后,我们使用上述方法来求$(X’X)^{-1}$ 。我把具体的推导过程列在了这里。
|
|||
|
|
|
|||
|
|
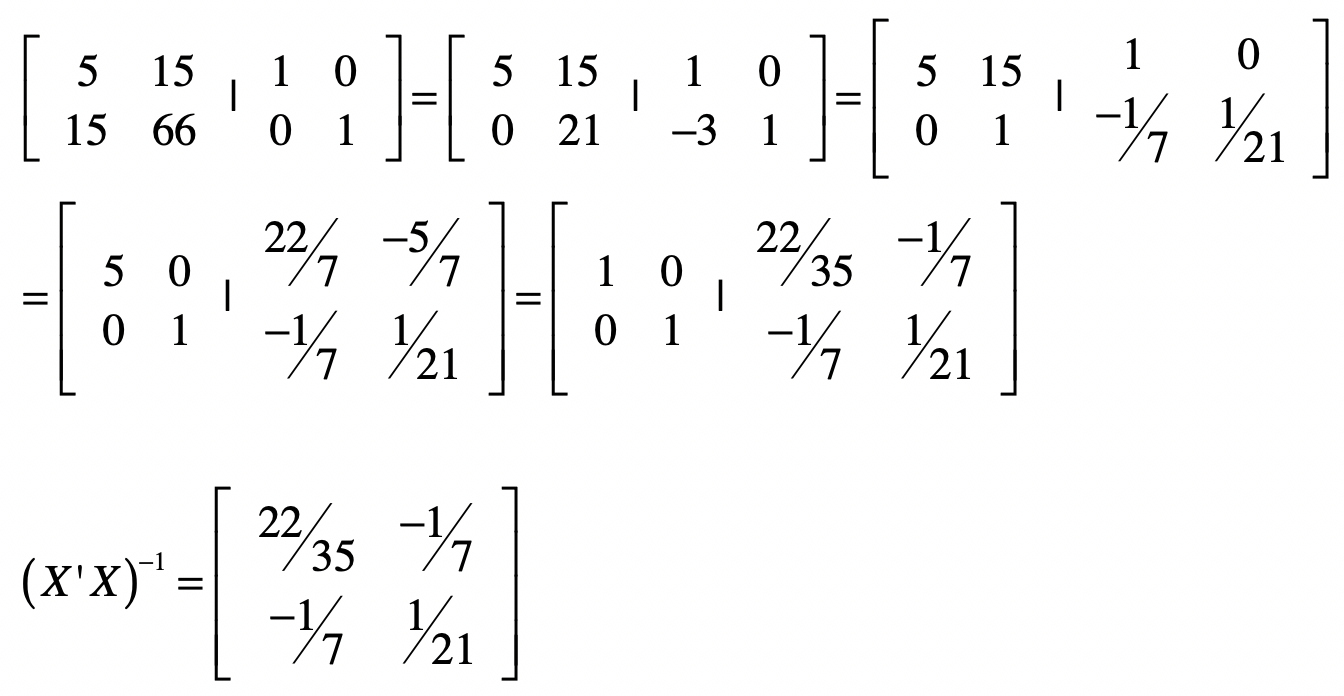
|
|||
|
|
|
|||
|
|
求出$(X’X)^{-1}$之后,我们就可以使用$B=(X’X)^{-1}X’Y$来计算矩阵B。
|
|||
|
|
|
|||
|
|
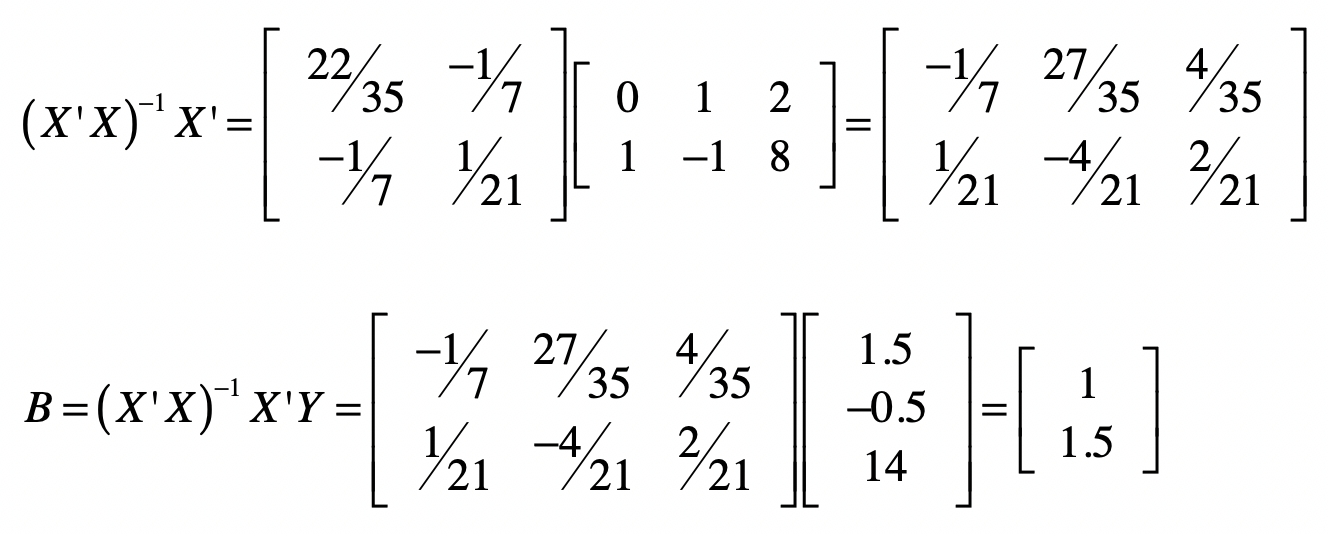
|
|||
|
|
|
|||
|
|
最终,我们求出系数矩阵为$\[1 1.5\]$,也就是说$b\_1 = 1$, $b\_2 = 1.5$。实际上,这两个数值是精确解。我们用高斯消元也是能获得同样结果的。接下来,让我稍微修改一下$y$值,让这个方程组没有精确解。
|
|||
|
|
|
|||
|
|
$b\_1·0+b\_2·1=1.4$
|
|||
|
|
$b\_1·1-b\_2·1=-0.48$
|
|||
|
|
$b\_1·2+b\_2·8=13.2$
|
|||
|
|
|
|||
|
|
你可以尝试高斯消元法对这个方程组求解,你会发现只要两个方程就能求出解,但是无论是哪两个方程求出的解,都无法满足第三个方程。
|
|||
|
|
|
|||
|
|
那么通过最小二乘法,我们能不能求导一个近似解,保证\_ε\_足够小呢?下面,让我们遵循之前求解$(X’X)^{-1}X’Y$的过程,来计算$B$。
|
|||
|
|
|
|||
|
|
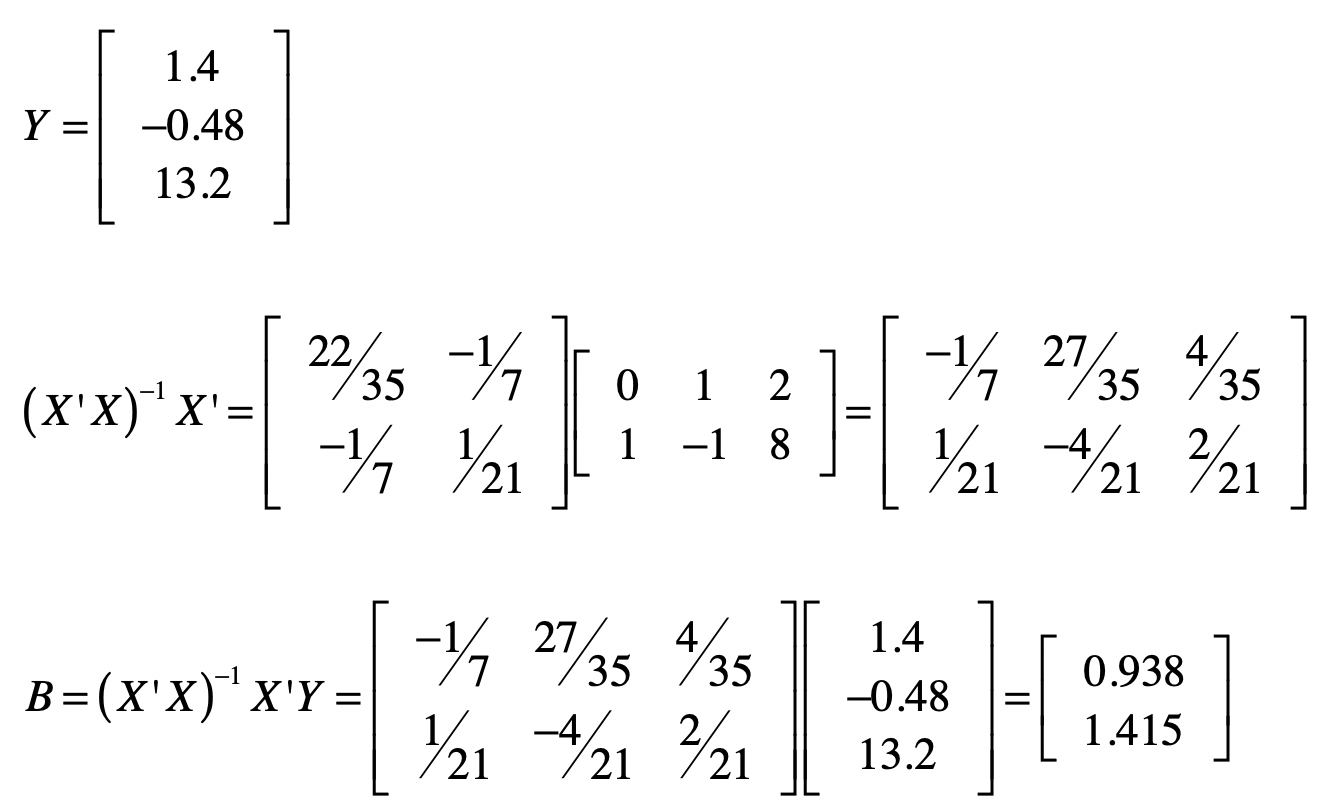
|
|||
|
|
|
|||
|
|
计算完毕之后,你会发现两个系数的值分别变为$b\_1 = 0.938, b\_2 = 1.415$。由于这不是精确解,所以让我们看看有了这系数矩阵$B$之后,原有的观测数据中,真实值和预测值的差别。
|
|||
|
|
|
|||
|
|
首先我们通过系数矩阵$B$和自变量矩阵$X$计算出来预测值。
|
|||
|
|
|
|||
|
|
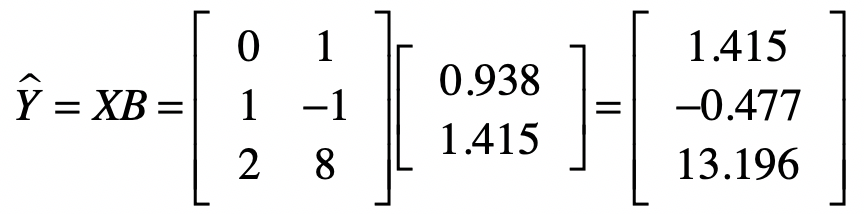
|
|||
|
|
|
|||
|
|
然后是样本数据中的观测值。这里我们假设这些值是真实值。
|
|||
|
|
|
|||
|
|
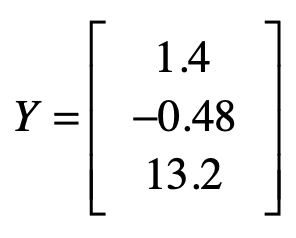
|
|||
|
|
|
|||
|
|
根据误差$ε$的定义,我们可以得到:
|
|||
|
|
|
|||
|
|
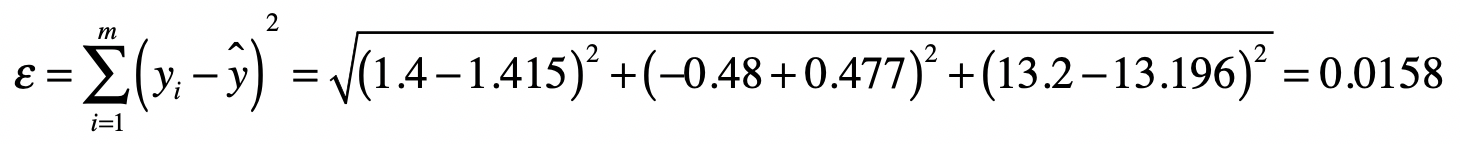
|
|||
|
|
|
|||
|
|
说到这里,你可能会怀疑,通过最小二乘法所求得的系数$b\_1 = 0.949$和$b\_2 = 1.415$,是不是能让$ε$最小呢?这里,我们随机的修改一下这两个系数,变为$b\_1 = 0.95$和$b\_2 = 1.42$,然后我们再次计算预测的$y$值和$ε$。
|
|||
|
|
|
|||
|
|
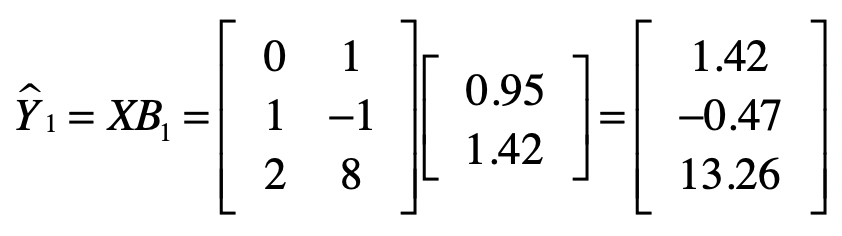
|
|||
|
|
|
|||
|
|
很明显,0.064是大于之前的0.0158。
|
|||
|
|
|
|||
|
|
这两次计算预测值\_y\_的过程,其实也是我们使用线性回归,对新的数据进行预测的过程。简短地总结一下,线性回归模型根据大量的训练样本,推算出系数矩阵$B$,然后根据新数据的自变量$X$向量或者矩阵,计算出因变量的值,作为新数据的预测。
|
|||
|
|
|
|||
|
|
## Python代码实现
|
|||
|
|
|
|||
|
|
这一部分,我们使用Python的代码,来验证一下之前的推算结果是不是正确,并看看最小二乘法和Python sklearn库中的线性回归,这两种结果的对比。
|
|||
|
|
|
|||
|
|
首先,我们使用Python numpy库中的矩阵操作来实现最小二乘法。主要的函数操作涉及矩阵的转置、点乘和求逆。具体的代码和注释我列在了下方。
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
from numpy import *
|
|||
|
|
|
|||
|
|
x = mat([[0,1],[1,-1],[2,8]])
|
|||
|
|
y = mat([[1.4],[-0.48],[13.2]])
|
|||
|
|
|
|||
|
|
# 分别求出矩阵X'、X'X、(X'X)的逆
|
|||
|
|
# 注意,这里的I表示逆矩阵而不是单位矩阵
|
|||
|
|
print("X矩阵的转置X':\n", x.transpose())
|
|||
|
|
print("\nX'点乘X:\n", x.transpose().dot(x))
|
|||
|
|
print("\nX'X矩阵的逆\n", (x.transpose().dot(x)).I)
|
|||
|
|
|
|||
|
|
print("\nX'X矩阵的逆点乘X'\n", (x.transpose().dot(x)).I.dot(x.transpose()))
|
|||
|
|
print("\n系数矩阵B:\n", (x.transpose().dot(x)).I.dot(x.transpose()).dot(y))
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
通过上述代码,你可以看到每一步的结果,以及最终的矩阵$B$。你可以把输出结果和之前手动推算的结果进行对比,看看是不是一致。
|
|||
|
|
|
|||
|
|
除此之外,我们还可把最小二乘法的线性拟合结果和sklearn库中的LinearRegression().fit()函数的结果相比较,具体的代码和注释我也放在了这里。
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
import pandas as pd
|
|||
|
|
from sklearn.linear_model import LinearRegression
|
|||
|
|
|
|||
|
|
df = pd.read_csv("/Users/shenhuang/Data/test.csv")
|
|||
|
|
df_features = df.drop(['y'], axis=1) #Dataframe中除了最后一列,其余列都是特征,或者说自变量
|
|||
|
|
df_targets = df['y'] #Dataframe最后一列是目标变量,或者说因变量
|
|||
|
|
|
|||
|
|
print(df_features, df_targets)
|
|||
|
|
regression = LinearRegression().fit(df_features, df_targets) #使用特征和目标数据,拟合线性回归模型
|
|||
|
|
print(regression.score(df_features, df_targets)) #拟合程度的好坏
|
|||
|
|
print(regression.intercept_)
|
|||
|
|
print(regression.coef_) #各个特征所对应的系数
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
其中,test.csv文件的内容我也列在了这里。
|
|||
|
|
|
|||
|
|
$x\_1,x\_2,y$
|
|||
|
|
$0,1,1.4$
|
|||
|
|
$1,-1,-0.48$
|
|||
|
|
$2,8,13.2$
|
|||
|
|
|
|||
|
|
这样写是为了方便我们使用pandas读取csv文件并加载为dataframe。
|
|||
|
|
|
|||
|
|
在最终的结果中,1.0表示拟合程度非常好,而-0.014545454545452863表示一个截距,\[0.94909091 1.41454545\]表示系数$b\_1$和$b\_2$的值。这个结果和我们最小二乘法的结果有所差别,主要原因是LinearRegression().fit()默认考虑了有线性函数存在截距的情况。那么我们使用最小二乘法是不是也可以考虑有截距的情况呢?答案是肯定的,不过我们首先要略微修改一下方程组和矩阵$X$。如果我们假设有截距存在,那么线性回归方程就要改写为:
|
|||
|
|
|
|||
|
|
$b\_0+b\_1·x\_1+b\_2·x\_2+…+b\_{n-1}·x\_{n-1}+b\_n·x\_n=y$
|
|||
|
|
|
|||
|
|
其中,$b\_0$表示截距,而我们这里的方程组用例就要改写为:
|
|||
|
|
|
|||
|
|
$b\_0+b\_1·0+b\_2·1=1.4$
|
|||
|
|
$b\_0+b\_1·1-b\_2·1=-0.48$
|
|||
|
|
$b\_0+b\_1·2+b\_2·8=13.2$
|
|||
|
|
|
|||
|
|
而矩阵$X$要改写为:
|
|||
|
|
|
|||
|
|
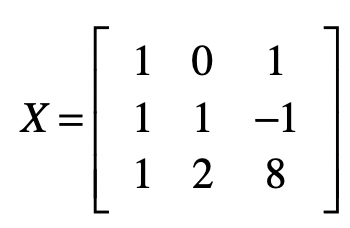
|
|||
|
|
|
|||
|
|
然后我们再执行下面这段代码。
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
from numpy import *
|
|||
|
|
|
|||
|
|
x = mat([[1,0,1],[1,1,-1],[1,2,8]])
|
|||
|
|
y = mat([[1.4],[-0.48],[13.2]])
|
|||
|
|
|
|||
|
|
print("\n系数矩阵B:\n", (x.transpose().dot(x)).I.dot(x.transpose()).dot(y))
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
你就会得到:
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
系数矩阵B:
|
|||
|
|
[[-0.01454545]
|
|||
|
|
[ 0.94909091]
|
|||
|
|
[ 1.41454545]]
|
|||
|
|
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
这个结果和LinearRegression().fit()的结果就一致了。
|
|||
|
|
|
|||
|
|
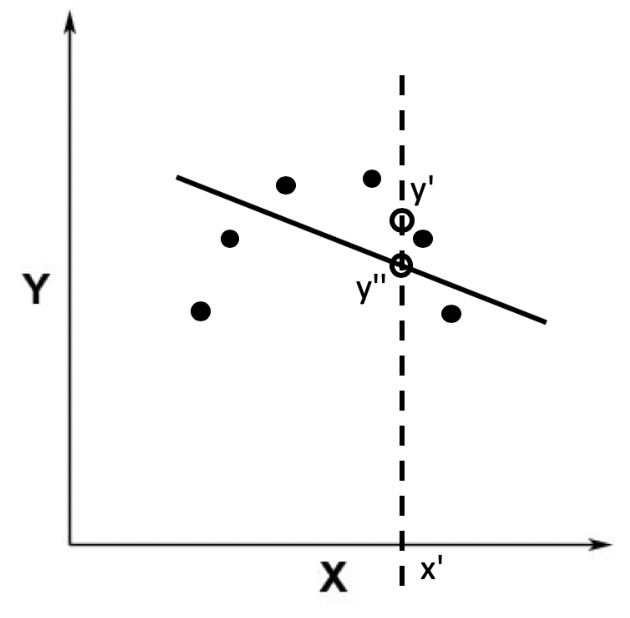
需要注意的是,使用线性回归的时候,我们都有一个前提假设,那就是数据的自变量和因变量之间呈现线性关系。如果不是线性关系,那么使用线性模型来拟合的效果一定不好。比如,之前在解释欠拟合的时候,我用过下面这个例子。
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
上面这张图的数据分布并没有表达线性关系,所以我们需要对原始的数据进行非线性的变换,或者是使用非线性的模型来拟合。
|
|||
|
|
|
|||
|
|
那么,我们如何判断一个数据集是不是能用线性模型表示呢?在线性回归中,我们可以使用决定系数R2。这个统计指标使用了回归平方和与总平方和之比,是反映模型拟合度的重要指标。它的取值在0到1之间,越接近于1表示拟合的程度越好、数据分布越接近线性关系。随着自变量个数的增加,R2将不断增大,因此我们还需要考虑方程所包含的自变量个数对R2的影响,这个时候可使用校正的决定系数Rc2。所以,在使用各种科学计算库进行线性回归时,你需要关注R2或者Rc2,来看看是不是一个好的线性拟合。在之前的代码实践中,我们提到的regression.score函数,其实就是返回了线性回归的R2。
|
|||
|
|
|
|||
|
|
## 总结
|
|||
|
|
|
|||
|
|
今天我们使用了具体的案例来推导最小二乘法的计算过程,并用Python代码进行了验证。通过最近3节的讲解,相信你对线性方程组求精确解、求近似解、以及如何在线性回归中运用这些方法,有了更加深入的理解。
|
|||
|
|
|
|||
|
|
实际上,从广义上来说,最小二乘法不仅可以用于线性回归,还可以用于非线性的回归。其主要思想还是要确保误差ε最小,但是由于现在的函数是非线性的,所以不能使用求多元方程求解的办法来得到参数估计值,而需要采用迭代的优化算法来求解,比如梯度下降法、随机梯度下降法和牛顿法。
|
|||
|
|
|
|||
|
|
## 思考题
|
|||
|
|
|
|||
|
|
我这里给出一个新的方程组,请通过最小二乘法推算出系数的近似解,并使用你熟悉的语言进行验证。
|
|||
|
|
|
|||
|
|
$b\_1+b\_2·3+b\_3·(-7)=-7.5$
|
|||
|
|
$b\_1·2+b\_2·5+b\_3·4=5.2$
|
|||
|
|
$b\_1·(-3)+b\_2·(-7)+b\_3·(-2)=-7.5$
|
|||
|
|
$b\_1·1+b\_2·4+b\_3·(-12)=-15$
|
|||
|
|
|
|||
|
|
欢迎留言和我分享,也欢迎你在留言区写下今天的学习笔记。你可以点击“请朋友读”,把今天的内容分享给你的好友,和他一起精进。
|
|||
|
|
|