151 lines
11 KiB
Markdown
151 lines
11 KiB
Markdown
|
|
# 37 | 矩阵(上):如何使用矩阵操作进行PageRank计算?
|
|||
|
|
|
|||
|
|
你好,我是黄申。今天我来说说矩阵。
|
|||
|
|
|
|||
|
|
前面我说过,矩阵由多个长度相等的向量组成,其中的每列或者每行就是一个向量。从数据结构的角度来看,我们可以把向量看作一维数组,把矩阵看作二维数组。
|
|||
|
|
|
|||
|
|
具有了二维数组的特性,矩阵就可以表达二元关系了,例如图中结点的邻接关系,或者是用户对物品的评分关系。而通过矩阵上的各种运算操作,我们就可以挖掘这些二元关系,在不同的应用场景下达到不同的目的。今天我就从图的邻接矩阵出发,展示如何使用矩阵计算来实现PageRank算法。
|
|||
|
|
|
|||
|
|
## 回顾PageRank链接分析算法
|
|||
|
|
|
|||
|
|
在讲马尔科夫模型的时候,我已经介绍了PageRank链接分析算法。所以,在展示这个算法和矩阵操作的关系之前,我们快速回顾一下它的核心思想。
|
|||
|
|
|
|||
|
|
PageRank是基于马尔科夫链的。它假设了一个“随机冲浪者”模型,冲浪者从某张网页出发,根据Web图中的链接关系随机访问。在每个步骤中,冲浪者都会从当前网页的链出网页中,随机选取一张作为下一步访问的目标。此外,PageRank还引入了随机的跳转操作,这意味着冲浪者不是按Web图的拓扑结构走下去,只是随机挑选了一张网页进行跳转。
|
|||
|
|
|
|||
|
|
基于之前的假设,PageRank的公式定义如下:
|
|||
|
|
|
|||
|
|
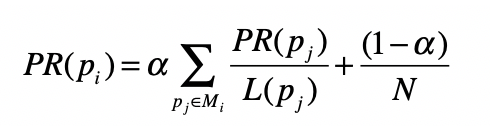
|
|||
|
|
|
|||
|
|
其中,$p\_{i}$表示第$i$张网页,$M\_{i}$是$p\_{i}$的入链接集合,$p\_{j}$是$M\_{i}$集合中的第$j$张网页。$PR\_{(p\_{j})}$表示网页$p\_{j}$的PageRank得分,$L\_{(p\_{j})}$表示网页$p\_{j}$的出链接数量,$\\frac{1}{L\_{(p\_{j})}}$就表示从网页$p\_{j}$跳转到$p\_{i}$的概率。$α$是用户不进行随机跳转的概率,$N$表示所有网页的数量。
|
|||
|
|
|
|||
|
|
PageRank的计算是采用迭代法实现的:一开始所有网页结点的初始PageRank值都可以设置为某个相同的数,例如1,然后我们通过上面这个公式,得到每个结点新的PageRank值。每当一张网页的PageRank发生了改变,它也会影响它的出链接所指向的网页,因此我们可以再次使用这个公式,循环地修正每个网页结点的值。由于这是一个马尔科夫过程,所以我们能从理论上证明,所有网页的PageRank最终会达到一个稳定的数值。整个证明过程很复杂,这里我们只需要知道这个迭代计算的过程就行了。
|
|||
|
|
|
|||
|
|
## 简化PageRank公式
|
|||
|
|
|
|||
|
|
那么,这个计算公式和矩阵操作又有什么联系呢?为了把问题简化,我们暂时不考虑随机跳转的情况,而只考虑用户按照网页间链接进行随机冲浪。那么PageRank的公式就简化为:
|
|||
|
|
|
|||
|
|

|
|||
|
|
|
|||
|
|
这个公式只包含了原公式中的$Σ\\frac{PR\_{(p\_{j})}}{L\_{(p\_{j})})}$部分。我们再来对比看看矩阵点乘的计算公式。
|
|||
|
|
|
|||
|
|

|
|||
|
|
|
|||
|
|
以上两个公式在形式上是基本一致的。因此,我们可以把$Σ\\frac{PR\_{(p\_{j})}}{L\_{(p\_{j})})}$的计算,分解为两个矩阵的点乘。一个矩阵是当前每张网页的PageRank得分,另一个矩阵就是邻接矩阵。所谓邻接矩阵,其实就是表示图结点相邻关系的矩阵。
|
|||
|
|
|
|||
|
|
假设$x\_{i,j}$是矩阵中第$i$行、第$j$列的元素,那么我们就可以使用$x\_{i,j}$表示从结点$i$到结点$j$的连接,放到PageRank的应用场景,$x\_{i,j}$就表示网页$p\_{i}$到网页$p\_{j}$的链接。最原始的邻接矩阵所包含的元素是0或1,0表示没有链接,而1表示有链接。
|
|||
|
|
|
|||
|
|
考虑到PageRank里乘积是$\\frac{1}{L\_{(p\_{j})}}$,我们可以对邻接矩阵的每一行进行归一化,用原始的值(0或1)除以$L\_{(p\_{j})}$,而$L\_{(p\_{j})}$表示有某张网页$p\_{j}$的出链接,正好是矩阵中$p\_{j}$这一行的和。所以,我们可以对原始的邻接矩阵,进行基于行的归一化,这样就能得到每个元素为$\\frac{1}{L\_{(p\_{j})}}$的矩阵,其中$j$表示矩阵的第$j$行。注意,这里的归一化是指让所有元素加起来的和为1。
|
|||
|
|
|
|||
|
|
为了方便你理解,我用下面这个拓扑图作为例子给你详细解释。
|
|||
|
|
|
|||
|
|

|
|||
|
|
|
|||
|
|
基于上面这个图,原始矩阵为:
|
|||
|
|
|
|||
|
|

|
|||
|
|
|
|||
|
|
其中第i行、第j列的元素值表示从结点i到j是不是存在链接。如果是,那么这个值为1;否则就为0。
|
|||
|
|
|
|||
|
|
按照每一行的和,分别对每一行进行归一化之后的矩阵就变为:
|
|||
|
|
|
|||
|
|

|
|||
|
|
|
|||
|
|
有了上述这个邻接矩阵,我们就可以开始最简单的PageRank计算。PageRank的计算是采用迭代法实现的。这里我把初始值都设为1,并把第一次计算的结果列在这里。
|
|||
|
|
|
|||
|
|

|
|||
|
|
|
|||
|
|
好了,我们已经成功迈出了第一步,但是还需要考虑随机跳转的可能性。
|
|||
|
|
|
|||
|
|
## 考虑随机跳转
|
|||
|
|
|
|||
|
|
经过上面的步骤,我们已经求得$Σ\\frac{PR\_{(p\_{j})}}{L\_{(p\_{j})})}$部分。不过,PageRank引入了随机跳转的机制。这一部分其实也是可以通过矩阵的点乘来实现的。我们把$Σ\\frac{PR\_{(p\_{j})}}{L\_{(p\_{j})})}$部分用$A$表示,那么完整的PageRank公式就可以表示为:
|
|||
|
|
|
|||
|
|
$PR\_{(P\_{i})}=αA+\\frac{1-α}{N}$
|
|||
|
|
|
|||
|
|
于是,我们可以把上述公式分解为如下两个矩阵的点乘:
|
|||
|
|
|
|||
|
|

|
|||
|
|
|
|||
|
|
我们仍然使用前面的例子,来看看经过随机跳转之后,PageRank值变成了多少。这里$α$取0.9。
|
|||
|
|
|
|||
|
|

|
|||
|
|
|
|||
|
|
我们前面提到,PageRank算法需要迭代式计算。为了避免计算后的数值越来越大甚至溢出,我们可以进行归一化处理,保证所有结点的数值之和为1。经过这个处理之后,我们得到第一轮的PageRank数值,也就是下面这个行向量:
|
|||
|
|
|
|||
|
|
\[0.37027027 0.24864865 0.37027027 0.00540541 0.00540541\]
|
|||
|
|
|
|||
|
|
接下来,我们只需要再重复之前的步骤,直到每个结点的值趋于稳定就可以了。
|
|||
|
|
|
|||
|
|
## 使用Python进行实现
|
|||
|
|
|
|||
|
|
说到这里,我已经把如何把整个PageRank的计算,转换成多个矩阵的点乘这个过程讲完了。这样一来,我们就可以利用Python等科学计算语言提供的库,来完成基于PageRank的链接分析。为了展示具体的代码,我以之前的拓扑图为例,给你详细讲述每一步。
|
|||
|
|
|
|||
|
|
首先,我们要进行一些初始化工作,包括设置结点数量、确定随机跳转概率的$α$、代表拓扑图的邻接矩阵以及存放所有结点PageRank值的数组。下面是一段示例代码,在代码中我提供了注释供你参考。
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
import numpy as np
|
|||
|
|
|
|||
|
|
# 设置确定随机跳转概率的alpha、网页结点数
|
|||
|
|
alpha = 0.9
|
|||
|
|
N = 5
|
|||
|
|
|
|||
|
|
# 初始化随机跳转概率的矩阵
|
|||
|
|
jump = np.full([2,1], [[alpha], [1-alpha]], dtype=float)
|
|||
|
|
|
|||
|
|
# 邻接矩阵的构建
|
|||
|
|
adj = np.full([N,N], [[0,0,1,0,0],[1,0,1,0,0],[1,0,0,0,0],[0,0,0,0,0],[0,1,0,0,0]], dtype=float)
|
|||
|
|
|
|||
|
|
# 对邻接矩阵进行归一化
|
|||
|
|
row_sums = adj.sum(axis=1) # 对每一行求和
|
|||
|
|
row_sums[row_sums == 0] = 0.1 # 防止由于分母出现0而导致的Nan
|
|||
|
|
adj = adj / row_sums[:, np.newaxis] # 除以每行之和的归一化
|
|||
|
|
|
|||
|
|
# 初始的PageRank值,通常是设置所有值为1.0
|
|||
|
|
pr = np.full([1,N], 1, dtype=float)
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
之后,我们就能采用迭代法来计算PageRank值。一般我们通过比较每个结点最近两次计算的值是否足够接近,来确定数值是不是已经稳定,以及是不是需要结束迭代。这里为简便起见,我使用了固定次数的循环来实现。如果你的拓扑图比较复杂,需要更多次迭代,我把示例代码和注释列在这里。
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
# PageRank算法本身是采用迭代方式进行的,当最终的取值趋于稳定后结束。
|
|||
|
|
for i in range(0, 20):
|
|||
|
|
|
|||
|
|
# 进行点乘,计算Σ(PR(pj)/L(pj))
|
|||
|
|
pr = np.dot(pr, adj)
|
|||
|
|
|
|||
|
|
# 转置保存Σ(PR(pj)/L(pj))结果的矩阵,并增加长度为N的列向量,其中每个元素的值为1/N,便于下一步的点乘。
|
|||
|
|
pr_jump = np.full([N, 2], [[0, 1/N]])
|
|||
|
|
pr_jump[:,:-1] = pr.transpose()
|
|||
|
|
|
|||
|
|
# 进行点乘,计算α(Σ(PR(pj)/L(pj))) + (1-α)/N)
|
|||
|
|
pr = np.dot(pr_jump, jump)
|
|||
|
|
|
|||
|
|
# 归一化PageRank得分
|
|||
|
|
pr = pr.transpose()
|
|||
|
|
pr = pr / pr.sum()
|
|||
|
|
|
|||
|
|
print("round", i + 1, pr)
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
如果成功运行了上述两段代码,你就能看到每个结点最终获得的PageRank分数是多少。
|
|||
|
|
|
|||
|
|
Python中还有一些很不错的库,提供了直接构建拓扑图和计算PageRank的功能,例如networkx([https://networkx.github.io/](https://networkx.github.io/))。你可以尝试使用这种库,构建样例拓扑图并计算每个结点的PageRank得分,最后和上述代码所计算的PageRank得分进行比较,验证一下上述代码的结果是不是合理。
|
|||
|
|
|
|||
|
|
## 总结
|
|||
|
|
|
|||
|
|
我们可以把向量看作一维数组,把矩阵看作二维数组。矩阵的点乘,是由若干个向量的点乘组成的,所以我们可以通过矩阵的点乘操作,挖掘多组向量两两之间的关系。
|
|||
|
|
|
|||
|
|
今天我们讲了矩阵的点乘操作在PageRank算法中的应用。通过表示网页的邻接二元关系,我们可以使用矩阵来计算PageRank的得分。在这个应用场景下,矩阵点乘体现了多个马尔科夫过程中的状态转移。
|
|||
|
|
|
|||
|
|
矩阵点乘和其他运算操作,还可以运用在很多其他的领域。例如,我在上一节介绍K均值聚类算法时,就提到了需要计算某个数据点向量、其他数据点向量之间的距离或者相似度,以及使用多个数据点向量的平均值来获得质心点的向量,这些都可以通过矩阵操作来完成。
|
|||
|
|
|
|||
|
|
另外,在协同过滤的推荐中,我们可以使用矩阵点乘,来实现多个用户或者物品之间的相似程度,以及聚集后的相似程度所导致的最终推荐结果。下一节,我会使用矩阵来表示用户和物品的二元关系,并通过矩阵来计算协同过滤的结果。
|
|||
|
|
|
|||
|
|
## 思考题
|
|||
|
|
|
|||
|
|
在介绍PageRank算法时,我提到了它的计算是一个迭代的过程。这一节我使用了固定次数的循环来实现这一点。请尝试使用计算前后两次PageRank数值的差,来判断是否需要结束迭代。(提示:你可以使用矩阵元素对应的减法,以及在第3讲和加餐2中提到的相对误差。)
|
|||
|
|
|
|||
|
|
欢迎留言和我分享,也欢迎你在留言区写下今天的学习笔记。你可以点击“请朋友读”,把今天的内容分享给你的好友,和他一起精进。
|
|||
|
|
|