|
|
|
|
|
# 33 | 线性代数:线性代数到底都讲了些什么?
|
|
|
|
|
|
|
|
|
|
|
|
你好,我是黄申。
|
|
|
|
|
|
|
|
|
|
|
|
通过第二模块的学习,我想你对概率统计在编程领域,特别是机器学习算法中的应用,已经有了一定理解。概率统计关注的是随机变量及其概率分布,以及如何通过观测数据来推断这些分布。可是,在解决很多问题的时候,我们不仅要关心单个变量之间的关系,还要进一步研究多个变量之间的关系,最典型的例子就是基于多个特征的信息检索和机器学习。
|
|
|
|
|
|
|
|
|
|
|
|
在信息检索中,我们需要考虑多个关键词特征对最终相关性的影响,而在机器学习中,无论是监督式还是非监督式学习,我们都需要考虑多个特征对模型拟合的影响。在研究多个变量之间关系的时候,线性代数成为了解决这类问题的有力工具。
|
|
|
|
|
|
|
|
|
|
|
|
另一方面,在我们日常生活和工作中,很多问题都可以线性化,小到计算两个地点之间的距离,大到计算互联网中全部网页的PageRank。所以,为了使用编程来解决相应的问题,我们也必须掌握一些必要的线性代数基础知识。因此,我会从线性代数的基本概念出发,结合信息检索和机器学习领域的知识,详细讲解线性代数的运用。
|
|
|
|
|
|
|
|
|
|
|
|
关于线性代数,究竟都需要掌握哪些方面的知识呢?我们今天就来看一看,让你对之后一段时间所要学习的知识有个大体的了解。
|
|
|
|
|
|
|
|
|
|
|
|
## 向量和向量空间
|
|
|
|
|
|
|
|
|
|
|
|
我们之前所谈到的变量都属于**标量**(Scalar)。它只是一个单独的数字,而且不能表示方向。从计算机数据结构的角度来看,标量就是编程中最基本的变量。这个很好理解,你可以回想一下刚开始学习编程时接触到的标量类型的变量。
|
|
|
|
|
|
|
|
|
|
|
|
和标量对应的概念,就是线性代数中最常用、也最重要的概念,**向量**(Vector),也可以叫做矢量。它代表一组数字,并且这些数字是有序排列的。我们用数据结构的视角来看,向量可以用数组或者链表来表达。
|
|
|
|
|
|
|
|
|
|
|
|
后面的文章里,我会用加粗的小写字母表示一个向量,例如$x$,而$x\_{1},x\_{2},x\_{3},…,x\_{n}$等等,来表示向量中的每个元素,这里面的n就是向量的维。
|
|
|
|
|
|
|
|
|
|
|
|
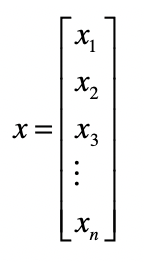
|
|
|
|
|
|
|
|
|
|
|
|
向量和标量最大的区别在于,向量除了拥有数值的大小,还拥有方向。向量或者矢量中的“向”和“矢”这两个字,都表明它们是有方向的。你可能会问,为什么这一串数字能表示方向呢?
|
|
|
|
|
|
|
|
|
|
|
|
这是因为,如果我们把某个向量中的元素看作坐标轴上的坐标,那么这个向量就可以看作空间中的一个点。以原点为起点,以向量代表的点为终点,就能形成一条有向直线。而这样的处理其实已经给向量赋予了代数的含义,使得计算的过程中更加直观。在后面讨论向量空间、向量夹角、矩阵特征值等概念的时候,我会进一步展示给你看。
|
|
|
|
|
|
|
|
|
|
|
|
由于一个向量包含了很多个元素,因此我们自然地就可以把它运用在机器学习的领域。上一个模块,我讲过如何把自然界里物体的属性,转换为能够用数字表达的特征。由于特征有很多维,因此我们可以使用向量来表示某个物体的特征。其中,向量的每个元素就代表一维特征,而元素的值代表了相应特征的值,我们称这类向量为**特征向量**(Feature Vector)。
|
|
|
|
|
|
|
|
|
|
|
|
需要注意的是,这个特征向量和**矩阵的特征向量**(Eigenvector)是两码事。那么矩阵的特征向量是什么意思呢?矩阵的几何意义是坐标的变换。如果一个矩阵存在特征向量和特征值,那么这个矩阵的特征向量就表示了它在空间中最主要的运动方向。如果你对这几个概念还不太理解,也不用担心,在介绍矩阵的时候,我会详细说说什么是矩阵的特征向量。
|
|
|
|
|
|
|
|
|
|
|
|
## 向量的运算
|
|
|
|
|
|
|
|
|
|
|
|
标量和向量之间可以进行运算,比如标量和向量相加或者相乘时,我们直接把标量和向量中的每个元素相加或者相乘就行了,这个很好理解。可是,向量和向量之间的加法或乘法应该如何进行呢?我们需要先定义向量空间。向量空间理论上的定义比较繁琐,不过二维或者三维的坐标空间可以很好地帮助你来理解。这些空间主要有几个特性:
|
|
|
|
|
|
|
|
|
|
|
|
* 空间由无穷多个的位置点组成;
|
|
|
|
|
|
|
|
|
|
|
|
* 这些点之间存在相对的关系;
|
|
|
|
|
|
|
|
|
|
|
|
* 可以在空间中定义任意两点之间的长度,以及任意两个向量之间的角度;
|
|
|
|
|
|
|
|
|
|
|
|
* 这个空间的点可以进行移动。
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
有了这些特点,我们就可以定义向量之间的加法、乘法(或点乘)、距离和夹角等等。
|
|
|
|
|
|
|
|
|
|
|
|
两个向量之间的加法,首先它们需要维度相同,然后是对应的元素相加。
|
|
|
|
|
|
|
|
|
|
|
|
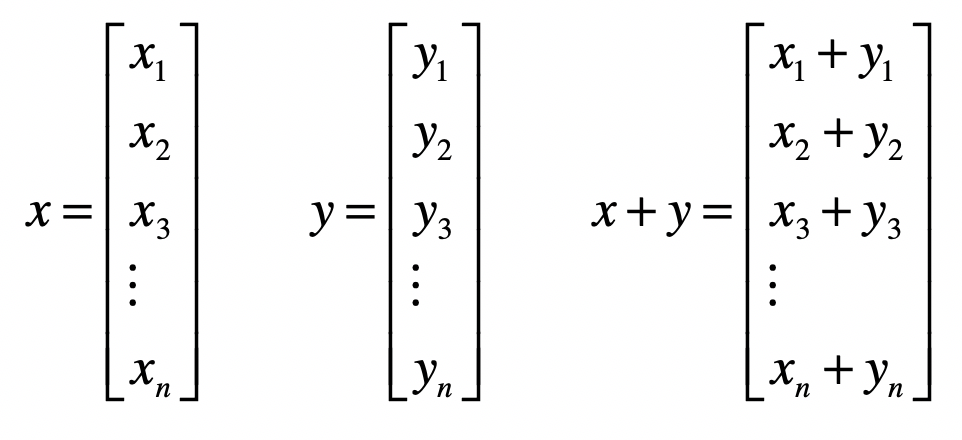
|
|
|
|
|
|
|
|
|
|
|
|
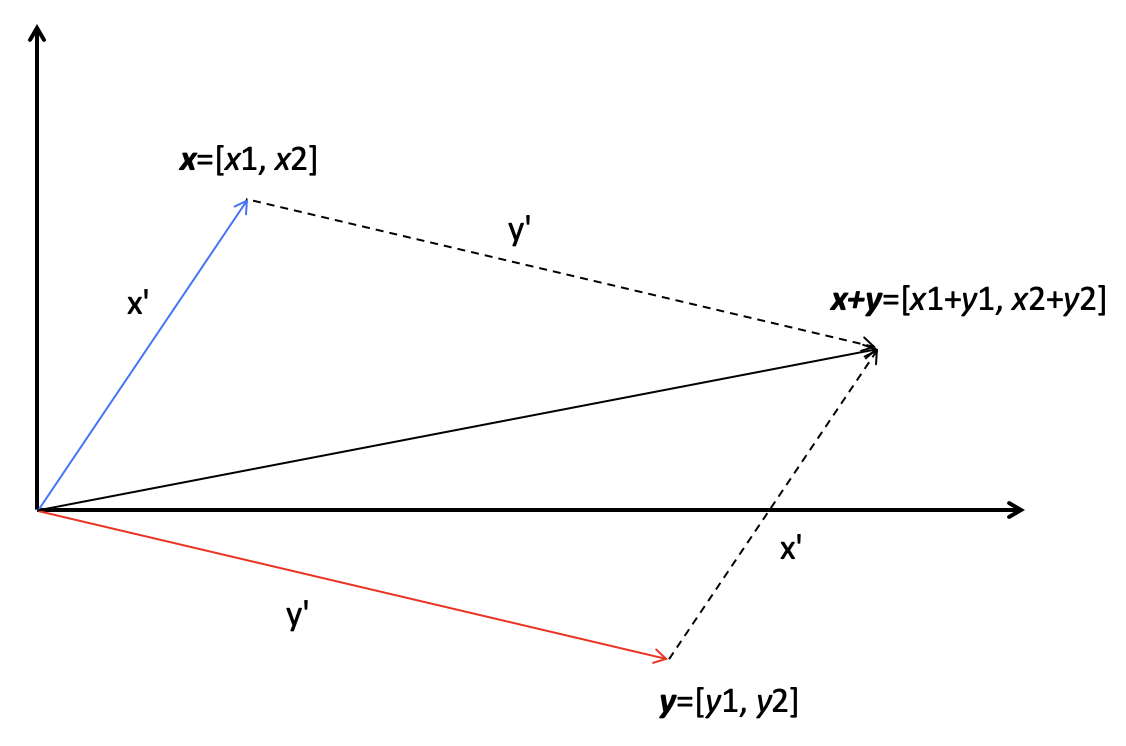
所以说,向量的加法实际上就是把几何问题转化成了代数问题,然后用代数的方法实现了几何的运算。我下面画了一张图,来解释二维空间里,两个向量的相加,看完你就能理解了。
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
在这张图中,有两个向量x和y,它们的长度分别是x’和y’,它们的相加结果是x+y,这个结果所对应的点相当于x向量沿着y向量的方向移动y’,或者是y向量沿着x向量的方向移动x’。
|
|
|
|
|
|
|
|
|
|
|
|
向量之间的乘法默认是点乘,向量x和y的点乘是这么定义的:
|
|
|
|
|
|
|
|
|
|
|
|

|
|
|
|
|
|
|
|
|
|
|
|
点乘的作用是把相乘的两个向量转换成了标量,它有具体的几何含义。我们会用点乘来计算向量的长度以及两个向量间的夹角,所以一般情况下我们会默认向量间的乘法是点乘。至于向量之间的夹角和距离,它们在向量空间模型(Vector Space Model)中发挥了重要的作用。信息检索和机器学习等领域充分利用了向量空间模型,计算不同对象之间的相似程度。在之后的专栏里,我会通过向量空间模型,详细介绍向量点乘,以及向量间夹角和距离的计算。
|
|
|
|
|
|
|
|
|
|
|
|
## 矩阵的运算
|
|
|
|
|
|
|
|
|
|
|
|
矩阵由多个长度相等的向量组成,其中的每列或者每行就是一个向量。因此,我们把向量延伸一下就能得到矩阵(Matrix)。
|
|
|
|
|
|
|
|
|
|
|
|
从数据结构的角度看,向量是一维数组,那矩阵就是一个二维数组。如果二维数组里绝大多数元素都是0或者不存在的值,那么我们就称这个矩阵很稀疏(Sparse)。对于稀疏矩阵,我们可以使用哈希表的链地址法来表示。所以,矩阵中的每个元素有两个索引。
|
|
|
|
|
|
|
|
|
|
|
|
我用加粗的斜体大写字母表示一个矩阵,例如$X$,而$X\_{12},X\_{22},…,X\_{nm}$等等,表示矩阵中的每个元素,而这里面的n和m分别表示矩阵的行维数和列维数。
|
|
|
|
|
|
|
|
|
|
|
|
我们换个角度来看,向量其实也是一种特殊的矩阵。如果一个矩阵是n × m维,那么一个n × 1的矩阵也可以称作一个n维列向量;而一个1 × m矩阵也称为一个m维行向量。
|
|
|
|
|
|
|
|
|
|
|
|
同样,我们也可以定义标量和矩阵之间的加法和乘法,我们只需要把标量和矩阵中的每个元素相加或相乘就可以了。剩下的问题就是,矩阵和矩阵之间是如何进行加法和乘法的呢?矩阵加法比较简单,只要保证参与操作的两个矩阵具有相同的行维度和列维度,我们就可以把对应的元素两两相加。而乘法略微繁琐一些,如果写成公式就是这种形式:
|
|
|
|
|
|
|
|
|
|
|
|

|
|
|
|
|
|
|
|
|
|
|
|
其中,矩阵$Z$为矩阵$X$和$Y$的乘积,$X$是形状为i x k的矩阵,而$Y$是形状为k × j的矩阵。$X$的列数k必须和$Y$的行数k相等,两者才可以进行这样的乘法。
|
|
|
|
|
|
|
|
|
|
|
|
我们可以把这个过程看作矩阵$X$的行向量和矩阵$Y$的列向量两两进行点乘,我这里画了张图,你理解了这张图就不难记住这个公式了。
|
|
|
|
|
|
|
|
|
|
|
|

|
|
|
|
|
|
|
|
|
|
|
|
两个矩阵中对应元素进行相乘,这种操作也是存在的,我们称它为元素**对应乘积**,或者Hadamard乘积。但是这种乘法咱们用得比较少,所以你只要知道有这个概念就可以了。
|
|
|
|
|
|
|
|
|
|
|
|
除了加法和乘法,矩阵还有一些其他重要的操作,包括转置、求逆矩阵、求特征值和求奇异值等等。
|
|
|
|
|
|
|
|
|
|
|
|
**转置**(Transposition)是指矩阵内的元素行索引和纵索引互换,例如$X\_{ij}$就变为$X\_{ji}$,相应的,矩阵的形状由转置前的n × m变为转置后的m × n。从几何的角度来说,矩阵的转置就是原矩阵以对角线为轴进行翻转后的结果。下面这张图展示了矩阵$X$转置之后的矩阵$X’$:
|
|
|
|
|
|
|
|
|
|
|
|

|
|
|
|
|
|
|
|
|
|
|
|
除了转置矩阵,另一个重要的概念是逆矩阵。为了理解逆矩阵或矩阵逆(Matrix Inversion),我们首先要理解单位矩阵(Identity Matrix)。单位矩阵中,所有沿主对角线的元素都是1,而其他位置的所有元素都是0。通常我们只考虑单位矩阵为方阵的情况,也就是行数和列数相等,我们把它记作$I\_{n}$,$n$表示维数。我这里给出一个$I\_{5}$的示例。
|
|
|
|
|
|
|
|
|
|
|
|
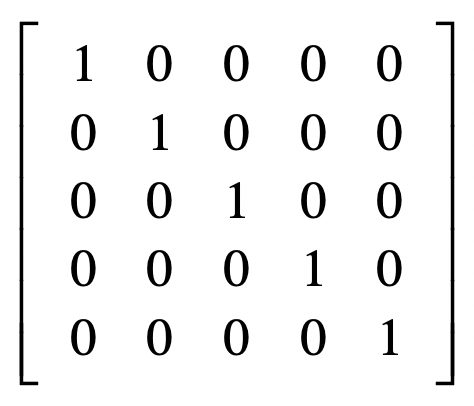
|
|
|
|
|
|
|
|
|
|
|
|
如果有矩阵$X$,我们把它的逆矩阵记做$X^{-1}$,两者相乘的结果是单位矩阵,写成公式就是这种形式:
|
|
|
|
|
|
|
|
|
|
|
|

|
|
|
|
|
|
|
|
|
|
|
|
特征值和奇异值的概念以及求解比较复杂,从大体上来理解,它们可以帮助我们找到矩阵最主要的特点。通过这些操作,我们就可以在机器学习算法中降低特征向量的维度,达到特征选择和变换的目的。我会在后面的专栏,结合案例给你详细讲解。
|
|
|
|
|
|
|
|
|
|
|
|
## 总结
|
|
|
|
|
|
|
|
|
|
|
|
相对于概率统计,线性代数中的基本概念和知识点可能没有那么多。但是对于刚入门的初学者,这些内容理解起来会比较费力。在这一节里,我进行了大致的梳理,帮助你学习。
|
|
|
|
|
|
|
|
|
|
|
|
标量和向量的区别,标量只是单独的一个数,而向量是一组数。矩阵是向量的扩展,就是一个二维数组。我们可以使用哈希表的链地址法表示稀疏矩阵。
|
|
|
|
|
|
|
|
|
|
|
|
标量和向量或矩阵的加法、乘法比较简单,就是把这个标量和向量或矩阵中所有的元素轮流进行相加或相乘。向量之间的加法和矩阵之间的加法,是把两者对应的元素相加。向量之间的相乘分为叉乘和点乘,我在专栏里默认向量乘法为点乘。而矩阵的乘法默认为左矩阵的行向量和右矩阵的列向量两两点乘。
|
|
|
|
|
|
|
|
|
|
|
|
说到这里,你可能还是不太理解线性代数对于编程有什么用处。在这个模块之后的内容中,我会详细介绍向量空间模型、线性方程组、矩阵求特征值和奇异值分解等,在信息检索和机器学习领域中,有怎样的应用场景。
|
|
|
|
|
|
|
|
|
|
|
|
## 思考题
|
|
|
|
|
|
|
|
|
|
|
|
之前你对线性代数的认识是什么样的呢?对这块内容,你觉得最难的是什么?
|
|
|
|
|
|
|
|
|
|
|
|
欢迎留言和我分享,也欢迎你在留言区写下今天的学习笔记。你可以点击“请朋友读”,把今天的内容分享给你的好友,和他一起精进。
|
|
|
|
|
|
|