102 lines
9.5 KiB
Markdown
102 lines
9.5 KiB
Markdown
|
|
# 15 | 浮点数和定点数(上):怎么用有限的Bit表示尽可能多的信息?
|
|||
|
|
|
|||
|
|
在我们日常的程序开发中,不只会用到整数。更多情况下,我们用到的都是实数。比如,我们开发一个电商App,商品的价格常常会是9块9;再比如,现在流行的深度学习算法,对应的机器学习里的模型里的各个权重也都是1.23这样的数。可以说,在实际的应用过程中,这些有零有整的实数,是和整数同样常用的数据类型,我们也需要考虑到。
|
|||
|
|
|
|||
|
|
## 浮点数的不精确性
|
|||
|
|
|
|||
|
|
那么,我们能不能用二进制表示所有的实数,然后在二进制下计算它的加减乘除呢?先不着急,我们从一个有意思的小案例来看。
|
|||
|
|
|
|||
|
|
你可以在Linux下打开Python的命令行Console,也可以在Chrome浏览器里面通过开发者工具,打开浏览器里的Console,在里面输入“0.3 + 0.6”,然后看看你会得到一个什么样的结果。
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
>>> 0.3 + 0.6
|
|||
|
|
0.8999999999999999
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
不知道你有没有大吃一惊,这么简单的一个加法,无论是在Python还是在JavaScript里面,算出来的结果居然不是准确的0.9,而是0.8999999999999999这么个结果。这是为什么呢?
|
|||
|
|
|
|||
|
|
在回答为什么之前,我们先来想一个更抽象的问题。通过前面的这么多讲,你应该知道我们现在用的计算机通常用16/32个比特(bit)来表示一个数。那我问你,我们用32个比特,能够表示所有实数吗?
|
|||
|
|
|
|||
|
|
答案很显然是不能。32个比特,只能表示2的32次方个不同的数,差不多是40亿个。如果表示的数要超过这个数,就会有两个不同的数的二进制表示是一样的。那计算机可就会一筹莫展,不知道这个数到底是多少。
|
|||
|
|
|
|||
|
|
40亿个数看似已经很多了,但是比起无限多的实数集合却只是沧海一粟。所以,这个时候,计算机的设计者们,就要面临一个问题了:我到底应该让这40亿个数映射到实数集合上的哪些数,在实际应用中才能最划得来呢?
|
|||
|
|
|
|||
|
|
## 定点数的表示
|
|||
|
|
|
|||
|
|
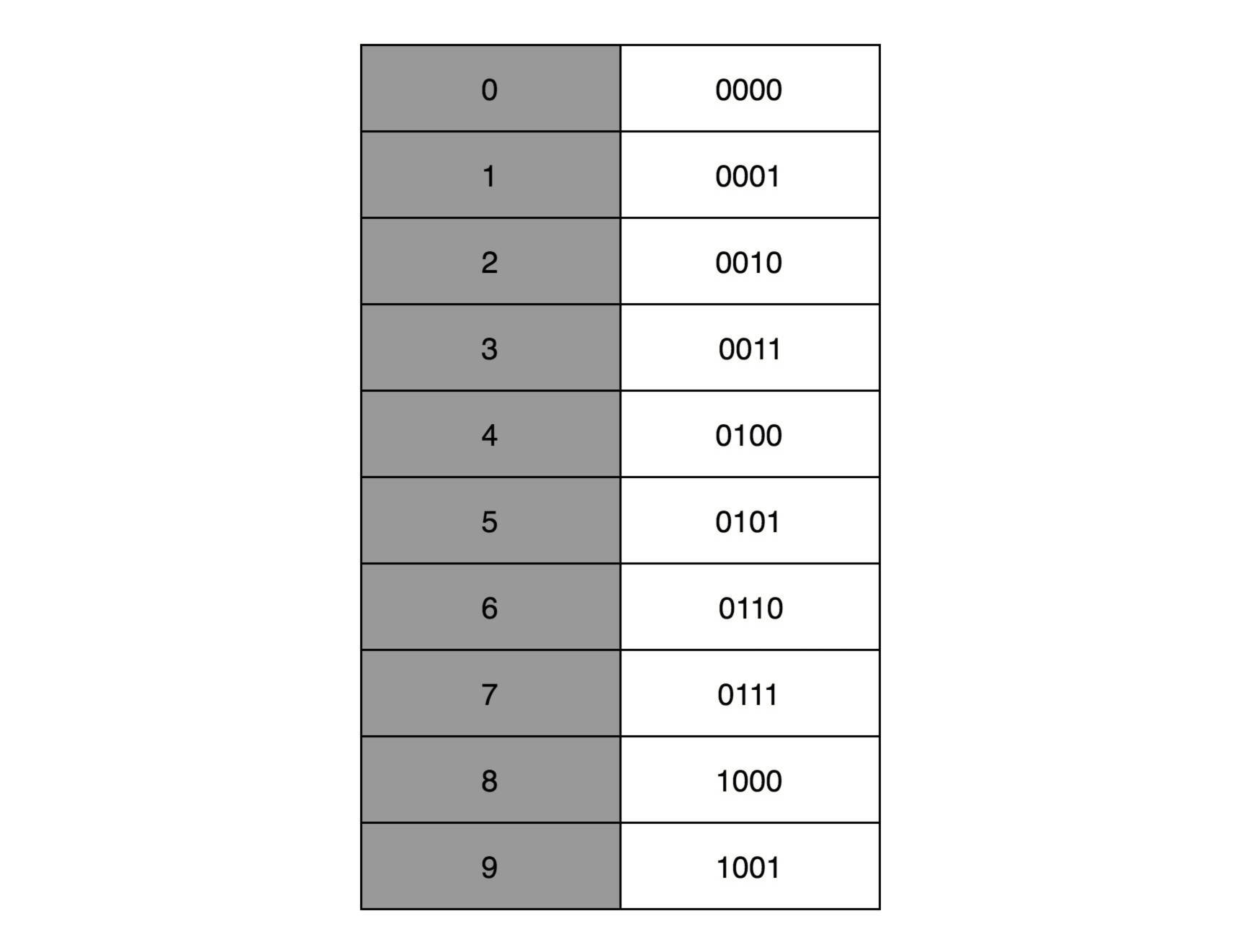
有一个很直观的想法,就是我们用4个比特来表示0~9的整数,那么32个比特就可以表示8个这样的整数。然后我们把最右边的2个0~9的整数,当成小数部分;把左边6个0~9的整数,当成整数部分。这样,我们就可以用32个比特,来表示从0到999999.99这样1亿个实数了。
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
这种用二进制来表示十进制的编码方式,叫作[**BCD编码**](https://zh.wikipedia.org/wiki/%E4%BA%8C%E9%80%B2%E7%A2%BC%E5%8D%81%E9%80%B2%E6%95%B8)(Binary-Coded Decimal)。其实它的运用非常广泛,最常用的是在超市、银行这样需要用小数记录金额的情况里。在超市里面,我们的小数最多也就到分。这样的表示方式,比较直观清楚,也满足了小数部分的计算。
|
|||
|
|
|
|||
|
|
不过,这样的表示方式也有几个缺点。
|
|||
|
|
|
|||
|
|
**第一,这样的表示方式有点“浪费”。**本来32个比特我们可以表示40亿个不同的数,但是在BCD编码下,只能表示1亿个数,如果我们要精确到分的话,那么能够表示的最大金额也就是到100万。如果我们的货币单位是人民币或者美元还好,如果我们的货币单位变成了津巴布韦币,这个数量就不太够用了。
|
|||
|
|
|
|||
|
|
**第二,这样的表示方式没办法同时表示很大的数字和很小的数字。**我们在写程序的时候,实数的用途可能是多种多样的。有时候我们想要表示商品的金额,关心的是9.99这样小的数字;有时候,我们又要进行物理学的运算,需要表示光速,也就是$3×10^8$这样很大的数字。那么,我们有没有一个办法,既能够表示很小的数,又能表示很大的数呢?
|
|||
|
|
|
|||
|
|
## 浮点数的表示
|
|||
|
|
|
|||
|
|
答案当然是有的,就是你可能经常听说过的**浮点数**(Floating Point),也就是**float类型**。
|
|||
|
|
|
|||
|
|
我们先来想一想。如果我们想在一张便签纸上,用一行来写一个十进制数,能够写下多大范围的数?因为我们要让人能够看清楚,所以字最小也有一个限制。你会发现一个和上面我们用BCD编码表示数一样的问题,就是纸张的宽度限制了我们能够表示的数的大小。如果宽度只放得下8个数字,那么我们还是只能写下最大到99999999这样的数字。
|
|||
|
|
|
|||
|
|

|
|||
|
|
|
|||
|
|
有限宽度的便签,只能写下有限大小的数字
|
|||
|
|
|
|||
|
|
其实,这里的纸张宽度,就和我们32个比特一样,是在空间层面的限制。那么,在现实生活中,我们是怎么表示一个很大的数的呢?比如说,我们想要在一本科普书里,写一下宇宙内原子的数量,莫非是用一页纸,用好多行写下很多个0么?
|
|||
|
|
|
|||
|
|
当然不是了,我们会用科学计数法来表示这个数字。宇宙内的原子的数量,大概在 10的82次方左右,我们就用$1.0×10^82$这样的形式来表示这个数值,不需要写下82个0。
|
|||
|
|
|
|||
|
|
在计算机里,我们也可以用一样的办法,用科学计数法来表示实数。浮点数的科学计数法的表示,有一个**IEEE**的标准,它定义了两个基本的格式。一个是用32比特表示单精度的浮点数,也就是我们常常说的float或者float32类型。另外一个是用64比特表示双精度的浮点数,也就是我们平时说的double或者float64类型。
|
|||
|
|
|
|||
|
|
双精度类型和单精度类型差不多,这里,我们来看单精度类型,双精度你自然也就明白了。
|
|||
|
|
|
|||
|
|

|
|||
|
|
|
|||
|
|
单精度的32个比特可以分成三部分。
|
|||
|
|
|
|||
|
|
第一部分是一个**符号位**,用来表示是正数还是负数。我们一般用**s**来表示。在浮点数里,我们不像正数分符号数还是无符号数,所有的浮点数都是有符号的。
|
|||
|
|
|
|||
|
|
接下来是一个8个比特组成的**指数位**。我们一般用**e**来表示。8个比特能够表示的整数空间,就是0~255。我们在这里用1~254映射到-126~127这254个有正有负的数上。因为我们的浮点数,不仅仅想要表示很大的数,还希望能够表示很小的数,所以指数位也会有负数。
|
|||
|
|
|
|||
|
|
你发现没,我们没有用到0和255。没错,这里的 0(也就是8个比特全部为0) 和 255 (也就是8个比特全部为1)另有它用,我们等一下再讲。
|
|||
|
|
|
|||
|
|
最后,是一个23个比特组成的**有效数位**。我们用**f**来表示。综合科学计数法,我们的浮点数就可以表示成下面这样:
|
|||
|
|
|
|||
|
|
$(-1)^s×1.f×2^e$
|
|||
|
|
|
|||
|
|
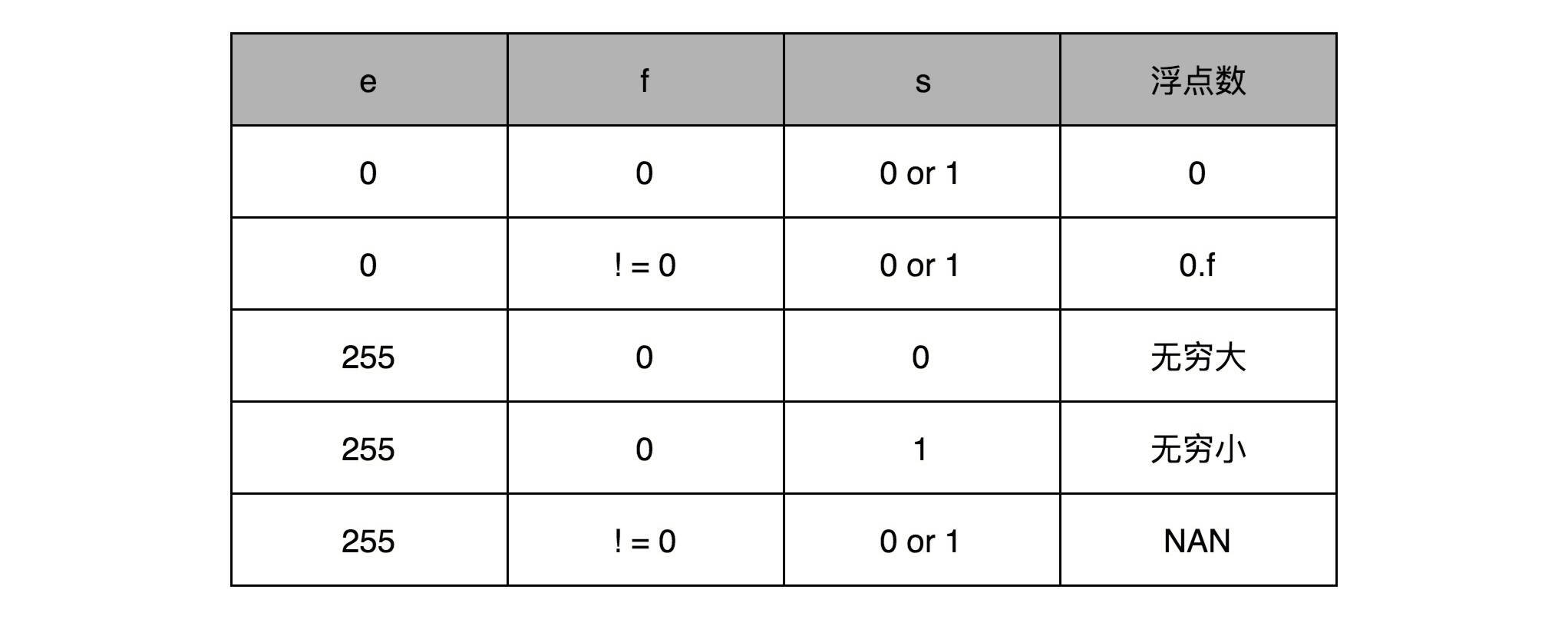
你会发现,这里的浮点数,没有办法表示0。的确,要表示0和一些特殊的数,我们就要用上在e里面留下的0和255这两个表示,这两个表示其实是两个标记位。在e为0且f为0的时候,我们就把这个浮点数认为是0。至于其它的e是0或者255的特殊情况,你可以看下面这个表格,分别可以表示出无穷大、无穷小、NAN以及一个特殊的不规范数。
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
我们可以以0.5为例子。0.5的符号为s应该是0,f应该是0,而e应该是-1,也就是
|
|||
|
|
|
|||
|
|
$0.5= (-1)^0×1.0×2^{-1}=0.5$,对应的浮点数表示,就是32个比特。
|
|||
|
|
|
|||
|
|

|
|||
|
|
|
|||
|
|
$s=0,e = 2^{-1}$,需要注意,e表示从-126到127个,-1是其中的第126个数,这里的e如果用整数表示,就是$2^6+2^5+2^4+2^3+2^2+2^1=126$,$1.f=1.0$。
|
|||
|
|
|
|||
|
|
在这样的浮点数表示下,不考虑符号的话,浮点数能够表示的最小的数和最大的数,差不多是$1.17×10^{-38}$和$3.40×10^{38}$。比前面的BCD编码能够表示的范围大多了。
|
|||
|
|
|
|||
|
|
## 总结延伸
|
|||
|
|
|
|||
|
|
你会看到,在这样的表示方式下,浮点数能够表示的数据范围一下子大了很多。正是因为这个数对应的小数点的位置是“浮动”的,它才被称为浮点数。随着指数位e的值的不同,小数点的位置也在变动。对应的,前面的BCD编码的实数,就是小数点固定在某一位的方式,我们也就把它称为**定点数**。
|
|||
|
|
|
|||
|
|
回到我们最开头,为什么我们用0.3 + 0.6不能得到0.9呢?这是因为,浮点数没有办法精确表示0.3、0.6和0.9。事实上,我们拿出0.1~0.9这9个数,其中只有0.5能够被精确地表示成二进制的浮点数,也就是s = 0、e = -1、f = 0这样的情况。
|
|||
|
|
|
|||
|
|
而0.3、0.6乃至我们希望的0.9,都只是一个近似的表达。这个也为我们带来了一个挑战,就是浮点数无论是表示还是计算其实都是近似计算。那么,在使用过程中,我们该怎么来使用浮点数,以及使用浮点数会遇到些什么问题呢?下一讲,我会用更多的实际代码案例,来带你看看浮点数计算中的各种“坑”。
|
|||
|
|
|
|||
|
|
## 推荐阅读
|
|||
|
|
|
|||
|
|
如果对浮点数的表示还不是很清楚,你可以仔细阅读一下《计算机组成与设计:硬件/软件接口》的3.5.1节。
|
|||
|
|
|
|||
|
|
## 课后思考
|
|||
|
|
|
|||
|
|
对于BCD编码的定点数,如果我们用7个比特来表示连续两位十进制数,也就是00~99,是不是可以让32比特表示更大一点的数据范围?如果我们还需要表示负数,那么一个32比特的BCD编码,可以表示的数据范围是多大?
|
|||
|
|
|
|||
|
|
欢迎你在留言区写下你的思考和疑问,和大家一起探讨。你也可以把今天的文章分享给你朋友,和他一起学习和进步。
|
|||
|
|
|