138 lines
18 KiB
Markdown
138 lines
18 KiB
Markdown
|
|
# 16 | 最近邻检索(下):如何用乘积量化实现“拍照识花”功能?
|
|||
|
|
|
|||
|
|
你好,我是陈东。
|
|||
|
|
|
|||
|
|
随着AI技术的快速发展,以图搜图、拍图识物已经是许多平台上的常见功能了。比如说,在搜索引擎中,我们可以直接上传图片进行反向搜索。在购物平台中,我们可以直接拍照进行商品搜索。包括在一些其他的应用中,我们还能拍照识别植物品种等等。这些功能都依赖于高效的图片检索技术,那它究竟是怎么实现的呢?今天,我们就来聊一聊这个问题。
|
|||
|
|
|
|||
|
|
## 聚类算法和局部敏感哈希的区别?
|
|||
|
|
|
|||
|
|
检索图片和检索文章一样,我们首先需要用向量空间模型将图片表示出来,也就是将一个图片对象转化为高维空间中的一个点。这样图片检索问题就又变成了我们熟悉的高维空间的相似检索问题。
|
|||
|
|
|
|||
|
|
如果我们把每个图片中的像素点看作一个维度,把像素点的RGB值作为该维度上的值,那一张图片的维度会是百万级别的。这么高的维度,检索起来会非常复杂,我们该怎么处理呢?我们可以像提取文章关键词一样,对图片进行特征提取来压缩维度。
|
|||
|
|
|
|||
|
|
要想实现图片特征提取,我们有很多种深度学习的方法可以选择。比如,使用卷积神经网络(CNN)提取图片特征。这样,用一个512到1024维度的向量空间模型,我们就可以很好地描述图像了,但这依然是一个非常高的维度空间。因此,我们仍然需要使用一些近似最邻近检索技术来加速检索过程。
|
|||
|
|
|
|||
|
|
一种常用的近似最邻近检索方法,是使用局部敏感哈希对高维数据进行降维处理,将高维空间的点划到有限的区域中。这样,通过判断要查询的点所在的区域,我们就能快速取出这个区域的所有候选集了。
|
|||
|
|
|
|||
|
|
不过,在上一讲中我们也提到,局部敏感哈希由于哈希函数构造相对比较简单,往往更适合计算字面上的相似性(表面特征的相似性),而不是语义上的相似性(本质上的相似性)。这怎么理解呢?举个例子,即便是面对同一种花,不同的人在不同的地点拍出来的照片,在角度、背景、花的形状上也会有比较大的差异。也就是说,这两张图片的表面特征其实差异很大,这让我们没办法利用局部敏感哈希,来合理评估它们的相似度。
|
|||
|
|
|
|||
|
|
而且,局部敏感哈希其实是一种粒度很粗的非精准检索方案。以SimHash为例,它能将上百万的高维空间压缩到64位的比特位中,这自然也会损失不少的精确性。
|
|||
|
|

|
|||
|
|
|
|||
|
|
因此,更常见的一种方案,是使用聚类算法来划分空间。和简单的局部敏感哈希算法相比,聚类算法能将空间中的点更灵活地划分成多个类,并且保留了向量的高维度,使得我们可以更准确地计算向量间的距离。好的聚类算法要保证类内的点足够接近,不同类之间的距离足够大。一种常见的聚类算法是K-means算法(K-平均算法)。
|
|||
|
|

|
|||
|
|
|
|||
|
|
K-means聚类算法的思想其实很“朴素”,它将所有的点划分为k个类,每个类都有一个**类中心向量**。在构建聚类的时候,我们希望每个类内的点都是紧密靠近类中心的。用严谨的数学语言来说,K-means聚类算法的优化目标是,**类内的点到类中心的距离均值总和最短**。因此,K-means聚类算法具体的计算步骤如下:
|
|||
|
|
|
|||
|
|
1. 随机选择k个节点,作为初始的k个聚类的中心;
|
|||
|
|
2. 针对所有的节点,计算它们和k个聚类中心的距离,将节点归入离它最近的类中;
|
|||
|
|
3. 针对k个类,统计每个类内节点的向量均值,作为每个类的新的中心向量;
|
|||
|
|
4. 重复第2步和第3步,**重新计算每个节点和新的类中心的距离,将节点再次划分到最近的类中,然后再更新类的中心节点向量**。经过多次迭代,直到节点分类不再变化,或者迭代次数达到上限,我们停止算法。
|
|||
|
|

|
|||
|
|
|
|||
|
|
以上,就是K-means聚类算法的计算过程了,那使用聚类算法代替了局部敏感哈希以后,我们该怎么进行相似检索呢?
|
|||
|
|
|
|||
|
|
## 如何使用聚类算法进行相似检索?
|
|||
|
|
|
|||
|
|
首先,对于所有的数据,我们先用聚类算法将它们划分到不同的类中。在具体操作之前,我们会给聚类的个数设定一个目标。假设聚类的个数是1024个,那所有的点就会被分到这1024个类中。这样,我们就可以用每个聚类的ID作为Key,来建立倒排索引了。
|
|||
|
|
|
|||
|
|
建立好索引之后,当要查询一个点邻近的点时,我们直接计算该点和所有聚类中心的距离,将离查询点最近的聚类作为该点所属的聚类。因此,以该聚类的ID为Key去倒排索引中查询,我们就可以取出所有该聚类中的节点列表了。然后,我们遍历整个节点列表,计算每个点和查询点的距离,取出Top K个结果进行返回。
|
|||
|
|
|
|||
|
|
这个过程中会有两种常见情况出现。第一种,最近的聚类中的节点数非常多。这个时候,我们就计算该聚类中的所有节点和查询点的距离,这个代价会很大。这该怎么优化呢?这时,我们可以参考二分查找算法不断划分子空间划分的思路,使用层次聚类将一个聚类中的节点,再次划分成多个聚类。这样,在该聚类中查找相近的点时,我们通过继续判断查询点和哪个子聚类更相近,就能快速减少检索空间,从而提升检索效率了。
|
|||
|
|

|
|||
|
|
|
|||
|
|
第二种,该聚类中的候选集不足Top K个,或者我们担心聚类算法的相似判断不够精准,导致最近的聚类中的结果不够好。那我们还可以再去查询次邻近的聚类,将这些聚类中的候选集取出,计算每个点和查询点的距离,补全最近的Top K个点。
|
|||
|
|
|
|||
|
|
## 如何使用乘积量化压缩向量?
|
|||
|
|
|
|||
|
|
对于向量的相似检索,除了检索算法本身以外,如何优化存储空间也是我们必须要关注的一个技术问题。以1024维的向量为例,因为每个向量维度值是一个浮点数(浮点数就是小数,一个浮点数有4个字节),所以一个向量就有4K个字节。如果是上亿级别的数据,光是存储向量就需要几百G的内存,这会导致向量检索难以在内存中完成检索。
|
|||
|
|
|
|||
|
|
因此,为了能更好地将向量加载到内存中,我们需要压缩向量的表示。比如说,我们可以用聚类中心的向量代替聚类中的每个向量。这样,一个类内的点都可以用这个类的ID来代替和存储,我们也就节省了存储每个向量的空间开销。那计算查询向量和原始样本向量距离的过程,也就可以改为计算查询向量和对应聚类中心向量的距离了。
|
|||
|
|

|
|||
|
|
|
|||
|
|
想要压缩向量,我们往往会使用**向量量化**(Vector Quantization)技术。其中,我们最常用的是**乘积量化**(Product Quantization)技术。
|
|||
|
|
|
|||
|
|
乍一看,你会觉得乘积量化是个非常晦涩难懂的概念,但它其实并没有那么复杂。接下来,我就把它拆分成乘积和量化这两个概念,来为你详细解释一下。
|
|||
|
|
|
|||
|
|
**量化指的就是将一个空间划分为多个区域,然后为每个区域编码标识**。比如说,一个二维空间<x,y>可以被划为两块,那我们只需要1个比特位就能分别为这两个区域编码了,它们的空间编码分别是0和1。那对二维空间中的任意一个点来说,它要么属于区域0,要么属于区域1。
|
|||
|
|
|
|||
|
|
这样,我们就可以用1个比特位的0或1编码,来代替任意一个点的二维空间坐标<x,y>了 。假设x和y是两个浮点数,各4个字节,那它们一共是8个字节。如果我们将8个字节的坐标用1个比特位来表示,就能达到压缩存储空间的目的了。前面我们说的用聚类ID代替具体的向量来进行压缩,也是同样的原理。
|
|||
|
|
|
|||
|
|
而**乘积指的是高维空间可以看作是由多个低维空间相乘得到的**。我们还是以二维空间<x,y>为例,它就是由两个一维空间和相乘得到。类似的还有,三维空间<x,y,z>是由一个二维空间<x,y>和一个一维空间相乘得到,依此类推。
|
|||
|
|
|
|||
|
|
那将高维空间分解成多个低维空间的乘积有什么好处呢?它能降低数据的存储量。比如说,二维空间是由一维的x轴和y轴相乘得到。x轴上有4个点x1到x4,y轴上有4个点y1到y4,这四个点的交叉乘积,会在二维空间形成16个点。但是,如果我们仅存储一维空间中,x轴和y轴的各4个点,一共只需要存储8个一维的点,这会比存储16个二维的点更节省空间。
|
|||
|
|
|
|||
|
|
总结来说,对向量进行乘积量化,其实就是将向量的高维空间看成是多个子空间的乘积,然后针对每个子空间,再用聚类技术分成多个区域。最后,给每个区域生成一个唯一编码,也就是聚类ID。
|
|||
|
|
|
|||
|
|
好了,乘积量化压缩向量的原理我们已经知道了。接下来,我们就通过一个例子来说说,乘积量化压缩样本向量的具体操作过程。
|
|||
|
|
|
|||
|
|
如果我们的样本向量都是1024维的浮点数向量,那我们可以将它分为4段,这样每一段就都是一个256维的浮点向量。然后,在每一段的256维的空间里,我们用聚类算法将这256维空间再划分为256个聚类。接着,我们可以用1至256作为ID,来为这256个聚类中心编号。这样,我们就得到了256 \* 4 共1024个聚类中心,每个聚类中心都是一个256维的浮点数向量(256 \* 4字节 = 1024字节)。最后,我们将这1024个聚类中心向量都存储下来。
|
|||
|
|

|
|||
|
|
|
|||
|
|
这样,对于这个空间中的每个向量,我们就不需要再精确记录它在每一维上的权重了。我们只需要将每个向量都分为四段,让**每段子向量都根据聚类算法找到所属的聚类,然后用它所属聚类的ID来表示这段子向量**就可以了。
|
|||
|
|
|
|||
|
|
因为聚类ID是从1到256的,所以我们只需要8个比特位就可以表示这个聚类ID了。由于完整的样本向量有四段,因此我们用4个聚类ID就可以表示一个完整的样本向量了,也就一共只需要32个比特位。因此,一个1024维的原始浮点数向量(共1024 \* 4 字节)使用乘积量化压缩后,存储空间变为了32个比特位,空间使用只有原来的1/1024。存储空间被大幅降低之后,所有的样本向量就有可能都被加载到内存中了。
|
|||
|
|

|
|||
|
|
|
|||
|
|
## 如何计算查询向量和压缩样本向量的距离(相似性)?
|
|||
|
|
|
|||
|
|
这样,我们就得到了一个压缩后的样本向量,它是一个32个比特位的向量。这个时候,如果要我们查询一个新向量和样本向量之间的距离,也就是它们之间的相似性,我们该怎么做呢?这里我要强调一下,一般来说,要查询的新向量都是一个未被压缩过的向量。也就是说在我们的例子中,它是一个1024维的浮点向量。
|
|||
|
|
|
|||
|
|
好了,明确了这一点之后,我们接着来说一下计算过程。这整个计算过程会涉及3个主要向量,分别是**样本向量**、**查询向量**以及**聚类中心向量**。你在理解这个过程的时候,要注意分清楚它们。
|
|||
|
|
|
|||
|
|
那接下来,我们一起来看一下具体的计算过程。
|
|||
|
|
|
|||
|
|
首先,我们在对所有样本点生成聚类时,需要记录下**聚类中心向量**的向量值,作为后面计算距离的依据。由于1024维向量会分成4段,每段有256个聚类。因此,我们共需要存储1024个聚类中所有中心向量的数据。
|
|||
|
|
|
|||
|
|
然后,对于**查询向量**,我们也将它分为4段,每段也是一个256维的向量。对于查询向量的每一段子向量,我们要分别计算它和之前存储的对应的256个聚类中心向量的距离,并用一张距离表存下来。由于有4段,因此一共有4个距离表。
|
|||
|
|

|
|||
|
|
|
|||
|
|
当计算查询向量和样本向量的距离时,我们将查询向量和样本向量都分为4段子空间。然后分别计算出每段子空间中,查询子向量和样本子向量的距离。这时,我们可以用聚类中心向量代替样本子向量。这样,求查询子向量和样本子向量的距离,就转换为求查询子向量和对应的聚类中心向量的距离。那我们只需要将样本子向量的聚类ID作为key去查距离表,就能在O(1)的时间代价内知道这个距离了。
|
|||
|
|

|
|||
|
|
|
|||
|
|
最后,我们将得到的四段距离按欧氏距离的方式计算,合并起来,即可得到查询向量和样本向量的距离,距离计算公式:
|
|||
|
|
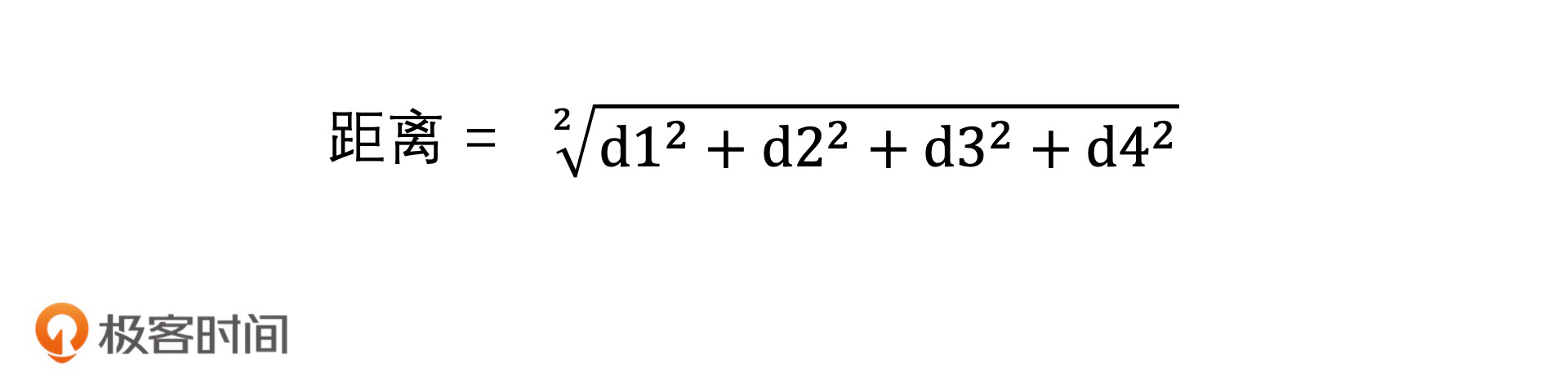
|
|||
|
|
|
|||
|
|
以上,就是计算查询向量和样本向量之间距离的过程了。你会看到,原本两个高维向量的复杂的距离计算,被4次O(1)时间代价的查表操作代替之后,就变成了常数级的时间代价。因此,在对压缩后的样本向量进行相似查找的时候,我们即便是使用遍历的方式进行计算,时间代价也会减少许多。
|
|||
|
|
|
|||
|
|
而计算查询向量到每个聚类中心的距离,我们也只需要在查询开始的时候计算一次,就可以生成1024个距离表,在后面对比每个样本向量时,这个对比表就可以反复使用了。
|
|||
|
|
|
|||
|
|
## 如何对乘积量化进行倒排索引?
|
|||
|
|
|
|||
|
|
尽管使用乘积量化的方案,我们已经可以用很低的代价来遍历所有的样本向量,计算每个样本向量和查询向量的距离了。但是我们依然希望能用更高效的检索技术代替遍历,来提高检索效率。因此,结合前面的知识,我们可以将聚类、乘积量化和倒排索引综合使用,让整体检索更高效。下面,我就来具体说说,在建立索引和查询这两个过程中,它们是怎么综合使用的。
|
|||
|
|
|
|||
|
|
首先,我们来说建立索引的过程,我把它总结为3步。
|
|||
|
|
|
|||
|
|
1. 使用K-means聚类,将所有的样本向量分为1024个聚类,以聚类ID为Key建立倒排索引。
|
|||
|
|
2. 对于每个聚类中的样本向量,计算它们和聚类中心的差值,得到新的向量。你也可以认为这是以聚类中心作为原点重新建立向量空间,然后更新该聚类中的每个样本向量。
|
|||
|
|
3. 使用乘积量化的方式,压缩存储每个聚类中新的样本向量。
|
|||
|
|

|
|||
|
|
|
|||
|
|
建好索引之后,我们再来说说查询的过程,它也可以总结为3步。
|
|||
|
|
|
|||
|
|
1. 当查询向量到来时,先计算它离哪个聚类中心最近,然后查找倒排表,取出该聚类中所有的向量。
|
|||
|
|
2. 计算查询向量和聚类中心的差值,得到新的查询向量。
|
|||
|
|
3. 对新的查询向量,使用乘积量化的距离计算法,来遍历该聚类中的所有压缩样本向量,取出最近的k个结果返回。
|
|||
|
|

|
|||
|
|
|
|||
|
|
这样,我们就同时结合了聚类、乘积量化和倒排索引的检索技术,使得我们能在压缩向量节省存储空间的同时,也通过快速减少检索空间的方式,提高了检索效率。通过这样的组合技术,我们能解决大量的图片检索问题。比如说,以图搜图、拍照识物,人脸识别等等。
|
|||
|
|
|
|||
|
|
实际上,除了图像检索领域,在文章推荐、商品推荐等推荐领域中,我们也都可以用类似的检索技术,来快速返回大量的结果。尤其是随着AI技术的发展,越来越多的对象需要用特征向量来表示。所以,针对这些对象的检索问题,其实都会转换为高维空间的近似检索问题,那我们今天讲的内容就完全可以派上用场了。
|
|||
|
|
|
|||
|
|
## 重点回顾
|
|||
|
|
|
|||
|
|
今天,我们学习了在高维向量空间中实现近似最邻近检索的方法。相对于局部敏感哈希,使用聚类技术能实现更灵活的分类能力,并且聚类技术还支持层次聚类,它能更快速地划分检索空间。
|
|||
|
|
|
|||
|
|
此外,对于高维的向量检索,如何优化存储空间也是我们需要考虑的一个问题。这个时候,可以使用乘积量化的方法来压缩样本向量,让我们能在内存中运行向量检索的算法。
|
|||
|
|
|
|||
|
|
那为了进一步提高检索率和优化存储空间,我们还能将聚类技术、乘积量化和倒排索引技术结合使用。这也是目前图像检索和文章推荐等领域中,非常重要的设计思想和实现方案。
|
|||
|
|

|
|||
|
|
|
|||
|
|
## 课堂讨论
|
|||
|
|
|
|||
|
|
1.为什么使用聚类中心向量来代替聚类中的样本向量,我们就可以达到节省存储空间的目的?
|
|||
|
|
|
|||
|
|
2.如果二维空间中有16个点,它们是由x轴的1、2、3、4四个点,以及y轴的1、2、3、4四个点两两相乘组合成的。那么,对于二维空间中的这16个样本点,如果使用乘积量化的思路,你会怎么进行压缩存储?当我们新增了一个点(17,17)时,它的查询过程又是怎么样的?
|
|||
|
|
|
|||
|
|
欢迎在留言区畅所欲言,说出你的思考过程和最终答案。如果有收获,也欢迎把这一讲分享给你的朋友。
|
|||
|
|
|