116 lines
12 KiB
Markdown
116 lines
12 KiB
Markdown
|
|
# 05 | 直方图与幂分布:为什么全世界1%的人掌握着50%的财富?
|
|||
|
|
|
|||
|
|
数据给你一双看透本质的眼睛,这里是《数据分析思维课》,我是郭炜。
|
|||
|
|
|
|||
|
|
我们之前讲了各种从数据结论中去伪存真的办法,我们今天更进一步,来看看当数据摆在你面前的时候,你应该如何从数据当中发现特征?
|
|||
|
|
|
|||
|
|
今天我就教给你一个最简单的办法——直方图。
|
|||
|
|
|
|||
|
|
你可能会有类似这样的想法:直方图还不简单,不就是柱状图吗?一个Excel就搞定了,我天天画柱状图。
|
|||
|
|
|
|||
|
|
但这种想法是错误的,因为直方图并不等于柱状图。现在请你花一分钟时间,仔细看看下面这两个图表,你能分辨出哪个是直方图,哪个是柱状图吗?
|
|||
|
|
|
|||
|
|

|
|||
|
|
|
|||
|
|

|
|||
|
|
|
|||
|
|
## 直方图与柱状图
|
|||
|
|
|
|||
|
|
答案是第一个图(动物园平均参观时长)为直方图,第二个图(动物园平均参观人数)为柱状图。
|
|||
|
|
|
|||
|
|
看上去上面这两幅图都是用直直方方的图形来展示,但其实它们是两种完全不同的图形展现和数据分析方法。那问题来了,我们如何才能分清楚直方图和柱状图呢?
|
|||
|
|
|
|||
|
|
我教你一个最简单的办法:**直方图是展示数据的分布,而柱状图是比较数据的大小。**
|
|||
|
|
|
|||
|
|
更具体点来说,直方图的X轴是定量的数据或者区域数据(用于看分布),而柱状图X轴是分类的数据。就拿刚刚的这两个图来说,第一个图其实是 X轴是**人们观光动物园的时间分布**,而第二个图的X轴是**人们去动物园场馆的具体分类**。
|
|||
|
|
|
|||
|
|
直方图是针对定量数据分布的定性分析,柱状图是对分类数据的定量数据分析,这两兄弟长得很像,用途也是互为补充。在第一个图里你能看到有40%的游客是停留了4个小时,但无法知道每天有多少游客去动物园。而在第二个图里,你能够知道大概每天会有95万名游客去了熊猫馆,但不能够看到游客的游览时间分布情况。
|
|||
|
|
|
|||
|
|
你也可以从表现形式上来对直方图与柱状图加以区分。
|
|||
|
|
|
|||
|
|
从柱子的间隔上来说,直方图的柱子和柱子之间没有间隔,而柱状图之间柱子是有间隔的。从柱子的宽度上来讲,直方图的柱子宽度可以不一样,而柱状图的柱子宽度必须一样。
|
|||
|
|
|
|||
|
|
对直方图来说,它的柱子宽度代表区间的长度,根据区间的不同,柱子宽度可以不同。但柱状图的柱子宽度没有数值含义,所以宽度必须一致。你可以看看下面的这张图,这是美国人口普查局(The U.S. Census Bureau)调查12.4亿人的上班通勤时间的直方图,最后右侧的直方柱子就像一个矮胖子一样,直接蹲在地板上了。
|
|||
|
|
|
|||
|
|

|
|||
|
|
|
|||
|
|
## 神奇的直方图
|
|||
|
|
|
|||
|
|
教你分辨完直方图与柱状图后,我们再来聊聊直方图。直方图最早是由数据统计学家Karl Pearson在1891年引入,它可以用来统计现实生活中各种各样的数据分布情况。
|
|||
|
|
|
|||
|
|
那具体直方图我们要怎么使用呢?你在搞不清楚某些数据的情况的时候。就可以把它画成一个直方图,然后就能够看到其中的规律了。举个例子,你可以看看[下面](https://raw.githubusercontent.com/owid/covid-19-data/master/public/data/vaccinations/vaccinations.csv)这组数据,这是来自2021年截至4月底,所有的新冠肺炎疫情国家的累计发病人数。
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
是不是如果只看这幅图,你会感觉满屏都是数字,不知道如何下手,更别说得出什么结论了。
|
|||
|
|
|
|||
|
|
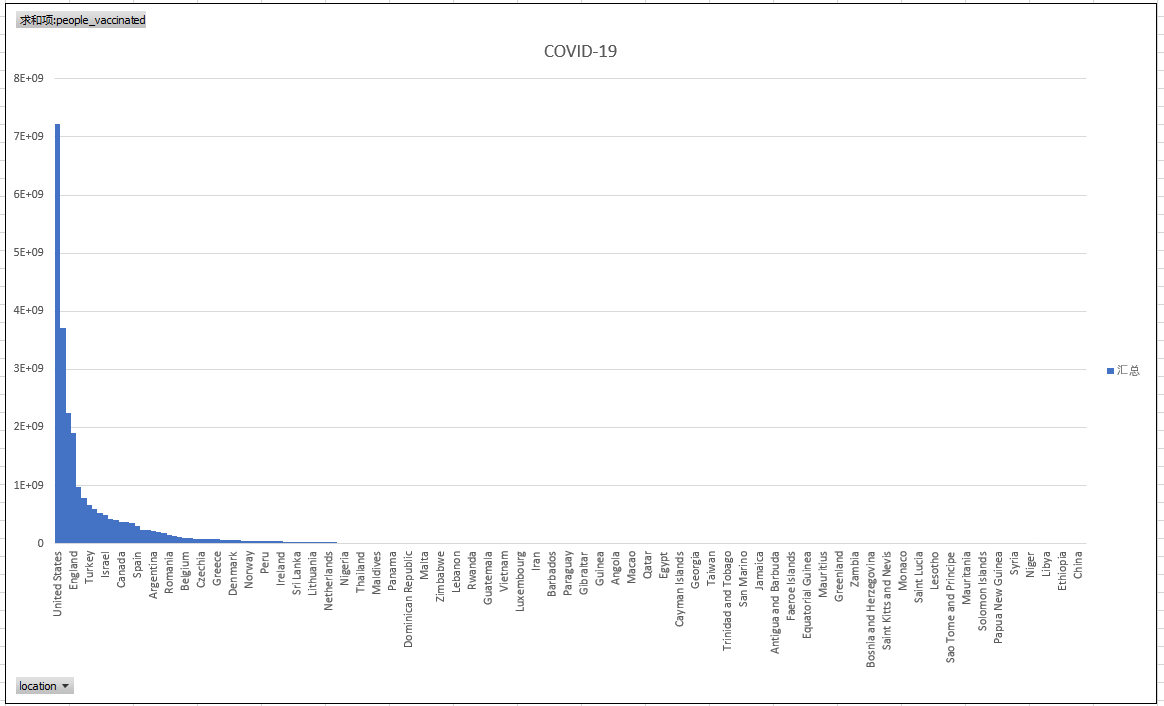
但是当我们用直方图把这些数字给表示出来的时候,神奇的事情发生了。你会清晰地发现,拿全球所有的国家这个范围来看,其实绝大部分的病例都发生在极少数的国家里,就像下面这幅图一样。
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
而且这样的分布并不是个例,我们现在把目光转向亚马逊丛林。
|
|||
|
|
|
|||
|
|
亚马逊地区有着全球树种最丰富的雨林,科学家已将亚马逊地区将近16000种树种编入物种目录。尽管亚马逊雨林呈现出如此多彩的物种多样性,科学家们还是发现在其中有227种树种牢牢占据主导地位,这些树种的分布面积几乎占到了整个亚马逊雨林面积的一半,也就是说仅1.4%的树种就占据了整个地区的50%,画出图来也和上面的图形类似。
|
|||
|
|
|
|||
|
|
这种从直方图体现出来呈指数下降或者上升的分布形式,科学家们把它叫做“幂律分布”。
|
|||
|
|
|
|||
|
|
## 幂律分布与帕累托法则
|
|||
|
|
|
|||
|
|
幂率分布也叫做指数分布,你会发现在这种分布里,X轴的开始的地方数值很高(或很低),然后以指数级的下降(或上升)到X轴的末尾段,按照统计学定义叫做:“分布密度函数是幂函数的分布”。
|
|||
|
|
|
|||
|
|
这样的规律其实无处不在,拿我们日常使用的词汇来说,你自己最常用的词汇往往就是那些500~1000个词,其余的词汇少量或者更少量在书面时候使用,如果你把你自己的用词数做一个直方图,你会发现语言的词汇使用率也是呈幂律分布的。
|
|||
|
|
|
|||
|
|
不止中文、英文,其实全球语言使用的词汇其实都是服从幂律分布的。所以我们在学外语的时候,经常看到要背会最常用的多少个单词。比如大学英语你去考4级6级8级,很多词汇书上会写着“超实用XX词速记”“XX词随身带”,这些词汇书就是基于语言的幂律分布,来帮助我们更好地学习外语。
|
|||
|
|
|
|||
|
|
那么这种现象是怎么产生的呢?
|
|||
|
|
|
|||
|
|
病毒、树种和语言其实都有一个共性——传播性。比如在亚马逊雨林里,两株植物长在了一块,那么每天这两株植物就要为阳光和土壤中的养分去竞争。如果其中一株能比另外一株植物每天稍微长快一点,那么它就能长得更高,从而获得更多的阳光、吸收更多的养分。
|
|||
|
|
|
|||
|
|
如果每天都有这些额外的能量,这株植物就更加有能力把种子给传播出去,然后复制这种模式。一直持续下去,这种植物就会积累出得天独厚的优势。
|
|||
|
|
|
|||
|
|
在语言的使用和病毒的传播当中也是同理。开始的微妙的优势会随着时间逐步加强,最后就能占领绝对优势,就像滚雪球一样,越滚越大。拿美国来说,它的医疗水平能力确实很强,但是由于美国对待疫情的态度并不够重视,病毒在美国其实是占据传播的优势的。所以强如美国,最后也被新冠给好好上了一课。
|
|||
|
|
|
|||
|
|
说到幂律分布,那就不得不提一下帕雷托法则了。你或许对帕累托法则有些陌生,但我要是说二八法则,你肯定听过。
|
|||
|
|
|
|||
|
|
二八法则简单来说,就是20%的人占了80%的资源,剩下80%的人分最后20%的资源。这个法则诞生于帕累托的花园。有一天帕累托偶然发现,自己园子里绝大部分的豌豆是由园子里极少部分豌豆荚产生。
|
|||
|
|
|
|||
|
|
作为一名擅长数学的经济学家,帕累托意识到这里面大有玄机。于是他马上把这种现象应用到了生活的其他领域,他惊奇地发现,意大利人80%的土地仅掌握在20%的手的人的手中,就和园子当中的豌豆荚类似,于是发表了著名的“帕雷托法则”(也被人称之为“二八法则”)。这个法则的背后的规律就是幂律分布。
|
|||
|
|
|
|||
|
|
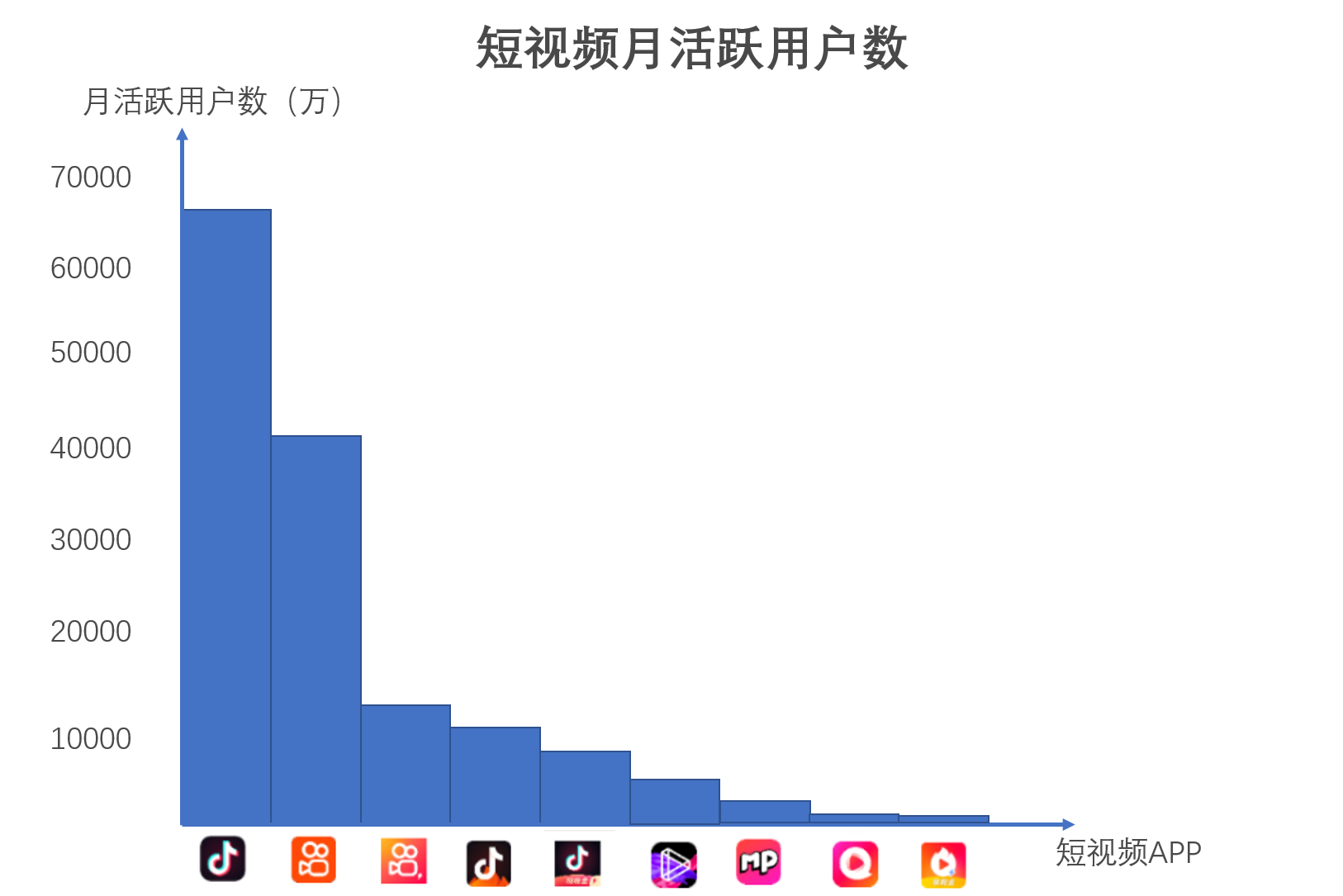
企业的竞争力也同样符合帕累托法则。举个例子,如果我们把全网短视频APP的月活用户用柱状图表示出来,你会发现同样符合幂律分布。就像文稿里的这张图这样,比较高的APP的月活会高于均值很多倍,第一名、第二名分掉了整体赛道流量的90%。所以在互联网领域里才会有这么一句话:一个领域只有第一、第二,没有第三。
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
幂律分布与帕累托法则其实都强调了重要的少数和琐碎的多数,从某种意义上来讲,世界从来都不是平衡的。
|
|||
|
|
|
|||
|
|
所以在日常生活里,不要把所有事都放在同一个优先级上,而是学会用帕累托法则去看待问题,找出最重要的20%的问题,并最优先解决。同时,你也要留个心眼:为什么这20%的问题对你来说最为重要?
|
|||
|
|
|
|||
|
|
对应到工作中,你可以多想想以下几个问题。
|
|||
|
|
|
|||
|
|
* 在你一天的工作分配当中,由于80%的工作都是日常反馈,你是否安排了自己最清醒的时间去处理最重要的20%工作?
|
|||
|
|
* 你所在的公司,是不是由20%的客户来为公司提供了80%的利润,如果是,应该如何留住这些客户?
|
|||
|
|
* 在团队里,杰出贡献是20%的人做的,80%的人是配合,那么针对这20%的人,你应该如何留住他们?
|
|||
|
|
* 能否通过弥补20%的质量缺口去获得80%的收益(或者避免80%的客户投诉)?
|
|||
|
|
* 在最有效的20%的时间内,如何引导团队做出80%的相关分析?
|
|||
|
|
|
|||
|
|
最后再来说说我们个人的发展。为什么有的人一开始和普通人差不多,但是他们后来渐渐地把同龄人甩在了身后?
|
|||
|
|
|
|||
|
|
有的人可能会觉得是因为这些人运气好,运气也是实力的一部分,但毕竟“幸运只光顾有准备的人”。你比其他人更努力,每天多积累1%哪怕是0.1%的优势,这样把优势不断积累下去,你就会占据越来越多的资源,成为这个领域里面的专家。
|
|||
|
|
|
|||
|
|
## 小结
|
|||
|
|
|
|||
|
|
好了,今天的课程到这里也就接近尾声了,我再来带你复习一下今天讲的内容。
|
|||
|
|
|
|||
|
|
今天我给你讲了两个重要的概念。一个是非常简单但有效的工具——直方图。直方图可以让你从混沌的数据里面找到其中的规律。很多的数据分布(包括下面几节课要讲的正态分布和拉普拉斯分布)都会用到这个工具。
|
|||
|
|
|
|||
|
|
紧接着我们从直方图讲到了幂律分布。这个统计学规律告诉我们,我们身处的世界是赢者通吃的世界,开始时细微优势最终将带来无穷多的回报。反之,最初的细微劣势也将导致最终一无所有。这个现象也有人称之为“马太效应”,在圣经《新约·马太福音》中是这样描述的:“ 凡有的,还要加给他,叫他多余。没有的,连他所有的也要夺过来 ”。
|
|||
|
|
|
|||
|
|
我们耳熟能详的帕雷托法则(也就是二八法则)、马太效应都是来自幂律分布。这个数字分布其实有很多点值得我们去思考,你可以尝试多在日常的工作以及生活里用一下它,或许能够给你一些意想不到的惊喜。
|
|||
|
|
|
|||
|
|
当然,帕累托法则给我带来最重要的一个认知更新是:每天在我们自己的专业领域里面,或者你的企业在所在的赛道里,只要你比其他人或者其他企业多成功1%,最终积累起来的竞争优势将使别人无法超越,你就会变成那个能够大声说“我全都要”的少数派。
|
|||
|
|
|
|||
|
|
不积跬步,无以至千里;不积小流,无以成江海。数据给你一双看透本质的眼睛,让我们每天在数据这个领域里面比别人多1%的认知,最终看到一个和别人完全不同的世界。我们一起学习数据的规律,一起共勉!
|
|||
|
|
|
|||
|
|
## 课后思考
|
|||
|
|
|
|||
|
|
在你的工作生活当中,还有哪些事情你觉得符合帕累托法则或者幂律分布?背后的原因是什么?分享出来,我们一起共同提高!
|
|||
|
|
|