108 lines
12 KiB
Markdown
108 lines
12 KiB
Markdown
|
|
# 01 | 平均值:不要被骗了,它不能代表整体水平
|
|||
|
|
|
|||
|
|
数据给你一双看透本质的眼睛,这里是《数据分析思维课》,我是郭炜。
|
|||
|
|
|
|||
|
|
我们在日常生活中经常会遇到这种情况,看到某些统计报告里面说,“某市的人均住房面积是120平米”“计算机行业人均年收入超过50万元”。你看完这个数据之后,倒吸一口凉气,然后去微博感叹:“对不起,我又给大家拖后腿了”“对不起,我又被幸福了”。
|
|||
|
|
|
|||
|
|
你不必为此焦虑,我只能奉劝你,以后看到这么不专业的统计报告就别看了。来,我带你看看准确客观的平均值统计应该是怎样的。首先,你得知道平均值究竟是什么。
|
|||
|
|
|
|||
|
|
从概念上看,平均值有很多种。单从数学上来说,就有算术平均值、几何平均值、平方平均值、调和平均值、加权平均值等等。所以当有人和你说平均值的时候,你要留个心眼问问他,你这说的是哪个平均值呀?
|
|||
|
|
|
|||
|
|
当然,我们日常生活中提到的平均值都默认是“**算术平均值**”,也就是“**一组数据中所有数据之和再除以数据的个数**”。这个概念不难理解,你在小学的时候就开始学了。不过看到这里,你可以先结合我们上面的例子想想,算术平均值有什么短板吗?
|
|||
|
|
|
|||
|
|
我先给一道极其简单的数学题,你可以先想想。我们有3个数,他们分别是0,1,20,这三个数的平均值不难算,是(0+1+20)/3=7,那7这个平均值和之前的三个数是不是差距挺大呢?是不是有些不客观呢?
|
|||
|
|
|
|||
|
|
所以,有的时候,平均值并不能代表整体水平。
|
|||
|
|
|
|||
|
|
## 平均值在什么情况下才有价值?
|
|||
|
|
|
|||
|
|
那平均值到底在什么情况下才有价值呢?回答这个问题之前,我再给你讲个故事。
|
|||
|
|
|
|||
|
|
昨天下楼的时候,我听到小区两个大妈在讨论,“这次期末考试,班里语文的平均分是71分,我孙子考了85分,厉不厉害!”在工作中,我偶尔也会听到同事说,“我们客户的平均客单价是1000元钱,竞争对手的只有500元,我们的客户比对方的高端多了。”这些说法都对吗?还真不一定。
|
|||
|
|
|
|||
|
|
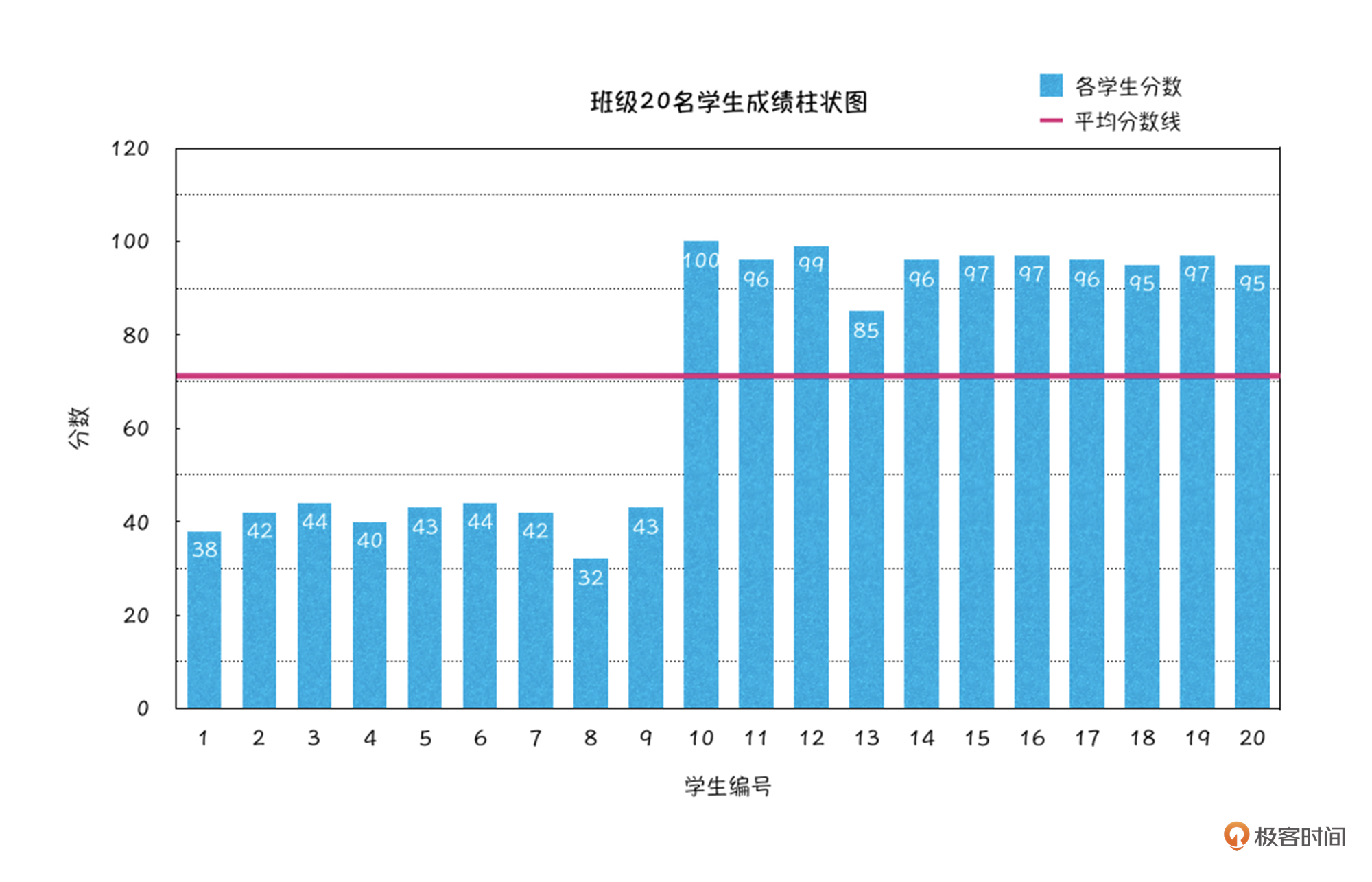
为了更好地解释这个问题,我先拿孩子的平均分给你举个例子。假设班级里20名学生的考试成绩如下图一样呈现两极分化的情况,一半孩子都在95分以上,还有近一半的孩子只有三四十分,我们很容易计算出这20名学生的成绩平均值是71.05(图中的红色直线)。
|
|||
|
|
|
|||
|
|
看上去孩子的85分比平均分71.05分高了很多,但你再仔细看,这个分数在好学生里其实是最差的那个,整体上看也只是班级中游水平。
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
同理,看上去这个企业的平均客单价很高——平均1000元,但如果你的数据是由1个1万元客户和10个100元的客户构成的(总收入11000元/11人=1000元/人),对方都是11个客单价500元的客户构成的,那么其实竞争对手才是真正的高客单价企业。
|
|||
|
|
|
|||
|
|
你可能会觉得我在抬杠,这些例子的数据集都太极端了吧?其实我是想说明一个问题:平均值是用所有样本数据计算的,**容易受到极端值的影响**。在不少情况下,平均值是没有价值的,它无法客观准确地反映数据整体情况。
|
|||
|
|
|
|||
|
|
更进一步来说,**整体平均值是在数据呈均匀分布或者正态分布的情况下才会有意义,如果忽略整个数据的分布情况,只提平均值,其实是没有意义的**。这也就是为什么你会在读一些统计分析报告时觉得自己不是“被加薪了”,就是“被幸福了”。
|
|||
|
|
|
|||
|
|
现在你明白了吗?在一些复杂情况下,我们是很难确定人群分布情况的,此时若直接使用平均数值,是很难反映整体真实情况的。
|
|||
|
|
|
|||
|
|
## 分组结论和整体平均值不是一回事
|
|||
|
|
|
|||
|
|
那怎么才能反映真实情况呢?
|
|||
|
|
|
|||
|
|
就拿平均薪水这个例子来说,你肯定有疑问:什么人啊?咋拿到那么多钱的?你肯定想看更详细的数据,诸如具体的岗位属性、工作年限、城市等等。有了这些信息,你才能知道你和人家的薪水差距到底差在哪了。
|
|||
|
|
|
|||
|
|
比如一个在一线城市工作3年的Java程序员的月平均工资是2万元,而我的月工资是1万元,那我确实是低一些,这个判断比起之前那个一刀切就准确太多了。
|
|||
|
|
|
|||
|
|
不知道你有没有注意到,在思考这个问题的过程中,你已经在不知不觉中引入了**分组**的逻辑。你应该也发现了,分组中的平均数和从整体中得到的平均数,是完全不一样的,分组中得到的平均数更具参考价值。
|
|||
|
|
|
|||
|
|
上面这个例子很好理解,我现在要顺着它抛出一个结论:**整体平均值不能代表各分组情况,分组结论和整体平均值结论可能会大相径庭。**
|
|||
|
|
|
|||
|
|
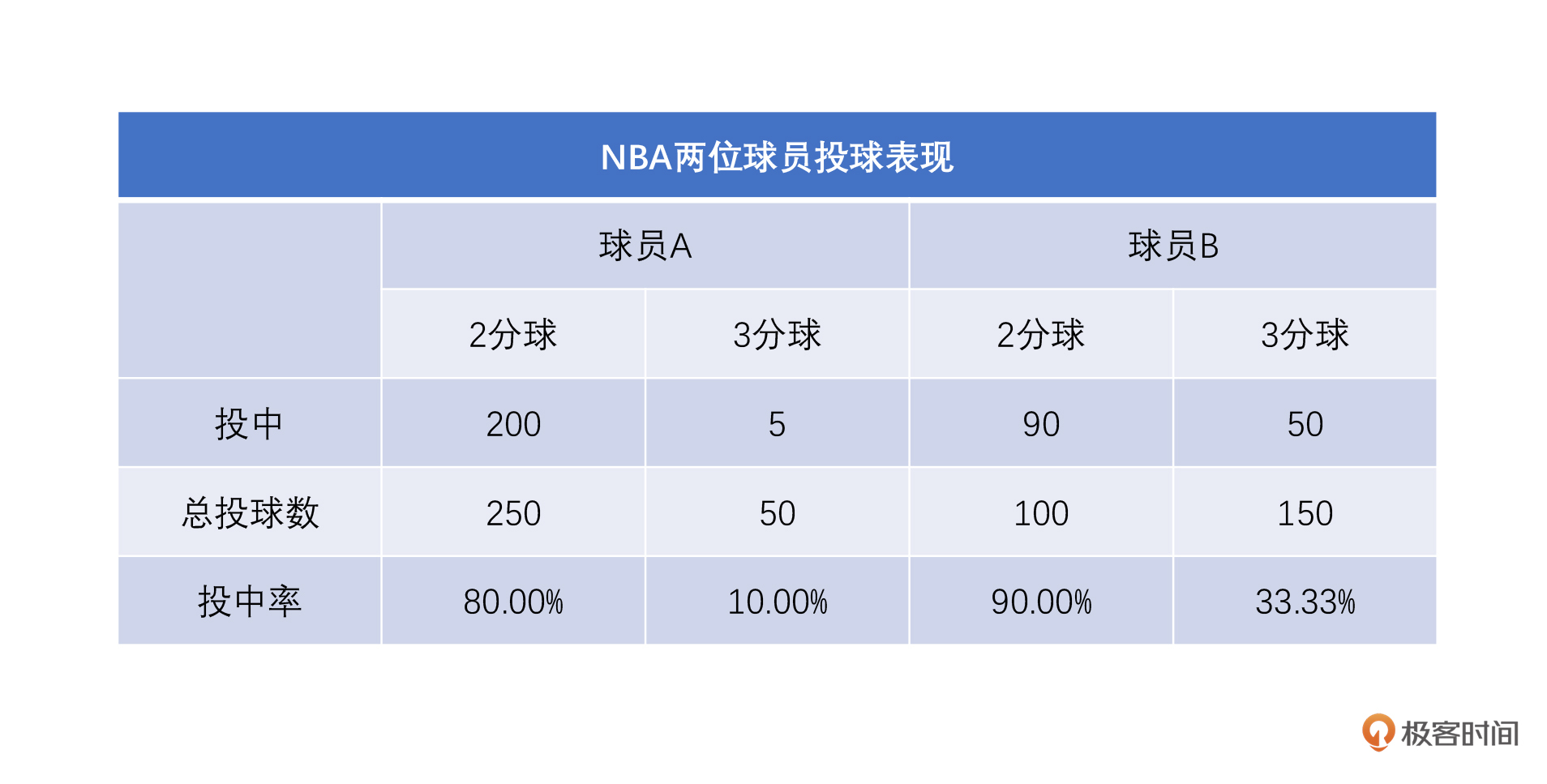
明白了吗?别急,我再讲一个例子反面论证一下这句话。话说NBA有两个球员,球员A和球员B,他们的投球的表现如下面这个图所示。
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
这里我简单描述下,先说2分球的情况:A球员,2分球总共投了250个,投中了200个,命中率80%;B球员,投了100个,投中了90个,命中率90%。也就是说,以2分球的命中率来看,B更牛一些。
|
|||
|
|
|
|||
|
|
投3分球的时候,A球员一共投了50个,投中5个,命中率10%;B球员,一共投了150个,投中50个,命中率33.33%。看来,无论2分球还是3分球,B都比A的投中率要高。看上去也是B比A厉害,对吧?
|
|||
|
|
|
|||
|
|
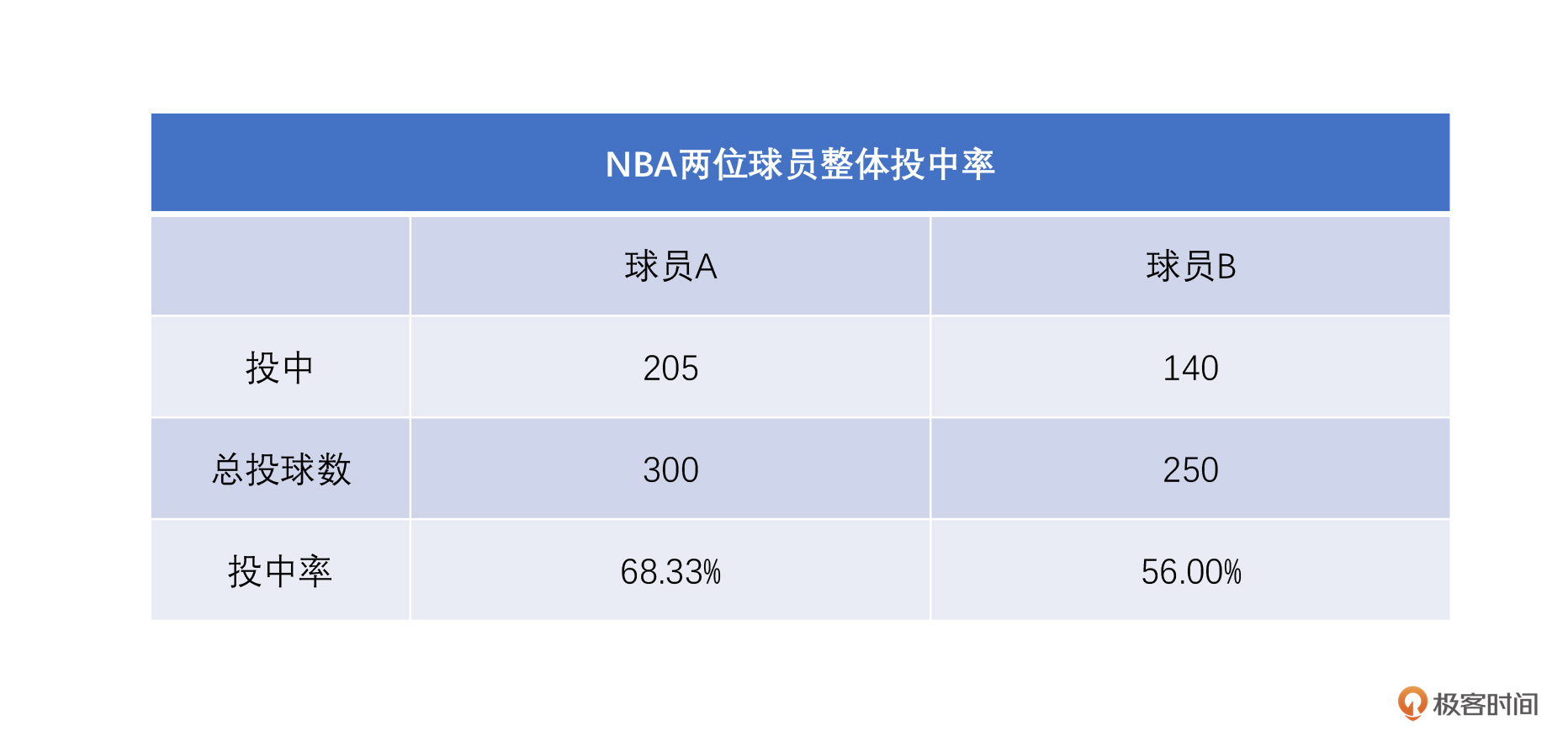
那问题就来了,可是从整体命中率来看好像不是这样啊。你看,如果我们算下两位球员的整体平均值(也就是整体投中率)。
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
A的总投球数是300个(250个2分球,50个3分球),共投中205个(200个2分球,5个3分球),投中率是68.33%;B呢,投了250个球,投中的两分和三分加到一起140个,那么他的投中率是56%,这么看来B比A的投中率68.33%要低呀。
|
|||
|
|
|
|||
|
|
看到这个结果,你是不是很诧异,不信你再仔细看看这个图表,我的确没有在数据上做手脚。
|
|||
|
|
|
|||
|
|
**两分球和三分球投中率都比较高的这个球员B,整体的命中率反而下降了**,是不是让人有点大跌眼镜?如果你是篮球爱好者,你应该会发现问题,NBA里没算过整体命中率,一般都是把二分球和三分球的命中率分开说的。
|
|||
|
|
|
|||
|
|
## 辛普森悖论的启示
|
|||
|
|
|
|||
|
|
为什么NBA不计算整体命中率呢?就是因为这样算不准确。这里我们可以引入一个著名的悖论——**辛普森悖论**,它讲的就是这个问题。辛普森悖论是1951年由E.H.辛普森提出的,简单来讲就是**在分组比较中都占优势的一方,有的时候在总评中反而是失势的一方。**
|
|||
|
|
|
|||
|
|
我用前面NBA球员命中率的例子跟你分析下产生辛普森悖论的原因。首先,两分球和三分球的投球能力根本不是一回事,这两个投球数本身就不应该相加;另外,B球员虽然厉害,但是他60%的球都是命中率比较低的三分球,而绝对数量上命中率较高的两分球投得就少了,而三分球的投中率是明显低于两分球的,这样就拉低了他的整体的投中率,造成了整体的劣势。
|
|||
|
|
|
|||
|
|
是不是还是有点绕?用一句话来讲,就是“质”(命中率)与“量”(投球数)是两个维度的数据,如果全部合并成“质”(命中率)这个维度的数据,那就会出错了。
|
|||
|
|
|
|||
|
|
再举一个例子,某游戏公司做了款游戏,有Android和iOS版本,而每个系统都有手机版本和Pad版本。一个数据分析师看完用户的付费数据后,发现整体上Android付费率比较高。他就直接告诉老板说,“你看我们Android的用户付费率要高于iOS的用户付费率,我们应该大力发展Android客户端!”这个数字是真实的,但是结论很可能是错误的。
|
|||
|
|
|
|||
|
|
因为我们再细分下去你会发现,这个数据分析师也是错误地把“质”(付费率)和“量”(用户数)简单合并,是一种想当然的行为。
|
|||
|
|
|
|||
|
|
因为还有可能出现这样一种情况:Android无论是平板还是手机的付费率分别都比iOS低,但是整体上因为安卓手机(注意,只是手机用户)的用户比较多,所以把Android付费率整体拉高了。但其实细分下去iOS、Pad和手机的付费率都比Android高,只是整体付费率低而已。你要是还有疑虑,可以对照上面NBA的例子,自己再推演一下。
|
|||
|
|
|
|||
|
|
**所以,我再来总结下,看到一个平均值的时候,你一定要留个心眼,看看它的数据构成情况,而不是简单地用平均值去代表所有的整体。**生活是具体的,如果你想看到更为准确的数据,你应该分组拆开来看。因为辛普森悖论告诉我们,有的时候,在分组比较中占优势的一方,在总评中反而可能是失势的一方。但你要注意,只是“有的时候”。
|
|||
|
|
|
|||
|
|
就像最近我看到一些文章,说税率改革之后我们的整体工资的税率反而是变高了,而不是变低了。这也是同一个道理,我们用整体的平均值去掩盖个体每一个不同区间段的税率变化,是不对的。我们应该更细分的数据去评定实际的好坏。
|
|||
|
|
|
|||
|
|
除此之外,辛普森悖论也给我们一个启示,就是:**每次小范围内的输赢,其实和你在整体上的输赢没有太大直接的关系。**这也是为什么在打麻将或者打德扑真正赢的那些人,不是那些小牌把把赢的人,而往往是赢一把大的人。
|
|||
|
|
|
|||
|
|
这也是这个辛普森悖论衍生出来的一个推论,将来你要用数据分析做决策的时候,小到打牌、大到做投资,不要过于计较局部的得失,而是要在关键时刻对大概率有把握的事情放手一搏。
|
|||
|
|
|
|||
|
|
## 小结
|
|||
|
|
|
|||
|
|
好了,今天这篇文章就到这里。我在最后再来给你串讲下这节课的知识点。
|
|||
|
|
|
|||
|
|
首先,当别人给你说平均值的时候,你要和他确认下说的是哪个平均值。当然,生活中,我们提到的平均值基本都是在说**算术平均值**。其次,算术平均值特别敏感,它很容易受到**极端数据**的影响,所以在很多选秀节目里,你经常会听到最后计算分数时要去掉一个最高分和一个最低分,这是一个道理。
|
|||
|
|
|
|||
|
|
你也一定要意识到,整体平均值是在**数据均匀分布或者正态分布**下才会有意义,如果忽略整个数据的分布情况,只提平均值是没有价值的。
|
|||
|
|
|
|||
|
|
最后,我和你聊了辛普森悖论。工作生活中,我们经常会遇到这样的悖论,甚至我见过很多传销人员就在用这个悖论在忽悠人,如果你遇到这样的案例,别忘了那句话:**分组结论和整体平均值结论可能会大相径庭**。
|
|||
|
|
|
|||
|
|
在我们的生活里,我们总提“质量”这个词,但是拆开来看,“质”与“量”是不等价的。所以当你不被大部分人所理解时,有可能是因为你选的路是一条少数人走的路。平均值和辛普森悖论告诉我们要抓大放小,不要因为某一个单项优势就洋洋得意,也不要因为局部失败就一蹶不振。生活,要有一颗平常心,我们的目标是让我们这一生的“人生平均值”逐步提高。
|
|||
|
|
|
|||
|
|
数据给你一双看透本质的双眼,让我们持续学习,持续提高。
|
|||
|
|
|
|||
|
|
## 课后思考
|
|||
|
|
|
|||
|
|
最后我给你留一个课后思考题:你在你的生活里,你还遇到过哪些平均值和辛普森悖论的例子吗?欢迎你分享出来,我们一块讨论。
|
|||
|
|
|
|||
|
|
欢迎在留言区与我分享你的想法,也欢迎你在留言区记录你的思考过程,如果你能有其他案例,那就更好了。感谢阅读,如果你觉得这篇文章对你有帮助的话,也欢迎把它分享给更多的朋友。
|
|||
|
|
|