176 lines
17 KiB
Markdown
176 lines
17 KiB
Markdown
|
|
# 03|缩放算法:如何高质量地缩放图像?
|
|||
|
|
|
|||
|
|
你好,我是李江。
|
|||
|
|
|
|||
|
|
今天,我们一起来聊聊图像的缩放算法。图像的缩放算法在我们的日常生活中使用非常频繁,只是可能你没有留意到。举个例子,你使用网页或者播放器看电影的时候,经常会开启全屏或者退出全屏,电影的播放画面就会变大,或者变小。这个过程里面就会用到图像的缩放算法。
|
|||
|
|
|
|||
|
|
事实上,只要视频的原始分辨率和播放窗口的大小不一致,就需要通过缩放处理来使得视频画面适应窗口的大小。比如说,电影分辨率是1080P,播放器的窗口大小是720P,则需要将电影画面从1080P缩小到720P再播放。如果你点击全屏播放,播放窗口变成了4K,则需要将电影画面做放大处理,即放大到4K之后再播放。这就是一个非常典型的图像缩放的例子。
|
|||
|
|
|
|||
|
|
在视频开发的过程中,图像的缩放就更多了。下面我列举3种用到图像缩放的情形:
|
|||
|
|
|
|||
|
|
* 情形1:播放窗口与原始图像分辨率不匹配的时候需要缩放。这和我刚才举的例子是一样的情况。
|
|||
|
|
* 情形2:我们在线观看视频时会有多种分辨率可以选择,即需要在一个图像分辨率的基础上缩放出多种不同尺寸的图像出来做编码,并保存多个不同分辨率的视频文件。
|
|||
|
|
* 情形3:RTC场景,有的时候我们需要根据网络状况实时调节视频通话的分辨率。这个也是需要缩放算法来完成的。
|
|||
|
|
|
|||
|
|
所以,我们可以看到图像的缩放算法是一个很常用的技术,且它是非常重要的。并且,由于图像的缩放会严重影响我们视觉的主观感受,所以图像缩放算法的选择也是非常重要的。目前图像的缩放算法非常多,其中主要包括最常用的插值算法和目前比较火的AI超分算法。
|
|||
|
|
|
|||
|
|
由于目前绝大多数图像的缩放还是通过插值算法来实现的,所以我们今天主要来聊聊插值算法。插值算法有很多种,但是其基本原理都是差不多的。**它们都是使用周围已有的像素值通过一定的加权运算得到“插值像素值”**。插值算法主要包括:最近邻插值算法(Nearest)、双线性插值算法(Bilinear)、双三次插值算法(BiCubic)等。那么在一一讲解这些插值算法之前,我们不妨先来聊聊缩放算法的基本原理。
|
|||
|
|
|
|||
|
|
## 缩放的基本原理
|
|||
|
|
|
|||
|
|
前面我们讲过,**图像的缩放就是将原图像****的****已有像素经过加权运算得到目标图像的目标像素**。
|
|||
|
|
|
|||
|
|
什么意思呢?比如说,我们已有图像是720P的分辨率,称之为原图像,我们需要放大到1080P,我们称这个1080P图像是目标图像。目标图像在宽度方向上放大了1920 / 1280 = 1.5倍,高度方向上也放大了1080 / 720 = 1.5倍。
|
|||
|
|
|
|||
|
|
**那怎么通过720P的原图像生成1080P的目标图像呢?**我们先将目标图像的像素位置映射到原图像的对应位置上,然后把通过插值计算得到的原图像对应位置的像素值作为目标图像相应位置的像素值。是不是有点绕?别急,下面我给你举个例子,通过它你就可以更直观地理解这句话的意思了。
|
|||
|
|
|
|||
|
|
比如说,1080P目标图像中的(0,0)位置就映射到720P原图像的(0,0)位置,取原图像(0,0)位置的像素值作为目标图像(0,0)位置的像素值。目标图像的(1,1)位置就映射到原图像中的(0.67, 0.67)位置。最后,通过原图像已有像素插值得到(0.67,0.67)位置的像素值,并将该像素值作为目标图像(1,1)位置的像素值。
|
|||
|
|
|
|||
|
|
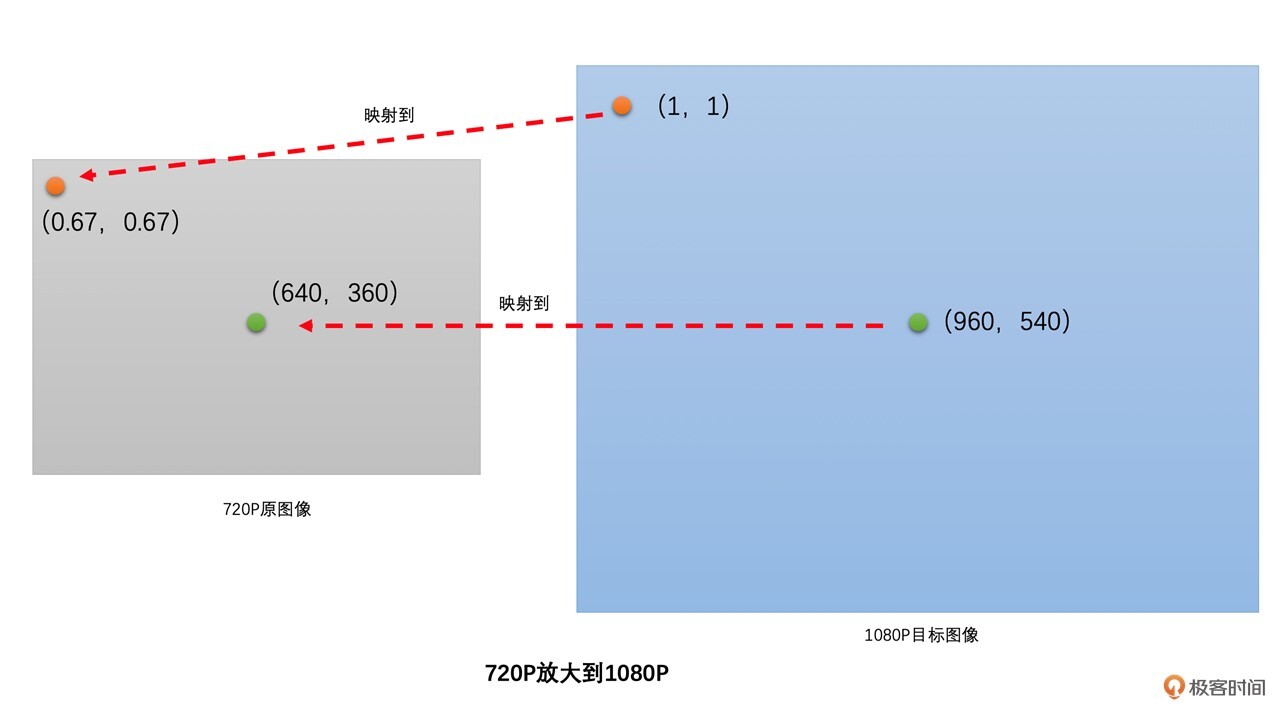
|
|||
|
|
|
|||
|
|
现在你知道了图像放大的大体过程,那图像缩小的过程是怎样的呢?
|
|||
|
|
|
|||
|
|
同样的我们以720P作为原图像,那么720P缩小到目标图像360P的过程也是类似于图像放大的过程的,这里通过下图描述一下映射的过程,具体就不重复了。
|
|||
|
|
|
|||
|
|
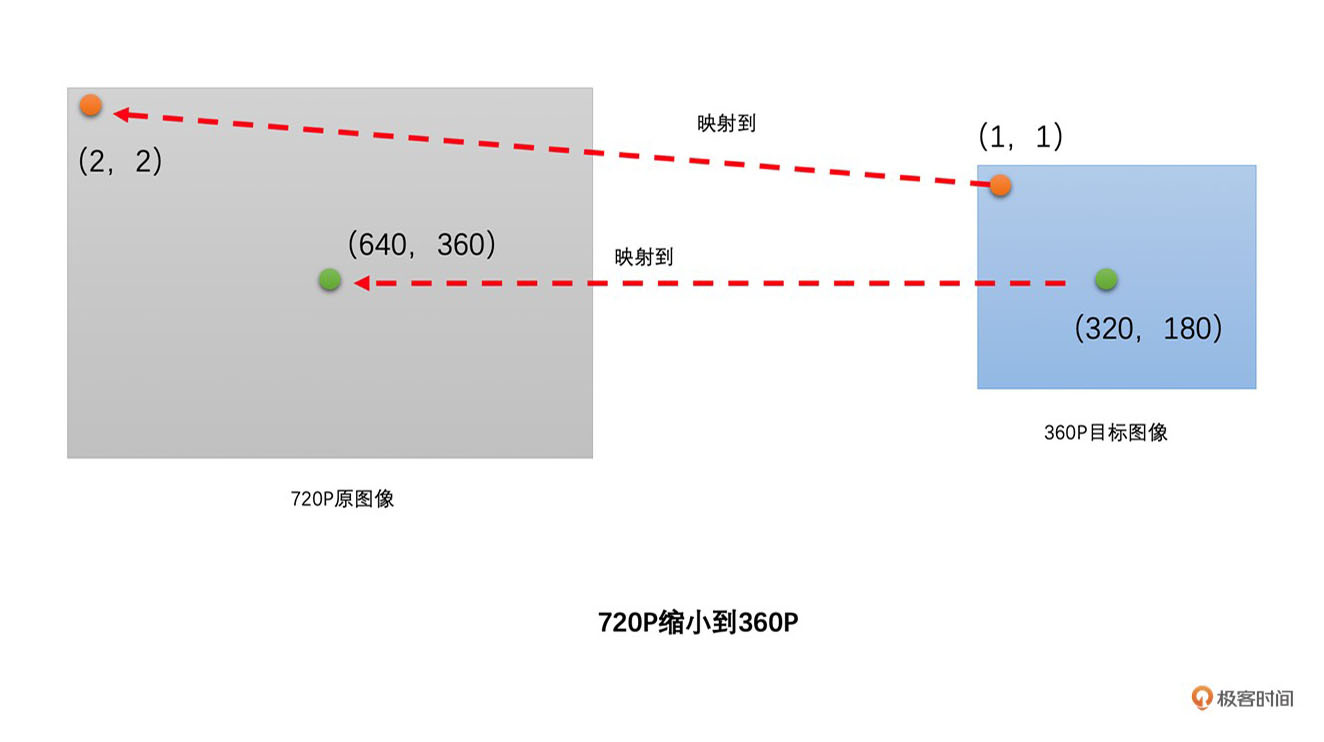
|
|||
|
|
好了,现在我们再回顾一下图像缩放的过程。
|
|||
|
|
|
|||
|
|
首先是图像放大的过程,对于1080P目标图像中的每一个像素点(x,y),我们只需要将它映射到720P原图像的(x / 1.5,y / 1.5)位置,通过原图像已有的像素值插值得到(x / 1.5,y / 1.5)的像素值就可以了。我们遍历一下目标图像中的每一个像素点位置,都能找到他们在原图像中的映射位置,并通过插值求出映射位置的像素值,这样就可以得到目标图像了,从而也就达到了放大的目的。
|
|||
|
|
|
|||
|
|
图像缩小的过程也是类似的。对于360P目标图像中的每一个像素点(x,y),我们只需要将它映射到720P原图像的(x \* 2,y \* 2)位置,通过原图像已有的像素值插值得到(x \* 2,y \* 2)的像素值就可以了。
|
|||
|
|
|
|||
|
|
下面我们以更通用的表达式来表达一下缩放过程。
|
|||
|
|
|
|||
|
|
假设原图像的分辨率是w0 x h0,我们需要缩放到w1 x h1。那**我们只需要将目标图像中的像素位置(x,y)映射到原图像的(x \* w0 / w1,y \* h0 / h1),****再****插值得到这个像素值就可以了,这个插值得到的像素值就是目标图像像素点(x,y)的像素值**。注意,(x \* w0 / w1,y \* h0 / h1)绝大多数时候是小数。**这就是图像缩放算法原理的通用表达**。下面是图像放大和缩小的映射过程的示意图。
|
|||
|
|
|
|||
|
|
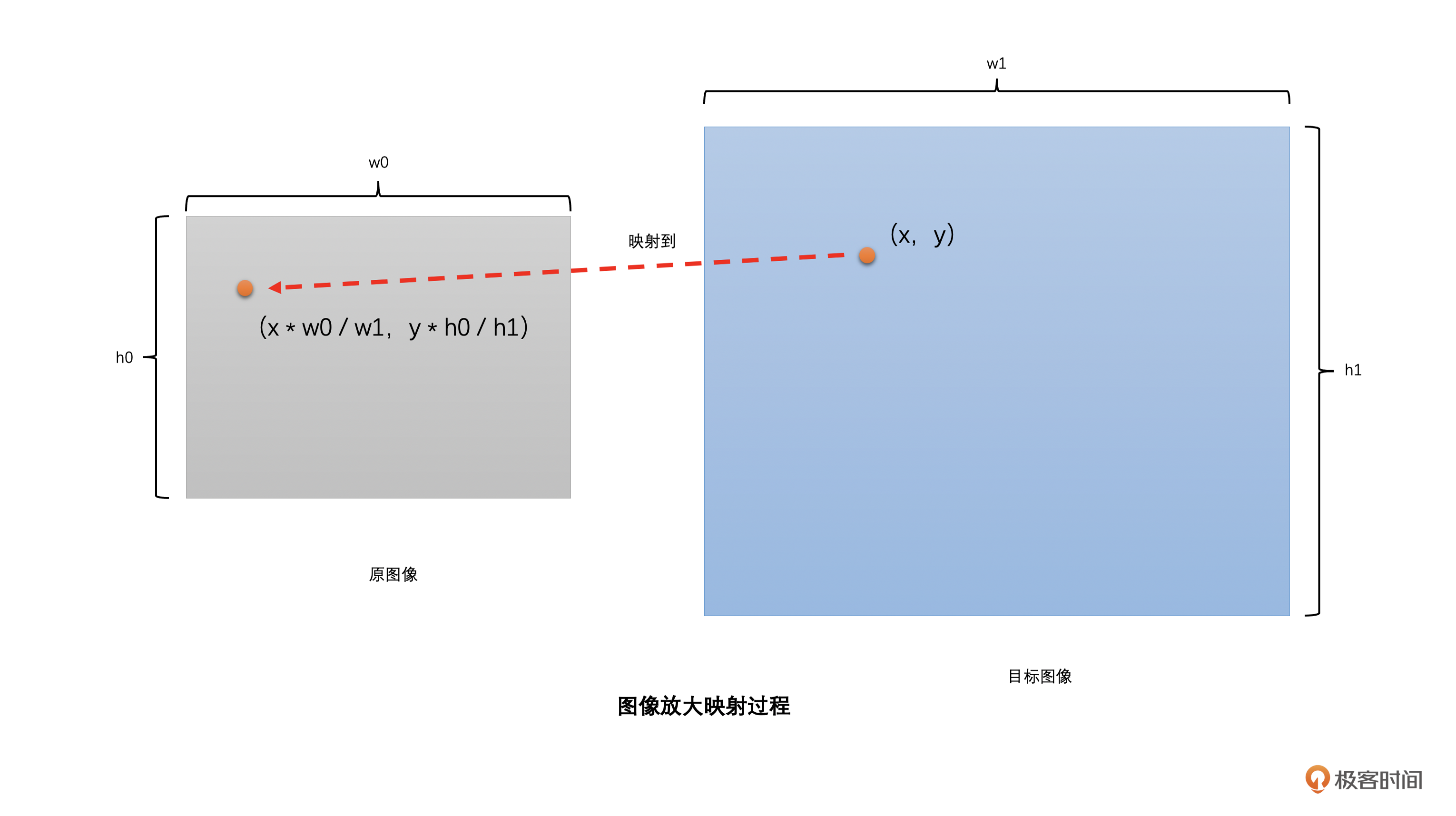
|
|||
|
|
|
|||
|
|
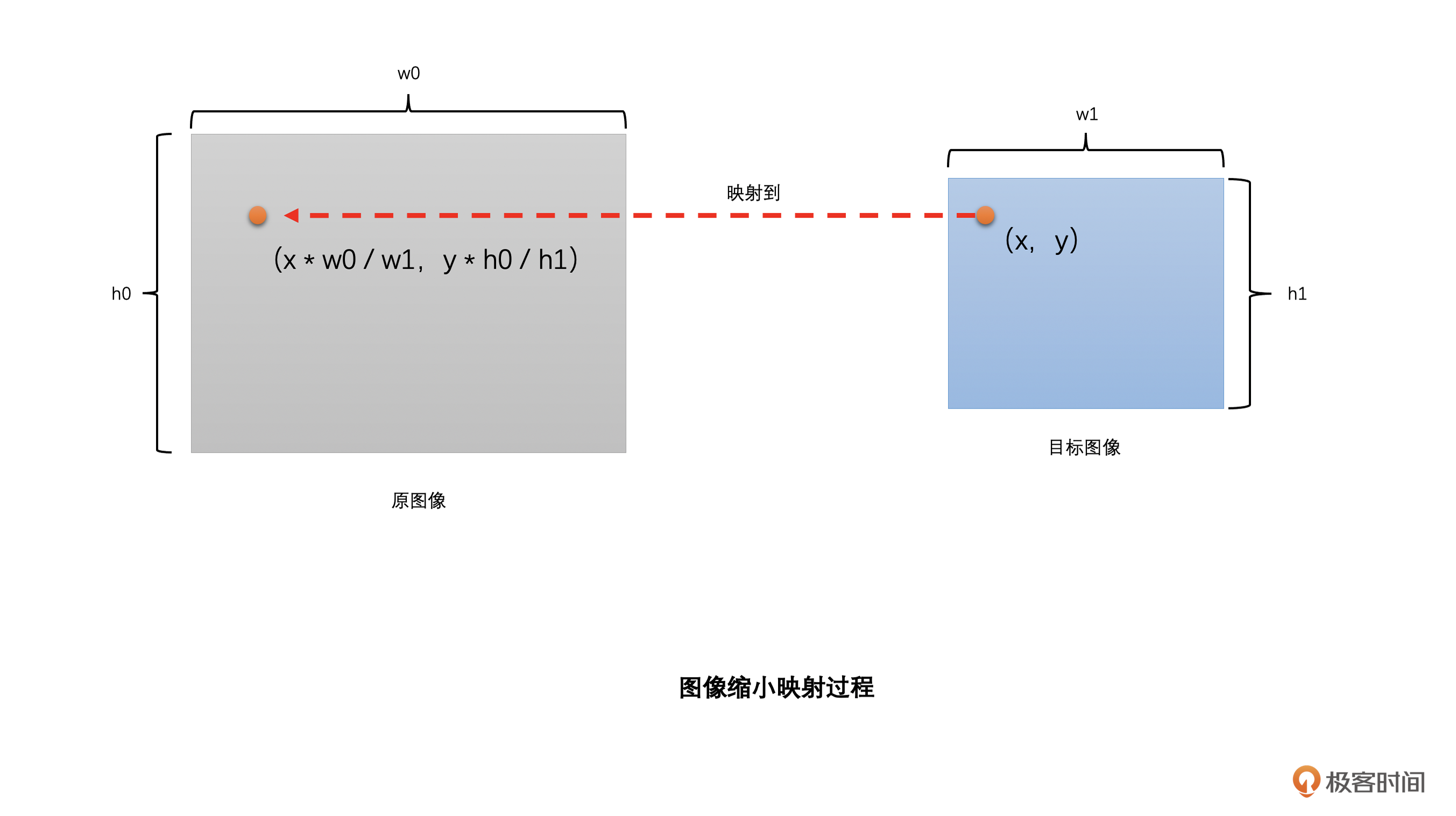
|
|||
|
|
|
|||
|
|
## 三种插值算法
|
|||
|
|
|
|||
|
|
到这里我们已经讲完了图像缩放的基本原理,我们注意到,位置映射过程很简单,主要的工作就是如何通过插值算法得到原图像映射位置的像素值。同时,需要说明一下,图像缩放和插值在RGB和YUV颜色空间中都可以进行。因此,我们下面不会对颜色空间做区分。接下来,我们就依次介绍一下三种插值算法,看看它们的具体插值原理是怎样的,以及它们的效果又是怎样的。
|
|||
|
|
|
|||
|
|
### 最近邻插值
|
|||
|
|
|
|||
|
|
我们先来聊聊最简单的**最近邻插值算法**。顾名思义,最近邻插值就是:
|
|||
|
|
|
|||
|
|
* 首先,将目标图像中的目标像素位置,映射到原图像的映射位置。
|
|||
|
|
* 然后,找到原图像中映射位置周围的4个像素。
|
|||
|
|
* 最后,取离映射位置最近的像素点的像素值作为目标像素。
|
|||
|
|
|
|||
|
|
比如说,我们现在要将图像从720P放大到1080P。下面我们给出1080P目标图像中3个像素点(0,0)、(1,0)和(2,2)的最近邻插值过程。
|
|||
|
|
|
|||
|
|
1. 1080P图像的(0,0)位置的像素,我们映射到720P图像的映射位置就是(0 \* 1280 / 1920,0 \* 720 / 1080),也就是(0,0)位置,那1080P的(0,0)位置的像素值直接取原图像(0,0)像素点的像素值就可以了。
|
|||
|
|
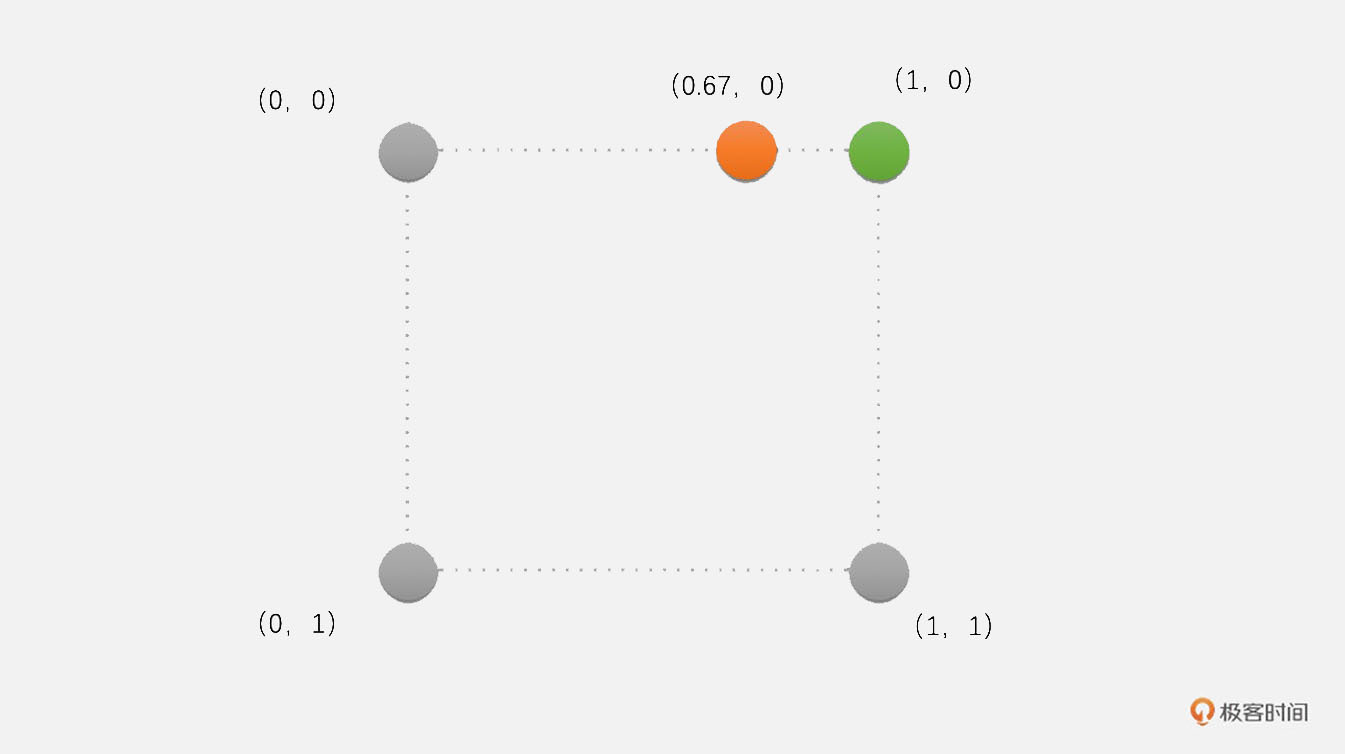
2. 对于1080P图像的(1,0)位置的像素,我们映射到720P图像就是(1 \* 1280 / 1920, 0 \* 720 / 1080),也就是(0.67,0)位置的像素,这个像素需要插值得到。使用最近邻插值的话,(0.67,0)周围的4个像素分别是(0,0)、(1,0)、(0,1)和(1,1),其中距离(0.67,0)最近的位置很明显是(1,0)位置的像素。因此,我们将原图像中(1,0)位置的像素值赋值给目标图像(1,0)位置的像素点。
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
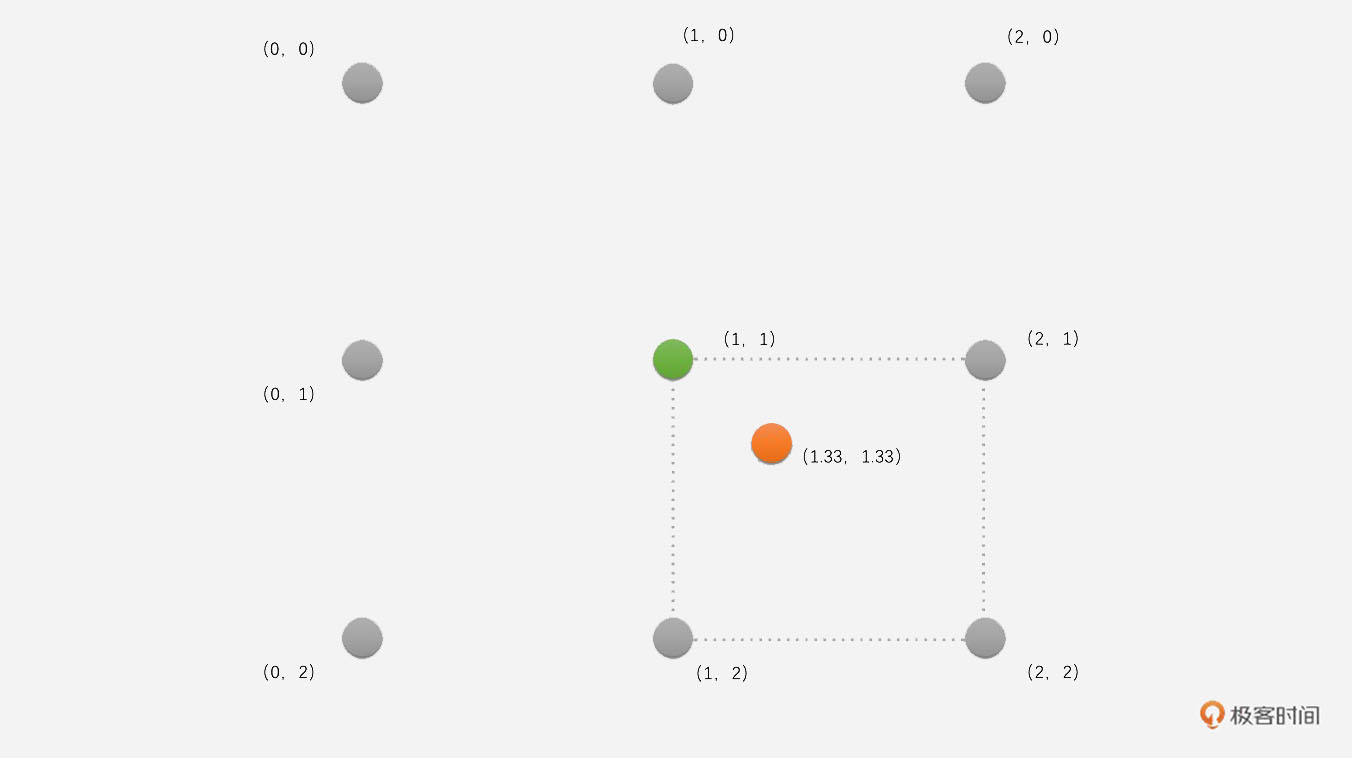
3. 对于1080P图像的(2,2)位置呢?同样映射到720P图像,映射位置是(2 \* 1280 / 1920,2 \* 720 / 1080),也就是(1.33,1.33)位置,其周围4个像素分别是(1,1)、(1,2)、(2,1)和(2,2),很明显(1,1)离(1.33,1.33)位置最近,那我们取原图像(1,1)的像素值赋值给1080P图像的(2,2)位置的像素点。
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
照着这个步骤一个个像素插值下去就可以得到1080P的图像了。是不是很简单?这个过程就是通过目标图像的像素位置,按照缩放比例映射到原图像,然后找到原图像中离映射位置最近的像素点,把它的像素值赋值给目标图像的像素就可以了。
|
|||
|
|
|
|||
|
|
最近邻插值有一个明显的**缺点**,就是**它直接使用离插值位置最近的整数位置的像素作为插值像素,这样会导致相邻两个插值像素有很大的概率是相同的**。比如说,上面例子中的(1,0)位置和(2,0)位置的像素值是一样的。这样**得到的放大图像大概率会出现块状效应,****而****缩小图像容易出现锯齿**。这是最近邻插值的缺点。但是它也有一个优点,就是**不需要太多的计算,速度非常的快**。
|
|||
|
|
|
|||
|
|
### 双线性插值
|
|||
|
|
|
|||
|
|
介绍完了最近邻插值算法,接下来我们将要介绍双线性插值算法。
|
|||
|
|
|
|||
|
|
双线性插值相比于最近邻插值稍微复杂一些,它也是取待插值像素周围的4个像素,不同的是,它需要**将这4个像素值通过一定的运算得到最后的插值像素**。在开始讲双线性插值的原理之前,我们先来看看双线性插值的基础,也就是线性插值的原理。
|
|||
|
|
|
|||
|
|
线性插值是在两个点中间的某一个位置插值得到一个新的值。线性插值认为,这个需要插值得到的点跟这两个已知点都有一定的关系,并且,待插值点与离它近的那个点更相似。因此,**线性插值是一种以距离作为权重的插值方式,距离越近权重越大,距离越远权重越小**。
|
|||
|
|
|
|||
|
|
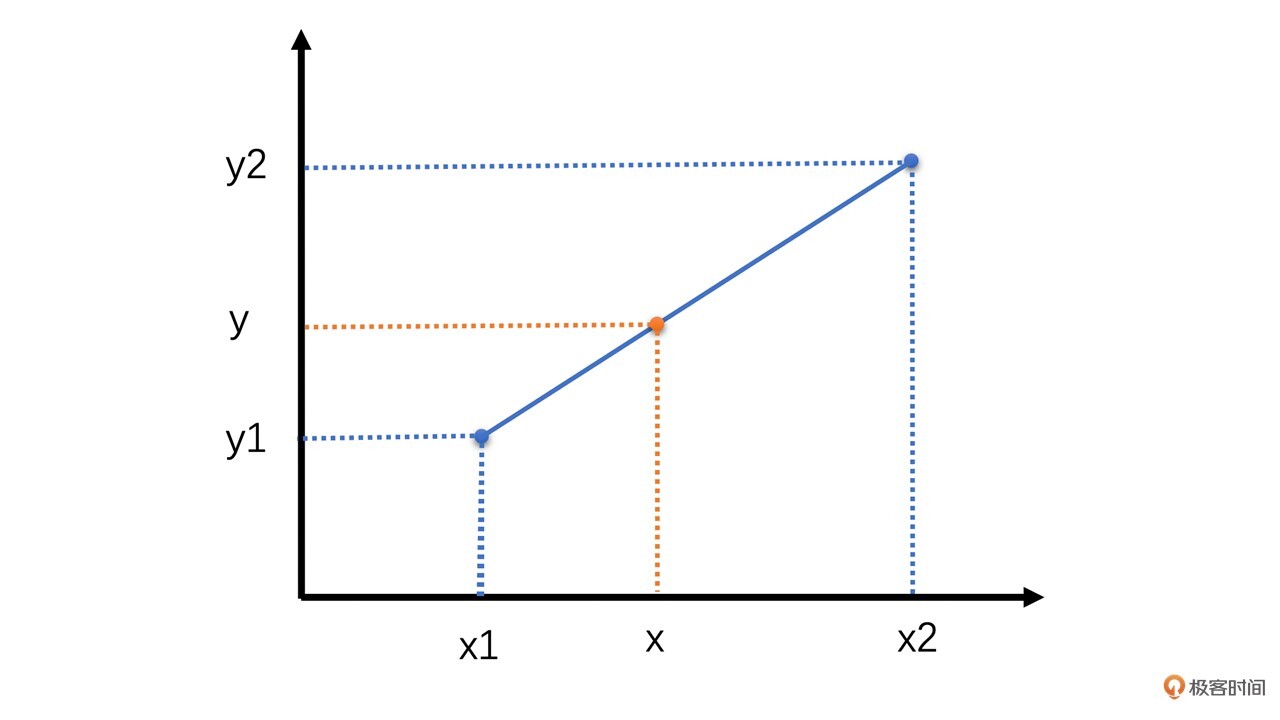
比如,如下图所示,已知 (x1,y1) 与 (x2,y2)两个点,需求得x对应的y值。
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
通过线性插值方法,y值的计算公式如下:
|
|||
|
|
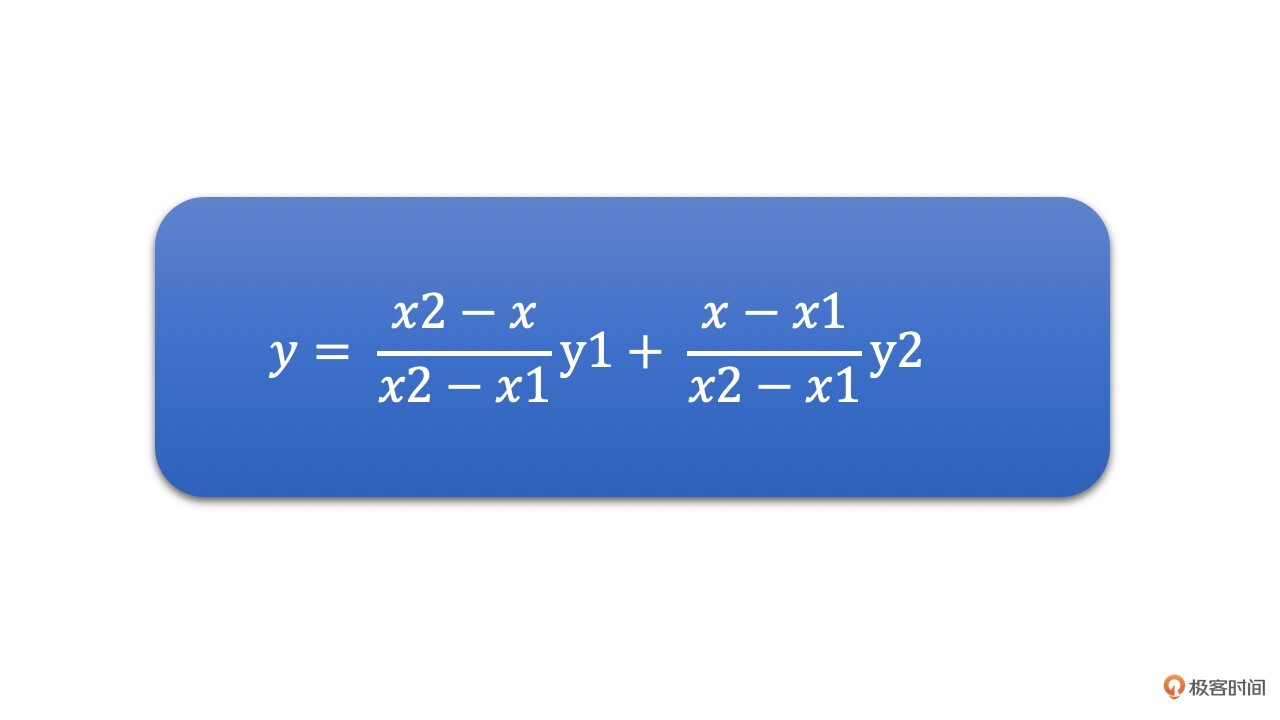
|
|||
|
|
|
|||
|
|
**双线性插值本质上就是在两个方向上做线性插值**。由于图像是两个方向的二维数据,正好适合使用双线性插值算法。下面我们来讲讲双线性插值的具体原理。
|
|||
|
|
|
|||
|
|
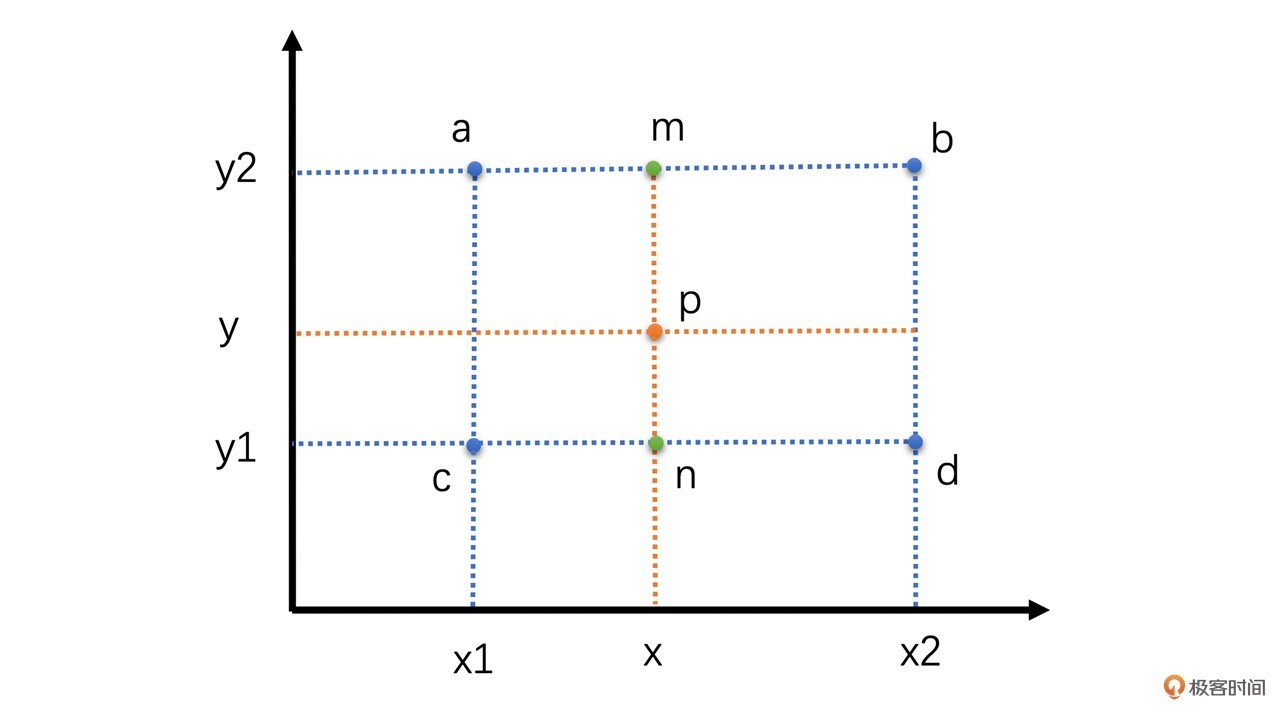
**双线性插值其实就是三次线性插值的过程**,我们先通过两次线性插值得到两个中间值,然后再通过对这两个中间值进行一次插值得到最终的结果。如下图所示:
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
假设我们要插值求的点是p点,其坐标为(x,y)。已知周围4个像素分别是a、b、c、d。我们先通过a和b水平线性插值求得m,再通过c、d水平插值求得n。有了m和n之后,再通过m、n垂直插值求得p点的像素值。计算过程如下:
|
|||
|
|
|
|||
|
|

|
|||
|
|
|
|||
|
|
我们还是以720P放大到1080P为例,那么1080P图像中的目标像素点(2,2)的双线性插值过程是怎么样的呢?
|
|||
|
|
|
|||
|
|
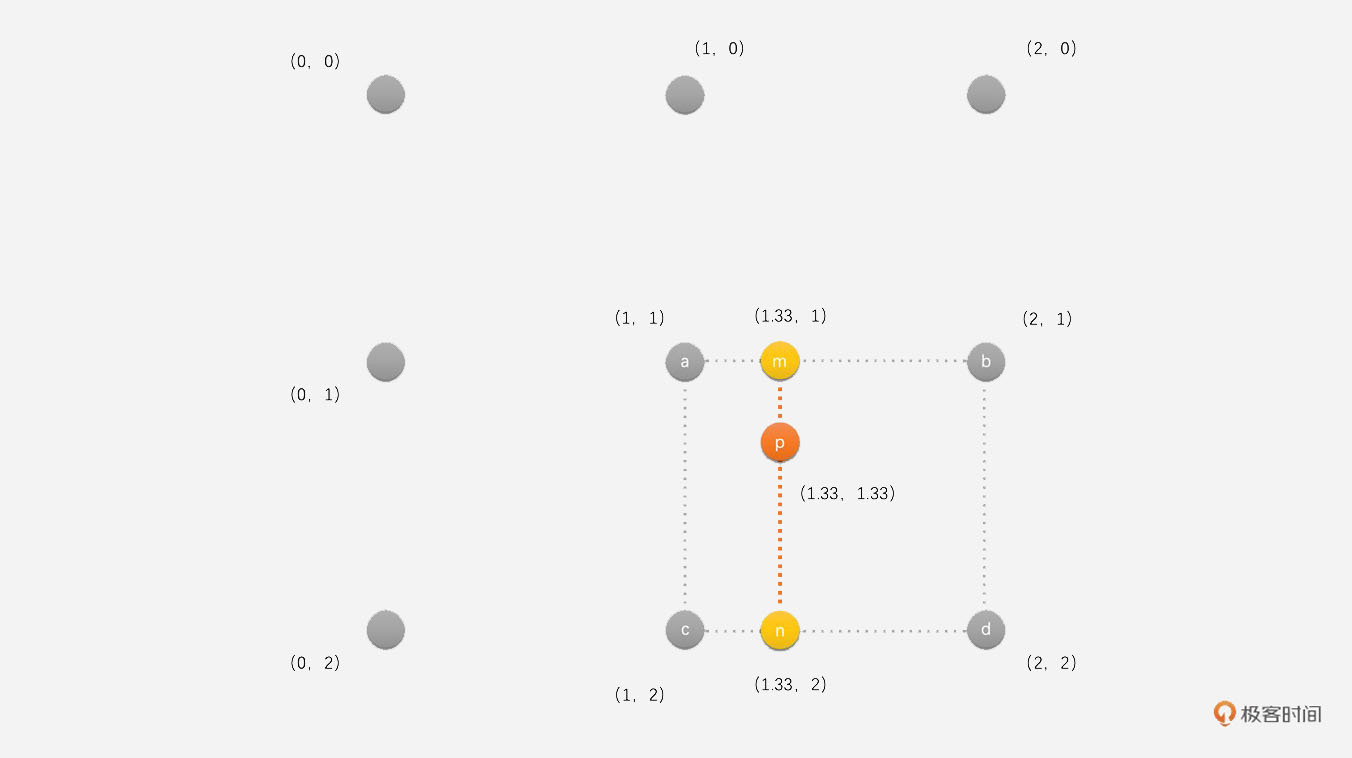
首先,将目标像素点(2,2)映射到原图像的(1.33,1.33)位置,对应下面图中的点p。找到(1.33,1.33)周围的4个像素(1,1)、(2,1)、(1,2)和(2,2),分别对应图中的点a、b、c和d。
|
|||
|
|
|
|||
|
|
|
|||
|
|
先通过这4个像素插值得到中间像素m和n的像素值。m和n的坐标分别为(1.33,1)和(1.33,2)。通过上面的公式可以求得点p(1.33,1.33)的像素值是:
|
|||
|
|
|
|||
|
|

|
|||
|
|
|
|||
|
|
插值求得(1.33,1.33)的值之后,将其赋值给1080P目标图像的(2,2)位置的像素点就可以了。这就是双线性插值的过程。
|
|||
|
|
|
|||
|
|
**双线性插值相比最近邻插值运算要多一些**,因此运行时间要长一些,但是相比而言,**插值之后图像效果会好于最近邻插值**。
|
|||
|
|
|
|||
|
|
### 双三次插值
|
|||
|
|
|
|||
|
|
下面我们接着来看一种效果相比双线性插值更好一些的插值算法,就是双三次插值算法,也叫BiCubic插值。
|
|||
|
|
|
|||
|
|
在最近邻插值算法中,我们选择待插值像素周围的4个像素,并取离待插值像素位置最近的像素点权重为1,其余3个点权重为0。在双线性插值算法中,同样选择待插值像素周围的4个像素,并且每个像素以距离作为权重,距离越近权重越大,距离越远权重越小。
|
|||
|
|
|
|||
|
|
双三次插值算法的基本原理同前两种插值算法差不多,不同的是:
|
|||
|
|
|
|||
|
|
第一,**双三次插值选取的是周围的16个像素**,比前两种插值算法多了3倍。
|
|||
|
|
|
|||
|
|
第二,双三次插值算法的**周围像素的权重计算是使用一个特殊的BiCubic基函数来计算的**。
|
|||
|
|
|
|||
|
|
我们先通过这个BiCubic基函数计算得到待插值像素周围16个像素的权重,然后将16个像素加权平均就可以得到最终的待插值像素了。
|
|||
|
|
|
|||
|
|

|
|||
|
|
BiCubic基函数形式如下:
|
|||
|
|

|
|||
|
|
|
|||
|
|
**双三次插值的权重值是分水平和垂直两个方向分别求得的,计算公式是一样的,都是上面这个公式**。对于周围16个点中的每一个点,其坐标值为(x,y),而目标图像中的目标像素在原图像中的映射坐标为p(u,v)。那么通过上面公式可以求得其水平权重W(u - x),垂直权重W(v - y)。将W(u - x)乘以W(v - y)得到最终权重值,然后再用最终权重值乘以该点的像素值,并对16个点分别做同样的操作并求和,就得到待插值的像素值了。公式如下:
|
|||
|
|

|
|||
|
|
|
|||
|
|
我们还是以720P放大到1080P为例,那么1080P图像中的目标像素点(2,2)的双三次插值过程是怎么样的呢?
|
|||
|
|
|
|||
|
|
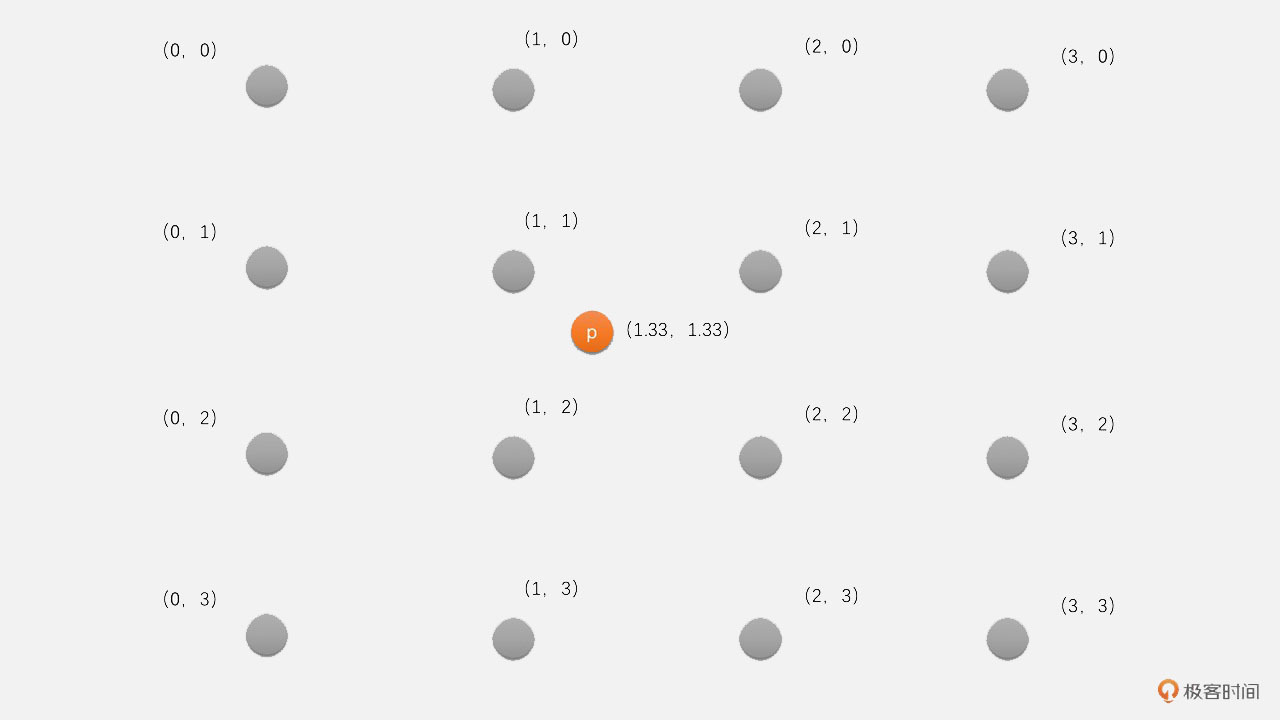
首先,将目标像素点(2,2)映射到原图像的(1.33,1.33)位置,对应下面图中的点p。找到(1.33,1.33)周围的16个像素(0,0)、(1,0)一直到(3,3)。
|
|||
|
|
|
|||
|
|
|
|||
|
|
然后,通过BiCubic函数求得每一个点的水平和垂直权重。例如,(0,0)、(1,2)和(3,3)点的水平权重和垂直权重计算方式如下:
|
|||
|
|
|
|||
|
|

|
|||
|
|
|
|||
|
|
求出这16个点的水平和垂直权重,两者相乘得到最终的权重值,之后每一个像素用自己的最终权重乘以自己的像素值再求和就是(1.33,1.33)的插值像素值了。将它赋值给1080P图像的(2,2)像素点就可以了。
|
|||
|
|
|
|||
|
|
我们可以看到,**双三次插值需要计算16个点的权重再乘以像素值求和,相较于前面的最近邻插值和双线性插值计算量较大,但插值后的图像效果最好**。
|
|||
|
|
|
|||
|
|
好了,我们通过下面几幅图像来对比一下这三种插值算法的效果。我们可以看到:最近邻插值得到的图像有很多块效应,效果最差;双线性插值稍好于最近邻插值一些,但是比较模糊;双三次插值效果最好,对比度也明显好于双线性插值。
|
|||
|
|
|
|||
|
|

|
|||
|
|
|
|||
|
|
## 小结
|
|||
|
|
|
|||
|
|
好了,这节课到这里就要结束了。我们来回顾一下今天的学习内容。
|
|||
|
|
|
|||
|
|
我们主要讨论了图像的缩放算法。图像缩放主要包括两个部分:一个是像素位置映射过程;一个是映射位置像素的插值过程。
|
|||
|
|
|
|||
|
|
1. 像素位置映射过程
|
|||
|
|
|
|||
|
|
对于分辨率为w0 x h0的原图像,我们需要缩放到分辨率为w1 x h1的目标图像。我们只需要将目标图像的每一个像素点(x,y)映射到原图像的(x \* w0 / w1,y \* h0 / h1)位置。一般这个映射位置不是一个整数位置。我们需要通过插值算法得到映射位置的像素值,然后将映射位置插值得到的像素值赋值给目标像素就可以了。
|
|||
|
|
|
|||
|
|
2. 映射像素的插值过程
|
|||
|
|
|
|||
|
|
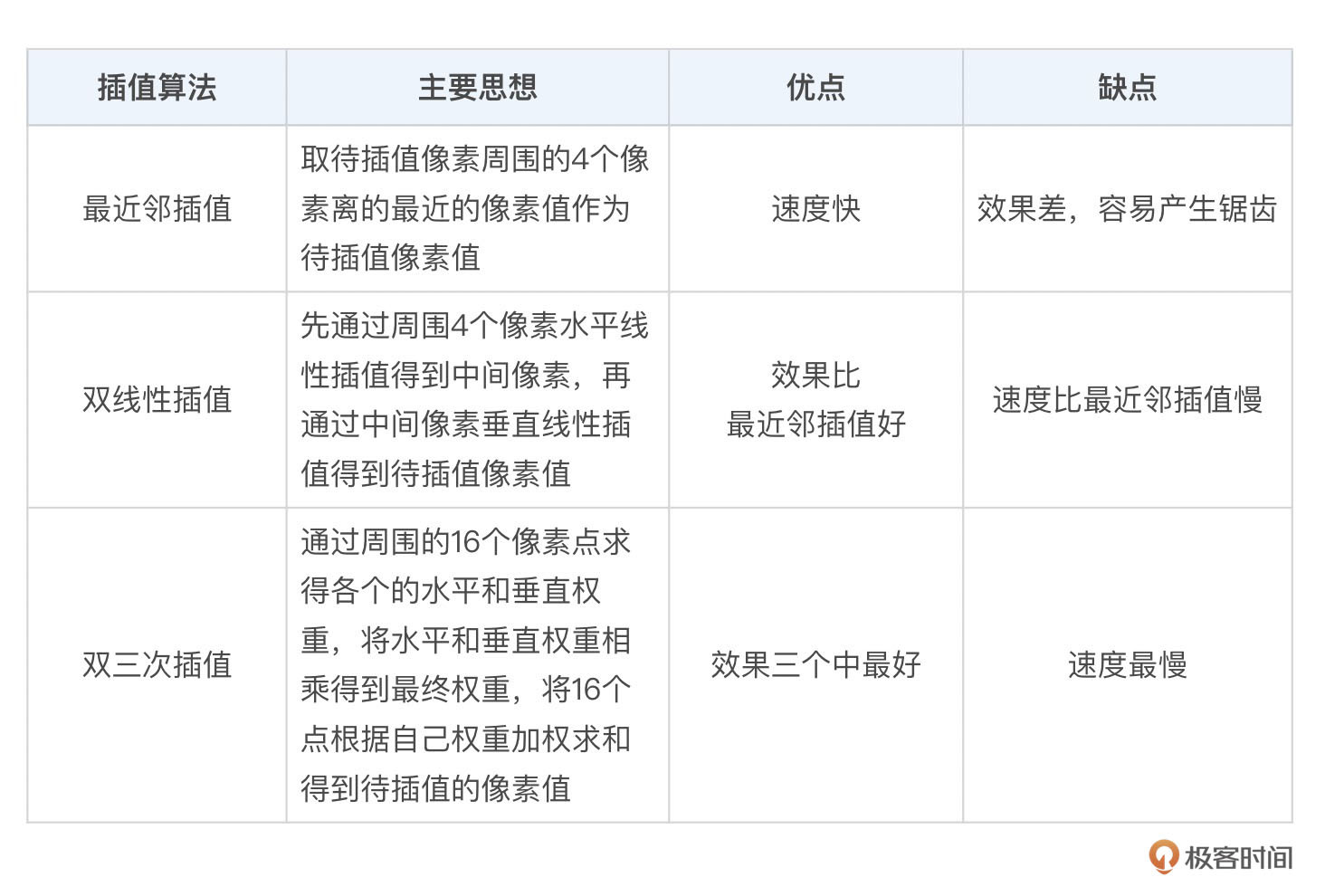
插值过程主要会使用到插值算法。我们今天介绍了最常用的三种插值算法,分别是最近邻插值、双线性插值和双三次插值算法。三种算法的思想和优缺点如下表所示。
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
## 思考题
|
|||
|
|
|
|||
|
|
现在我有一个思考题留给你。
|
|||
|
|
|
|||
|
|
双三次插值需要周围16个像素,对于左上角的点,比如(0.5,0.5),它周围不够16个点怎么办呢?
|
|||
|
|
|
|||
|
|
欢迎你在留言区和我分享你的思考和疑惑,你也可以把今天所学分享给身边的朋友,邀请他加入探讨,共同进步。下节课再见。
|
|||
|
|
|