426 lines
24 KiB
Markdown
426 lines
24 KiB
Markdown
|
|
# 12|拓扑排序:Webpack是如何确定构建顺序的?
|
|||
|
|
|
|||
|
|
你好,我是微扰君。
|
|||
|
|
|
|||
|
|
Webpack是现在最流行的前端构建工具,见证了前端工程化在过去十年里的繁荣发展。如果你是前端工程师,相信你在日常工作中应该会经常使用到。
|
|||
|
|
|
|||
|
|
Webpack让我们可以模块化地进行现代Web应用的前端开发,并基于我们的简单配置,从入口开始,递归地自动构建出复杂的依赖关系图,最终把所有的模块打包成若干个浏览器可理解的bundle。
|
|||
|
|
|
|||
|
|
整个过程比较复杂,但是其中显然会有一个构建顺序的问题需要处理。以 `html-webpack-plugin v3.2.0` 为例,我们用Webpack打包HTML文件的时候,文件之间会有一定的引用依赖关系,因而所构建的chunk之间也会有相应的依赖关系。
|
|||
|
|
|
|||
|
|
那问题就来了,打包的时候,**按照什么样的顺序去打包才更合理呢?这就是拓扑排序需要解决**。
|
|||
|
|
|
|||
|
|
我的第一份工作就是前端工程师,对前端开发感情挺深,也一直觉得其实前端里用到算法的地方绝对不在少数。所以今天我们就以Webpack为例,一起来学习拓扑排序在实战中所发挥的威力。
|
|||
|
|
|
|||
|
|
当然,如果你对Webpack了解不多,也不用担心,完全可以把这个问题看成如何在一堆有依赖关系的源文件中找到合适的加载或者编译的顺序,和你常用的maven、makefile这类编译和依赖管理工具,去编译项目的原理并无二致。
|
|||
|
|
|
|||
|
|
好,我们马上开始今天的学习,首先我们得来讲解一下拓扑排序的依据——拓扑序是什么。
|
|||
|
|
|
|||
|
|
## 拓扑排序
|
|||
|
|
|
|||
|
|
“拓扑”序,光听名字你是不是感觉很抽象不好懂,我们看一个生活中的例子。
|
|||
|
|
|
|||
|
|
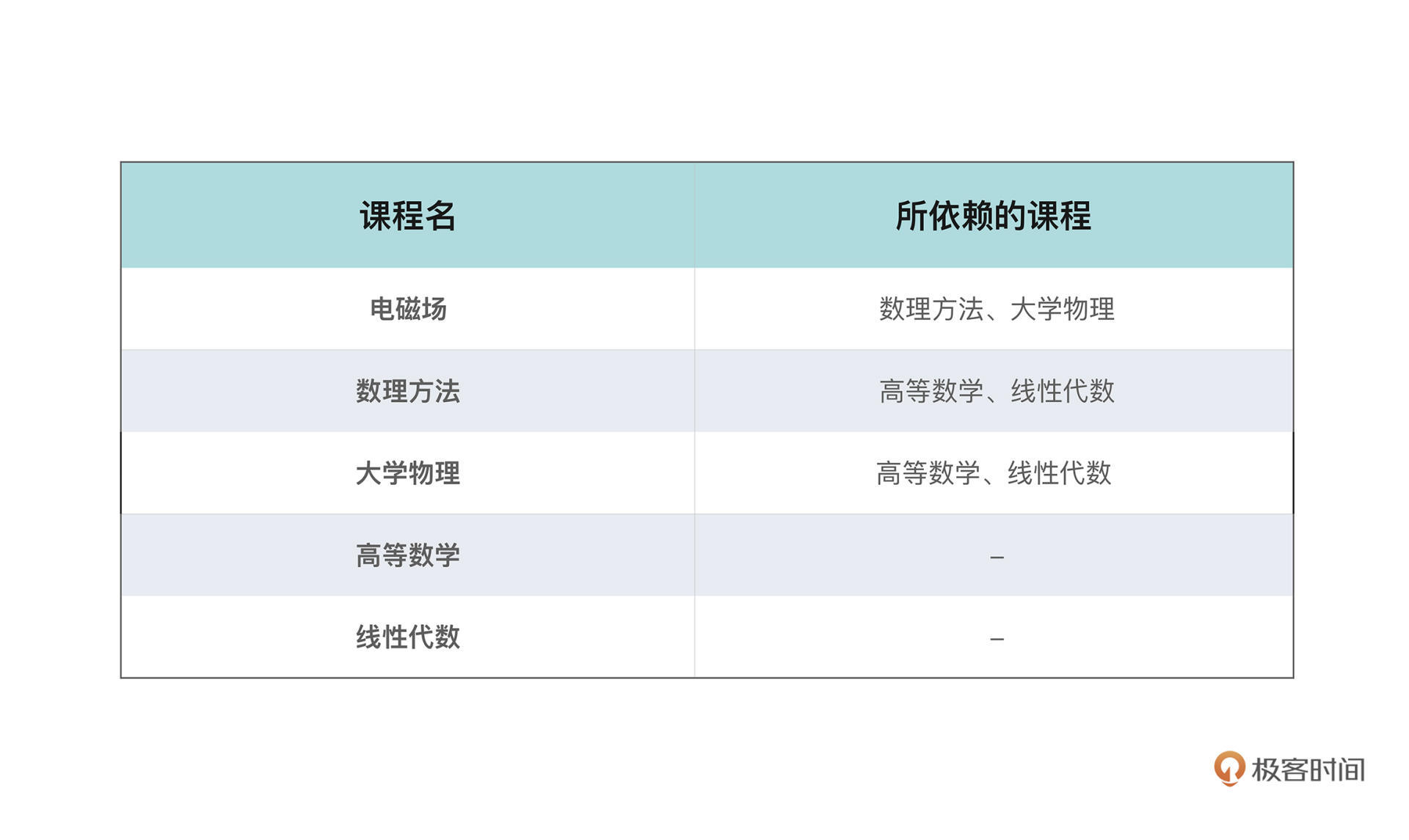
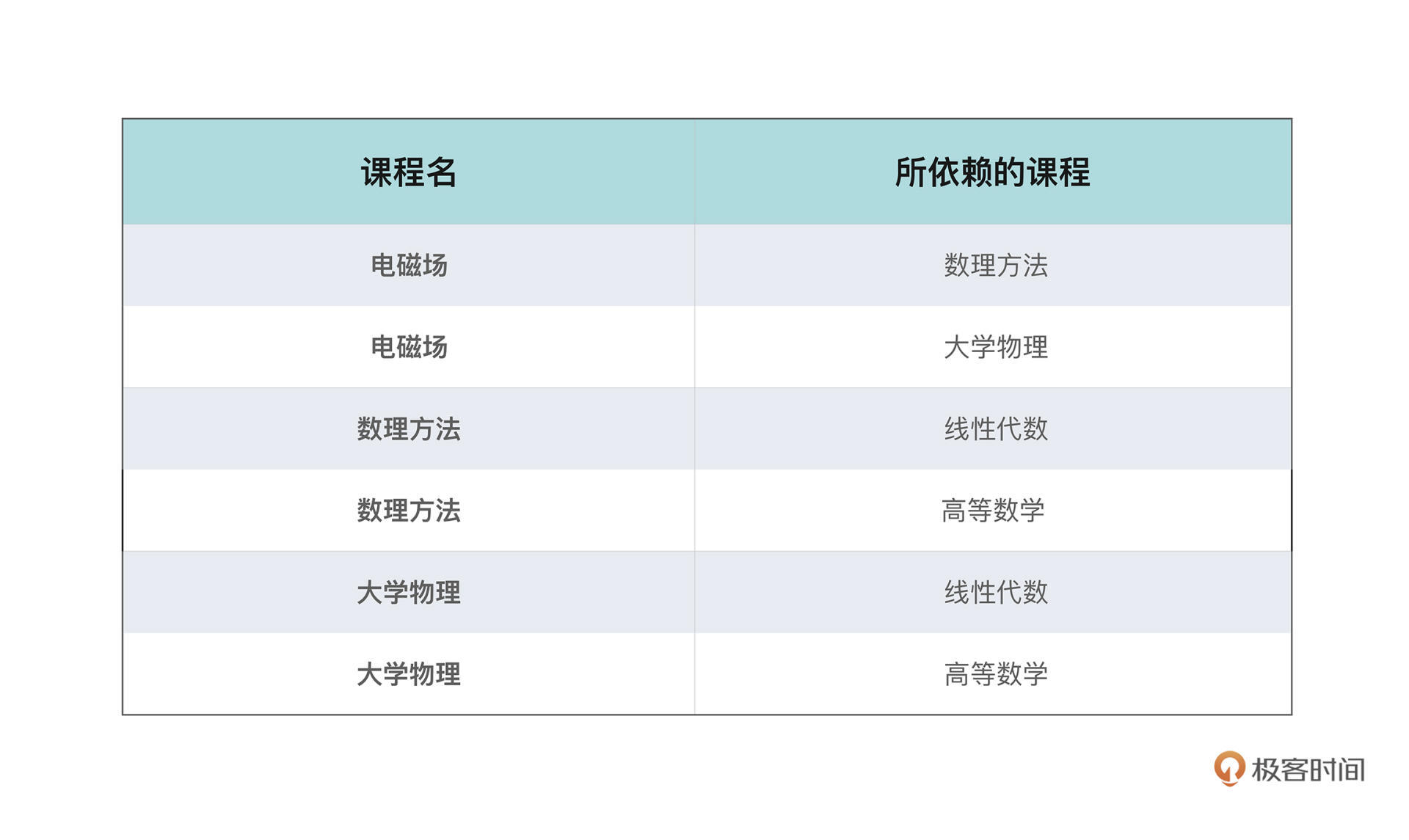
在大学,学生往往有更大的选课自由,可以按照自己的兴趣选择不同的课程、在不同的时间修读。但是,显然许多课程,和代码之间的依赖一样,也有着修读顺序的先后要求;有些课程还可能有不止一门先修课程,比如电磁场就要求先修读大学物理和数理方法两门课。
|
|||
|
|
|
|||
|
|
所以请问如果给了你一张这样的必修课表,每一行包含了课程本身的信息和它所依赖的其他课,你应该怎么安排你的课程学习顺序呢?这也是力扣上出镜率非常高的一道面试题[课程表](https://leetcode-cn.com/problems/course-schedule)。
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
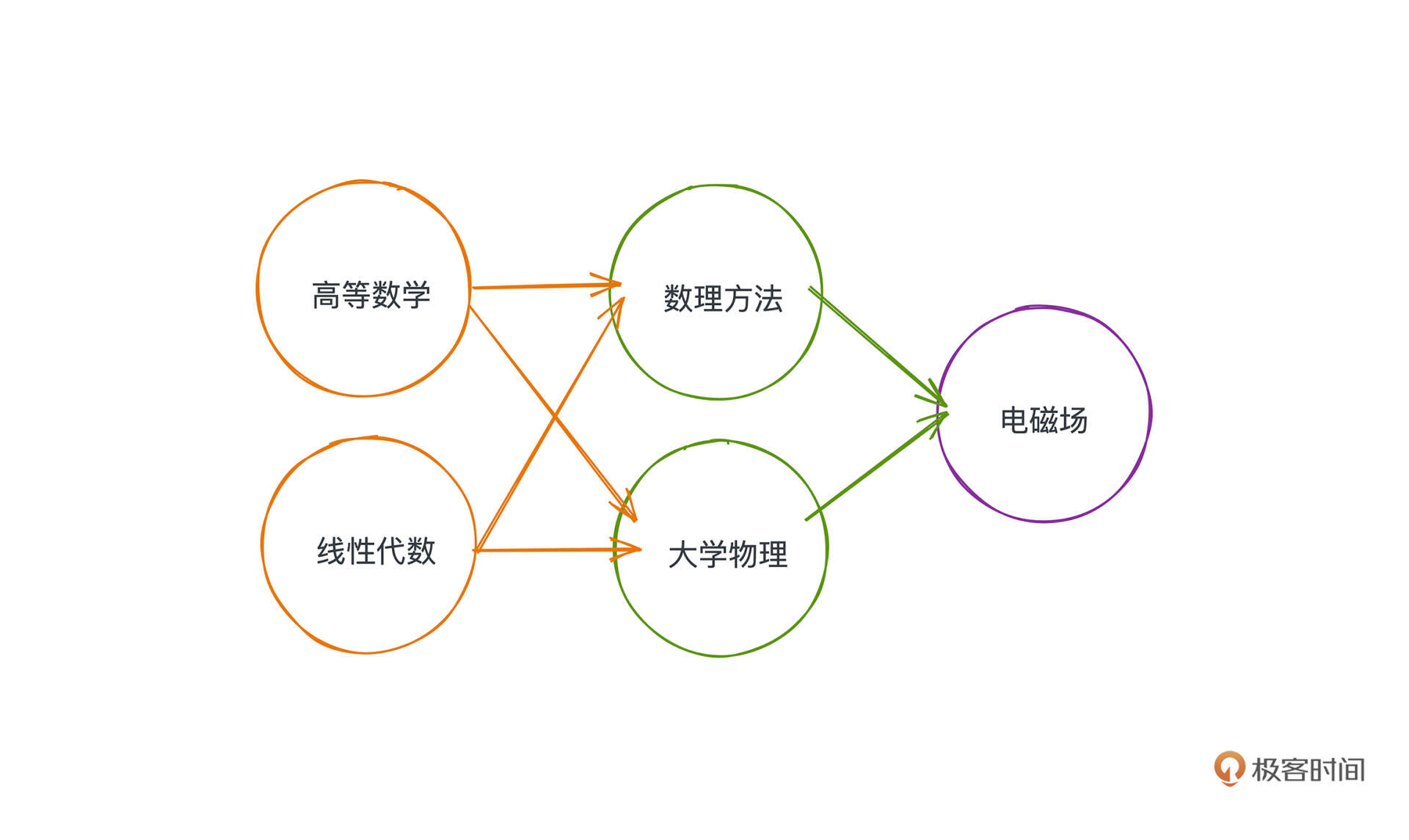
看表格不太清晰,这些课程之间的修读关系,**显然可以用有向图来抽象,节点就是课程本身,边代表了两门课程的依赖关系**。把课程表的信息用图的方式表示出来就会是这个样子:
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
照着图去选择修读顺序就会容易很多,你会优先选择没有入边也就是没有先修要求的课程,所以,等修读完线性代数和高等数学之后你就会发现,诶这个时候数理方法和大学物理的先修课程已经全部被你解锁了;继而你就可以继续修读这两门课程;最后再修读电磁场这门。
|
|||
|
|
|
|||
|
|
当然你会发现修读顺序依旧不只一种,比如:
|
|||
|
|
|
|||
|
|
```python
|
|||
|
|
线性代数、高等数学、数理方法、大学物理、电磁场
|
|||
|
|
高等数学、线性代数、大学物理、数理方法、电磁场
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
这两种修读顺序的都是合理的,但它们一定保证了,要修读的课程的先修课程一定在当前课程的前面。
|
|||
|
|
|
|||
|
|
讲到这里,拓扑序的概念就清晰了,我们给出一个序列使得**每个节点只出现一次,且保证如果存在路径P从A指向B,那么A在序列中一定出现在B之前;满足这个条件的序列就被称为满足拓扑序**,所以它常常被用来解决有依赖关系任务的排序问题。
|
|||
|
|
|
|||
|
|
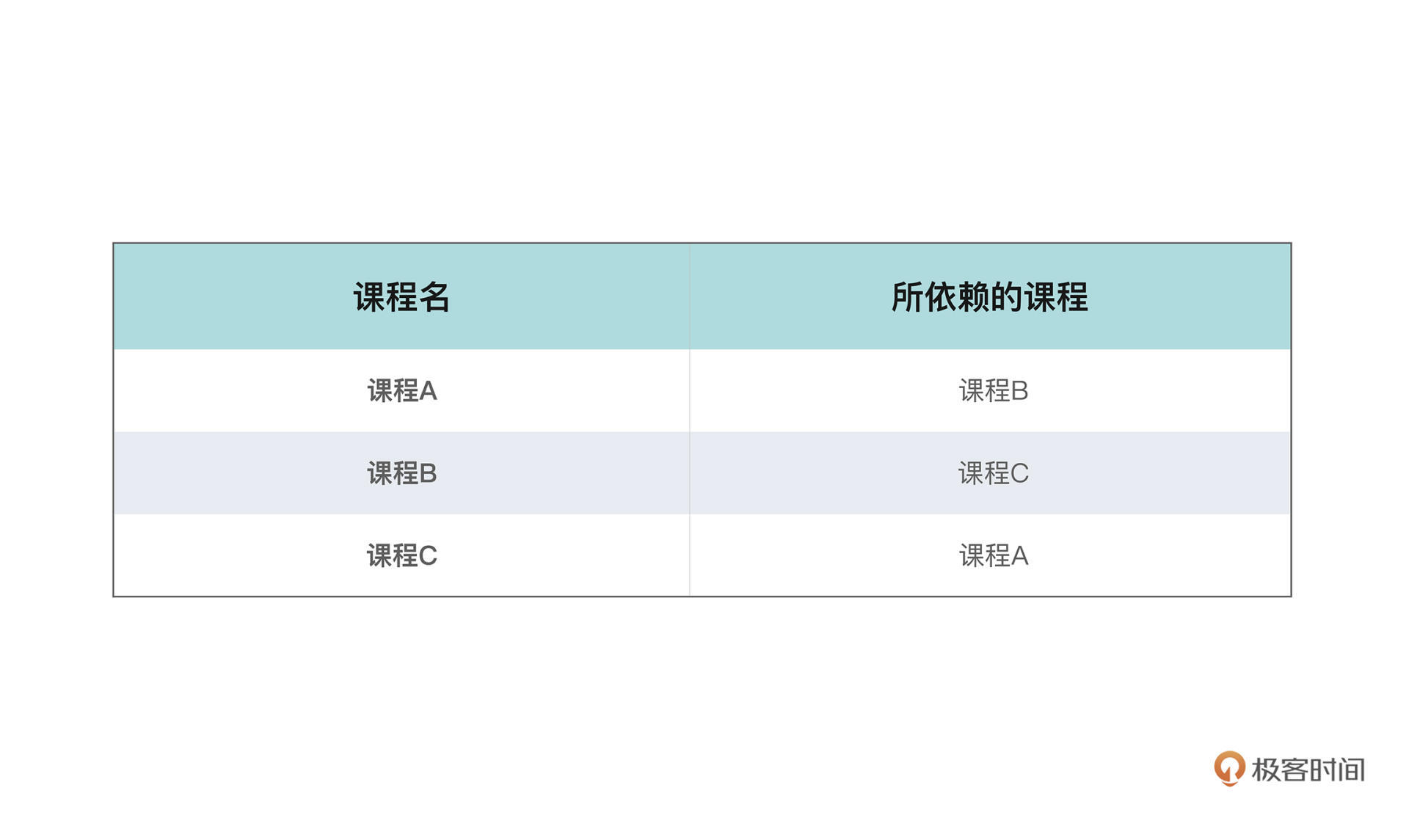
对于一个有向图而言,通常存在不止一种拓扑排序的方式。那有没有什么样的图是不能被拓扑排序的呢?当然是有的。假设有这样一张课表:
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
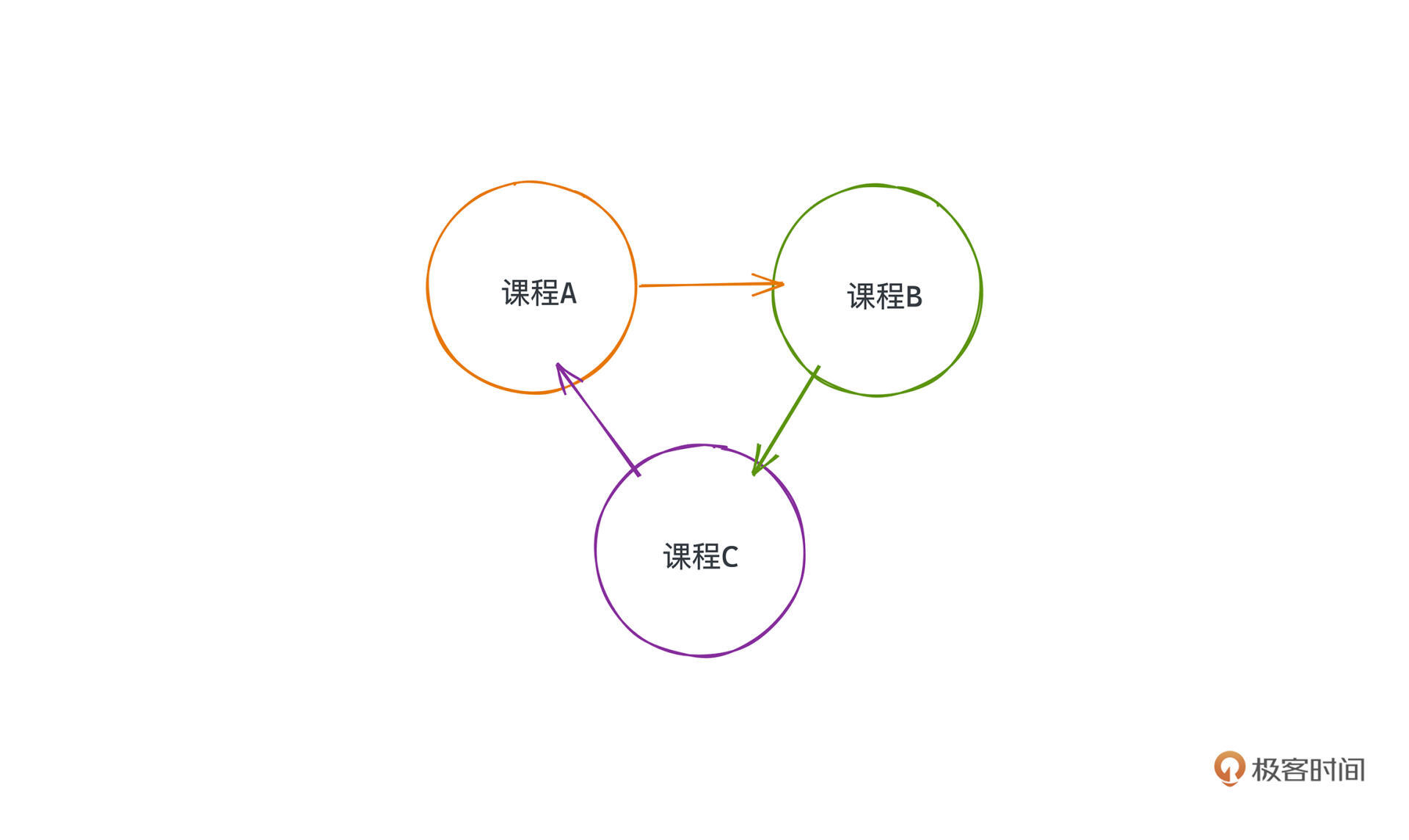
乍一看,可能和其他课表也没什么区别,但如果你把依赖关系同样表示在图上就会发现一些问题了。
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
它们之间构成了循环依赖的关系,你无法找到第一门修读的课程,所以这种先修课程的安排关系在现实世界中也是不存在的,这样的情况其实和我们常说的死锁有点像。你永远没有办法在一个有向有环的图中找到可以被拓扑排序的方案。
|
|||
|
|
|
|||
|
|
所以,**所有拓扑排序都是建立在有向无环图(DAG)上的**,DAG这个词相信很多同学都很眼熟,在Flink和Spark这类可以用来做数据批计算或者流计算的框架中,就常常可以见到DAG这样的概念,用来做计算任务的调度。
|
|||
|
|
|
|||
|
|
好,现在我们已经知道拓扑排序是什么了,也知道它可以用来解决有依赖关系任务的排序问题。那拓扑排序的具体实现步骤到底是什么样的呢?
|
|||
|
|
|
|||
|
|
## 拓扑排序如何实现
|
|||
|
|
|
|||
|
|
有两种经典的算法可以实现,一种叫Khan算法,基于贪心和广度优先算法BFS的思想来解决这个问题,另一种则是基于深度优先算法DFS的思想(如果你对DFS和BFS的概念还不够熟悉,可以再复习一下之前的[章节](https://time.geekbang.org/column/article/474363))。
|
|||
|
|
|
|||
|
|
### khan算法
|
|||
|
|
|
|||
|
|
Khan算法是更符合我们直觉的一种方法,也更容易理解,我们就先来讲解基于BFS的Khan算法如何解决课程表问题,也就是LeetCode 210,感兴趣的话你可以课后可以去网站上提交一下这道题。
|
|||
|
|
|
|||
|
|
题目是这样的:假设你总共有 numCourses 门课需要选,记为从 0 到 numCourses - 1,给你一个数组 prerequisites 存储课程之间的依赖关系,其中 prerequisites\[i\] = \[ai, bi\] ,表示在选修课程 ai 前必须先选修 bi 。
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
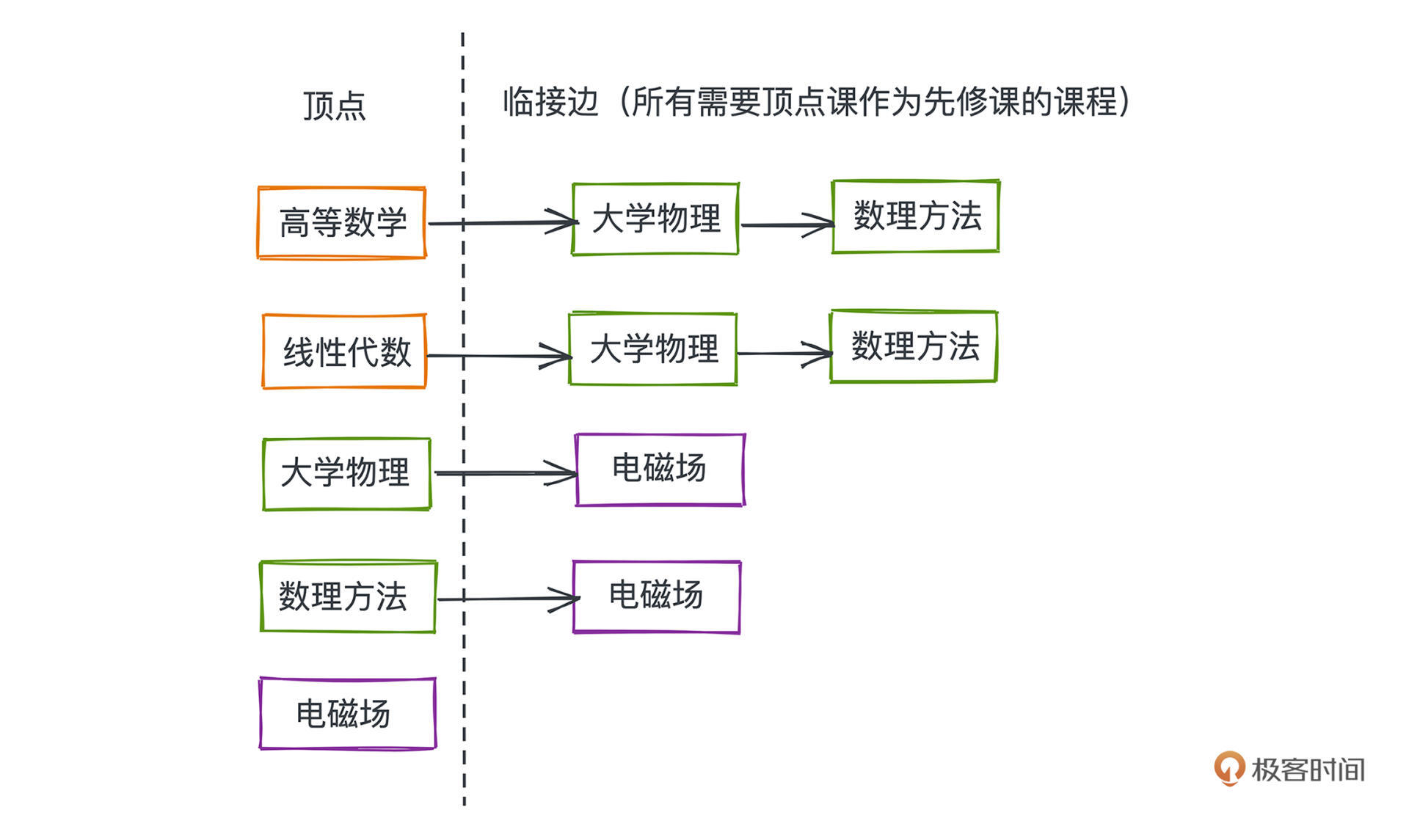
可以看到,输入的是课程间两两的依赖关系,事实上,**这也是一种图的存储方式,prerequisites就是图上所有边的集合,我们一般称为边表**。但是边表的存图方式不能让我们快速找到某个节点的后继节点,所以我们需要一种新的表示方式。
|
|||
|
|
|
|||
|
|
因为每个课程都是用 0 到 numCourses - 1 的数字作为课程标识,我们可以直接用一个二维数组next来表示图,next\[i\]里存储的是所有需要i作为先修课程的课程。这也是一种图的表示方法,我们一般叫做**邻接表**,通常可以用HashMap、数组、链表等数据结构实现。
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
相比于邻接矩阵存储所有节点之间是否存在边,在邻接表中,我们只用存储实际存在的边,所以在稀疏图中比较节约空间,实际应用和算法面试中都非常常见。
|
|||
|
|
|
|||
|
|
```python
|
|||
|
|
vector<vector<int>> next(numCourses, vector<int>());
|
|||
|
|
for (auto edge: prerequisites) {
|
|||
|
|
int n = edge[0];
|
|||
|
|
int p = edge[1];
|
|||
|
|
|
|||
|
|
next[p].push_back(n);
|
|||
|
|
}
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
为了构建这样一张邻接表,我们要做的事就是遍历所有的先修关系,把edge\[0\]推入edge\[1\]所对应的课程列表也就是邻接表数组中。
|
|||
|
|
|
|||
|
|
输入处理完成,所有课程的先修关系图我们就有了。下一步就是选择合适的修读顺序。
|
|||
|
|
|
|||
|
|
相信你很自然就会想到,诶,那我们**把所有不用先修课程的课都修完,然后从剩下的课程里找出接下来可修读的课程**是不是就行了?之后按这样的顺序反复进行,直到所有课程都修读完毕。其实基于贪心思想的Khan算法就是这样做的。而这样一轮一轮遍历的感觉是不是也让你想到之前讲过的地毯式搜索的BFS呢?
|
|||
|
|
|
|||
|
|
我们一起来看整个题目Khan算法的实现:
|
|||
|
|
|
|||
|
|
```python
|
|||
|
|
class Solution {
|
|||
|
|
public:
|
|||
|
|
vector<int> findOrder(int numCourses, vector<vector<int>>& prerequisites) {
|
|||
|
|
// 邻接表数组
|
|||
|
|
vector<vector<int>> next(numCourses, vector<int>());
|
|||
|
|
// 入度表
|
|||
|
|
vector<int> pre(numCourses, 0);
|
|||
|
|
// 标记是否遍历过
|
|||
|
|
vector<int> visited(numCourses, 0);
|
|||
|
|
// 记录最终修读顺序
|
|||
|
|
vector<int> ans;
|
|||
|
|
|
|||
|
|
// 构图
|
|||
|
|
for (auto edge: prerequisites) {
|
|||
|
|
int n = edge[0];
|
|||
|
|
int p = edge[1];
|
|||
|
|
|
|||
|
|
next[p].push_back(n);
|
|||
|
|
pre[n]++;
|
|||
|
|
}
|
|||
|
|
|
|||
|
|
queue<int> q;
|
|||
|
|
|
|||
|
|
// 所有没有先修课程的课程入队
|
|||
|
|
for (int i = 0; i < numCourses; i++) {
|
|||
|
|
if (pre[i] == 0) {
|
|||
|
|
q.push(i);
|
|||
|
|
}
|
|||
|
|
}
|
|||
|
|
|
|||
|
|
// BFS搜索
|
|||
|
|
while(!q.empty()) {
|
|||
|
|
int p = q.front();
|
|||
|
|
q.pop();
|
|||
|
|
ans.push_back(p);
|
|||
|
|
|
|||
|
|
visited[p] = 1;
|
|||
|
|
// 遍历所有以队首课程为先修课程的课程
|
|||
|
|
for (auto n: next[p]) {
|
|||
|
|
// 由于队首课程已经被修读,所以当前课程入度-1
|
|||
|
|
pre[n]--;
|
|||
|
|
// 如果该课程所有先修课程已经修完;将该课程入队
|
|||
|
|
if (pre[n] == 0) {q.push(n);}
|
|||
|
|
}
|
|||
|
|
}
|
|||
|
|
|
|||
|
|
// 环路检测: 如果仍有课程没有修读;说明环路存在
|
|||
|
|
for (int i = 0; i < numCourses; i++) {
|
|||
|
|
if (!visited[i]) return vector<int>();
|
|||
|
|
}
|
|||
|
|
|
|||
|
|
return ans;
|
|||
|
|
}
|
|||
|
|
};
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
我们用一个队列来表示所有满足修读条件的课程,一开始把所有没有先修课程的节点加入其中;再遍历出队,每次出队说明该课程已经修读过了,然后我们需要再遍历一下这个课程的所有后继课程,看看哪些在修完这门课程之后就可以修读了。
|
|||
|
|
|
|||
|
|
那哪些课程可以呢?这里我们非常聪明地用一个图的入度数组就解决了这个问题,入度,其实就是有向图上每个节点入边的数量,我们在代码里用一个计数数组就可以记录。
|
|||
|
|
|
|||
|
|
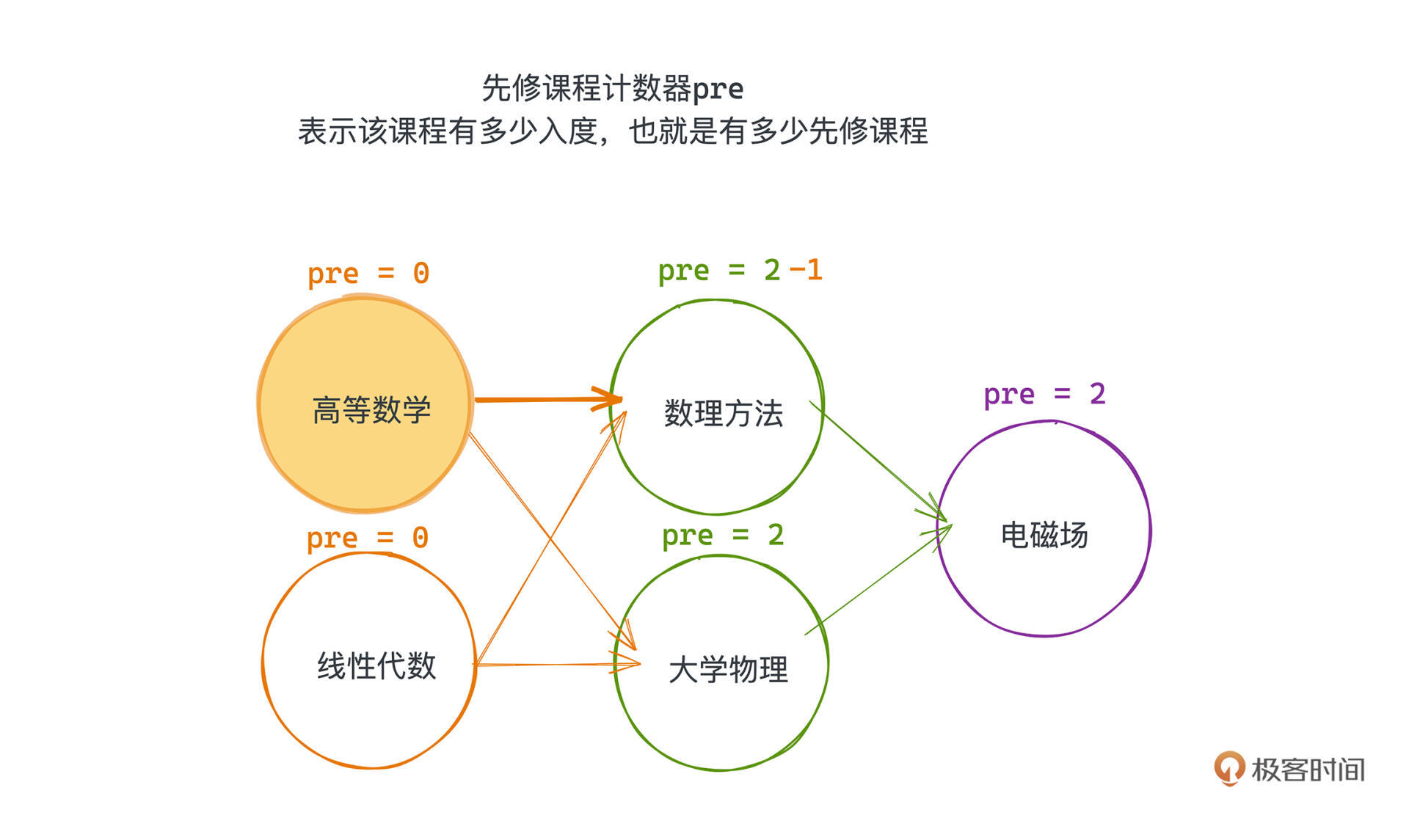
具体来说,我们给每个节点增加一个先修课程计数器pre,表示该课程有多少入度,也就是有多少先修课程,这一步操作,在遍历所有先修关系建图的时候就会完成。
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
**所以之后每修读完一门课,也就是在出队的时候,会把这门课程的先修课计数器pre进行自减操作**,如果发现哪个课程的pre已经为0了,那我们就可以把这个课程加入queue中了;因为这个时候这门课已经没有没修过的先修课程了。
|
|||
|
|
|
|||
|
|
按照这个方法遍历,所有课程的出队顺序显然就是一个合理的“拓扑序”的排列。
|
|||
|
|
|
|||
|
|
当然,我们还需要检查一下是不是所有课程都修读了,也就是代码的47-50行。如果有课程没修读完,其实就说明课表里有环存在,这不是一个合理的课表,按题目意思我们需要输出一个空集合。
|
|||
|
|
|
|||
|
|
Khan算法的全部思路和具体实现就学习到这里,如果你想更好地掌握该算法,建议你可以在力扣上找一些相关题目多做练习。
|
|||
|
|
|
|||
|
|
### dfs算法
|
|||
|
|
|
|||
|
|
通过Khan算法的学习,相信你对拓扑排序已经有了非常具体的认知,我们来看看第二种基于DFS的拓扑排序算法,这也是`html-webpack-plugin v3.2.0` 所采用的策略,它又是如何解决Webpack打包HTML chunk的排序问题的呢?
|
|||
|
|
|
|||
|
|
先上代码,注释很清晰易懂,不过由于是前端框架,你可能需要稍微花一点时间熟悉一下JavaScript的语法,不做前端的同学不用太深究具体语义,就像我们前面说的,把chunks当作有依赖关系的节点就行,和课程表中的课程其实是很像的。
|
|||
|
|
|
|||
|
|
```javascript
|
|||
|
|
/**
|
|||
|
|
Sorts dependencies between chunks by their "parents" attribute.
|
|||
|
|
|
|||
|
|
This function sorts chunks based on their dependencies with each other.
|
|||
|
|
The parent relation between chunks as generated by Webpack for each chunk
|
|||
|
|
is used to define a directed (and hopefully acyclic) graph, which is then
|
|||
|
|
topologically sorted in order to retrieve the correct order in which
|
|||
|
|
chunks need to be embedded into HTML. A directed edge in this graph is
|
|||
|
|
describing a "is parent of" relationship from a chunk to another (distinct)
|
|||
|
|
chunk. Thus topological sorting orders chunks from bottom-layer chunks to
|
|||
|
|
highest level chunks that use the lower-level chunks.
|
|||
|
|
|
|||
|
|
@param {Array} chunks an array of chunks as generated by the html-webpack-plugin.
|
|||
|
|
- For webpack < 4, It is assumed that each entry contains at least the properties
|
|||
|
|
"id" (containing the chunk id) and "parents" (array containing the ids of the
|
|||
|
|
parent chunks).
|
|||
|
|
- For webpack 4+ the see the chunkGroups param for parent-child relationships
|
|||
|
|
|
|||
|
|
@param {Array} chunks an array of ChunkGroups that has a getParents method.
|
|||
|
|
Each ChunkGroup contains a list of chunks in order.
|
|||
|
|
|
|||
|
|
@return {Array} A topologically sorted version of the input chunks
|
|||
|
|
*/
|
|||
|
|
module.exports.dependency = (chunks, options, compilation) => {
|
|||
|
|
const chunkGroups = compilation.chunkGroups;
|
|||
|
|
if (!chunks) {
|
|||
|
|
return chunks;
|
|||
|
|
}
|
|||
|
|
|
|||
|
|
// We build a map (chunk-id -> chunk) for faster access during graph building.
|
|||
|
|
const nodeMap = {};
|
|||
|
|
|
|||
|
|
chunks.forEach(chunk => {
|
|||
|
|
nodeMap[chunk.id] = chunk;
|
|||
|
|
});
|
|||
|
|
|
|||
|
|
// Next, we add an edge for each parent relationship into the graph
|
|||
|
|
let edges = [];
|
|||
|
|
|
|||
|
|
if (chunkGroups) {
|
|||
|
|
// Add an edge for each parent (parent -> child)
|
|||
|
|
edges = chunkGroups.reduce((result, chunkGroup) => result.concat(
|
|||
|
|
Array.from(chunkGroup.parentsIterable, parentGroup => [parentGroup, chunkGroup])
|
|||
|
|
), []);
|
|||
|
|
const sortedGroups = toposort.array(chunkGroups, edges);
|
|||
|
|
// flatten chunkGroup into chunks
|
|||
|
|
const sortedChunks = sortedGroups
|
|||
|
|
.reduce((result, chunkGroup) => result.concat(chunkGroup.chunks), [])
|
|||
|
|
.map(chunk => // use the chunk from the list passed in, since it may be a filtered list
|
|||
|
|
nodeMap[chunk.id])
|
|||
|
|
.filter((chunk, index, self) => {
|
|||
|
|
// make sure exists (ie excluded chunks not in nodeMap)
|
|||
|
|
const exists = !!chunk;
|
|||
|
|
// make sure we have a unique list
|
|||
|
|
const unique = self.indexOf(chunk) === index;
|
|||
|
|
return exists && unique;
|
|||
|
|
});
|
|||
|
|
return sortedChunks;
|
|||
|
|
} else {
|
|||
|
|
// before webpack 4 there was no chunkGroups
|
|||
|
|
chunks.forEach(chunk => {
|
|||
|
|
if (chunk.parents) {
|
|||
|
|
// Add an edge for each parent (parent -> child)
|
|||
|
|
chunk.parents.forEach(parentId => {
|
|||
|
|
// webpack2 chunk.parents are chunks instead of string id(s)
|
|||
|
|
const parentChunk = _.isObject(parentId) ? parentId : nodeMap[parentId];
|
|||
|
|
// If the parent chunk does not exist (e.g. because of an excluded chunk)
|
|||
|
|
// we ignore that parent
|
|||
|
|
if (parentChunk) {
|
|||
|
|
edges.push([parentChunk, chunk]);
|
|||
|
|
}
|
|||
|
|
});
|
|||
|
|
}
|
|||
|
|
});
|
|||
|
|
// We now perform a topological sorting on the input chunks and built edges
|
|||
|
|
return toposort.array(chunks, edges);
|
|||
|
|
}
|
|||
|
|
};
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
在Webpack4之前,所有的chunks是有父子关系的,你可以认为父节点是需要依赖子节点的。Webpack在生成HTML的chunks时,需要按照拓扑序的方式一次遍历打包并嵌入到最终的HTML中,这样我们就可以把后面父chunk所用到的子chunk放在更前面的位置。
|
|||
|
|
|
|||
|
|
所以,59-73行,这一段代码其实就是用来把这个问题的边表提取出来的,我们通过`forEach`方法遍历了所有的chunks,然后把父子关系全部用edges变量记录下来,这和课程表的先修数组是一样的存图方式,也就是边表。
|
|||
|
|
|
|||
|
|
有了边表,我们就要对它排序了。真正的拓扑排序代码其实在第76行,调用了toposort.array方法,这个方法来自一个js的包`toposort`,它提供了非常干净的接口,输入一个DAG的所有节点和边作为参数,返回一个合法的拓扑序。
|
|||
|
|
|
|||
|
|
具体是怎么实现的呢?我们看一下toposort包的源码:
|
|||
|
|
|
|||
|
|
```javascript
|
|||
|
|
/**
|
|||
|
|
* Topological sorting function
|
|||
|
|
*
|
|||
|
|
* @param {Array} edges
|
|||
|
|
* @returns {Array}
|
|||
|
|
*/
|
|||
|
|
|
|||
|
|
module.exports = function(edges) {
|
|||
|
|
return toposort(uniqueNodes(edges), edges)
|
|||
|
|
}
|
|||
|
|
|
|||
|
|
module.exports.array = toposort
|
|||
|
|
|
|||
|
|
function toposort(nodes, edges) {
|
|||
|
|
var cursor = nodes.length
|
|||
|
|
, sorted = new Array(cursor)
|
|||
|
|
, visited = {}
|
|||
|
|
, i = cursor
|
|||
|
|
// Better data structures make algorithm much faster.
|
|||
|
|
, outgoingEdges = makeOutgoingEdges(edges)
|
|||
|
|
, nodesHash = makeNodesHash(nodes)
|
|||
|
|
|
|||
|
|
// check for unknown nodes
|
|||
|
|
edges.forEach(function(edge) {
|
|||
|
|
if (!nodesHash.has(edge[0]) || !nodesHash.has(edge[1])) {
|
|||
|
|
throw new Error('Unknown node. There is an unknown node in the supplied edges.')
|
|||
|
|
}
|
|||
|
|
})
|
|||
|
|
|
|||
|
|
while (i--) {
|
|||
|
|
if (!visited[i]) visit(nodes[i], i, new Set())
|
|||
|
|
}
|
|||
|
|
|
|||
|
|
return sorted
|
|||
|
|
|
|||
|
|
function visit(node, i, predecessors) {
|
|||
|
|
if(predecessors.has(node)) {
|
|||
|
|
var nodeRep
|
|||
|
|
try {
|
|||
|
|
nodeRep = ", node was:" + JSON.stringify(node)
|
|||
|
|
} catch(e) {
|
|||
|
|
nodeRep = ""
|
|||
|
|
}
|
|||
|
|
throw new Error('Cyclic dependency' + nodeRep)
|
|||
|
|
}
|
|||
|
|
|
|||
|
|
if (!nodesHash.has(node)) {
|
|||
|
|
throw new Error('Found unknown node. Make sure to provided all involved nodes. Unknown node: '+JSON.stringify(node))
|
|||
|
|
}
|
|||
|
|
|
|||
|
|
if (visited[i]) return;
|
|||
|
|
visited[i] = true
|
|||
|
|
|
|||
|
|
var outgoing = outgoingEdges.get(node) || new Set()
|
|||
|
|
outgoing = Array.from(outgoing)
|
|||
|
|
|
|||
|
|
if (i = outgoing.length) {
|
|||
|
|
predecessors.add(node)
|
|||
|
|
do {
|
|||
|
|
var child = outgoing[--i]
|
|||
|
|
visit(child, nodesHash.get(child), predecessors)
|
|||
|
|
} while (i)
|
|||
|
|
predecessors.delete(node)
|
|||
|
|
}
|
|||
|
|
|
|||
|
|
sorted[--cursor] = node
|
|||
|
|
}
|
|||
|
|
}
|
|||
|
|
|
|||
|
|
function uniqueNodes(arr){
|
|||
|
|
var res = new Set()
|
|||
|
|
for (var i = 0, len = arr.length; i < len; i++) {
|
|||
|
|
var edge = arr[i]
|
|||
|
|
res.add(edge[0])
|
|||
|
|
res.add(edge[1])
|
|||
|
|
}
|
|||
|
|
return Array.from(res)
|
|||
|
|
}
|
|||
|
|
|
|||
|
|
function makeOutgoingEdges(arr){
|
|||
|
|
var edges = new Map()
|
|||
|
|
for (var i = 0, len = arr.length; i < len; i++) {
|
|||
|
|
var edge = arr[i]
|
|||
|
|
if (!edges.has(edge[0])) edges.set(edge[0], new Set())
|
|||
|
|
if (!edges.has(edge[1])) edges.set(edge[1], new Set())
|
|||
|
|
edges.get(edge[0]).add(edge[1])
|
|||
|
|
}
|
|||
|
|
return edges
|
|||
|
|
}
|
|||
|
|
|
|||
|
|
function makeNodesHash(arr){
|
|||
|
|
var res = new Map()
|
|||
|
|
for (var i = 0, len = arr.length; i < len; i++) {
|
|||
|
|
res.set(arr[i], i)
|
|||
|
|
}
|
|||
|
|
return res
|
|||
|
|
}
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
这个代码虽然不是很长,但还是没有那么好理解,我会把一些核心的逻辑讲解一下,你再对着看应该就很清晰了。
|
|||
|
|
|
|||
|
|
基于DFS的思路,和BFS优先选择所有可修读课的策略,就是完全不一样的两个极端。**在DFS策略中,我们优先找出没有后继课程的节点,把它作为最后修读的课程**,这样一定可以保证在DAG中的拓扑序中它是安全的,因为所有它依赖的节点一定在它之前。
|
|||
|
|
|
|||
|
|
那如何找呢?在DFS的策略中,我们需要几个关键变量,对应在toposort的代码里分别是:
|
|||
|
|
|
|||
|
|
1. 数组visited:用来标记某个节点是不是已经遍历过;只要是遍历过的节点,就不再重复遍历。
|
|||
|
|
2. 数组sorted:用于存放最后拓扑序的结果集。
|
|||
|
|
|
|||
|
|
在DFS拓扑排序算法的传统讲解中可能会用一个栈来表示sorted这个结构。这里toposort包用了数组,让插入的顺序是从数组尾部开始,其实就是模拟了栈的结构。
|
|||
|
|
|
|||
|
|
之所以用栈,就是为了**在DFS过程中把我们碰到的所有没有子节点的元素,按照先进后出的顺序维护,让这些节点在拓扑序中更靠前**。
|
|||
|
|
|
|||
|
|
3. outgoingEdges数组:这也是一个基于数组实现的邻接表的实例。
|
|||
|
|
4. predecessors集合:这也是一个非常重要的变量,用于在DFS的过程里帮助我们判断是否有环。
|
|||
|
|
|
|||
|
|
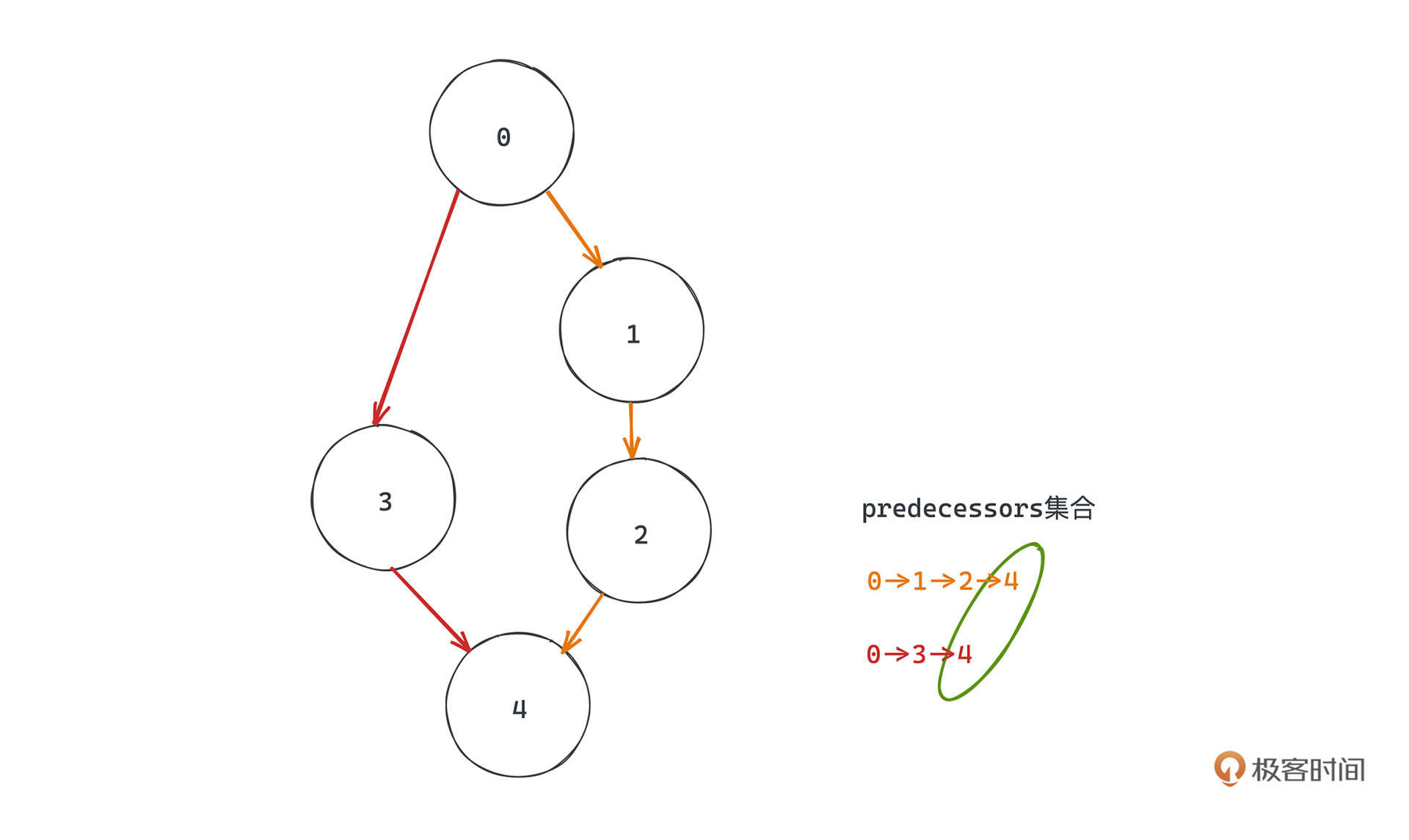
怎么判断有环呢,其实很简单,从某个节点出发,如果发现在这次遍历的某个路径中能遍历到已经出现过的节点,就说明有环路存在了。具体来说,我们用predecessors把DFS过程中出现的元素记录下来就可以了。
|
|||
|
|
|
|||
|
|
当然DFS结束之后还需要注意恢复现场,就是说**在一条路径调用完成之后,要把predecessors之前加进去的节点都移除**,这是因为在有向图中两条路径可能有交集,但并不一定构成环。比如这个例子,红色路径和黄色路径都经过最下面的节点,如果不恢复现场在某次DFS中就会出现重叠。
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
整个拓扑排序的过程,也就非常清晰,我们遍历所有节点,按照什么顺序都可以;然后从每个节点开始,沿着其有向边进行DFS的图遍历,遍历过的节点都会被visited记录遍历状态,保证不会重复遍历。
|
|||
|
|
|
|||
|
|
如果某个节点的子节点全部被visit函数DFS完毕,我们就会把当前节点加入栈中。因为当前节点子节点全部DFS完毕就意味着,所有依赖当前节点的节点都已经在栈中放到了该节点之后,于是只要能保证如果图中没有环,整个过程结束后,把栈里的元素自顶而下排列就是满足“拓扑序”的。
|
|||
|
|
|
|||
|
|
对着详细的说明,你重点看代码的36-68行,多看几遍代码应该就很好理解啦。
|
|||
|
|
|
|||
|
|
这就是第二种基于DFS的拓扑排序算法的思路,递归处理所有节点,采用先输出依赖自己的节点、再输出自己的策略来保证拓扑序。在早期的Webpack中就是这样处理chunk之间的打包顺序的。
|
|||
|
|
|
|||
|
|
### 复杂度
|
|||
|
|
|
|||
|
|
那么这两种算法的复杂度是多少呢?
|
|||
|
|
|
|||
|
|
首先khan算法,BFS的过程中把所有节点一一入队、再一一出队,搜索过程中每条边也会被遍历一次,所以对于有V个顶点E条边的图,整体的时间复杂度是O(V+E)。空间复杂度主要引入了额外的队列、各个顶点是否被访问的标记,以及记录了所有边信息的邻接表,所以空间复杂度同样和顶点数还有边数成线性关系,为O(V+E)。
|
|||
|
|
|
|||
|
|
基于DFS的算法,时间复杂度上其实和BFS差不多,在DFS过程中每个顶点、每条边也都会被遍历到,整体时间复杂度同样为O(V+E),空间上也有邻接表和访问记录等信息为O(V+E)。
|
|||
|
|
|
|||
|
|
## 总结
|
|||
|
|
|
|||
|
|
相信通过今天的学习,你已经了解了Webpack在打包HTML的时候是如何对chunk排序了吧,本质上就是一个对有向无环图输出节点“拓扑序”排列的问题。
|
|||
|
|
|
|||
|
|
在计算机的世界里,这样输出拓扑序的需求其实随处可见,不信你仔细想一想平时用brew或者apt-get装包的时候计算机都会做哪些事情呢?一个包可能依赖了许许多多不同的包,计算机是从哪个包开始装起的呢?相信你学了今天拓扑排序的两个算法,应该就知道怎么做了吧。
|
|||
|
|
|
|||
|
|
利用拓扑排序的算法,我们也可以来确定整个图中是否有环。在khan算法中,我们通过贪心算法把所有能输出到拓扑序的节点都输出,如果发现图中还有节点没有被输出的话,就可以说明它们一定在某个环路中了。而在DFS中如何做呢,前面其实我们也提到过,如果在DFS的过程中访问到一个已经被访问过且不是上一步之前被访问的节点,就说明环存在。
|
|||
|
|
|
|||
|
|
## 课后作业
|
|||
|
|
|
|||
|
|
如果只是要判断环路而不需要输出拓扑序的话,我们是否有效率更高的办法?你可以实现一下吗?
|
|||
|
|
|
|||
|
|
欢迎你在评论区留言和我讨论。如果有收获也欢迎你转发给身边的朋友,邀他一起学习。我们下节课见~
|
|||
|
|
|
|||
|
|
### 参考资料
|
|||
|
|
|
|||
|
|
你可能会疑惑,为什么选择了v3.2.0这个相对较老的版本?主要是因为Webpack4.0之后引入了chunkGroup的概念,用 `SplitChunksPlugin` 替换了 `CommonsChunkPlugin`,代码中不再需要对chunk进行拓扑排序了。
|
|||
|
|
|