318 lines
24 KiB
Markdown
318 lines
24 KiB
Markdown
|
|
# 先导篇|诶,这个 git diff 好像不是很直观?
|
|||
|
|
|
|||
|
|
你好,我是微扰君。
|
|||
|
|
|
|||
|
|
相信你每天都会使用Git,作为一款免费、开源的分布式版本控制系统,Git最初是 Linus Torvalds 为了帮助管理 Linux 内核开源协作而开发的,随着GitHub的流行和Git本身的系统优势,它也渐渐成为我们广大研发人员日常工作中必不可少的版本管理利器。
|
|||
|
|
|
|||
|
|
在使用Git的过程中,你一定会常常用到 git diff 的命令,去查看这次待提交的本地代码和修改前的代码有什么区别,确定没有问题才会进行 commit 操作。像 git diff 这样求解两段文本差异的问题,我们一般称为“文本差分”问题。
|
|||
|
|
|
|||
|
|
但是不知道你有没有思考过文本差分的算法是怎么实现的呢?
|
|||
|
|
|
|||
|
|
如果你现在静下心来思考一下,就会发现**写出一个简明的文本差分算法并不是一件非常容易的事情**。因为代码的文本差分展现形式可能有很多,但并不一定都有非常好的可读性。
|
|||
|
|
|
|||
|
|
而 git diff 给我们展示的,恰恰是比较符合人们阅读习惯且简明的方式,简明到让我们即使天天都在使用这个功能也不会有意识地去思考:“诶,这个difference生成的好像不是很清晰?是怎么做的呢?”。
|
|||
|
|
|
|||
|
|
就让我们从这样一个“简单”、有趣、常用的文本差分算法开始,探索那些其实就在我们身边却常常被熟视无睹的算法们吧。希望能给你一些启发,而且探索算法思想的过程也会非常有趣(如果你在学习这一讲的过程中觉得有点难,最后我们会揭秘原因)。
|
|||
|
|
|
|||
|
|
## 文本差分是什么
|
|||
|
|
|
|||
|
|
文本差分算法其实是一个历史悠久的经典算法问题,许多学者都有相关的研究,解决这个问题的思路也是百家争鸣,复杂度相差甚远。
|
|||
|
|
|
|||
|
|
而在git diff的实现里,其实就内置有多个不同的diff算法,我们今天主要介绍的是git diff的默认算法:Myers 差分算法,这是一个相对简单、效率高且直观的文本差分算法([原论文](http://www.xmailserver.org/diff2.pdf))。
|
|||
|
|
|
|||
|
|
在学习这个算法之前,我们得首先来定义一下什么是文本差分(difference),毕竟这个词本身就不是那么直观。
|
|||
|
|
|
|||
|
|
我们找原始出处,Myers在论文中,提到了这样一句话:
|
|||
|
|
|
|||
|
|
> An edit script for A and B is a set of insertion and deletion commands that transform A into B.
|
|||
|
|
|
|||
|
|
其中有一个概念叫作 edit script,也就是编辑脚本。比如,对于源文本A和目标文本B,我们一定可以通过不断执行删除行和插入行两种操作,使得A转化成B,这样的一系列插入和删除操作的序列就被称作编辑脚本。**所以,文本差分算法,可以定义为用于求出输入源文本和目标文本之间的编辑脚本的算法,**广泛运用于各种需要进行文本对比的地方。
|
|||
|
|
|
|||
|
|
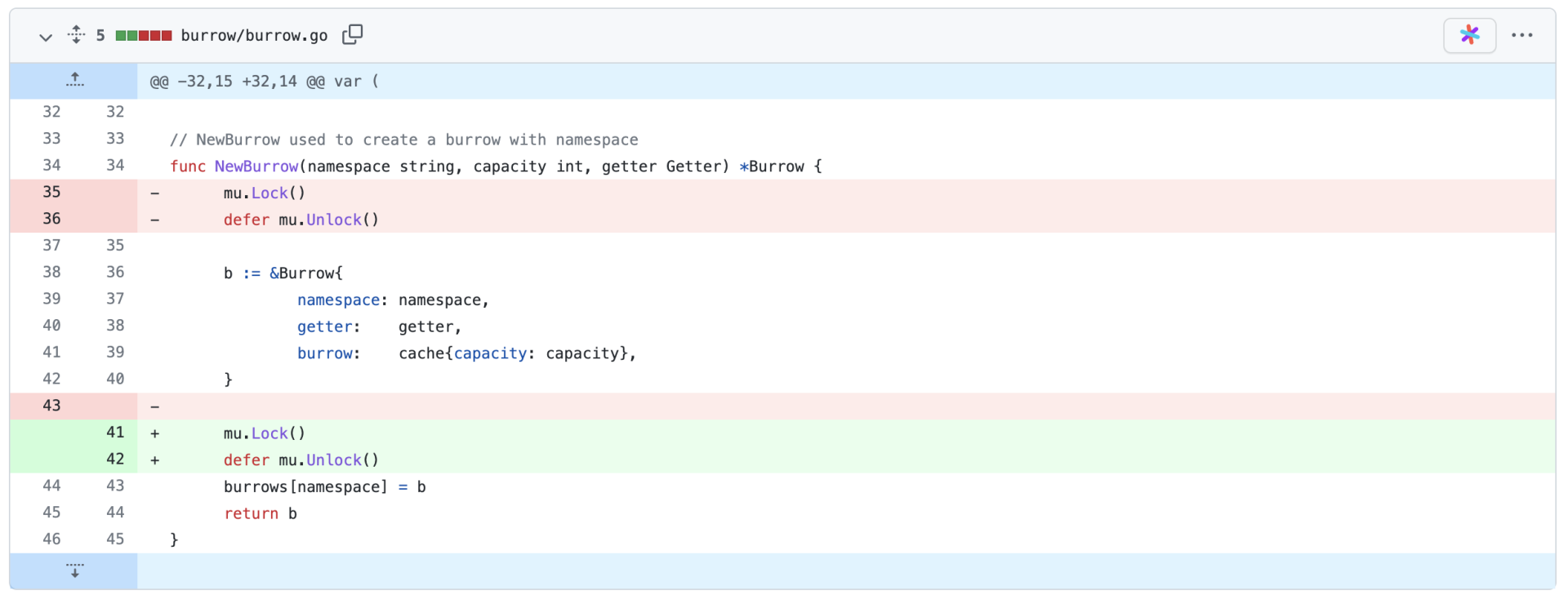
比如,git diff 就是一个很经典的应用场景,下图是一个真实的例子(具体的commit可以在[这里](https://github.com/wfnuser/burrow/commit/4edc0deaec9e83e6d4bf024cf82f0b4f96521e80)找到)。
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
但是,两个文本之间的差分方式可能远远不止一种。
|
|||
|
|
|
|||
|
|
比如说,对于任意两个文本A和B,我们总是可以通过将源文本逐行全部删去,再逐行添加目标文本的方式来做变换,也可以通过只修改差异部分的方式,做从A到B的变换,比如上面的例子中所展示的这样。
|
|||
|
|
|
|||
|
|
那我们如何评价不同编辑脚本之间的优劣呢?
|
|||
|
|
|
|||
|
|
## 评价指标1
|
|||
|
|
|
|||
|
|
第一个评价指标,其实也不难想到就是:**编辑脚本的长度**。
|
|||
|
|
|
|||
|
|
我们举一个论文中的例子来讨论,后面大部分讨论也都会基于这个例子展开:
|
|||
|
|
|
|||
|
|
```plain
|
|||
|
|
源序列 S = ABCABBA 目标序列 T = CBABAC
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
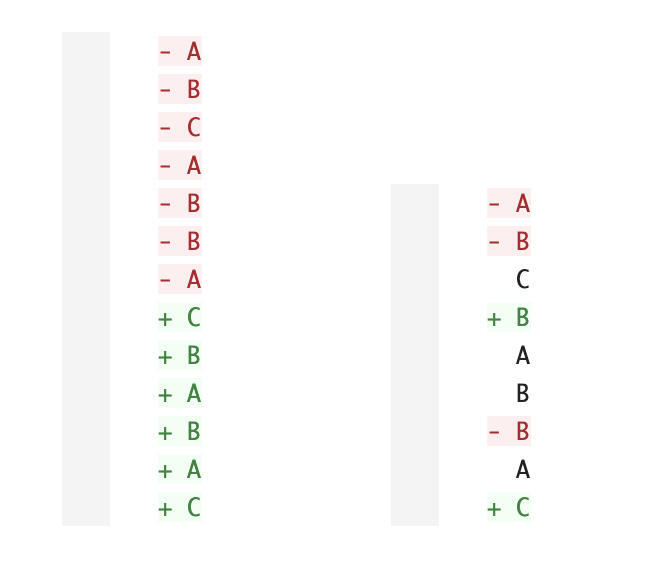
想要完成从S到T的变换,图中左边的编辑脚本就是前面所说的先删后添的方式,并没有体现出两个文档之间的修改点,显然不是一个很直观的变换表示;而右边的编辑脚本就明显好得多。
|
|||
|
|
|
|||
|
|
|
|||
|
|
直观地来说,右边的编辑脚本要比左边短的多,因为它尽可能保留了更多的原序列中的元素。
|
|||
|
|
|
|||
|
|
所以,一种符合直觉的文本差分算法的衡量指标,就是其**编辑脚本的长度,长度越短越好**。我们一会要介绍的Myers算法,也是在求一种最短的编辑脚本(也就是SES Shortest Edit Script)的算法。
|
|||
|
|
|
|||
|
|
但是SES要怎么求呢?原论文中也提到,最短编辑距离问题也就是SES,和最长公共子序列问题也就是LCS其实是一对对偶问题,如果求得其中一个问题的解等同于找到了另一个问题的解。
|
|||
|
|
|
|||
|
|
而最长公共子序列问题,相信许多准备过面试的同学都有所了解吧。大部分算法面试题中要求的解法复杂度是O(N\*LogN),采用动态规划就可以解决。不过呢,这并不是今天的重点,先不展开具体算法了。
|
|||
|
|
|
|||
|
|
这里我们简短地说明一下两个问题的关联性,还是用刚才的例子:
|
|||
|
|
|
|||
|
|
```plain
|
|||
|
|
源序列
|
|||
|
|
S = ABCABBA length m = 7
|
|||
|
|
目标序列
|
|||
|
|
T = CBABAC length n = 6
|
|||
|
|
|
|||
|
|
最长公共子序列(不唯一)
|
|||
|
|
C = CBBA length LC = 4
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
我们很容易发现最短的编辑脚本的长度就等于 _m + n - 2 \* LC_ 。其中,M和N为原序列S和目标序列T的长度,LC为最长公共子序列的长度。这是因为在从原序列到目标序列的变化过程中,**两者的最长公共子序列中的元素我们都是可以保留的**,只需要在编辑脚本里,按顺序分别删除原序列和插入目标序列里不在公共序列中的元素即可。
|
|||
|
|
|
|||
|
|
当然,两个序列的最长公共子序列往往也不唯一,不同的最长公共子序列都对应着不同的编辑脚本产生,但这些编辑脚本一定都是最短的。
|
|||
|
|
|
|||
|
|
## 评价指标2
|
|||
|
|
|
|||
|
|
那只是找到A到B的最短编辑脚本,我们就能满意了吗?并不能,因为即使编辑脚本长度一样,由于删除和插入的顺序不同,人们理解它的难度也会不同。所以,**这里就需要引入第二个指标:可读性**,毕竟文本的编辑脚本往往最终是要展示给用户看的。
|
|||
|
|
|
|||
|
|
这当然是一个很笼统的讲法,我们再借用刚才的例子,来直观地比较一下不同方式的区别吧。
|
|||
|
|
|
|||
|
|
```go
|
|||
|
|
源序列
|
|||
|
|
S = ABCABBA
|
|||
|
|
目标序列
|
|||
|
|
T = CBABAC
|
|||
|
|
1. - A 2. - A 3. + C
|
|||
|
|
- B + C - A
|
|||
|
|
C B B
|
|||
|
|
- A - C - C
|
|||
|
|
B A A
|
|||
|
|
+ A B B
|
|||
|
|
B - B - B
|
|||
|
|
A A A
|
|||
|
|
+ C + C + C
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
从S变化到T,我们至少可以得到这三种编辑脚本,都是最短的编辑脚本。相信你仔细观察一下之后,可能会有一种感觉,就是第一种比后面两种可读性会好一些,因为删去的行和增加的行并没有彼此交叉,所以可以更清晰地看出修改的代码是哪些。
|
|||
|
|
|
|||
|
|
下面这个例子感受可能更明显一点:
|
|||
|
|
|
|||
|
|
```plain
|
|||
|
|
Good: - aaa Bad: + ddd
|
|||
|
|
- bbb - aaa
|
|||
|
|
- ccc + eee
|
|||
|
|
+ ddd - bbb
|
|||
|
|
+ eee - ccc
|
|||
|
|
+ fff + fff
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
对于整段的代码修改来说,左侧对于大部分人来说往往是更清晰的一种展示方式。编辑长度相同的前提下,左侧之所以“更清晰”的直观感受可以总结为两点:
|
|||
|
|
|
|||
|
|
1. 我们希望尽可能多地保留整段文本,尽可能连续地删除和插入操作,而不是彼此交叉。
|
|||
|
|
2. 大部分人可能更习惯先看到原文本的删除,再看到目标文本的插入。
|
|||
|
|
|
|||
|
|
Myers也是这么觉得的,所以他提出了一种贪心的策略,可以让我们大部分时候得到一个最短且“质量高”的编辑脚本。策略的逻辑就是,**在最短的编辑脚本里,尽量找到删除在增加前面,且尽可能多地连续删除更多行的方式**。
|
|||
|
|
|
|||
|
|
直觉上来说,这就能避免许多交叉的修改,将整段代码的添加更直观地展现给用户;当然这也并不是绝对的,只能说在大部分情况下都更加直观一些。
|
|||
|
|
|
|||
|
|
到底如何找到最短编辑脚本中比较直观的一个?这就是Myers算法的用武之地啦,下面我们就来看看Myers为了解决这个问题所做的独特抽象和建模,这是理解Myers算法的关键。
|
|||
|
|
|
|||
|
|
## Myers Diff Algorithm 模型抽象
|
|||
|
|
|
|||
|
|
正如前面提到的,从源序列S到目标序列T,有两种操作,分别是删除行和插入行。
|
|||
|
|
|
|||
|
|
```plain
|
|||
|
|
源序列
|
|||
|
|
S = ABCABBA length m = 7
|
|||
|
|
目标序列
|
|||
|
|
T = CBABAC length n = 6
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
现在我们就需要找到一种对这两个操作和相应变换状态的抽象方式,帮助我们更好地将问题转化成可以被编程语言实现的代码。
|
|||
|
|
|
|||
|
|
### 如何抽象-转化为图搜索问题
|
|||
|
|
|
|||
|
|
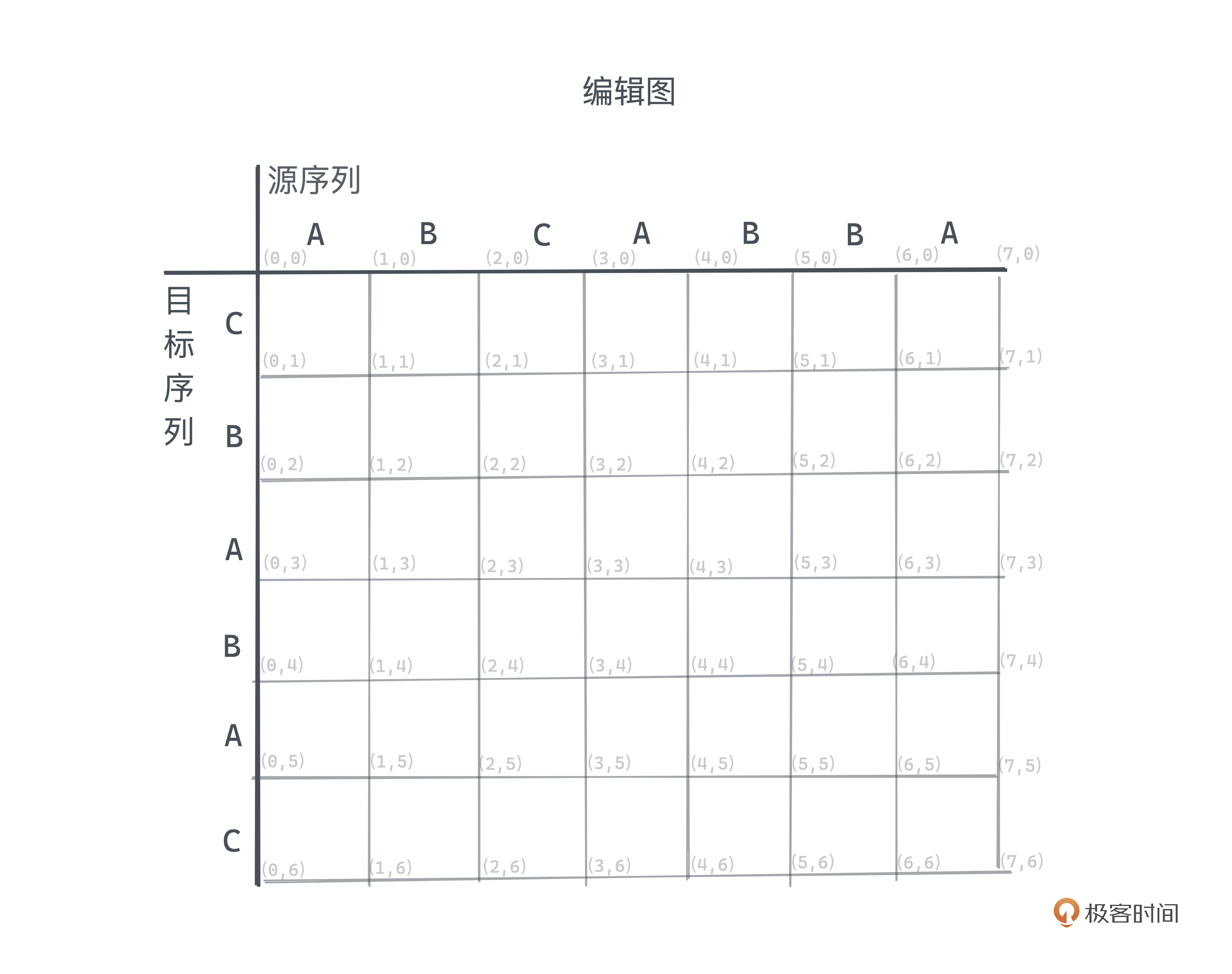
Myers采用了一种非常独特的视角,将这个问题很好地转化为了一个图上的搜索问题。具体做法是这样的:建立一个放在二维平面的网格,网格宽度为m+1,高度为n+1,如下图所示,在坐标系中,X轴向右侧延伸,Y轴则向下延伸。其中横轴代表着源序列,而纵轴代表着目标序列。我们把这张图称为编辑图。
|
|||
|
|
|
|||
|
|
具体什么意思呢? 我们还是看之前那个例子的编辑图:
|
|||
|
|
|
|||
|
|
|
|||
|
|
看图上的坐标, (0, 0) 这个点,代表什么操作都没有做的初始状态,而(7, 6)则对应了最终完整的从S到T的编辑脚本。
|
|||
|
|
|
|||
|
|
我们从(0, 0)出发进行图上的搜索,每次经过网格中所有的**横线代表的是删除操作**,如经过(0,0) -> (1,0) 的横线,代表了将S的第一个字符A删去。与之相对地,经过所有的**竖线则代表着插入操作**,如 (3,3) -> (3,4) 代表着对T中的第4个字符B进行插入操作。
|
|||
|
|
|
|||
|
|
显然,网格中的这些横线或竖线的权重为1,因为每次删除和插入操作所需要花费的操作数都是一样的,我们就记为1。而二维网格从原点出发到每一个坐标的路径,都对应着一段不完全的编辑脚本,也代表着从原文本到目标文本某种变换的一个中间状态。
|
|||
|
|
|
|||
|
|
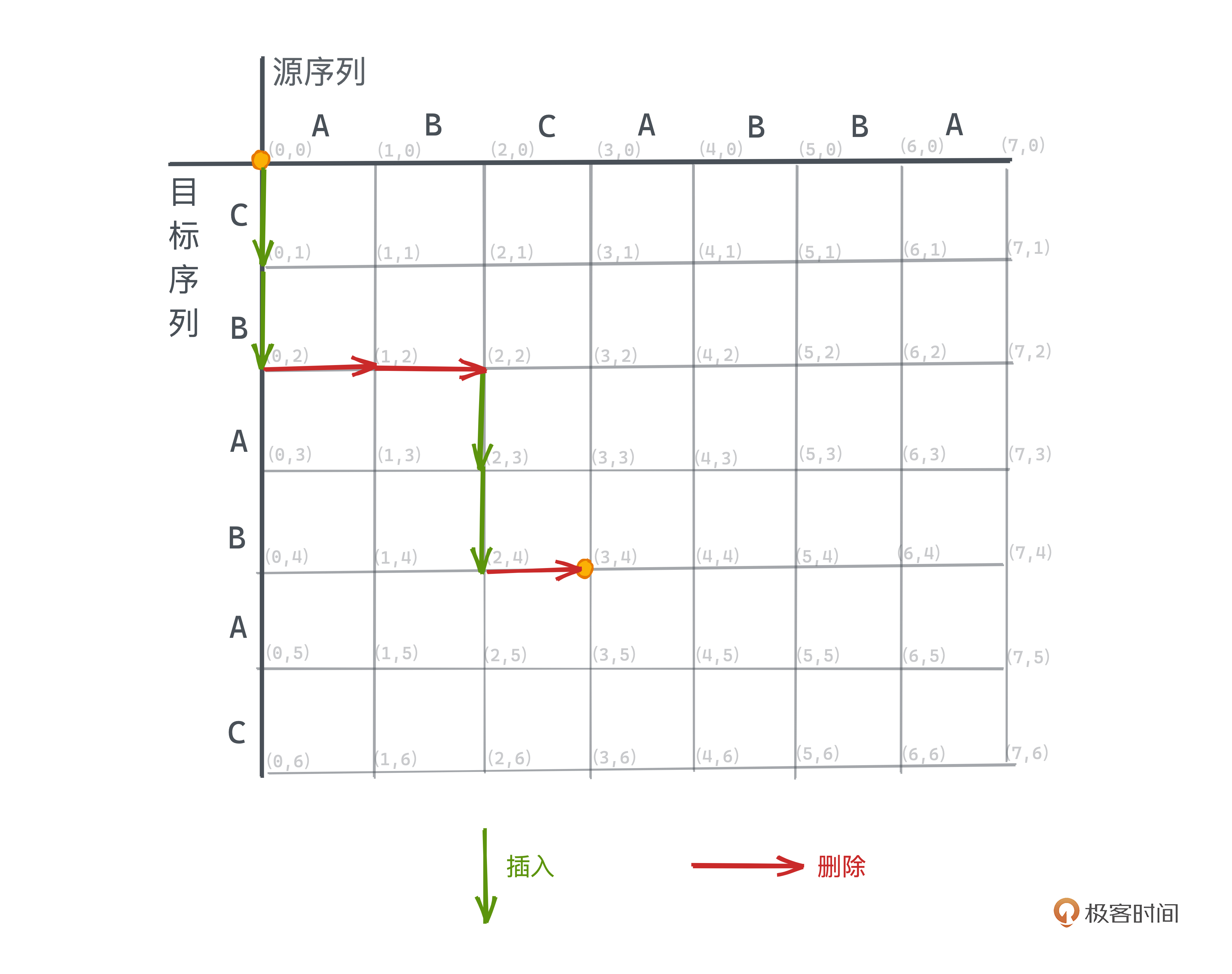
比如下图中从 (0,0) -> (3,4) 的路径就表示着字符串ABC -> CBAB的一种编辑方式,我们先插入CB,然后删除AB再插入AB,最后删除C。这是完整路径中的一部分,也就是完整编辑脚本的一部分。
|
|||
|
|
|
|||
|
|
|
|||
|
|
就此,文本差分问题成功转化成了,**如何在这样的网格中找到仅允许向下和向右移动的一个从(0,0)出发到(m,n)的路径**,路径的长度就代表了总共需要的操作数。
|
|||
|
|
|
|||
|
|
比如之前的,先将源序列字符逐一删除,再将目标序列逐一添加的方式,在图中的表现形式就是从(0,0)出发一路往右,走到(m,0),随后一路向下走到(m,n),这样的总操作数就是m+n=13,等于路径中所有横线的数量和竖线的数量之和,这对应着众多最长的编辑脚本中的一种。
|
|||
|
|
|
|||
|
|
前面我们也说过,并不是所有出现在S中的字符都要删除的,可以证明所有出现在最长公共子序列中的字符,都是可以被保留下来的。那可以保留的字符,我们在图中又要如何表现呢?
|
|||
|
|
|
|||
|
|
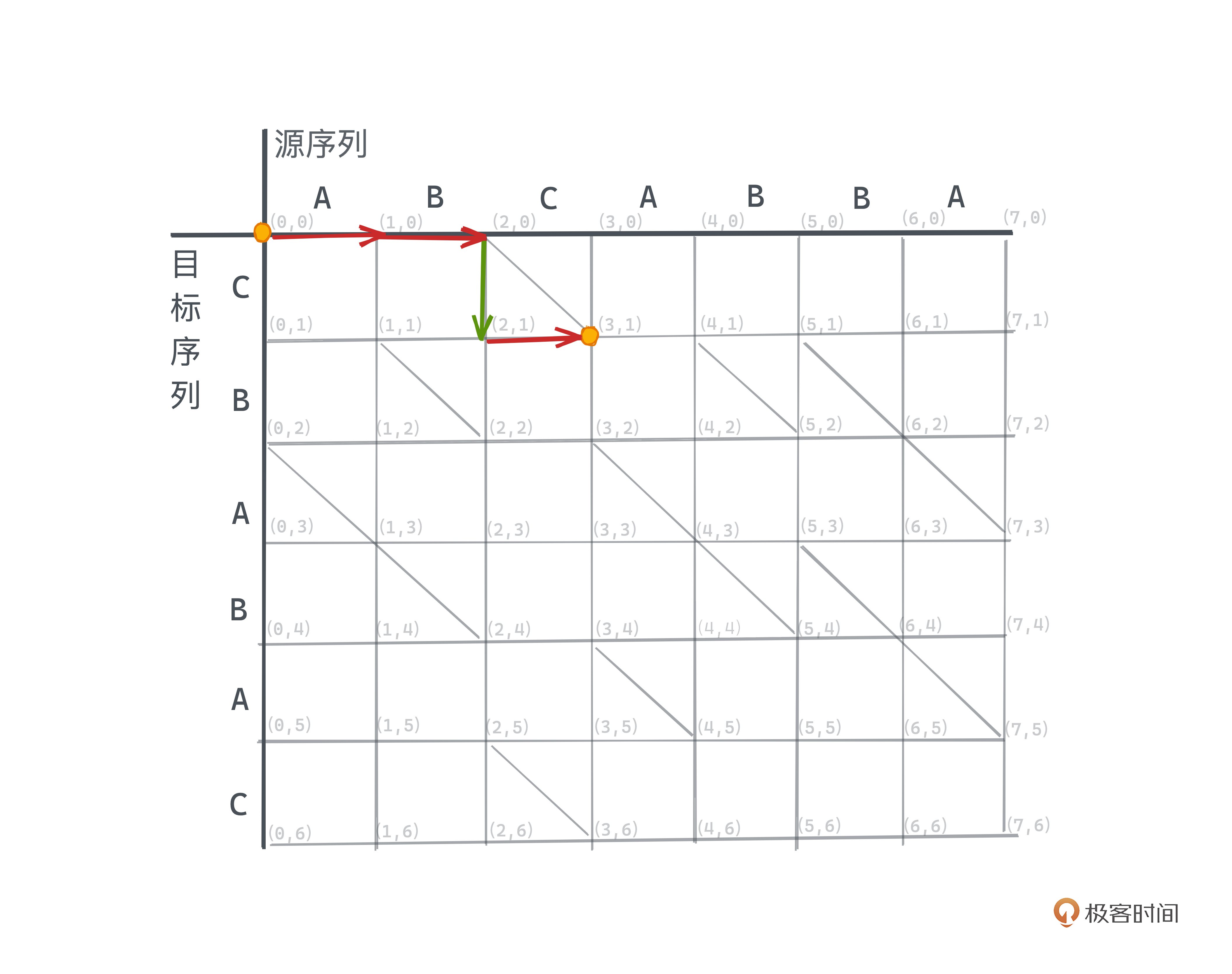
比如为了从 (2,0)转移到 (3,1) ,我们当然可以先经过一个竖线,再经过一个横线,对应到脚本上也就是先插入目标序列T中的C,再删除源序列S中的C,这显然是没有意义的操作。所以,我们应该选择跳过这步操作而保留原有字符串中的C。
|
|||
|
|
|
|||
|
|
|
|||
|
|
Myers在图上这样描述保留字符的操作:我们在网格里加入一些以相同字符所对应的坐标为起点的斜线,比如图中(2,0) -> (3,1)的斜线,并且经过斜线所需要的操作数应该计为0,因为我们不需要在编辑脚本中进行插入或者删除操作。
|
|||
|
|
|
|||
|
|
所以,在编辑图中,**所有源序列和目标序列字符相等的坐标,如(2,0)和(3,1)、(4,1)和(5,2)等,我们都会有一条从上一状态(x-1,y-1)到这一状态(x,y)的斜经过,且穿过斜线路径不耗费任何操作数**。
|
|||
|
|
|
|||
|
|
至此,我们终于可以完美地将两个评价指标在图模型中量化出来。
|
|||
|
|
|
|||
|
|
1. 寻找一个最短的编辑脚本,等同于在编辑图上找到从(0,0)出发到(m,n)的最短路径。
|
|||
|
|
2. 而可读性则要求我们通过一定的策略,从最短路径中找到一个更符合人们阅读习惯的增删序列。
|
|||
|
|
|
|||
|
|
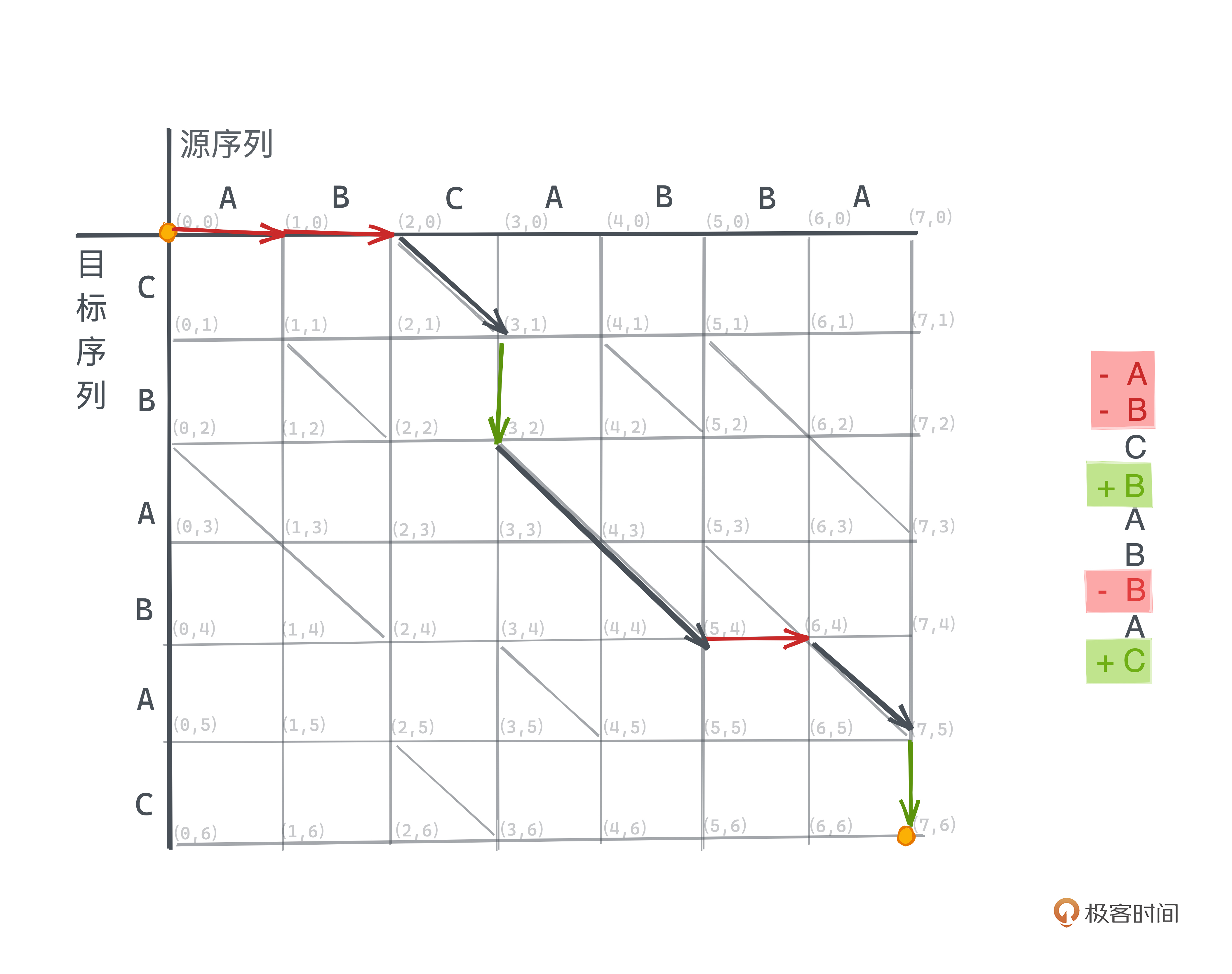
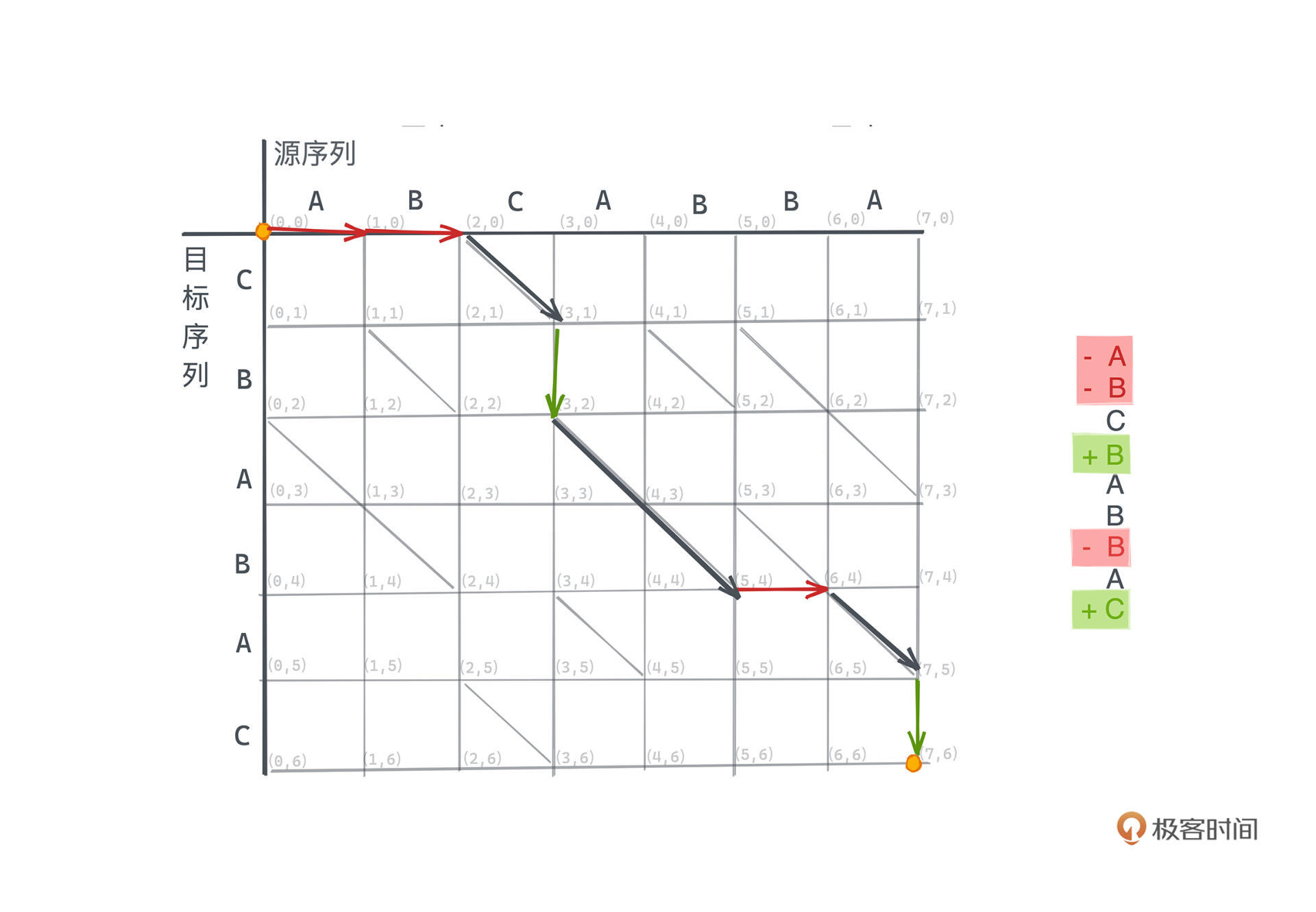
还是用这个例子,你可以直观地理解在编辑图上具体的搜索过程。图中粗箭头所示的路径,即为一条最短的路径,其对编辑脚本操作如下:
|
|||
|
|
|
|||
|
|
|
|||
|
|
由于编辑图是一个有权的图,我们所求的问题可以认为是一种特化的**单源最短路问题(SSSP问题),即求解一个有权图中,从指定源点出发到某个其他点的最短路径问题**。常用的算法包括Dijkstra、SPFA、Bellman Ford等,这些算法复杂度比较高,我们之后会在网络篇展开讲解。
|
|||
|
|
|
|||
|
|
回到这里的编辑图搜索问题,因为图中的边权只有1和0两种,我们当然可以找到更高效的算法来处理。
|
|||
|
|
|
|||
|
|
### 如何解决图搜索问题
|
|||
|
|
|
|||
|
|
Myers 就通过动态规划思想很好地解决了这个问题。下面就让我们来看一下他是怎么做的,使得找到的路径既是最短的,也是在大部分情况下非常可读的。
|
|||
|
|
|
|||
|
|
为了方便进一步表述和建模,首先学习Myers在论文中定义的几个重要概念。
|
|||
|
|
|
|||
|
|
* D-Path
|
|||
|
|
|
|||
|
|
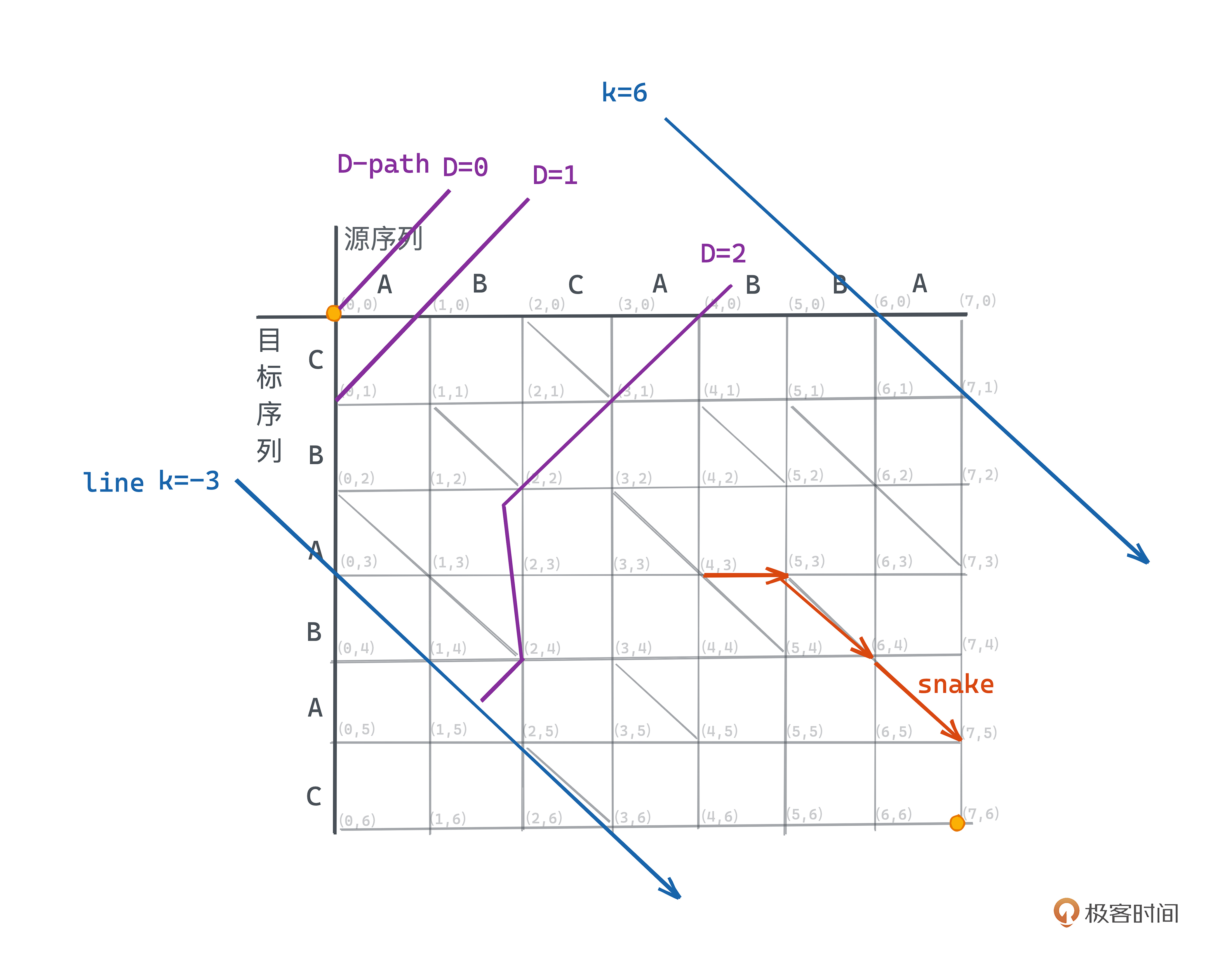
在编辑图中,路径长度对应着每一条横线或竖线需要花费的操作数之和,也就对应着编辑脚本中增删的行数。为了方便描述,我们把需要D步操作的路径称为D-Path,一条D-path指向一个经过D次增或删操作的变换过程的中间状态。
|
|||
|
|
|
|||
|
|
|
|||
|
|
* Snake
|
|||
|
|
|
|||
|
|
斜线都是不需要操作数的。我们定义一个横线或者竖线之后紧跟着0条或n条斜线所形成的路径称为snake,所以一条snake所需要的操作数为1。而且我们规定,snake结尾坐标后继不能为斜线,也就是如果snake路径中某个坐标后面有斜线,我们就会继续沿着斜线走,直到走不了为止。比如 1,0 -> 2,0 -> 3,1 就是一条snake,而1,0->2,0 就不是一条snake。
|
|||
|
|
|
|||
|
|
* Line
|
|||
|
|
|
|||
|
|
每个坐标都在一条从左上到右下45度角的斜线上。我们可以用k=x-y来描述这条斜线,在m\*n的网格中,k的取值范围为\[m,-n\]。比如坐标(2,4)和(1,3)在Line(-2)上,(3,0)和(5,2)在Line(3)上。
|
|||
|
|
|
|||
|
|
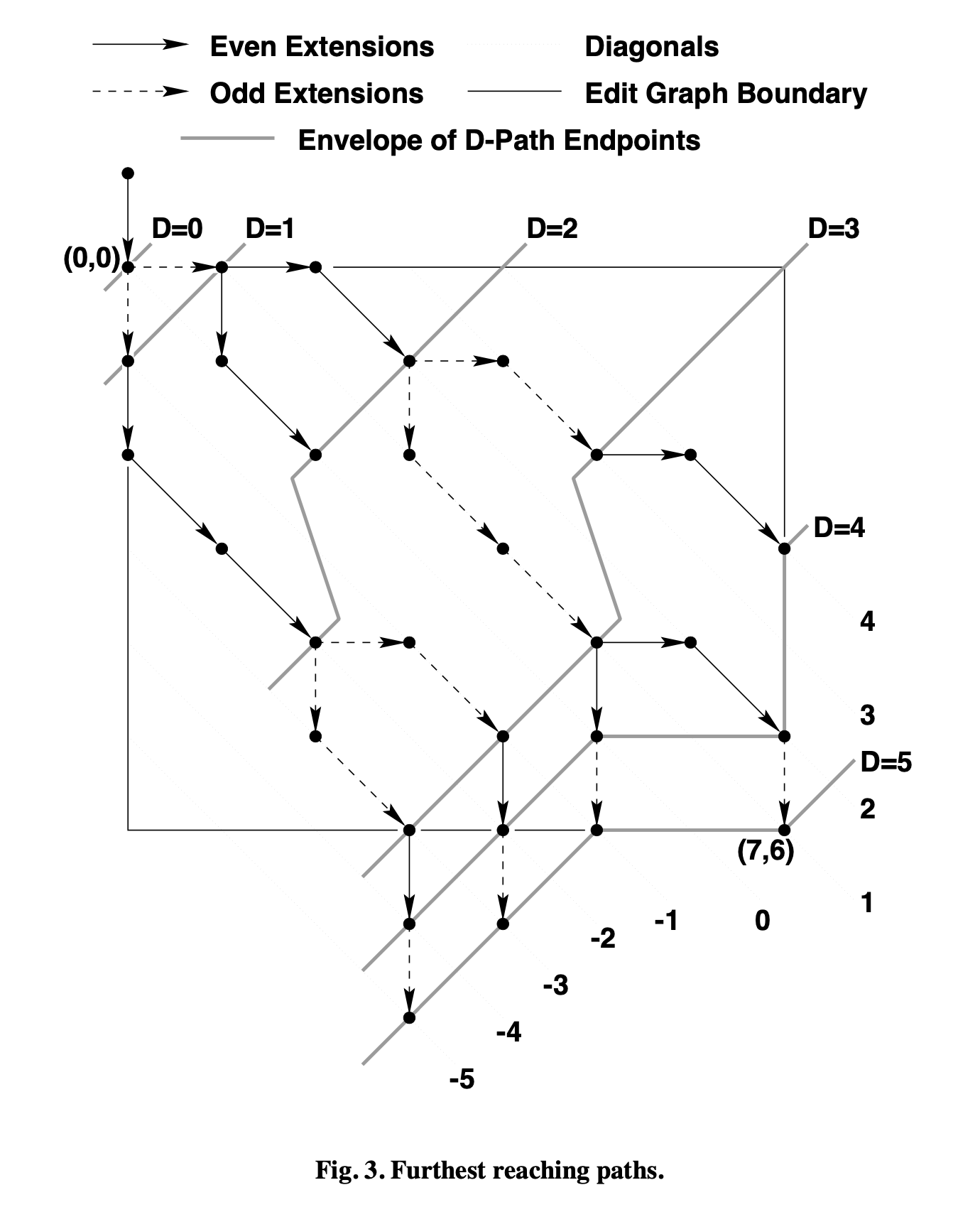
Myers 论文里的这张图就是对这几个概念的一个示意:
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
有了这些概念的定义之后,我们求解最短编辑脚本的目标就可以定义为要找到**最短的可以抵达 (m,n) 的 D-Path**。
|
|||
|
|
|
|||
|
|
由于所有的 D-Path 都是由 (D-1)-Path 接上一条 snake 构成 (也就是说,所有的编辑脚本都是由一个更短的、指向某个中间状态的脚本,加上一次增删和若干行保留操作所产生的)。
|
|||
|
|
|
|||
|
|
所以,很自然产生的一种想法就是从1-Path开始,去搜索所有和1-Path相接的2-Path看看最远能走到哪里,然后以此为基础一直递推到D-Path,当我们在搜索过程中第一次遇到终点,也就是(m, n)时,就找到最短编辑脚本路径了。这样自底向上,通过先解决子问题,逐步递推出问题的解,就是典型的动态规划思想,我们之后也会专门展开讲解。
|
|||
|
|
|
|||
|
|
**第二个指标可读性,就是假设有多条D-Path都可以抵达(m,n),我们如何从里面选出可读简明的路径呢**?Myers采取的是一种贪心的策略,背后的思想主要就是前面讲过的,Myers认为更简明的Diff操作有以下特征:
|
|||
|
|
|
|||
|
|
1. 我们希望尽可能多地保留整段文本,尽可能连续删除或插入,而不是彼此交叉。
|
|||
|
|
2. 大部分人可能更习惯先看到原文本的删除,再看到目标文本的插入。
|
|||
|
|
|
|||
|
|
这两点其实也非常符合我们的直觉。反映到对编辑图的搜索上也非常直观:
|
|||
|
|
|
|||
|
|
1. 我们在探索路径时,如果碰到斜线一定要一路沿着斜线一路往下,直到不能继续为止,只有这样我们才能尽量多地保留连续的原始文本,这就是为什么要求 snake 终点不能停留在连续斜线中间的原因。
|
|||
|
|
2. 在考虑D-Path的时候,我们会优先从许多(D-1)-Path中,**挑选出一条终点的横坐标更大的路径来构建。这就意味着在做选择时倾向于选删除优先于插入的方式**。
|
|||
|
|
|
|||
|
|
现在你应该明白为什么要引入snake和line这样的概念了吧。核心就是斜线上的路径都是不需要产生编辑脚本长度的,因此我们可以选择在斜线上进行动态规划。
|
|||
|
|
|
|||
|
|
好了,最后我们来学习Myers的动态规划算法实现细节,理解了前面的概念,算法的思路就不是特别复杂了。
|
|||
|
|
|
|||
|
|
### 代码实现
|
|||
|
|
|
|||
|
|
我们用一个二维数dp来记录图上的搜索状态:
|
|||
|
|
|
|||
|
|
* dp的第一个维度代表着操作数,最大范围也就是我们最短编辑脚本的长度 m+n-2\*LC。
|
|||
|
|
* 第二个维度是k-Lines的行号,在操作数为d时,其取值范围为\[-d,d\],范围的左右边界分别代表了d次操作都是只插入不删除,或者只删除不插入。
|
|||
|
|
* dp本身的值记录为当前操作数及行号所对应的x坐标。
|
|||
|
|
|
|||
|
|
把之前的递推例子过程画到二维表格中大概如下图所示,横轴的数字代表着D-Path的D也就是操作数,纵轴的数字代表k-Lines的行号,树状图中每个节点展示的是网格中的二维坐标也都对应着某个编辑脚本的一部分:
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
| 0 1 2 3 4 5
|
|||
|
|
----+--------------------------------------
|
|||
|
|
|
|
|||
|
|
4 | 7,3
|
|||
|
|
| /
|
|||
|
|
3 | 5,2
|
|||
|
|
| /
|
|||
|
|
2 | [3,1] [7,5]
|
|||
|
|
| / \ / \
|
|||
|
|
1 | [1,0] [5,4] [7,6]
|
|||
|
|
| / \ \
|
|||
|
|
0 | [0,0] 2,2 5,5
|
|||
|
|
| \ \
|
|||
|
|
-1 | 0,1 4,5 5,6
|
|||
|
|
| \ / \
|
|||
|
|
-2 | 2,4 4,6
|
|||
|
|
| \
|
|||
|
|
-3 | 3,6
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
而方括号括起来的路径代表着我们最终选择的路径,也就是之前图里箭头表示的那条路径:
|
|||
|
|
|
|||
|
|
|
|||
|
|
我们从左到右、从下到上用两层循环依次更新二维表格。外层循环就是从左往右遍历图上的每一列,内层循环就是从下到上遍历树状图每一层的状态,也就是遍历每一条line。操作数为d时,我们从行号为-d开始以步长为2遍历,一直遍历到d。
|
|||
|
|
|
|||
|
|
整个树的结构是二叉的,奇数步时,必然处于奇数行号,偶数步时必然处于偶数行号。这是因为从k-Line的第k条线进行一步snake,只会有一次删除或者一次插入操作;对应到图上也就是经过一条横线或者一条竖线加若干条斜线,因而只能进入k+1行或者k-1行,所以每一个操作数对应行号的奇偶性是确定的,遍历的时候步长为2也就很好理解了。
|
|||
|
|
|
|||
|
|
所以总结一下就是,**行号为k、操作数为d的状态,只能从相邻的两行k-1或者k+1,通过横线或者竖线转移过来**。
|
|||
|
|
|
|||
|
|
写成状态转移方程就是 dp\[d\]\[k\] = max(dp\[d-1\]\[k-1\]+1,dp\[d-1\]\[k+1\])。从k-1行过来的必然走的是横线,所以状态也就是横坐标+1,从k行转移过来的走的是竖线,状态也就是横坐标会保持不变(动态规划状态不变)。这样,有多个选择的时候,我们会将状态更新为不同路径中最远的,也就是横坐标最大的一个。
|
|||
|
|
|
|||
|
|
思路很清晰,写成伪代码也非常简单啦。
|
|||
|
|
|
|||
|
|
如果在某次循环的时候找到了终点,就会停止循环,此时也找到了一种“简明”且最短的编辑脚本,直接return就行。由于操作数为D的状态数组的计算,仅依赖了操作数为D-1的一层状态数组,我们可以将状态维度压缩一下,采用一维数组记录状态。
|
|||
|
|
|
|||
|
|
```go
|
|||
|
|
V[1]←0
|
|||
|
|
For D ← 0 to MAX Do
|
|||
|
|
For k ← −D to D in steps of 2
|
|||
|
|
Do If k=−D or k≠D and V[k−1] < V[k+1] Then
|
|||
|
|
x ← V[k+1]
|
|||
|
|
Else
|
|||
|
|
x ← V[k−1]+1 y ← x−k
|
|||
|
|
While x < N and y < M and a[x+1] = b[y+1] Do
|
|||
|
|
(x,y) ← (x+1,y+1)
|
|||
|
|
V[k] ← x
|
|||
|
|
If x ≥ N and y ≥ M Then
|
|||
|
|
Length of an SES is D
|
|||
|
|
Stop
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
最后,我们来计算一下这个算法的时间复杂度,原论文花了许多篇幅在严谨的数学描述上,我们这里就写的简洁些,有兴趣的同学可以自己查阅论文进一步理解。
|
|||
|
|
|
|||
|
|
在内外两层的循环中,每一层循环都循环了D次,循环次数最多为总操作步数D\*D。循环体中,除了第8-10行的while,都是O(1)的复杂度。所以去掉8-10行之后,复杂度为O(D^2)。
|
|||
|
|
|
|||
|
|
8-10行的代码看似多加了一层复杂度不是常数的循环,但在做的事情就是沿着Line,在不耗费额外操作的时候,一路沿着snake往下拓展,所以整体复杂度加起来不可能超过搜索范围内的所有的长度斜线,而斜线的最大长度为min(M,N)。那么在循环范围内,8-10行的操作带来的总的时间复杂度不会超过O(M+N)。
|
|||
|
|
|
|||
|
|
所以算法的整体时间复杂度是O(D\*(M+N))。大部分情况下,D其实比M或者N要小许多,所以Myers算法在复杂度比O(M_M+N_N)要小很多。
|
|||
|
|
|
|||
|
|
## 总结
|
|||
|
|
|
|||
|
|
我们学习了一种高效求文本差分的方式 Myers 算法,基于动态规划的思想和编辑图的抽象,给出了一种复杂度很低又能求出可读性很高的编辑脚本的方法。这个算法被广泛使用在各种需要求文本差分的场景里,如Git中的git-diff、Android中的DiffUtil等。
|
|||
|
|
|
|||
|
|
其实,Myers算法并不是一个非常基础的算法。我会把这篇文章作为专栏的第一篇文章,不止因为这个算法确实非常有趣,能让你提前体验一下用算法来解决实际问题的思维乐趣;更是想告诉你,算法离我们的距离比你想的可能还要更近一些。
|
|||
|
|
|
|||
|
|
算法不只存在于各种高大上的基础设施或者艰深的论文里,而会出现在我们程序员日常开发工作中的每个角落,甚至生活的方方面面。只不过我们太习以为常,才忽略了这些算法。
|
|||
|
|
|
|||
|
|
所以,很期待在我们并肩探索算法的这段时间里,你能对真实世界中的算法有一个新的认知,并在欣赏它们的过程中提升自己,收获乐趣。
|
|||
|
|
|
|||
|
|
## 课后作业
|
|||
|
|
|
|||
|
|
留个小作业,前面有提到**最长公共子序列**的问题,不知道你会不会做呢?你可以试着实现一个朴素的基于动态规划的最长公共子序列算法,看看能不能基于这种实现改造出一个文本差分算法。
|
|||
|
|
|
|||
|
|
欢迎在留言区留下你的代码参与讨论。我为专栏开设的[GitHub仓库](https://github.com/wfnuser/Algorithms)也欢迎你来提issue和pr。
|
|||
|
|
|
|||
|
|
### 拓展阅读
|
|||
|
|
|
|||
|
|
感兴趣的话,你也可以自己尝试实现一下Myers算法。如果发现git-diff算出来的结果和你的结果略有不同,也不用担心,这很可能是因为git-diff优化了Myers算法的空间复杂度所导致的,这一点[原论文](http://www.xmailserver.org/diff2.pdf)里也有提到。
|
|||
|
|
|